1.A: Apéndice- Fundamentos matemáticos

1.A.1 Ángulos de un Triángulo

La ley de los cosenos relaciona los ángulos y longitudes de los lados del triángulo en la Figura\(\PageIndex{1}\) (a):

\[\begin{align}\label{eq:1}c^{2}&=a^{2}+b^{2}-2ab\cos(\gamma) \\ \label{eq:2} \cos(\alpha)=\frac{b^{2}+c^{2}-a^{2}}{2bc},\quad\cos(\beta)&=\frac{a^{2}+c^{2}-b^{2}}{2ac},\quad\cos(\gamma)=\frac{a^{2}+b^{2}-c^{2}}{2ab}\end{align} \]

Haciendo referencia al triángulo de ángulo recto en la Figura\(\PageIndex{1}\) (b):

\[\label{eq:3}\sin(x)=\frac{\text{opposite}}{\text{hypotenuse}},\quad\cos(x)=\frac{\text{adjacent}}{\text{hypotenuse}},\quad\tan(x)=\frac{\text{opposite}}{\text{adjacent}} \]

Figura\(\PageIndex{1}\): Triángulos: (a) triángulo con lados que tienen longitudes\(a, b,\) y\(c\), y ángulos\(\alpha, \beta,\) y\(\gamma\); y (b) triángulo en ángulo recto.

1.A.2 Identidades trigonométricas

\[\begin{align}\label{eq:4}\text{if }\sin(\theta)&=x\text{ then }\theta =\arcsin(x)\quad\text{if}\quad\cos(\theta)=x\text{ then }\theta =\arccos(x)\\ \label{eq:5}\text{if }\tan(\theta)&=x\text{ then }\theta =\arctan(x)\end{align} \]

\[\begin{align} \label{eq:6}\sin(-x)&=-\sin x &\cos(-x)&=\cos(x) &\tan(-x)&=-\tan x\\ \label{eq:7}\csc(-x)&=-\csc x &\sec(-x)&=\sec x &\cot(-x)&=-\cos x\end{align} \]

\[\label{eq:8}\cos(x)=\frac{1}{2}(e^{\jmath x}+e^{-\jmath x})\qquad \sin(x)=\frac{1}{2}\jmath(e^{-\jmath x}-e^{\jmath x}) \]

\[\begin{align}\label{eq:9}\sin x&=1/\csc x &\cos x&=1/\sec x &\tan x&=1/\cot x\\ \label{eq:10}\tan x&=\sin x/\cos x\end{align} \]

\[\label{eq:11}\sin^{2}x+\cos^{2}x=1\qquad 1+\tan^{2}x=\sec^{2}x\qquad 1+\cot^{2}x=\csc^{2}x \]

\[\begin{align}\label{eq:12}\sin\left(x-\frac{\pi}{2}\right)&=-\cos x &\cos\left(x-\frac{\pi}{2}\right)&=\sin x &\tan\left(x-\frac{\pi}{2}\right)&=-\cot x\\ \label{eq:13}\sin\left(x+\frac{\pi}{2}\right)&=\cos x &\cos\left(x+\frac{\pi}{2}\right)&=-\sin x &\tan\left(x+\frac{\pi}{2}\right)&=-\cot x\\ \label{eq:14}\sin\left(\frac{\pi}{2}-x\right)&=\cos x &\cos\left(\frac{\pi}{2}-x\right)&=\sin x &\tan\left(\frac{\pi}{2}-x\right)&=\cot x \\ \label{eq:15} \csc\left(x-\frac{\pi}{2}\right)&=-\sec x &\sec\left(x-\frac{\pi}{2}\right)&=\csc x &\cot\left(x-\frac{\pi}{2}\right)&=-\tan x \\ \label{eq:16} \csc\left(x+\frac{\pi}{2}\right)&=\sec x &\sec\left(x+\frac{\pi}{2}\right)&=-\csc x &\cot\left(x+\frac{\pi}{2}\right)&=-\tan x \\ \label{eq:17}\csc\left(\frac{\pi}{2}-x\right)&=\sec x &\sec\left(\frac{\pi}{2}-x\right)&=\csc x &\cot\left(\frac{\pi}{2}-x\right)&=\tan x\end{align} \]

\[\begin{align}\label{eq:18}\sin (2x)&=2\sin x\cos y &\cos(2x)&=\cos^{2}(x)-\sin^{2}(x)\\ \label{eq:19}\tan (2x)&=\frac{2\tan x}{1-\tan^{2}x} &\cot (2x)&=\frac{1}{2}[\cot (x)-\tan (x)]\end{align} \]

\[\label{eq:20}\sin^{2}x=\frac{1}{2}[1-\cos (2x)]\qquad \cos^{2}x=\frac{1}{2}[1+\cos (2x)]\qquad \tan^{2}x=\frac{1-\cos (2x)}{1+\cos (2x)} \]

\[\begin{align} \label{eq:21} \tan (x+y)&=\frac{\tan(x)+\tan(y)}{\tan(x)-\tan(y)} &\tan(x-y)&=\frac{\tan(x)-\tan(y)}{\tan(x)+\tan(y)} \\ \label{eq:22} \sin x+\sin y&=2\sin\left(\frac{x+y}{2}\right)\cos\left(\frac{x-y}{2}\right) &\sin x-\sin y &=2\cos\left(\frac{x+y}{2}\right)\sin\left(\frac{x-y}{2}\right) \\ \label{eq:23} \cos x+\cos y&=2\cos\left(\frac{x+y}{2}\right)\cos\left(\frac{x-y}{2}\right) &\cos x-\cos y&=-2\cos\left(\frac{x+y}{2}\right)\sin\left(\frac{x-y}{2}\right)\end{align} \]

\[\begin{align}\label{eq:24}\sin x\sin y&=\frac{1}{2}[\cos (x-y)-\cos (x+y)] &\sin x\cos y&=\frac{1}{2}[\sin (x+y) +\sin (x-y)] \\ \label{eq:25}\cos x\cos y&=\frac{1}{2}[\cos (x-y)+\cos (x+y)] &\cos x\sin y&=\frac{1}{2}[\sin (x+y)-\sin (x-y)]\end{align} \]

1.A.3 Derivados trigonométricos

\[\begin{align} \frac{d}{dx}\sin (x)&=\cos (x) &\frac{d}{dx}\cos (x)&=-\sin (x) &\frac{d}{dx}\tan (x)&=\sec^{2}(x) \nonumber\\ \frac{d}{dx}\csc (x)&=-\csc (x)\cot(x) &\frac{d}{dx}\sec (x)&=\sec (x)\tan (x) &\frac{d}{dx}\cot (x)&=-\csc^{2}(x)\nonumber\end{align} \nonumber \]

1.A.4 Números complejos y fasores

Un número complejo\(z\) es un par ordenado de dos números reales\(x\) y\(y\), y un número complejo tiene un significado especial cuando se trabaja en el dominio de la frecuencia. La forma rectangular del número complejo es\(z = x +\jmath y\), donde\(\jmath =\sqrt{-1}\) es un número imaginario. \(^{1}\)La forma polar del número complejo\(z = r\angle\varphi\) se relaciona directamente con la amplitud y fase de una cosinusoide. En la fase determinante, se hace referencia a una cosinusoide de la forma\(u(t) = r \cos (\omega t +\varphi)\), ya que ésta tiene un valor de\(r\) cuando la frecuencia del radián\(\omega = 0\) (es decir, a DC). La cosinusoide se muestra como la línea continua en la Figura\(\PageIndex{2}\) (a), donde\(r\) está la amplitud y\(\phi\) es la fase de la cosinusoide. La cosinusoide se puede presentar como la función de valor complejo

\[\label{eq:27}f(t)=ze^{\jmath\omega t},\qquad\text{where}\qquad z=re^{\jmath\phi} \]

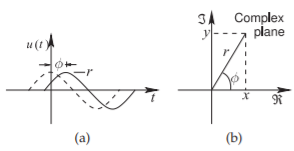
Figura\(\PageIndex{2}\): Representaciones de señal sinusoidal: (a) forma de onda referenciada a la cosinusoide zerofase mostrada como la forma de onda discontinua; y (b) representación como fasor en el plano complejo donde\(Re\) está la parte real y\(Im\) es la parte imaginaria.

se llama el fasor de\(u(t)\). El fasor contiene la amplitud y fase de la cosinusoide, y dada la frecuencia de la cosinusoide, se puede reconstruir la forma de onda original en el dominio del tiempo. La forma en el dominio del tiempo de la función compleja es

\[\label{eq:28} u(t)=\Re\left\{f(t)\right\} =\Re\left\{ze^{\jmath\omega t}\right\}=\Re\left\{re^{\jmath\phi}e^{\jmath\omega t}\right\}=\Re\left\{re^{[\jmath (\omega t+\phi)]}\right\}=r\cos(\omega t+\phi) \]

\(\Re\{\:\:\}\)indica que se toma la parte real de un número complejo, y de manera similar\(\Im\{\:\:\}\) indica que se toma la parte imaginaria de un número complejo. El número complejo se puede representar en forma rectangular o de fase de magnitud de modo que

\[\label{eq:29}z=x+\jmath y=r\angle\phi =re^{\jmath\phi}=r(\cos\phi +\jmath\sin\phi) \]

con la relación que se muestra en la Figura\(\PageIndex{2}\) (b). Obsérvese que en Ecuación\(\eqref{eq:29}\),\(\phi\) debe expresarse en radianes y en cualquier lugar se utilice en los cálculos. También

\[\label{eq:30}x=r\cos(\phi)\quad\text{and}\quad y=r\sin(\phi) \]

Cálculos básicos usando los números complejos

\[\label{eq:31}w=a+\jmath b=q\angle\theta\quad\text{and}\quad z=c+\jmath d=r\angle \phi \]

(con\(a,\: b,\: c,\: d ,\:\theta ,\:\phi ,\: r\), y\(q\) siendo números reales) son

• \(\jmath\cdot\jmath=\jmath^{2}=-1\)
• Adición:\(w + z = (a +\jmath b)+(c +\jmath d)=(a + c) + \jmath (b + d)\)
• Resta:\(w − z = (a + \jmath b) − (c + \jmath d)=(a − c) + \jmath (b − d)\)
• Multiplicación:\(w\cdot z = (a + \jmath b) \cdot (c +\jmath d)=(ac − bd) + \jmath (bc + ad)\)
• Magnitud:\(|w| = \sqrt{a^{2} + b^{2}} = q;\: |z| = \sqrt{c^{2} + d^{2}} = r\)
• Ángulo:\(\theta = \arctan(b/a) = \arccos(a/q) = \arcsin(b/q)\) (Es posible que se requiera corrección para obtener la fase en el cuadrante derecho. Esto requiere que se examinen los signos de a y b.)
• Multiplicación (alternativa):\(w\cdot z = qr\angle (\theta +\phi )\)
• División:\(w/z = \frac{a +\jmath b}{c +\jmath d} = \frac{(a + \jmath b)(c − \jmath d)}{(c + \jmath d)(c −\jmath d)} =\left(\frac{ac + bd }{c^{2} + d^{2}}\right) +\jmath\left(\frac{bc − ad}{c^{2} + d^{2}}\right)\)
• División (alternativa):\(w/z = q/r\angle (\theta − \phi)\)
• Raíz cuadrada:\(\sqrt{w} = \sqrt{q}\angle (\theta /2+m\pi ),\:\: m = 0, 1\) (es decir,\(\sqrt{w} = \sqrt{q}\angle (\theta /2)\) y\(\sqrt{q}\angle (\theta /2+\pi )\))
• \(n\)raíz th:\(\sqrt[n]{w} = \sqrt[n]{q}\angle \left(\theta /n + 2\pi\frac{m}{n}\right) ,\:\: m = 0, 1,\ldots (n − 1)\)
• Negativo:\(−w = −q\angle\theta = q\angle (\theta + \pi )\)
• Conjugado complejo:\(w^{\ast} = a −\jmath b = q\angle (−\theta )\)
• Magnitud cuadrada:\(|z|^{2} = z\cdot z^{\ast}\)
• Adición conjugada:\((w + z)^{\ast} = w^{\ast} + z^{\ast}\)
• Potencia conjugada:\((z^{n})^{\ast} = (z^{\ast})^{n}\)
• Multiplicación conjugada:\((wz)^{\ast} = w^{\ast}z^{\ast}\)
• División conjugada:\((w/z)^{\ast} = w^{\ast}/z^{\ast}\)
• Conjugada exponencial:\(\exp(z^{\ast}) = (\exp z)^{\ast}\)
• Logaritmo conjugado:\(\log(z^{\ast}) = (\log z)^{\ast}\)
• Conjugado conjugado:\((w^{\ast})^{\ast} = w\)
• Inversa compleja:\(z^{−1} = z^{\ast}/|z|^{2}\)
• Magnitud compleja:\(|z^{\ast}| = |z|\)

Ejemplo\(\PageIndex{1}\): Complex numbers

Considera los números complejos\(w = −0.5 −\jmath 1.6\) y\(z = 5 −\jmath 3\), y la forma de onda\(v(t)=2.3 \cos(2\pi 10t − 1.2)\).

• En forma polar,\(w = 1.676\angle (−1.874)\), donde\(1.874\) está en radianes; alternativamente\(w = 1.676\angle (−107.4)^{\circ}\).
• En forma polar,\(z = 5.831\angle (−0.54)\).
• \(2w = −1 − \jmath 3.2 = 3.353\angle (−1.874)\).
• \(z\cdot w = w\cdot z = w\cdot z = (1.676\cdot 5.831)\angle (−1.874−0.54) = 9.774\angle (−2.414) = −7.3−\jmath 6.5\).
• \(\sqrt{z} = 2.327 −\jmath 0.645\).
• Alternativamente\(\sqrt{z} = \sqrt{5.831}\angle (−0.54/2)=2.415\angle (−0.27)\).
• \(w/z = (1.676/5.831)\angle [−1.874 − (−0.54)] = 0.287\angle −1.333 = 0.068 −\jmath 6.5\).
• La frecuencia radián de\(v(t)\) es\(20\pi\text{ rads/s}\).
• La frecuencia de\(v(t)\) es\(10\text{ Hz}\).
• El fasor de\(v(t)\) es\(v = 2.3\angle (−1.2) = 2.3\angle (−68.755^{\circ})=0.833 −\jmath 2.144\).
• Si\(w\) es un fasor y su frecuencia es\(1\text{ GHz}\), la forma de onda equivalente a\(w\) es\(w(t) = 1.676 \cos(2\pi\cdot 10^{9}t − 1.874)\) y la fase es\(−1.874\) radianes o\(−107.35^{\circ}\) o\(252.65^{\circ}\).

1.A.5 Operadores vectoriales

Multiplicación vectorial

Hay dos tipos de operaciones que multiplican vectores. \(\mathbf{A},\: \mathbf{B},\)y\(\mathbf{C}\) son vectores con

\[\label{eq:32}\mathbf{A}=a_{i}\mathbf{i}+a_{j}\mathbf{j}+a_{k}\mathbf{k} \]

donde\(\mathbf{i},\: \mathbf{j},\) y\(\mathbf{k}\), son vectores ortogonales tales como los vectores unitarios del sistema de coordenadas cartesianas, es decir,\(\hat{\mathbf{x}},\: \hat{\mathbf{y}},\) y\(\hat{\mathbf{z}}\) en las\(z\) direcciones\(x,\: y,\) y, respectivamente

Producto Dot

\(\mathbf{A}\cdot\mathbf{B}\)se llama el producto punto, el producto escalar o el producto interno. Se lee como “un punto b”.

\(\mathbf{A}\cdot\mathbf{B}=a_{i}b_{i}+a_{j}b_{j}+\ldots +a_{k}b_{k}\)

Propiedad conmutativa:\(\mathbf{A}\cdot\mathbf{B} = \mathbf{B}\cdot\mathbf{A}\).

Propiedad distributiva:\(\mathbf{A}\cdot (\mathbf{B} +\mathbf{C}) = \mathbf{A}\cdot\mathbf{B} + \mathbf{A}\cdot\mathbf{C}\).

Propiedad bilineal (\(r\)es un escalar):\(\mathbf{A}\cdot (r\mathbf{B} + \mathbf{C}) = r(\mathbf{A}\cdot\mathbf{B})+(\mathbf{A}\cdot\mathbf{C})\).

Propiedad de multiplicación escalar (\(r\)y\(s\) son escalares):\((r\mathbf{A})\cdot (s\mathbf{B})=(rs)(\mathbf{A}\cdot\mathbf{B})\).

Propiedad ortogonal: Dos vectores distintos de cero\(\mathbf{A}\) y\(\mathbf{B}\) son ortogonales si y solo si\(\mathbf{A}\cdot\mathbf{B} = 0\).

Productos cruzados

\(\mathbf{A}\times\mathbf{B}\)se llama el producto cruzado. Se lee como “una cruz b”. Ahora los componentes vectoriales de\(\mathbf{A},\: \mathbf{B},\) y\(\mathbf{C}\) necesitan especificarse más estrechamente como vectores ortogonales, que normalmente tienen amplitud unitaria, que tienen la propiedad

\[\begin{align}\label{eq:33}\mathbf{i}\times\mathbf{j}&=\mathbf{k} &\mathbf{j}\times\mathbf{k}&=\mathbf{i} &\mathbf{k}\cdot\mathbf{i}&=\mathbf{j},\quad\text{and} &\mathbf{i}\times\mathbf{i}&=0=\mathbf{j}\times\mathbf{j}=\mathbf{k}\times\mathbf{k} \\ \label{eq:34} \mathbf{j}\times\mathbf{i}&=-\mathbf{k} &\mathbf{k}\times\mathbf{j}&=-\mathbf{i} &\mathbf{i}\times\mathbf{k}&=-\mathbf{j}\end{align} \]

Los vectores unitarios del sistema de coordenadas cartesianas tienen esta propiedad con\(\mathbf{i},\: \mathbf{j},\) y\(\mathbf{k}\), correspondiente a los vectores unitarios\(\hat{\mathbf{x}}\)\(\hat{\mathbf{y}}\), y\(\hat{\mathbf{z}}\) en las\(z\) direcciones\(x,\: y,\) y, respectivamente.

\[\begin{align}\mathbf{a}\times\mathbf{b}&=(a_{i}\mathbf{i}+a_{j}\mathbf{j}+a_{k}\mathbf{k})\times (b_{i}\mathbf{i}+b_{j}\mathbf{j}+b_{k}\mathbf{k})\nonumber \\ &=a_{i}b_{i}\mathbf{i}\times\mathbf{i}+a_{i}b_{j}\mathbf{i}\times\mathbf{j}+a_{i}b_{k}\mathbf{i}\times\mathbf{k}+a_{j}b_{i}\mathbf{j}\times\mathbf{i}+a_{j}b_{j}\mathbf{j}\times\mathbf{j}+a_{j}b_{k}\mathbf{j}\times\mathbf{k} +\nonumber \\ &\quad a_{k}b_{i}\mathbf{k}\times\mathbf{i}+a_{k}b_{j}\mathbf{k}\times\mathbf{j}+a_{k}b_{k}\mathbf{k}\times\mathbf{k}\nonumber \\ \label{eq:35} &=(a_{j}b_{k}-a_{k}b_{j})\mathbf{i}+(a_{k}b_{i}-a_{i}b_{k})\mathbf{j}+(a_{i}b_{j}-a_{j}b_{i})\mathbf{k}\end{align} \]

Propiedad anticonmutativa:\(\mathbf{A}\times\mathbf{B} = −\mathbf{B}\times\mathbf{A}\).

Propiedad distributiva:\(\mathbf{A}\times (\mathbf{B} +\mathbf{C}) = \mathbf{A}\times \mathbf{B} + \mathbf{A}\times\mathbf{C}\).

Propiedad bilineal (\(r\)es un escalar):\(\mathbf{A}\times (r\mathbf{B} + \mathbf{C}) = r(\mathbf{A}\times \mathbf{B})+(\mathbf{A}\times \mathbf{C})\).

Propiedad de multiplicación escalar (\(r\)y\(s\) son escalares):\((r\mathbf{A})\times (s\mathbf{B})=(rs)(\mathbf{A}\times\mathbf{B})\).

La fórmula de Lagrange

\(\mathbf{A}\times (\mathbf{B}\times\mathbf{C})=\mathbf{B}(\mathbf{B}\cdot\mathbf{C})-\mathbf{C}(\mathbf{A}\cdot\mathbf{B})\)

Del (\(\nabla\)) Operador de vectores

Operaciones en sistemas de coordenadas cartesianas, cilíndricas y esféricas

Esta sección define el del, o la nabla\(\nabla\), un operador de cálculo que opera sobre cantidades vectoriales y también en un escalar para crear un vector. Se presentan los diferentes operadores en los sistemas de coordenadas cartesianas (rectangulares), esféricas y cilíndricas. Aquí un escalar se denota por\(f\) y un vector por\(\mathbf{F}\):

• grad,\(\nabla\), es el gradiente de un escalar con dirección. \(\nabla f\)se lee como “grad f.”
• div,\(\nabla\), es una medida de cómo se está extendiendo un vector desde un punto. \(\nabla\cdot\mathbf{F}\)se lee como “div F.”
• curl,\(\nabla\times\), es una medida de la rotación de un vector. \(\nabla\times\mathbf{F}\)se lee como “rizo F.”

Coordenadas cartesianas (rectangulares)\((x, y, z)\):

\(\hat{x}\)es el vector unitario en la\(x\) dirección y\(F_{x}\) es el componente del campo en la\(x\) dirección. De manera similar para los demás componentes.

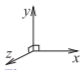
Figura\(\PageIndex{3}\)

\[\begin{align}\label{eq:36}\mathbf{F}&=F_{x}\hat{x}+F_{y}\hat{y}+F_{z}\hat{z} \\ \label{eq:37}\text{grad}\quad\nabla f&=\frac{\partial f}{\partial x}\hat{\mathbf{x}}+\frac{\partial f}{\partial y}\hat{\mathbf{y}}+\frac{\partial f}{\partial z}\hat{\mathbf{z}} \\ \label{eq:38}\text{div}\quad\nabla\cdot\mathbf{F}&=\frac{\partial F_{x}}{\partial x}+\frac{\partial F_{y}}{\partial y}+\frac{\partial F_{z}}{\partial z} \\ \label{eq:39}\text{curl}\quad\nabla\times\mathbf{F}&=\left(\frac{\partial F_{z}}{\partial y}-\frac{\partial F_{y}}{\partial z}\right)\hat{\mathbf{z}}+\left(\frac{\partial F_{x}}{\partial z}-\frac{\partial F_{z}}{\partial x}\right)\hat{\mathbf{y}}+\left(\frac{\partial F_{y}}{\partial x}-\frac{\partial F_{x}}{\partial y}\right)\hat{\mathbf{z}} \\ \label{eq:40}\nabla^{2}\mathbf{F}&=\frac{\partial^{2}\mathbf{F}}{\partial x^{2}}+\frac{\partial^{2}\mathbf{F}}{\partial y^{2}}+\frac{\partial^{2}\mathbf{F}}{\partial z^{2}} \\ \label{eq:41}\text{differential length, }d\ell &=dx\:\hat{\mathbf{x}}+dy\:\hat{\mathbf{y}}+dz\:\hat{\mathbf{z}} \\ \label{eq:42} \text{differential normal area, }d\mathbf{s}&=dy\:dz\:\hat{\mathbf{x}}+dx\:dz\:\hat{\mathbf{y}}+dx\:dy\:\hat{\mathbf{z}} \\ \label{eq:43} \text{differential volume, }dv&=dx\:dy\:dz\end{align} \]

Coordenadas cilíndricas\((\rho, \phi, z)\):

Las coordenadas cilíndricas son\(\rho\)\(\phi\) para radio, ángulo y\(z\) altura. Estos están relacionados con las coordenadas cartesianas por

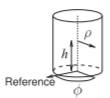
Figura\(\PageIndex{4}\)

\[\begin{align} \label{eq:44} x&=\rho\cos\phi,&y&=\rho\sin\phi, \quad z=z \\ \label{eq:45}\rho&=\sqrt{x^{2}+y^{2}} &\phi &=\text{atan}2(y,x), \quad z=z \\ \label{eq:46} &\text{vector} &\mathbf{F}&=F_{\rho}\hat{\mathbf{ρ}}+F_{\phi}\hat{\mathbf{ϕ}}+F_{z}\hat{\mathbf{z}} \\ \label{eq:47} &\text{grad} &\nabla f&=\frac{\partial f}{\partial\rho}\hat{\mathbf{ρ}} +\frac{1}{\rho}\frac{\partial f}{\partial\phi}\hat{\mathbf{ϕ}}+\frac{\partial f}{\partial z}\hat{\mathbf{z}} \\ \label{eq:48} &\text{div} &\nabla\cdot\mathbf{F}&=\frac{1}{\rho}\frac{\partial_{\rho}F_{\rho}}{\partial\rho} +\frac{1}{\rho}\frac{\partial F_{\phi}}{\partial\phi}+\frac{\partial F_{z}}{\partial z} \\ \label{eq:49} &\text{curl}&\nabla\times\mathbf{F}&=\left(\frac{1}{\rho}\frac{\partial F_{z}}{\partial\phi}-\frac{\partial F_{\phi}}{\partial z}\right)\hat{\mathbf{ρ}}+\left(\frac{\partial F_{\rho}}{\partial z}-\frac{\partial F_{z}}{\partial\rho}\right)\hat{\mathbf{ϕ}}+\frac{1}{\rho}\left(\frac{\partial (\rho F_{\phi})}{\partial\rho}-\frac{\partial F_{\rho}}{\partial\phi}\right)\hat{\mathbf{z}} \end{align} \]

\[\begin{align}\label{eq:50}\text{ differential length, }d\ell&=d\rho\hat{\mathbf{ρ}}+\rho \:d\phi \hat{\mathbf{ϕ}}+dz\:\hat{\mathbf{z}} \\ \label{eq:51}\text{differential normal area, }d\mathbf{s}&=\rho\: d\phi\: dz\hat{\mathbf{ρ}}+d\rho \:dz\:\hat{\mathbf{ϕ}}+\rho\:d\rho \:d\phi \hat{\mathbf{z}} \\ \label{eq:52}\text{differental volume, }dv&=\rho\: d\rho \:d\phi \:dz\end{align} \]

Coordenadas esféricas\((\rho, \theta, \phi)\):

Las coordenadas esféricas son\(\rho\) para el radio,\(\theta\) para el ángulo de la proyección horizontal y\(\phi\) para el ángulo de elevación. Estos están relacionados con las coordenadas cartesianas por

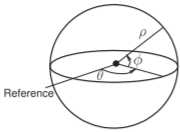
Figura\(\PageIndex{5}\)

\[\begin{align}\label{eq:53} x& =r\sin \theta \cos \phi , & y & =r\sin \theta \sin \phi, \quad z=r\cos \theta \\ \label{eq:54} r&=\sqrt{x^{2}+y^{2}+z^{2}} &\theta&=\arccos(z/r),\quad \phi=\text{atan}2(y, x) \\ \label{eq:55} &\text{vector} &\mathbf{F}&=F_{r}\hat{\mathbf{r}}+F_{\theta}\hat{\mathbf{θ}}+F_{\phi}\hat{\mathbf{ϕ}} \\ \label{eq:56} &\text{grad} &\nabla f&=\frac{\partial f}{\partial r}\hat{\mathbf{r}}+\frac{1}{r}\frac{\partial f}{\partial \theta}\hat{\mathbf{θ}}+\frac{1}{r\sin\theta}\frac{\partial f}{\partial\phi}\hat{\mathbf{ϕ}} \\ \label{eq:57}&\text{div}&\nabla\cdot\mathbf{F}&=\frac{1}{r^{2}}\frac{\partial (r^{2}F_{r})}{\partial r}+\frac{1}{r\sin\theta}\frac{\partial (F_{\theta}\sin\theta)}{\partial\theta}+\frac{1}{r\sin\theta}\frac{\partial F_{\phi}}{\partial\phi} \\ &\text{curl}&\nabla\times\mathbf{F}&=\frac{1}{r\sin\theta}\left(\frac{\partial(F_{\phi}\sin\theta)}{\partial\theta}-\frac{\partial F_{\theta}}{\partial\phi}\right)\hat{\mathbf{r}} \\ \label{eq:58}&&&\quad +\frac{1}{r}\left(\frac{1}{\sin\theta}\frac{\partial F_{r}}{\partial\theta}-\frac{\partial (rF_{\phi})}{\partial r}\right)\hat{\mathbf{θ}} +\frac{1}{r}\left(\frac{\partial (rF_{\theta})}{\partial r}-\frac{\partial F_{r}}{\partial\theta}\right)\hat{\mathbf{ϕ}} \end{align} \]

\[\begin{align}\label{eq:59}\text{differential length }d\ell &=dr\:\hat{\mathbf{r}}+r\:d\theta\:\hat{\mathbf{θ}} +r\sin\theta\:d\phi\:\hat{\mathbf{ϕ}} \\ \label{eq:60}\text{differential area }d\mathbf{s}&=r^{2}\sin\theta\:d\theta\:d\phi\:\hat{\mathbf{r}}+r\sin\theta\:dr\:d\phi\:\hat{\mathbf{θ}} +r\:dr\:d\theta\:\hat{\mathbf{ϕ}} \\ \label{eq:61}\text{differential volume }dv&=r^{2}\sin\theta\:dr\:d\theta\:d\phi\end{align} \]

Identidades

Identidades para el operador del\(\nabla\),,:

\[\begin{align}\label{eq:62}\text{div grad }f&=\nabla\cdot (\nabla f)=\nabla^{2}f=\Delta f\text{(Laplacian)} \\ \label{eq:63}\Delta (fg)&=f\Delta g+2\nabla f\cdot\nabla g+g\Delta f \\ \label{eq:64} \text{curl grad }f&=\nabla\times (\nabla f)=0 \\ \label{eq:65}\text{div curl }\mathbf{F}&=\nabla\cdot (\nabla\times\mathbf{F})=0 \\ \label{eq:66}\text{curl curl }\mathbf{F}&=\nabla\times (\nabla\times\mathbf{F})=\nabla (\nabla\cdot F)-\nabla^{2}F \\ \label{eq:67}\mathbf{A}\times (\mathbf{B}\times\mathbf{C})&=\mathbf{B}(\mathbf{A}\cdot\mathbf{C})-\mathbf{C}(\mathbf{A}\cdot\mathbf{B})\end{align} \]

1.A.6 Funciones hiperbólicas y números complejos

\[\begin{align}\label{eq:68}\cosh (x)&=\frac{1}{2}(e^{x}+e^{-x})=\cos (\jmath x) \\ \label{eq:69}\cosh (\jmath x)&=\frac{1}{2}(e^{\jmath x}+e^{-\jmath x})=\cos (x) \\ \label{eq:70}\cosh (-x)&=\cosh (x)\end{align} \]

\[\begin{align}\label{eq:71}\sinh(x)&=\frac{1}{2}(e^{x}-e^{-x})=-\jmath\sin(\jmath x) \\ \label{eq:72}\sinh (\jmath x)&=\frac{1}{2}(e^{\jmath x}-e^{-\jmath x})=\jmath\sin (x) \\ \label{eq:73}\sinh(-x)&=-\sinh (x)\end{align} \]

\[\label{eq:74}\cosh^{2}(x)-\sinh^{2}(x)=1 \]

\[\begin{align}\label{eq:75}\tanh(x)&=\sinh(x)/\cosh(x) \\ \label{eq:76}\tanh(x)&=-\jmath\tan(\jmath x) \\ \label{eq:77}\tanh(\jmath x)&=\jmath\tan(x) \\ \label{eq:78} \tanh(-x)&=-\tanh(x)\end{align} \]

\[\begin{align}\label{eq:79}\sin(\jmath x)&=\jmath\sinh(x) \\ \label{eq:80}\cos(\jmath x)&=\cosh (x) \\ \label{eq:81}\tan(\jmath x)&=\jmath\tanh(x)\end{align} \]

\[\begin{align}\label{eq:82}e^{x}&=\cosh(x)+\sinh(x) &e^{-x}&=\cosh(x)-\sinh(x) \\ \label{eq:83}e^{\jmath x}&=\cos(x)+\jmath\sin(x) &e^{-\jmath x}&=\cos(x)-\jmath\sin(x)\end{align} \]

\[\begin{align}\label{eq:84}\sin(x+\jmath y)&=\sin(x)\cosh(y)+\jmath\cos(x)\sinh(y) \\ \label{eq:85}\cos(x+\jmath y)&=\cos(x)\cosh(y)-\jmath\sin(x)\sinh(y)\end{align} \]

\[\label{eq:86}e^{\gamma}=e^{(\alpha +\jmath\beta)}=e^{\alpha}e^{\jmath\beta},\text{ where }\gamma =\alpha +\jmath\beta \]

\[\label{eq:87}\cot(x)=\frac{1}{2}[\cot (x/2)-\tan(x/2)] \]

1.A.7 Volúmenes y áreas

	Círculo	Esfera	Cilindro	Cono
	\(r=\)radio	\(r=\)radio	\(r=\)radio \(h=\)altura	\(r=\)radio de la base \(h=\)altura
Área	\(\pi r^{2}\)	\(4\pi r^{2}\)	\(2\pi rh\)(cilindro) \(2\pi r^{2}\)(base y parte superior)
Volumen		\(4\pi r^{3}/3\)	\(\pi r^{2}h\)	\(\pi r^{2}h/3\)

Mesa\(\PageIndex{1}\)

Expansiones de la serie 1.A.8

Raíz cuadrada:

\[\begin{align} \sqrt{1+x}&=\sum_{n=0}^{\infty}\frac{(-1)^{n}(2n)!}{(1-2n)(n!)^{2}(4^{n})}x^{n}\nonumber \\ \label{eq:88}&=1+\frac{1}{2}x-\frac{1}{8}x^{2}+\frac{1}{16}x^{3}-\frac{5}{128}x^{4}+\ldots \text{ for }-1< x\leq 1\end{align} \]

Función exponencial (el número natural e elevado a una potencia):

\[\label{eq:89}e^{x}=\sum_{n=0}^{\infty}\frac{x^{n}}{n!}=1+x+\frac{x^{2}}{2!}+\frac{x^{3}}{3!}+\ldots\text{ for all }x \]

Logaritmo natural:

\[\begin{align} \label{eq:90}\ln(1-x)&=-\sum_{n=1}^{\infty}\frac{x^{n}}{n}\text{ for }-1\leq x<1 \\ \label{eq:91}\ln(1+x)&=\sum_{n=1}^{\infty}(-1)^{n+1}\frac{x^{n}}{n}\text{ for }-1<x\leq 1\end{align} \]

Serie binomial:

\[\label{eq:92}(1+x)^{\alpha}=\sum_{n=0}^{\infty}\left(\begin{array}{c}{\alpha}\\{n}\end{array}\right)x^{n}\quad\text{ for all }|x|<1\text{ and all complex }\alpha \]

donde\(n\) es un entero y el coeficiente binomial es

\[\label{eq:93} \left(\begin{array}{c}{\alpha}\\{n}\end{array}\right)=\prod_{k=1}^{n}\frac{\alpha -k+1}{k}=\frac{\alpha (\alpha -1)\ldots (\alpha -n+1}{n!} \]

Si\(\alpha\) se reemplaza por un entero\(N\) el coeficiente binomial es

\[\label{eq:94} \left(\begin{array}{c}{N}\\{n}\end{array}\right)=\frac{N!}{(N-n)!n!} \]

Serie geométrica infinita:

\[\begin{align}\label{eq:95}\frac{1}{1-x}&=\sum_{n=0}^{\infty}x^{n}\quad\text{for }|x|<1 \\ \label{eq:96}\frac{x}{(1-x)^{2}}&=\sum_{n=1}^{\infty}nx^{n}\quad\text{for }|x|<1 \\ \label{eq:97}\frac{1}{(1-x)^{2}}&=\sum_{n=1}^{\infty}nx^{n-1}\quad\text{for }|x|<1\end{align} \]

1.A.9 Expansiones de la Serie Trigonométrica

\[\begin{align}\label{eq:98} \sin x&=\sum_{n=0}^{\infty}\frac{(-1)^{n}}{(2n+1)!}x^{2n+1}=x-\frac{x^{3}}{3!}+\frac{x^{5}}{5!}-\cdots\text{ for all }x \\ \label{eq:99} \cos x&=\sum_{n=0}^{\infty}\frac{(-1)^{n}}{(2n)!}x^{2n}=1-\frac{x^{2}}{2!}+\frac{x^{4}}{4!}-\cdots\text{ for all }x \\ \label{eq:100}\tan x&=x+\frac{x^{3}}{3}+\frac{2x^{5}}{15}+\cdots\text{ for }|x|<\frac{\pi}{2} \\ \label{eq:101}\sinh x&=\sum_{n=0}^{\infty}\frac{x^{2n+1}}{(2n+1)!}=x+\frac{x^{3}}{3!}+\frac{x^{5}}{5!}+\cdots\text{ for all }x \\ \label{eq:102} \cosh x&=\sum_{n=0}^{\infty}\frac{x^{2n}}{(2n)!}=1+\frac{x^{2}}{2!}+\frac{x^{4}}{4!}+\cdots\text{ for all }x \\ \label{eq:103}\tanh x&=\sum_{n=1}^{\infty}\frac{B_{2n}4^{n}(4^{n}-1)}{(2n)!}x^{2n-1}=x-\frac{1}{3}x^{3}+\frac{2}{15}x^{5}-\frac{17}{315}x^{7}+\cdots\text{ for }|x|<\frac{\pi}{2} \\ \label{eq:104}\text{arsinh}(x)&=\sum_{n=0}^{\infty}\frac{(-1)^{n}(2n)!}{4^{n}(n!)^{2}(2n+1)}x^{2n+1}\text{ for }|x|\leq 1 \\ \label{eq:105} \text{artanh}(x)&=\sum_{n=0}^{\infty}\frac{x^{2n+1}}{2n+1}\text{ for }|x|<1\end{align} \]

1.A.10 Polinomios especiales

Varios polinomios tienen propiedades especiales de uso en el diseño de filtros y redes coincidentes. Sus argumentos se ponen en términos de frecuencia y una función de transferencia de un puerto de dos puertos se expresa en términos sobre uno de los polinomios especiales o su inverso.

Polinomio Butterworth

Los polinomios Butterworth tienen la forma general

\[\label{eq:106}B_{n}(x)=\left\{\begin{array}{ll}{\prod_{k=1}^{n/2}\left\{x^{2}-2x\cos\left[\frac{(2k+n-1)\pi}{2n}\right]+1\right\}}&{\text{for }n\text{ even}}\\{(x+1)\prod_{k=1}^{(n-1)/2}\left\{x^{2}-2x\cos\left[\frac{(2k+n-1)\pi}{2n}\right]+1\right\}}&{\text{for }n\text{ odd}}\end{array}\right. \]

Estos por supuesto no parecen polinomios pero sus expansiones lo son, ver Tabla\(\PageIndex{2}\).

Polinomio Chebyshev

El\(n\) polinomio Chebyshev de primer tipo\(T_{n}(x)\), (a menudo llamado polinomio Chebyshev) tiene la propiedad especial de que\(−1\leq x\leq 1\) es el valor absoluto máximo de\(T_{n}(x)\) for\(1\). Esto se puede apreciar en la figura de la derecha donde se trazan los primeros cuatro polinomios de Tchebyshev.

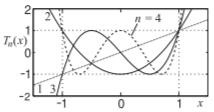
Figura\(\PageIndex{6}\)

Cuando\(x\) es frecuencia esto significa que la respuesta de frecuencia en un ancho de banda tiene ondas iguales a través de la banda de paso y fuera (tanto por encima como por debajo) el valor de diverge\(T_{n}(x)\) rápidamente (la magnitud se vuelve monótonamente mayor). Para un filtro o red coincidente el coeficiente de reflexión se expresa en términos de\(T_{n}(x)\) y así los faldones de la respuesta de transmisión son pronunciados. La normalización\(x\) y escalado de los polinomios de Chebyshev se utiliza para escalar la respuesta en frecuencia y amplitud. El polinomio de Chebyshev se obtiene usando la fórmula de recursión

\[\label{eq:107}T_{n}(x)=2xT_{n-1}-T_{n-2}(x)\quad\text{with}\quad T_{1}(x)=x\quad\text{and}\quad T_{2}(x)=2x^{2}-1 \]

Por ejemplo, con\(n = 3\),

\[\label{eq:108}T_{3}(x)=2xT_{3-1}(x)-T_{3-2}(x)=2x(2x^{2}-1)-x=4x^{3}-2x-x=4x^{3}-3x \]

\(n\)	Polinomio Butterworth\(B_{n}(x)\)
\ (n\) ">\(1\)	\ (B_ {n} (x)\)” class="lt-eng-41011">\(x+1\)
\ (n\) ">\(2\)	\ (B_ {n} (x)\)” class="lt-eng-41011">\(x^{2}+1.4142x+1\)
\ (n\) ">\(3\)	\ (B_ {n} (x)\)” class="lt-eng-41011">\((x+1)(x^{2}+x+1\)
\ (n\) ">\(4\)	\ (B_ {n} (x)\)” class="lt-eng-41011">\((x^{2} + 0.7564x + 1)(x^{2} + 1.8478x + 1)\)
\ (n\) ">\(5\)	\ (B_ {n} (x)\)” class="lt-eng-41011">\((x + 1)(x^{2} + 0.1680x + 1)(x^{2} + 1.6180x + 1)\)
\ (n\) ">\(6\)	\ (B_ {n} (x)\)” class="lt-eng-41011">\((x^{2} + 0.5176x + 1)(x^{2} + 1.4142x + 1)(x^{2} + 1.9319x + 1)\)
\ (n\) ">\(7\)	\ (B_ {n} (x)\)” class="lt-eng-41011">\((x + 1)(x^{2} + 0.4450x + 1)(x^{2} + 1.2470x + 1)(x^{2} + 1.8019x + 1)\)
\ (n\) ">\(8\)	\ (B_ {n} (x)\)” class="lt-eng-41011">\((x^{2} + 0.3902x + 1)(x^{2} + 1.1111x + 1)(x^{2} + 1.6629x + 1)(x^{2} + 1.9616x + 1)\)

Cuadro\(\PageIndex{2}\): Polinomios Butterworth.

Varias expansiones útiles de polinomios de Chebyshev se utilizan en ingeniería de microondas para relacionar la respuesta de frecuencia de una función o circuito con la característica de Chebyshev. Generalmente la frecuencia se refiere a la longitud eléctrica\(\theta\) (que para una línea de transmisión\(\theta\) es proporcional a la frecuencia). Algunas de las expansiones más útiles utilizadas en el texto siguen:

\[\label{eq:109}T_{n}(\cos\theta)=\cos(n\theta) \]

y tenga en cuenta que\(\theta = \pi /2, \cos(n\theta )=0\) cuando es impar y\(\cos(n\theta ) = \pm 1\) cuando es par. De esta identidad se derivan dos identidades más útiles:

\[\label{eq:110}T_{n}(x) = \cos\left( n \cos^{−1} x\right)\quad\text{for}\quad |x| ≤ 1,\quad\text{and}\quad T_{n}(x) = \cosh\left( n \cosh^{−1} x\right)\quad\text{for}\quad |x| ≥ 1 \]

A menudo\(\cos\theta/ \cos\theta_{m}\) se usa un argumento normalizado para definir una banda de paso como entre\(\theta_{m}\) y\((\pi −\theta_{m})\). Es decir que podemos relacionar la respuesta de Chebyshev con la frecuencia y definir un ancho de banda de frecuencia. Entonces una útil expansión polinómica de Chebyshev es

\[\label{eq:111} T_{n} (\cos\theta /\cos\theta_{m}) = T_{n}(\sec\theta_{m}\cos\theta) = \cos\left\{ n\left[ \cos^{−1} (\cos\theta/\cos\theta_{m})\right]\right\} \]

De la Sección 1.A.2 señalar que\(\cos^{2}\theta = \frac{1}{2} [1 + \cos(2\theta)]\),\(\cos\theta \cos(n\theta) = \frac{1}{2} \cos[(n + 1)\theta] \cos[(n − 1)\theta]\), y\(\sec(\theta_{m})=1/ \cos\theta_{m}\). Entonces (después de ingeniosa manipulación) Ecuación\(\eqref{eq:107}\) se convierte

\[\begin{align}T_{1}(\cos\theta /\cos\theta_{m})&=\sec\theta_{m}\cos\theta \nonumber \\ T_{2}(\cos\theta/\cos\theta_{m})&=\sec^{2}\theta_{m}[\cos(2\theta)+1]-1=\sec^{2}\theta_{m}\cos(2\theta)+(\sec^{2}\theta_{m}-1) \nonumber \\ T_{3}(\cos\theta/\cos\theta_{m})&=\sec^{3}\theta_{m}[\cos(3\theta)+3\cos\theta]-3\sec\theta_{m}\cos\theta \nonumber \\ &=\sec^{3}\theta_{m}\cos(3\theta)+3(\sec^{3}\theta_{m}-\sec\theta_{m})\cos\theta\nonumber \\ T_{4}(\cos\theta/\cos\theta_{m})&=\sec^{4}\theta_{m}[\cos(4\theta)+4\cos(2\theta)+3]-4\sec^{2}\theta_{m}[\cos(2\theta)+1]+1\nonumber \\ &=\sec^{4}\theta_{m}\cos(4\theta)+4(\sec^{4}-\sec^{2}\theta_{m})\cos(2\theta)+(3\sec^{4}\theta_{m}-4\sec^{2}\theta_{m}+1)\nonumber \\ K_{5}(\cos\theta/\cos\theta_{m})&=\sec^{5}\theta_{m}[\cos(5\theta)+5\cos(3\theta)+7\cos\theta]-\sec^{3}\theta_{m}[5\cos(3\theta)+11\cos\theta] \nonumber \\ &\quad +4\sec\theta_{m}\cos\theta\nonumber \\ &=\sec^{5}\theta_{m}\cos(5\theta)+5(\sec^{5}\theta_{m}-\sec^{3}\theta_{m})\cos(3\theta)\nonumber \\ \label{eq:112}&\quad +(7\sec^{5}\theta_{m}-11\sec^{3}\theta_{m}+4\sec\theta_{m})\cos\theta\end{align} \]

1.A.11 Operaciones matriciales

\(\mathbf{A}\)\(\mathbf{B}\), y\(\mathbf{C}\) son matrices cuadradas y V es un vector.

Determinante:

\[\label{eq:113}|\mathbf{A}|=\det (\mathbf{A}) \]

Transponer:

\[\begin{align}\label{eq:114}(\mathbf{ABC})^{\text{T}}&=\mathbf{C}^{\text{T}}\mathbf{B}^{\text{T}}\mathbf{A}^{\text{T}} \\ \label{eq:115}(\mathbf{ABC}^{\text{T}})^{\text{T}}&=\mathbf{CB}^{\text{T}}\mathbf{A}^{\text{T}}\end{align} \]

Inversa:

\[\begin{align}\label{eq:116}(\mathbf{ABC})^{-1}&=\mathbf{C}^{-1}\mathbf{B}^{-1}\mathbf{A}^{-1} \\ \label{eq:117}(\mathbf{ABC}^{-1})^{-1}&=(\mathbf{C}^{-1})^{-1}\mathbf{B}^{-1}\mathbf{A}^{-1}=\mathbf{CB}^{-1}\mathbf{A}^{-1} \\ \label{eq:118}\mathbf{AA}^{-1}&=\mathbf{A}^{-1}\mathbf{A}=\mathbf{I}=\mathbf{1}\end{align} \]

Matrices cuadradas de dos filas y vectores

\[\label{eq:119}\mathbf{A} = \left[\begin{array}{cc}{a_{11}}&{a_{12}}\\{a_{21}}&{a_{22}}\end{array}\right]\quad\mathbf{B}=\left[\begin{array}{cc}{b_{11}}&{b_{12}}\\{b_{21}}&{b_{22}}\end{array}\right]\quad\mathbf{V}=\left[\begin{array}{c}{v_{1}}\\{v_{2}}\end{array}\right] \]

Multiplicación:

\[\begin{align}\label{eq:120}\mathbf{AV}&=\left[\begin{array}{cc}{a_{11}}&{a_{12}}\\{a_{21}}&{a_{22}}\end{array}\right]\left[\begin{array}{c}{v_{1}}\\{v_{2}}\end{array}\right] =\left[\begin{array}{c}{(a_{11}v_{1}+a_{12}v_{2})}\\{(a_{21}v_{1}+a_{22}v_{2})}\end{array}\right] \\ \label{eq:121}\mathbf{AB}&=\left[\begin{array}{cc}{a_{11}}&{a_{12}}\\{a_{21}}&{a_{22}}\end{array}\right]\left[\begin{array}{cc}{b_{11}}&{b_{12}}\\{b_{21}}&{b_{22}}\end{array}\right]=\left[\begin{array}{cc}{(a_{11}b_{11}+a_{12}b_{21})}&{(a_{11}b_{21}+a_{12}b_{22})}\\{(a_{21}b_{11}+a_{22}b_{21})}&{(a_{21}b_{12}+a_{22}b_{22})}\end{array}\right]\end{align} \]

Determinante:

\[\label{eq:122}|\mathbf{A}|=\det(\mathbf{A})=\det\left(\left[\begin{array}{cc}{a}&{b}\\{c}&{d}\end{array}\right]\right)=\frac{1}{ad-bc} \]

Transponer:

\[\label{eq:123}\mathbf{A}^{\text{T}}=\left[\begin{array}{cc}{a_{11}}&{a_{12}} \\ {a_{21}}&{a_{22}}\end{array}\right]^{\text{T}}=\left[\begin{array}{cc}{a_{11}}&{a_{21}} \\ {a_{12}} &{a_{22}}\end{array}\right] \]

Inversa:

\[\label{eq:124}\mathbf{A}^{-1}=\left[\begin{array}{cc}{a}&{b}\\{c}&{d}\end{array}\right]^{-1} =\frac{1}{|\mathbf{A}|}\left[\begin{array}{cc}{d}&{-b} \\ {-c}&{d}\end{array}\right]=\frac{1}{ad-bc}\left[\begin{array}{cc}{d}&{-b} \\ {-c}&{d}\end{array}\right] \]

1.A.12 Interpolación

Interpolación lineal

La interpolación lineal se puede utilizar para extraer datos de tablas. En la siguiente tabla hay dos puntos conocidos,\((x_{0}, y_{0})\) y\((x_{1}, y_{1})\), y el interpolante lineal es la línea recta entre ellos. El punto desconocido\((x, y)\) se encuentra ubicándolo en esta línea recta.

Variable
Independiente	Dependiente
\(x_{0}\)	\(y_{0}\)
\(x\)	\(y\)
\(x_{1}\)	\(y_{1}\)

Mesa\(\PageIndex{3}\)

Figura\(\PageIndex{7}\)

Así

\[\label{eq:125}\frac{y-y_{0}}{y_{1}-y_{0}}=\frac{x-x_{0}}{x_{1}-x_{0}} \]

de manera que, dado\(x\),

\[\label{eq:126}y=y_{0}+(x-x_{0})\frac{y_{1}-y_{0}}{x_{1}-x_{0}} \]

Interpolación Bilineal

La interpolación bilineal es una generalización bidimensional de la interpolación lineal. En la siguiente tabla\(f(\mathsf{D}) = f(x_{0}, y_{0}),\: f(\mathsf{A}) = f(x_{0}, y_{1}),\: f(\mathsf{F}) = f(x_{1}, y_{0})\),, y\(f(\mathsf{C}) = f(x_{1}, y_{1})\) se conocen y\(f(x, y)\) se encuentran. La técnica de interpolación bilineal se ilustra en la figura.

Variable
Independiente	Independiente	Dependiente
\(x_{0}\)	\(y_{0}\)	\(f_{0}\)
\(x\)	\(y\)	\(f\)
\(x_{1}\)	\(y_{1}\)	\(f_{1}\)

Mesa\(\PageIndex{4}\)

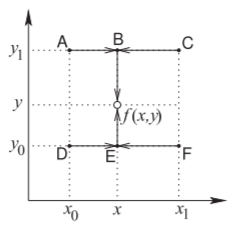
Figura\(\PageIndex{8}\)

Primero, encuentra el valor de la función en punto a\(\mathsf{B}\) partir de los valores en Punto\(\mathsf{A}\) y Punto\(\mathsf{C}\). Así, a partir de la ecuación\(\eqref{eq:126}\),

\[\label{eq:127}f(\mathsf{B})=f(x,y_{1})=f(\mathsf{A})+(x-x_{0})\frac{f(\mathsf{C})-f(\mathsf{A})}{x_{1}-x_{0}} \]

Del mismo modo

\[\label{eq:128}f(\mathsf{E})=f(x,y_{0})=f(\mathsf{D})+(x-x_{0})\frac{f(\mathsf{F})-f(\mathsf{D})}{x_{1}-x_{0}} \]

Interpolación lineal entre\(\mathsf{E}\) rendimientos de punto\(\mathsf{B}\) y punto

\[\label{eq:129}f(x,y)=f(\mathsf{E})+(y-y_{0})\frac{f(\mathsf{B})-f(\mathsf{E})}{y_{1}-y_{0}} \]

Combinando estos, la función obtenida de la interpolación bilineal es

\[\begin{align}f(x,y)&=\frac{f(x_{0},y_{0})}{(x_{1}-x_{0})(y_{1}-y_{0})}(x_{1}-x)(y_{1}-y)+\frac{f(x_{1},y_{0})}{(x_{1}-x_{0})(y_{1}-y_{0})}(x-x_{0})(y_{1}-y)\nonumber \\ \label{eq:130}&\quad +\frac{f(x_{0},y_{1})}{(x_{1}-x_{0})(y_{1}-y_{0})}(x_{1}-x)(y-y_{0})+\frac{f(x_{1},y_{1})}{(x_{1}-x_{0})(y_{1}-y_{0})}(x-x_{0})(y-y_{0})\end{align} \]

Al interpolar desde una tabla, elegir los puntos más cercanos al punto final producirá la mayor precisión.

1.A.13 Círculos en el Plano Complejo

Una situación común que ocurre cuando se trabaja con números complejos implica equiparar la magnitud de un número complejo siendo igual a un número real. Como se mostrará, esto define un círculo en el plano complejo. Considerar la relación

\[\label{eq:131}|S-c|=r \]

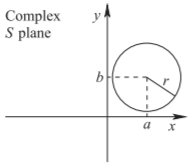
Figura\(\PageIndex{9}\): Un círculo en el\(S\) plano definido por la relación\(|S − c| = r\), dónde\(c = a + \jmath b\) y\(S = x +\jmath y\).

donde\(S = x +\jmath y\) y\(c = a +\jmath b\) son números complejos y\(r\) es un número real. Sustituyendo\(S\) y\(c\) en\(\eqref{eq:131}\) rendimientos de ecuaciones

\[\begin{align}\label{eq:132} |(x − a) +\jmath (y − b)| &= r \\ \label{eq:133}\text{that is,}\quad [(x − a) +\jmath (y − b)] [(x − a) − \jmath (y − b)] &= r^{2} \\ \label{eq:134} (x − a)^{2} + (y − b)^{2} &= r^{2}\end{align} \]

Lo anterior es una ecuación general para un círculo en el\(x-y\) plano con centro\((a, b)\) y radio\(r\) (ver Figura\(\PageIndex{9}\)).

1.A.14 Transformación bilineal

La transformación bilineal mapea un círculo en el plano complejo sobre otro círculo en el plano complejo [19]. La transformación bilineal de una variable compleja\(z\) es

\[\label{eq:135}w=\frac{Az+B}{Cz+1} \]

donde\(A,\: B\), y\(C\) son números reales. En el uso de RF y microondas,\(z\) y\(w\) podrían ser coeficientes de reflexión o impedancias. La reordenación de la ecuación\(\eqref{eq:133}\) da como resultado

\[\label{eq:136}w=\frac{A}{C}+\frac{B-\frac{A}{C}}{Cz+1} \]

que se puede reorganizar como

\[\label{eq:137}\frac{w-\frac{A}{C}}{B-\frac{A}{C}}=\frac{1}{Cz+1} \]

La complejidad de la derivación se reduce mediante la introducción de las variables intermedias\(W\) y\(Z\) se define como

\[\label{eq:138}W=\frac{w-\frac{A}{C}}{B-\frac{A}{C}} \]

y

\[\label{eq:139}Z=Cz+1 \]

y observando que, a partir de la ecuación\(\eqref{eq:137}\),

\[\label{eq:140}W=1/Z \]

Si, en Ecuación\(\eqref{eq:139}\), el locus de\(z\) describe un círculo, entonces el locus de también\(Z\) será un círculo ya que\(C\) es una constante. Si el centro del círculo en el\(Z\) espacio es\(C_{Z}\) y la distancia desde cualquier punto del círculo al centro es el radio\(R_{Z}\), entonces

\[\label{eq:141}|Z-C_{Z}|=R_{Z} \]

Considerando la ecuación\(\eqref{eq:139}\), entonces en el\(z\) espacio, el centro del círculo es

\[\label{eq:142}C_{z}=\frac{C_{Z}}{C}-\frac{1}{C} \]

y su radio es

\[\label{eq:143}R_{z}=R_{Z}/C \]

La eliminación de los signos de magnitud en la ecuación\(\eqref{eq:141}\) lleva a

\[\label{eq:144}(Z − C_{Z}) (Z − C_{Z})^{\ast} = (Z − C_{Z}) (Z^{\ast} − C^{\ast} Z) = R_{Z}^{2} \]

o

\[\label{eq:145}ZZ^{\ast} − C_{Z}Z^{\ast} − C_{Z}^{\ast}Z + (|CZ|^{2} − R_{Z}^{2})=0 \]

que es la ecuación general para un círculo en el plano complejo.

Ahora, el círculo en el\(Z\) avión estará relacionado con lo que sucede en el\(W\) avión. Sustituir la ecuación\(\eqref{eq:140}\) en la ecuación\(\eqref{eq:145}\) da como resultado

\[\label{eq:146}\frac{1}{WW^{\ast}}-C_{Z}\frac{1}{W^{\ast}}-C_{Z}^{\ast}\frac{1}{W} + (|CZ|^{2} − R_{Z}^{2})=0 \]

y reordenando,

\[\label{eq:147}WW^{\ast}-\frac{C_{Z}}{(|C_{Z}|^{2}-R_{Z}^{2})}W-\frac{C_{Z}^{\ast}}{(|C_{Z}|^{2}-R_{Z}^{2})}W^{\ast}+\frac{1}{(|C_{Z}|^{2}-R_{Z}^{2})}=0 \]

Esto está en la misma forma que Ecuación\(\eqref{eq:145}\), por lo que Ecuación\(\eqref{eq:147}\) describe un círculo en el\(W\) espacio con el centro

\[\label{eq:148}C_{W}=\frac{C_{Z}^{\ast}}{(|C_{Z}|^{2}-R_{Z}^{2})} \]

y radio

\[\label{eq:149}R_{W}=\left|\frac{R_{Z}}{|C_{Z}|^{2}-R_{Z}^{2}}\right| \]

Ahora el locus de también\(w\) será un círculo. A partir de la ecuación\(\eqref{eq:138}\),

\[\label{eq:150}w=W\left(B-\frac{A}{C}\right)+\frac{A}{C} \]

de manera que\(W\) se escala y se agrega una constante. El centro del círculo en el\(w\) espacio es

\[\label{eq:151}C_{w}=C_{W}\left(B-\frac{A}{C}\right)+\frac{A}{C}=\frac{C_{Z}^{\ast}(B-A/C)}{(|C_{Z}|^{2}-R_{Z}^{2})}+\frac{A}{C} \]

y el radio es

\[\label{eq:152}R_{w}=R_{W}\left|B-\frac{A}{C}\right|=\left|\frac{(B-A/C)}{|C_{Z}|^{2}-R_{Z}^{2}}\right| \]

Sustituyendo ecuaciones\(\eqref{eq:142}\) y\(\eqref{eq:143}\) en lo anterior relaciona los centros y radios en los\(z\) espacios\(w\) y:

\[\begin{align}\label{eq:153}C_{w}&=\frac{(CC_{z}+1)^{\ast}(B-A/C)}{(|CC_{z}+1|^{2}-|CR_{z}|^{2})}+\frac{A}{C} \\ \label{eq:154}R_{w}&=\left|\frac{(B-A/C)CR_{z}}{|CC_{z}+1|^{2}-|CR_{z}|^{2}}\right|=\left|\frac{(BC-A)R_{z}}{|CC_{z}+1|^{2}-|CR_{z}|^{2}}\right|\end{align} \]

Así, la transformada bilineal, Ecuación\(\eqref{eq:135}\), mapea todos los puntos de un círculo en el\(z\) plano a puntos en un círculo en el\(w\) plano.

1.A.15 Ecuaciones Cuadráticas y Cúbicas

Ecuación cuadrática

La forma general de la ecuación cuadrática en\(x\) es (\(a,\: b,\)y\(c\) puede ser compleja)

\[\label{eq:155}ax^{2}+bx+c=0 \]

donde\(a\neq 0\). Hay dos soluciones, llamadas raíces, dadas por la fórmula cuadrática, [20]

\[\label{eq:156}x=\frac{-b\pm\sqrt{b^{2}-4ac}}{2a} \]

e\(\pm\) indica dos posibles raíces,

\[\label{eq:157}x_{+}=\frac{-b+\sqrt{b^{2}-4ac}}{2a}\quad\text{and}\quad x_{-}=\frac{-b-\sqrt{b^{2}-4ac}}{2a} \]

Aunque\(a,\: b\), y\(c\) sean reales, las raíces pueden ser complejas y podrían ser degeneradas, es decir, las mismas. Los factores de la ecuación cuadrática provienen de las raíces, es decir,

\[\label{eq:158}ax^{2}+bx+c=a(x-x_{+})(x-x_{-}) \]

Ecuación cúbica

La forma general de la ecuación cúbica en\(x\) es (\(a,\: b,\: c\)y\(d\) puede ser compleja)

\[\label{eq:159}ax^{3}+bx^{2}+cx+d=0 \]

donde\(a\neq 0\). Hay tres soluciones, llamadas raíces, dadas por la fórmula cúbica, [20]

\[\label{eq:160}x_{k}=\frac{1}{3a}\left(b+u_{k}+\frac{\Delta_{0}}{u_{k}C}\right),\quad k\in\{1, 2, 3\} \]

donde las\(u_{k}\) s son las raíces cúbicas de uno:\(u_{1} = 1,\: u_{2} = \frac{1}{2}\left(-1+\jmath\sqrt{3}\right),\: u_{3} =\frac{1}{2}\left(−1 −\jmath\sqrt{3}\right),\) y

\[\label{eq:161}C=\left[\frac{1}{2}\left(\Delta_{1}+\sqrt{\Delta_{1}^{2}-4\Delta_{0}^{3}}\right)\right]^{1/3} \]

con\(\Delta_{0} = b^{2} − 3ac\) y\(\Delta_{1} = 2b^{3} − 9abc + 27a^{2}d\). En Ecuación se puede hacer\(\eqref{eq:161}\) cualquier elección de las raíces cuadradas o cúbicas ya que el efecto es simplemente intercambiar\(x_{1},\: x_{2}\) y\(x_{3}\). Tenga en cuenta que\(ax^{3} + bx^{2} + cx + d = (x − x_{1})(x − x_{2})(x − x_{3})\).

1.A.16 Método de Kron: Condensación de red

El método de Kron [21, 22, 23] también se llama condensación de red y se utiliza en el desarrollo de redes equivalentes más simples de grandes circuitos lineales con\(y\) parámetros algebraicos, es decir, para redes resistivas, o para circuitos lineales generales en análisis de dominio de frecuencia donde los\(y\) parámetros son números complejos. La condensación de red es un enfoque numérico particular para los circuitos. Es de uso en el modelado de orden reducido de circuitos lineales y en el diseño de filtros.

La formulación de admitancia nodal indefinida de una red con cuatro terminales externos (ver Figura\(\PageIndex{10}\)) es

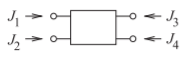
Figura\(\PageIndex{10}\): Una red de cuatro terminales.

\[\label{eq:162}\left[\begin{array}{ccccc}{y_{11}}&{y_{12}}&{\cdots}&{y_{1,k}}&{y_{1,k+1}}\\{y_{21}}&{y_{22}}&{\cdots}&{y_{2,k}}&{y_{2,k+1}}\\{\vdots}&{\vdots}&{\ddots}&{\vdots}&{\vdots}\\{y_{k1}}&{y_{k2}}&{\cdots}&{y_{k,k}}&{y_{k,k+1}}\\{y_{k+1,1}}&{y_{k+1,2}}&{\cdots}&{y_{k+1,k}}&{y_{k+1,k+1}}\end{array}\right]\left[\begin{array}{c}{v_{1}}\\{v_{2}}\\{v_{3}}\\{v_{4}}\\{v_{5}}\\{\vdots}\\{v_{k}}\\{v_{k+1}}\end{array}\right]=\left[\begin{array}{c}{J_{1}}\\{J_{2}}\\{J_{3}}\\{J_{4}}\\{0}\\{\vdots}\\{0}\\{0}\end{array}\right] \]

ya que no hay fuentes de corriente externas en los terminales internos\(5,\: 6,\:\cdots\: , k+1\). Dado que\((k+1)\) la fuente de corriente es cero, la\((k + 1)\) fila y la columna de\(\mathbf{Y}\) pueden eliminarse, rindiendo

\[\label{eq:163}\left[\begin{array}{cccc}{y_{11}'}&{y_{12}'}&{\cdots}&{y_{1,k}'}\\{y_{21}'}&{y_{22}'}&{\cdots}&{y_{2,k}'}\\{\vdots}&{\vdots}&{\ddots}&{\vdots}\\{y_{k1}'}&{y_{k2}'}&{\cdots}&{y_{k,k}'}\end{array}\right]\left[\begin{array}{c}{v_{1}'}\\{v_{2}'}\\{v_{3}'}\\{v_{4}'}\\{v_{5}'}\\{\vdots}\\{v_{k}'}\end{array}\right]=\left[\begin{array}{c}{J_{1}}\\{J_{2}}\\{J_{3}}\\{J_{4}}\\{0}\\{\vdots}\\{0}\end{array}\right] \]

donde

\[\label{eq:164}y_{ij}'=y_{ij}-y_{k+1, j}\frac{y_{i,k+1}}{y_{k+1,k+1}}\quad\text{and}\quad v_{i}'=v_{i}-v_{k+1} \]

No es motivo de preocupación que se hayan alterado los voltajes de los terminales, ya que a todos se les ha agregado la misma cantidad. Esto tiene el mismo efecto que elegir otro terminal de referencia. El terminal de referencia es arbitrario hasta que se conecta al circuito completo. El proceso puede continuar hasta que las ecuaciones de red se reduzcan a la de un elemento de cuatro terminales, es decir

\[\label{eq:165}\left[\begin{array}{cccc}{y_{11}''}&{y_{12}''}&{y_{13}''}&{y_{14}''}\\{y_{21}''}&{y_{22}''}&{y_{23}''}&{y_{24}''}\\{y_{31}''}&{y_{32}''}&{y_{33}''}&{y_{34}''}\\{y_{41}''}&{y_{42}''}&{y_{43}''}&{y_{44}''}\end{array}\right]\left[\begin{array}{c}{v_{1}''}\\{v_{2}''}\\{v_{3}''}\\{v_{4}''}\end{array}\right]=\left[\begin{array}{c}{J_{1}}\\{J_{2}}\\{J_{3}}\\{J_{4}}\end{array}\right] \]

La matriz\(y\) -parámetro en Ecuación\(\eqref{eq:165}\) es la del elemento de cuatro terminales que se muestra en la Figura\(\PageIndex{10}\).

Notas al pie

[1] La ingeniería eléctrica externa\(\imath\) (\(i\)sin el punto) se utiliza para\(\sqrt{−1}\), pero esta se reemplaza por\(\jmath\) (\(j\)sin el punto) en ingeniería eléctrica para evitar confusiones con el uso de\(i\) para corriente.