2.1: Introducción

Una línea de transmisión almacena energía eléctrica y magnética, y para una señal alterna en una posición en la línea, la energía se convierte de una forma a otra a medida que avanza el tiempo. Como tal línea tiene una forma de circuito que combina inductores,\(L\) s (para la energía magnética), condensadores,\(C\) s (para la energía eléctrica) y resistencias,\(R\) s (pérdidas de modelado), cuyos valores dependen de la geometría de la línea y las propiedades del material.

Las líneas de transmisión consideradas en este capítulo están restringidas a solo dos conductores paralelos, como se muestra en la Figura\(\PageIndex{1}\), siendo la distancia entre los dos hilos (es decir, en la dirección transversal) sustancialmente menor que las longitudes de onda de las señales en la línea. La interpretación física correcta es que los conductores de una línea de transmisión confinan y guían un campo EM. El campo EM contiene la energía de la señal y no la corriente en la línea.

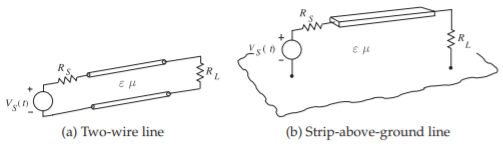
Figura\(\PageIndex{1}\): Líneas de transmisión de dos conductores.

Sin embargo, con dimensiones transversales eléctricamente pequeñas, una línea de dos conductores puede analizarse satisfactoriamente sobre la base de tensiones y corrientes.

La comprensión más temprana de la transmisión de la señal condujo a la telegrafía a distancias. El paso teórico crítico que permitió la transmisión a distancias más que cortas fue el desarrollo de una comprensión de la transmisión de señales en líneas mediante análisis fasor [1]. Este análisis de dominio de frecuencia sigue siendo la mejor manera de entender las líneas de transmisión. Esta teoría de líneas de transmisión con desarrollos modernos se presenta en la Sección 2.2 y fórmulas y conceptos útiles desarrollados en la Sección 2.3 para líneas de transmisión sin pérdidas. La sección 2.4 presenta varias configuraciones de líneas sin pérdidas que son particularmente útiles en el diseño de circuitos de microondas y utilizadas en muchos lugares de esta serie de libros. La Sección 2.5 repite el análisis de líneas sin pérdida pero ahora para líneas con pérdida. Reflexiones y transmisión de potencia en múltiples interfaces interactuantes se considera en la Sección 2.6. Importantes modelos de red para líneas de transmisión se desarrollan en la Sección 2.7. La última sección, Sección 2.8, presenta fórmulas de resumen para muchas líneas de transmisión de dos conductores.

2.1.1 Cuándo debe considerarse una línea de transmisión

El determinante clave de si una línea de transmisión puede considerarse como una conexión invisible entre dos puntos es si la señal en cualquier lugar a lo largo de la interconexión tiene el mismo valor en un instante particular. Si el valor de la señal (digamos, voltaje) varía a lo largo de la línea (en un instante), entonces puede ser necesario considerar los efectos de la línea de transmisión. Un criterio típico utilizado es que si la longitud de la interconexión es menor que la\(1/20\) th de la longitud de onda del componente de frecuencia más alta de una señal, entonces los efectos de la línea de transmisión pueden ignorarse de manera segura y el circuito se puede modelar como un solo\(RLC\) circuito [2]. El umbral real utilizado—\(\lambda/20,\: \lambda/10\), o\(\lambda/5\) —se basa en la experiencia y la aplicación particular. Por ejemplo, una interconexión que lleva una señal digital que se registra en\(4\text{ GHz}\) tiene una componente de frecuencia apreciable en\(20\text{ GHz}\). Entonces la interconexión alcanza el\(\lambda/10\) umbral cuando es\(4.5\text{ mm}\) larga. Por lo tanto, toma un tiempo finito para que la variación de una tensión en un extremo de la interconexión impacte en la tensión en el otro extremo. El límite último está determinado por la velocidad de la luz\(c\), pero ésta se ve reducida por la permitividad relativa y permeabilidad del material en el que existen los campos. La permitividad y permeabilidad relativas describen el efecto del exceso de almacenamiento de energía potencial en el material, por encima del vacío, de manera análoga a almacenar energía mecánica en un resorte.

2.1.2 Movimiento de una señal en una línea de transmisión

Una línea coaxial (Figura\(\PageIndex{2}\) (a)) es la línea de transmisión por excelencia ya que es una de las pocas estructuras de líneas de transmisión que se pueden describir exactamente desde los primeros principios cuando no hay pérdida. Esto se debe a que la sección transversal de una línea coaxial coincide con el sistema de coordenadas cilíndricas, un sistema de coordenadas ortogonales con condiciones de contorno que se pueden expresar en términos de una sola coordenada (el radio). Se sabe cómo resolver las ecuaciones de Maxwell, que son solo ecuaciones diferenciales, en un sistema de coordenadas ortogonales. Esto se hace para una línea coaxial en la Sección 2.9.

Cuando se aplica un pulso de voltaje positivo al conductor central del

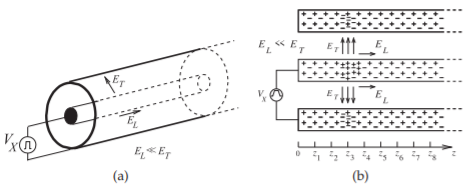
Figura\(\PageIndex{2}\): Una línea de transmisión coaxial: (a) vista tridimensional; (b) la línea con fuente de voltaje pulsado que muestra los campos eléctricos en un instante en el tiempo a medida que un pulso de voltaje viaja por la línea. \(E_{L} ≪ E_{T}\).

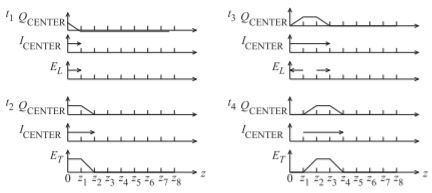
Figura\(\PageIndex{3}\): Campos, corrientes y cargas en la línea de transmisión coaxial de la Figura\(\PageIndex{2}\) a veces\(t_{4} > t_{3} > t_{2} > t_{1}\). \(Q_{\text{CENTER}}\)es el cargo neto gratuito en el conductor central. \(I_{\text{CENTER}}\)es la corriente en el conductor central.

línea coaxial, como se muestra en la Figura\(\PageIndex{2}\) (a), resulta un campo eléctrico que se dirige desde el conductor central al conductor externo. Haciendo referencia a la Figura\(\PageIndex{2}\) (b), se denota el componente del campo que se dirige a lo largo de la trayectoria más corta desde el conductor central hasta el conductor externo\(E_{T}\), y el subíndice\(T\) denota la componente transversal del campo con el plano transversal siendo perpendicular al dirección de propagación a lo largo de la línea. La figura\(\PageIndex{2}\) (b) muestra los campos en la estructura después de que el pulso haya comenzado a moverse a lo largo de la línea. Esto se muestra en otra vista de la Figura\(\PageIndex{3}\) en cuatro momentos diferentes. El voltaje transversal,\(V_{T}\), viene dado por\(E_{T}\) integrado a lo largo de una trayectoria entre los conductores interno y externo:\(V_{T} ≈ E_{T}(a − b)\). Esta es una buena medida, siempre que las dimensiones transversales sean pequeñas en comparación con una longitud de onda (de lo contrario la integral es entonces dependiente de la trayectoria). El pulso de voltaje que excita la línea tiene una forma trapezoidal y la Figura\(\PageIndex{3}\) muestra la carga\(Q_{\text{CENTER}}\),, y la corriente\(I_{\text{CENTER}}\),, en el conductor central y el campo transversal,\(E_{T}\). El voltaje entre el conductor interno y externo tiene la misma forma que\(E_{T}\). Como indican las ecuaciones de Maxwell, un cambio en el tiempo del campo eléctrico da como resultado un cambio espacial en el campo magnético y, por lo tanto, en la corriente. Como resultado hay una variación de la corriente en el tiempo y esto da como resultado un cambio espacial del campo eléctrico. La búsqueda de una variación de tiempo a una variación espacial y luego de regreso a una variación de tiempo hace que el pulso se mueva hacia abajo en la línea.

El pulso se mueve hacia abajo por la línea a la velocidad del grupo, que para una línea coaxial sin pérdidas es la misma que la velocidad de fase,\(v_{p}\). \(^{1}\)Esto está determinado por las propiedades físicas de la región entre los conductores. La permitividad,\(\varepsilon\), describe el almacenamiento de energía asociado al campo eléctrico\(E\),, y el almacenamiento de energía asociado al campo magnético,\(H\), se describe por la permeabilidad,\(\mu\). (Ambos\(\varepsilon\) y\(\mu\) son propiedades del medio, el material). Se ha determinado que\(^{2}\)

\[\label{eq:1}v_{p}=1/\sqrt{\mu\varepsilon} \]

En vacío\(\varepsilon =\varepsilon_{0}\), la permitividad del espacio libre y\(\mu =\mu_{0}\) la permeabilidad del espacio libre. Estas son constantes físicas y tienen los valores

\[\begin{array}{ll}{\text{Permittivity of free space:}}&{\varepsilon_{0}=8.854\times 10^{-12}\text{ F/m}}\\{\text{Permeability of free space:}}&{\mu_{0}=4\pi\times 10^{-7}\text{ H/m}}\end{array}\nonumber \]

Una conclusión aquí es que la energía EM se puede almacenar en el espacio libre, es decir, en un vacío. En espacio libre\(v_{p} = c = 1/\sqrt{\mu_{0}\varepsilon_{0}} = 3\times 10^{8}\text{ m/s}\). Las longitudes de onda del espacio libre\(\lambda_{0} = c/f\), a varias frecuencias\(f\), son

\(f\)	\(100\text{ MHz}\)	\(1\text{ GHz}\)	\(10\text{ GHz}\)
\(\lambda_{0}\)	\(3\text{ m}\)	\(30\text{ cm}\)	\(3.0\text{ cm}\)

Mesa\(\PageIndex{1}\)

Comúnmente\(\lambda_{0}\) se usa para indicar la longitud de onda en el espacio libre y\(\lambda_{g}\), la longitud de onda guía, se usa para denotar la longitud de onda en una línea de transmisión. Es conveniente utilizar la permitividad relativa (o el término menos utilizado constante dieléctrica)\(\varepsilon_{r}\), definida como

\[\label{eq:2}\varepsilon_{r}=\varepsilon/\varepsilon_{0} \]

De manera similar, la permeabilidad relativa es

\[\label{eq:3}\mu_{r}=\mu/\mu_{0} \]

y la mayoría de los materiales tienen\(\mu_{r} = 1\). La permitividad, permeabilidad y conductividad de los materiales utilizados en los circuitos de RF y microondas se dan en el Apéndice 2.A.

Ejemplo\(\PageIndex{1}\): Transmission Line Wavelength

Una longitud de línea coaxial se llena con un dieléctrico que tiene una permitividad relativa de\(20\) y está diseñado para ser\(1/4\) longitud de onda larga a una frecuencia,\(f\), de\(1.850\text{ GHz}\).

1. ¿Cuál es la longitud de onda del espacio libre?
2. ¿Cuál es la longitud de onda de la señal en la línea coaxial llena de dieléctrico?
3. ¿Cuánto dura la línea?

Solución

1. \(\lambda_{0} = c/f = 3\times 10^{8}/1.85\times 10^{9} = 0.162\text{ m} = 16.2\text{ cm}\).
2. Tenga en cuenta que para una línea llena de dieléctrico con\(\mu_{r} = 1,\:\lambda = v_{p}/f = c/(\sqrt{\varepsilon_{r}}f) = \lambda_{0}/\sqrt{\varepsilon_{r}}\), entonces\(\lambda =\lambda_{0}/\sqrt{\varepsilon_{r}} = 16.2\text{ cm}/ \sqrt{20} = 3.62\text{ cm}\).
3. \(\lambda_{g}/4=3.62\text{ cm}/4=9.05\text{ mm}\).

Notas al pie

[1] La velocidad de fase es la velocidad aparente de un punto de fase constante en una onda sinusoidal y es casi independiente de la frecuencia para una línea coaxial de baja pérdida de pequeñas dimensiones transversales (menores que\(\lambda/10\)).

[2] Esto se deriva de las ecuaciones de Maxwell y describe la situación en la que los campos tienen una estructura muy simple, en general donde los campos se dirigen únicamente en el plano transversal.