4.4: Multimodo en líneas de transmisión

El multimodo es un fenómeno que afecta la integridad de una señal a medida que viaja en una línea de transmisión. Para las líneas de transmisión, el multimodo ocurre cuando hay dos o más configuraciones de campo EM que pueden soportar una onda de propagación. Diferentes configuraciones de campo viajan a diferentes velocidades de manera que la información que viaja en dos o modos modos se combinaría de manera incoherente y, si la energía en los modos es comparable, será imposible discernir la información pretendida que se está enviando. Es fundamental que las dimensiones de las estructuras de líneas de transmisión se diseñen para evitar el multimodo. El modo más común en una línea de transmisión es cuando no hay variación, o la mínima posible, de los campos en la dirección transversal (perpendicular a la dirección de propagación).

Las estructuras de transmisión de interés aquí son aquellas que tienen conductores que establecen condiciones de límite para guiar una ola a lo largo de un camino previsto. Para estas líneas, el modo de orden más bajo con variaciones mínimas de campo transversal se denomina modo TEM. Los modos de orden superior ocurren cuando los campos pueden variar. A partir de aquí la discusión invoca necesariamente la teoría EM. Si necesita hacer esto, consulte la Sección 1.5, donde se revisa la teoría EM específicamente con respecto al multimodo. Uno de los conceptos importantes es que las paredes eléctricas y magnéticas imponen condiciones límite en los campos. Las paredes eléctricas son conductores, mientras que una pared magnética se forma aproximadamente en la interfaz de dos regiones que tienen diferente permitividad.

Es propiedad de los campos EM que las variaciones espaciales de los campos no pueden ocurrir con demasiada rapidez. Esto viene directamente de las ecuaciones de Maxwell que relacionan la derivada espacial (la derivada con respecto a la distancia) del campo eléctrico con la derivada temporal del campo magnético. Lo mismo ocurre con la variación espacial del campo magnético y la variación temporal del campo eléctrico. La rapidez con que un campo varía con el tiempo depende de la frecuencia. La rapidez con que un campo EM cambia espacialmente, su rizo, depende de la longitud de onda relativa a la geometría y de las condiciones de contorno. Sin paredes eléctricas y magnéticas que establezcan condiciones de límite, como en el espacio libre, se requiere una longitud de onda completa para obtener la variación de orden más bajo de los campos. Con paredes eléctricas o magnéticas donde los campos pueden terminar, una distancia menor es suficiente. Entre dos paredes eléctricas se requiere media longitud de onda de distancia. Lo mismo ocurre con las paredes magnéticas. Con una pared eléctrica y una pared magnética, una separación de cuarto de longitud de onda de las paredes soportará un modo de orden superior. A

	Campo E	Campo H
Pared eléctrica	Normal	Paralelo
Pared magnética	Paralelo	Normal

Tabla\(\PageIndex{1}\): Propiedades de los campos EM en paredes eléctricas y magnéticas.

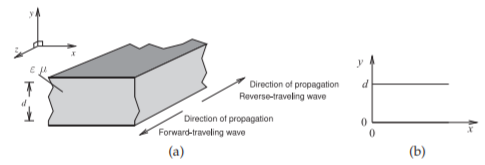
Figura\(\PageIndex{1}\): Guía de ondas de placa paralela: (a) vista tridimensional; y (b) vista transversal (transversal).

regla general para evitar el multimodo es que las geometrías transversales críticas deben mantenerse por debajo de una fracción de una longitud de onda (digamos,\(<\lambda/2\) o\(<\lambda/4\)).

Ya se ha descrito un tipo de multimodo. En el capítulo anterior se vio que las señales en una línea de transmisión regular tienen dos soluciones simples que se interpretan como los modos de desplazamiento hacia adelante y hacia atrás. Cada modo es una posible solución de las ecuaciones diferenciales que describen las señales. Estos no son los modos a los que se hace referencia con el término multimodal. Las condiciones límite en la dirección longitudinal son establecidas por las impedancias de fuente y carga, por lo que la variación puede ser cualquier fracción de una longitud de onda. Esta sección se refiere a otras soluciones a las ecuaciones que describen los campos en una estructura de línea de transmisión. En general, las otras soluciones surgen cuando las dimensiones transversales, como la distancia entre los dos conductores de una línea de transmisión de dos conductores, permiten una variación de los campos.

Las condiciones límite establecidas en las paredes eléctricas y magnéticas se derivaron en la Sección 1.8 y se resumen en la Tabla\(\PageIndex{1}\). Las estructuras de circuitos como líneas de transmisión, espesores de sustrato y geometrías relacionadas casi siempre se eligen para que solo sea posible una solución de las ecuaciones de Maxwell. En particular, si las dimensiones transversales de una línea de transmisión son mucho menores que una longitud de onda, entonces será imposible que los campos se acurruquen sobre sí mismos y así tal vez solo haya una o, en algunos casos, ninguna solución a las ecuaciones de Maxwell.