2.2: Redes individuales y doblemente terminadas

Los filtros son generalmente redes de dos puertos y proporcionan la máxima transferencia de potencia desde una fuente a una carga en un rango de frecuencia especificado mientras rechazan la transmisión de señales a otras frecuencias. Dos posibles redes de filtro se muestran en la Figura\(\PageIndex{1}\). La red en la Figura\(\PageIndex{1}\) (a) se conoce como una red doblemente terminada, ya que ambos puertos están terminados resistivamente.

Figura\(\PageIndex{1}\): Redes terminadas.

La red en la Figura\(\PageIndex{1}\) (b) se llama una red terminada de manera individual, ya que solo un puerto termina en una resistencia. La red doblemente terminada está mucho más cerca del tipo de red requerida en RF donde las cargas y las impedancias de origen son finitas. Una red de terminación individual es aplicable en algunas aplicaciones de circuitos integrados de RF donde está involucrada muy poca potencia de RF y, a menudo, cuando se usa retroalimentación. En tales casos, la salida de un amplificador RFIC puede aproximarse a una fuente de voltaje ideal ya que la impedancia de la fuente equivalente Thevenin puede ser insignificante. La mayor parte de la síntesis de redes de filtro terminadas por separado utiliza un procedimiento análogo al que se presenta aquí para filtros doblemente terminados.

2.2.1 Redes de doble terminación

El procedimiento de síntesis de filtros establecido para redes de filtros doblemente terminadas se enfoca en realizar el coeficiente de reflexión de entrada. Para un filtro sin pérdidas el cuadrado de la magnitud del coeficiente de reflexión es uno menos el cuadrado de la pérdida de inserción y este es el origen de este método que se llama el método de pérdida de inserción.

El coeficiente de reflexión de entrada de la red doblemente terminada en la Figura\(\PageIndex{1}\) (a) es

\[\label{eq:1}\Gamma_{1}(s)=\frac{Z_{\text{in, 1}}(s)-R_{S}}{Z_{\text{in, 1}}(s)+R_{S}} \]

donde la impedancia de referencia es la resistencia de la fuente, RS, y s es la variable Laplace. En la banda de paso de un filtro el coeficiente de reflexión es aproximadamente cero.

Hay varios otros parámetros utilizados en el diseño de filtros y estos se introducirán ahora. La relación de potencia del transductor (TPR) se define como

\[\begin{align}\text{TPR}&=\frac{\text{Maximum power available from the source}}{\text{Power absorbed by the load}}\nonumber \\ \label{eq:2}&=\frac{\frac{1}{2}(V_{g}(s)/2)^{2}/R_{S}}{\frac{1}{2}V_{2}^{2}(s)/R_{L}}=\left|\frac{1}{2}\sqrt{\frac{R_{L}}{R_{S}}}\frac{V_{g}(s)}{V_{2}(s)}\right|^{2}\end{align} \]

El coeficiente de transmisión,\(T(s)\), de la red es

\[\label{eq:3}T(s)=\frac{1}{\sqrt{\text{TPR}(s)}}=2\sqrt{\frac{R_{S}}{R_{L}}}\frac{V_{2}(s)}{V_{g}(s)} \]

SI el filtro no tiene pérdidas, la pérdida de inserción (IL) (o función del transductor) es

\[\label{eq:4}\text{IL}(s)=\text{TPR}(s)=[1/T(s)]^{2} \]

El siguiente paso en el desarrollo del procedimiento de síntesis de filtros es la introducción de la función característica, definida como la relación de los coeficientes de reflexión y transmisión:

\[\label{eq:5}K(s)=\frac{\Gamma_{1}(s)}{T(s)}=\frac{N(s)}{D(s)} \]

donde\(N\) está la función numeradora y\(D\) es la función denominador. Idealmente la red de filtros es sin pérdidas y así, desde el principio de conservación de energía, la suma de las magnitudes cuadradas de los coeficientes de transmisión y reflexión debe ser unidad:

\[\label{eq:6}|T(s)|^{2}+|\Gamma_{1}(s)|^{2}=1 \]

Es decir,

\[\label{eq:7}|T(s)|^{2}=1-|\Gamma_{1}(s)|^{2} \]

Dividir ambos lados de la ecuación\(\eqref{eq:7}\) por\(|T(s)|^{2}\) resultados en

\[\label{eq:8}1=\frac{1}{|T(s)|^{2}}-\frac{|\Gamma_{1}(s)|^{2}}{|T(s)|^{2}} \]

o

\[\label{eq:9}1=|\text{IL}(s)|-|K(s)|^{2} \]

La reordenación de la ecuación\(\eqref{eq:9}\) conduce a

\[\label{eq:10}|\text{IL}(s)|=1+|K(s)|^{2} \]

y así

\[\label{eq:11}|T(s)|^{2}=\frac{1}{1+|K(s)|^{2}} \]

y

\[\label{eq:12}|\Gamma_{1}(s)|^{2}=\frac{|K(s)|^{2}}{1+|K(s)|^{2}} \]

En lo anterior se ve que tanto los coeficientes de reflexión como los de transmisión son funciones de la función característica de la red de dos puertos. Se ha alcanzado un hito. En un filtro RF, la pérdida de inserción dependiente de la frecuencia o el coeficiente de transmisión es de mayor importancia, ya que estos están directamente relacionados con el flujo de potencia. \(\eqref{eq:11}\)La ecuación muestra que esto puede expresarse en términos de otra función,, que\(K(s)\), a partir de la ecuación\(\eqref{eq:5}\), se puede expresar como la relación de\(N(s)\) y\(D(s)\). Para circuitos de elementos grumados,\(N(s)\) y\(D(s)\) son polinomios.

2.2.2 Respuesta del filtro de paso bajo

Como ejemplo de la relación de las diversas respuestas de filtro, considere las respuestas de filtro de paso bajo sin pérdidas que se muestran en la Figura\(\PageIndex{1}\). Este filtro tiene una respuesta de paso bajo con una frecuencia de esquina expresada en radianes como\(\omega_{c} = 1\text{ rad/s}\). Idealmente\(T(s)\) para\(s\leq\jmath\) (nota\(s =\jmath\omega\)) sería uno, y para\(s>\jmath\),\(T(s)\) sería cero. No es posible realizar tal respuesta ideal, y la respuesta que se muestra en la Figura\(\PageIndex{2}\) (a) es típica de lo que se puede lograr. El coeficiente de reflexión se muestra en la Figura\(\PageIndex{2}\) (b), con la función característica\(K(s)\) mostrada en la Figura\(\PageIndex{2}\) (c). Si\(|K(s)|^{2}\) se expresa como la relación de dos polinomios (es decir, as\(N(s)/D(s)\)), entonces se puede ver a partir de la Figura\(\PageIndex{2}\) (e y f) que los ceros del coeficiente de reflexión\(|\Gamma_{1}(s)|^{2}\),, son también los ceros de\(N(s)\). Además, se observa que los ceros del coeficiente de transmisión también son los ceros de\(D(s)\), como se muestra en la Figura\(\PageIndex{2}\) (a y c).

El primer objetivo en el diseño de filtros de elementos agrupados es el desarrollo de la función de transferencia de la red en el dominio de frecuencia o, de manera equivalente, el\(s\) dominio. \(^{1}\)La función de transferencia de entrada-salida del filtro genérico en la Figura\(\PageIndex{3}\) es

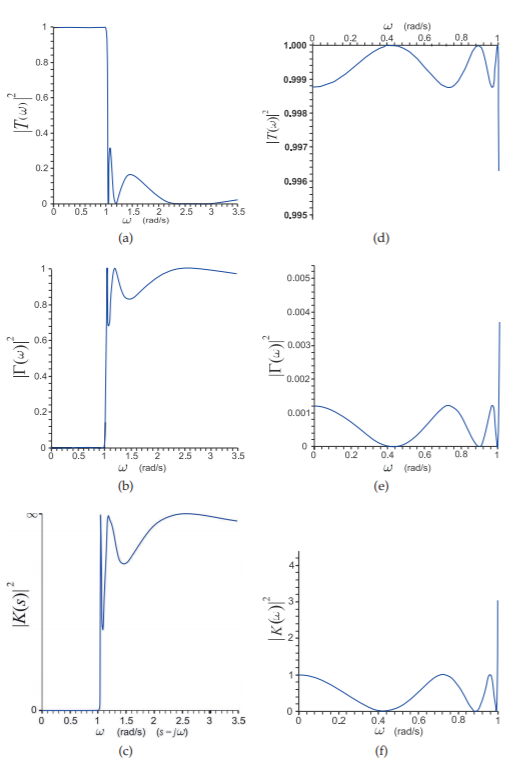
Figura\(\PageIndex{2}\): Un ejemplo de un filtro de paso bajo en términos de diversas respuestas: (a) coeficiente de transmisión; (b) respuesta de coeficiente de reflexión; y (c) respuesta de función característica. Las respuestas detalladas se muestran en (d), (e) y (f), respectivamente.

Figura\(\PageIndex{3}\): Filtro genérico.

\[\label{eq:13}T(s)=Y(s)/X(s) \]

y el procedimiento de diseño es hacer coincidir esta respuesta con una respuesta definida por la relación de dos polinomios:

\[\label{eq:14}T(s)=\frac{N(s)}{D(s)}=\frac{a_{m}s^{m}+a_{m-1}s^{m-1}+\cdots +a_{1}s+a_{0}}{s^{n}+b_{n-1}s^{n-1}+\cdots +b_{1}s+b_{0}} \]

Aquí\(N\) significa numerador y\(D\) denominador, y estos no son los mismos que los de Ecuación\(\eqref{eq:5}\) (donde solo eran etiquetas para numerador y denominador). La respuesta del filtro usando una descripción polo-cero se puede sintetizar para que el proceso de diseño comience reescribiendo la ecuación\(\eqref{eq:14}\) explícitamente en términos de ceros,\(z_{m}\), y polos,\(p_{n}\):

\[\label{eq:15}T(s)=\frac{N(s)}{D(s)}=\frac{a_{m}(s+z_{1})(s+z_{2})\cdots (s+z_{m-1})(s+z_{m})}{(s+p_{1})(s+p_{2})\cdots (s+p_{n-1})(s+p_{n})} \]

Ya que sólo la respuesta de frecuencia es de interés\(s =\jmath\omega\), simplificando así el análisis para señales sinusoidales.

Los polos y ceros pueden ser números complejos y se pueden trazar en el\(s\) plano complejo. Las condiciones impuestas por los circuitos realizables requieren que\(D(s)\) sea un polinomio de Hurwitz,\(^{2}\) lo que asegura que sus polos estén ubicados en el plano de la mitad izquierda. \(N(s)\)determina la ubicación de los ceros de transmisión del filtro, y el orden de\(N(s)\) no puede ser mayor que el orden de\(D(s)\). Es decir,\(n\geq m\) para que el filtro tenga respuesta finita o cero a frecuencia infinita

Se pueden emplear dos estrategias para derivar la respuesta del filtro. El primero es derivar los polinomios\(N(s)\) y\(D(s)\) en Ecuación\(\eqref{eq:14}\). Esto parece un problema abierto, pero se descubrió en las décadas de 1950 y 1960 que en situaciones normales solo hay algunos tipos de respuestas útiles que son descritas por algunos polinomios, incluidos Butterworth, Bessel, Chebyshev y Cauer.

Notas al pie

[1] Se está teniendo cuidado en el uso de la terminología ya que\(s\) puede ser compleja con algunos tipos de filtros, pero estos filtros se realizan mediante procesamiento digital de señales.

[2] Un polinomio de Hurwitz es un polinomio cuyos coeficientes son números reales positivos y cuyos ceros se encuentran en la mitad izquierda del\(s\) plano complejo.