2.4: La aproximación de paso bajo máximamente plana (Butterworth)

Los filtros Butterworth tienen una respuesta máxima plana (Figura\(\PageIndex{1}\)) que en el dominio del tiempo corresponde a un sistema amortiguado críticamente.

2.4.1 Diseño de filtro Butterworth

Los filtros Butterworth tienen la función de transferencia

\[\label{eq:1}T(s)=\frac{N(s)}{D(s)}=\frac{k}{s^{n}+b_{n-1}s^{n-1}+\cdots +b_{1}s+b_{0}} \]

Esta es una respuesta de todos los polos. El polinomio característico del filtro Butterworth es

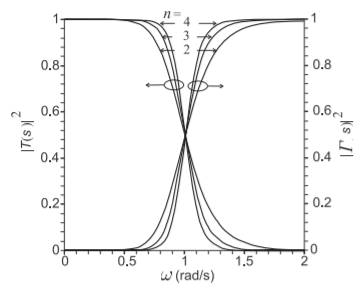
Figura\(\PageIndex{1}\): Aproximación de filtro de paso bajo máximamente plano, o Butterworth, para varios órdenes\(n\),, del filtro.

\(n\)	Factores de\(B_{n}(s)\)
\ (n\) ">\(1\)	\ (B_ {n} (s)\)” class="lt-eng-46098">\((s + 1)\)
\ (n\) ">\(2\)	\ (B_ {n} (s)\)” class="lt-eng-46098">\((s^{2} + 1.4142s + 1)\)
\ (n\) ">\(3\)	\ (B_ {n} (s)\)” class="lt-eng-46098">\((s + 1)(s^{2} + s + 1)\)
\ (n\) ">\(4\)	\ (B_ {n} (s)\)” class="lt-eng-46098">\((s^{2} + 0.7654s + 1)(s^{2} + 1.8478s + 1)\)
\ (n\) ">\(5\)	\ (B_ {n} (s)\)” class="lt-eng-46098">\((s + 1)(s^{2} + 0.6180s + 1)(s^{2} + 1.6180s + 1)\)
\ (n\) ">\(6\)	\ (B_ {n} (s)\)” class="lt-eng-46098">\((s^{2} + 0.5176s + 1)(s^{2} + 1.4142s + 1)(s^{2} + 1.9319s + 1)\)
\ (n\) ">\(7\)	\ (B_ {n} (s)\)” class="lt-eng-46098">\((s + 1)(s^{2} + 0.4450s + 1)(s^{2} + 1.2470s + 1)(s^{2} + 1.8019s + 1)\)
\ (n\) ">\(8\)	\ (B_ {n} (s)\)” class="lt-eng-46098">\((s^{2} + 0.3902 + 1)(s^{2} + 1.1111s + 1)(s^{2} + 1.6629s + 1)(s^{2} + 1.9616s + 1)\)

Cuadro\(\PageIndex{1}\): Factores del\(B_{n}(s)\) polinomio.

\[\label{eq:2}|K(s)|^{2}=|s^{2n}|=\omega^{2n} \]

desde\(s =\jmath\omega\) y dónde\(n\) está el orden de la función. Así, el coeficiente de transmisión es

\[\label{eq:3}|T(s)|^{2}=\frac{1}{1+|K(s)|^{2}}=\frac{1}{1+|s^{2n}|}=\frac{1}{1+\omega^{2n}} \]

que a menudo se escribe como

\[\label{eq:4}|T(s)|^{2}=\frac{1}{1+|K(s)|^{2}}=\frac{1}{B_{n}(s)B_{n}(-s)} \]

En la comunidad filtrante,\(B_{n}(s)\) se llama el polinomio Butterworth y tiene la forma general

\[\label{eq:5}B_{n}(s)=\left\{\begin{array}{ll}{\prod_{k=1}^{n/2}\left[s^{2}-2s\cos\left(\frac{2k+n-1}{2n}\pi\right)+1\right]}&{\text{for }n\text{ even}}\\{(s+1)\prod_{k=1}^{(n-1)/2}\left[s^{2}-2s\cos\left(\frac{2k+n-1}{2n}\pi\right)+1\right]}&{\text{for }n\text{ odd}}\end{array}\right. \]

\(B_{n}(s)\)se da en forma factorizada en la Tabla\(\PageIndex{1}\). Una mayor factorización de los factores de segundo orden da como resultado raíces conjugadas complejas, por lo que generalmente se dejan en la forma mostrada.

La percepción se obtiene examinando el polinomio característico para una frecuencia real de radián,\(\omega\) (donde\(s =\jmath\omega\)), en los siguientes puntos de frecuencia:

\[\begin{align}\label{eq:6}\text{at }\omega &=0\quad \to\quad |T(0)|^{2}=\frac{1}{1+0}=1 \\ \label{eq:7}\text{at }\omega&=1\quad\to\quad |T(1)|^{2}=\frac{1}{1+1}=\frac{1}{2}\end{align} \]

Por lo tanto, la respuesta de transmisión del filtro está a la mitad de la potencia en la frecuencia de esquina\(\omega = 1\). Otra observación es que los coeficientes de transmisión en\(\omega = 0\) y\(\omega = 1\) son independientes del grado del polinomio característico. Esto se muestra en la Figura\(\PageIndex{1}\), donde se trazan las respuestas de los filtros Butterworth para tres órdenes diferentes.

2.4.2 Construcción de la Función de Transferencia

A menudo la función característica\(K\),, se especifica en términos de la variable\(\omega\), y para fines de síntesis la respuesta debe transformarse de nuevo al\(s\) dominio. Como ejemplo, considere la función máximamente plana de tercer orden con un polinomio característico igual a\(\omega^{3}\) (de la ecuación\(\eqref{eq:3}\)):

\[\label{eq:8}K(\omega)=\omega^{3}\quad\text{and}\quad |T(\omega)|^{2}=\frac{1}{1+\omega^{6}} \]

(Obsérvese que aquí las seis primeras derivadas de\(|K(s)|^{2}\) con respecto a\(s\) son cero at\(s = 0\).) Entonces, a partir de la Ecuación (2.2.7),

\[\label{eq:9}|\Gamma_{1}(\omega)|^{2}=1-\frac{1}{1+\omega^{6}}=\frac{\omega^{6}}{1+\omega^{6}} \]

A frecuencias reales (es decir, frecuencias que se encuentran en el eje imaginario en el\(s\) plano)

\[\label{eq:10}s=\jmath\omega,\quad\text{so}\quad\omega=s/\jmath=-\jmath s \]

Así, en el\(s\) dominio, el coeficiente de reflexión se convierte

\[\label{eq:11}|\Gamma_{1}(\jmath\omega)|^{2}=|\Gamma_{1}(\jmath(-\jmath s))|^{2}=|\Gamma_{1}(s)|^{2}=\frac{(-\jmath s)^{6}}{1+(-\jmath s)^{6}} \]

Es decir,

\[\label{eq:12}|\Gamma_{1}(s)|^{2}=\frac{-s^{6}}{1-s^{6}}=\Gamma_{1}(s)\Gamma_{1}(-s) \]

Factorizar los rendimientos polinómicos del denominador

\[\label{eq:13}1-s^{6}=(1-s)(1+s)(s^{2}+s+1)(s^{2}-s+1) \]

Al elegir aquellos factores con raíces sólo en el plano de la mitad izquierda (requeridos para una red realizable), se obtienen los ceros del denominador. Ahora el numerador de\(|\Gamma_{1}(s)|^{2}\) se factoriza fácilmente, y como este es de tercer orden, solo tiene tres ceros de reflexión en DC. La función resultante es

\[\label{eq:14}\Gamma_{1}(s)=\frac{s^{3}}{(s+1)(s^{2}+s+1)} \]

y así

\[\label{eq:15}T(s)=\frac{1}{(s+1)(s^{2}+s+1)} \]

Este ejemplo ilustra cómo\(\Gamma_{1}(s)\) y se\(T(s)\) puede obtener de\(K(s)\). Este procedimiento se generaliza en la siguiente sección.

2.4.3 Aproximación\(n\) de Reflexión de Orden Th

Siguiendo el procedimiento esbozado en la sección anterior, la generalización conduce a la respuesta de Butterworth de\(n\) orden th:

\[\begin{align}|\Gamma_{1}(s)|^{2}&=\Gamma_{1}(s)\cdot\Gamma_{1}(-s)\nonumber \\ \label{eq:16}&=\frac{(-s^{2})^{n}}{1+(-s^{2})^{n}}=\frac{(-s^{2})^{n}}{\prod_{i=1}^{n}(s-s_{i})\cdot\prod_{j=n+1}^{2n}(s-s_{j})}\end{align} \]

Así\(|\Gamma_{1}(s)|^{2}\) tiene\(n\) las raíces (estas son las\(s_{i}\) s) que se encuentran en el\(s\) plano de la mitad izquierda, y\(n\) las raíces (las\(s_{j}\) s) que se encuentran en el\(s\) plano de la mitad derecha. Tenga en cuenta que\(j\) se utiliza como índice y\(\jmath\) (\(\jmath\), sin el punto) representa\(\sqrt{-1}\). Es razonable agrupar todas las raíces planas de la mitad izquierda juntas (no se podría sintetizar un circuito si hubiera una raíz de plano de la mitad derecha) para que

\[\label{eq:17}\Gamma_{1}(s)=\frac{(-s)^{n}}{\prod_{i=1}^{n}(s-s_{i})} \]

Resolver las raíces del denominador de la ecuación\(\eqref{eq:16}\) (es decir, encontrar las raíces de\(1 +(-s^{2})^{n} = 0\)) produce las siguientes raíces en el\(s\) plano de la mitad izquierda:

\[\label{eq:18}s_{i}=\exp\left\{\jmath (2i-1+n)\frac{\pi}{2n}\right\}\quad i=1,2,\ldots ,n \]

donde\(\exp (\jmath\theta) = \cos (\theta) + \jmath\sin (\theta)\).

Ejemplo\(\PageIndex{1}\): Reflection Coefficient Derivation for Butterworth Filter

Desarrollar el coeficiente de reflexión a partir de las raíces del prototipo de filtro de paso bajo\((n = 3)\) Butterworth de tercer orden.

Solución

De la ecuación\(\eqref{eq:18}\) las tres raíces son

\[\begin{align}\label{eq:19}s_{1}&=\exp\left\{\jmath(2\times 1-1+3)\frac{\pi}{2\times 3}\right\}=\exp\left\{\jmath\frac{2}{3}\pi\right\} \\ \label{eq:20}s_{2}&=\exp\left\{\jmath(2\times 2-1+3)\frac{\pi}{2\times 3}\right\}=\exp\left\{\jmath\:\pi\right\} \\ \label{eq:21}s_{3}&=\exp\left\{\jmath(2\times 3-1+3)\frac{\pi}{2\times 3}\right\}=\exp\left\{\jmath\frac{4}{3}\pi\right\}\end{align} \]

y el coeficiente de reflexión de entrada del filtro normalizado a\(1\:\Omega\) es

\[\label{eq:22}\Gamma_{1}(s)=\frac{s^{3}}{\left(s+\frac{1}{2}-\jmath\frac{\sqrt{3}}{2}\right)(s+1)\left(s+\frac{1}{2}+\jmath\frac{\sqrt{3}}{2}\right)}=\frac{s^{3}}{(s+1)(s^{2}+s+1)} \]

Esto es lo mismo que Ecuación\(\eqref{eq:14}\).

2.4.4 Consideración del Ancho de

En la frecuencia de esquina de la respuesta de Butterworth, es decir, en\(1\text{ rad/s}\), la respuesta de transmisión está\(3\text{ dB}\) por debajo de su respuesta de transferencia máxima.

Orden,\(n\)
\ (n\) ">\(n=3\)	\(4\)	\(5\)	\(6\)	\(7\)	\(8\)	\(9\)	\(10\)
\ (n\) ">\(0.798\text{ rad/s}\)	\(0.844\)	\(0.873\)	\(0.901\)	\(0.908\)	\(0.919\)	\(0.928\)	\(0.935\)

Cuadro\(\PageIndex{2}\): Frecuencias radianas en las que la respuesta de un filtro Butterworth es\(1\text{ dB}\) descendente para una frecuencia de esquina\(f_{0} = 0.1592\text{ Hz}\) (\(\omega_{0} = 1\text{ rad/s}\)). En\(f_{0}\) la transmisión la respuesta está abajo\(3\text{ dB}\).

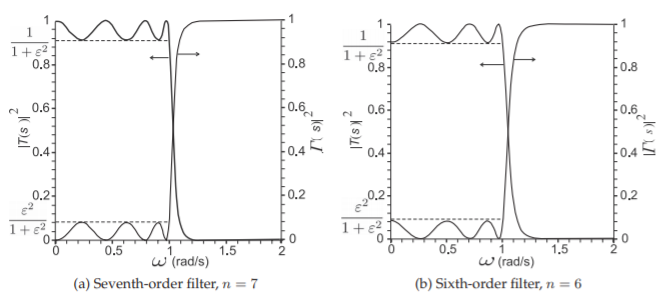
Figura\(\PageIndex{2}\): Respuestas del filtro paso bajo de Chebyshev. En decibelios, la ondulación es\(R_{\text{dB}} = −10 \log[1/(1 + \varepsilon^{2})] = 10 \log(1 + \varepsilon^{2})\),\(\varepsilon\) se llama el factor de ondulación.

En ocasiones, los filtros de microondas están diseñados para tener\(1\text{ dB}\) anchos de banda. Las frecuencias radianas a las que las respuestas de diversos órdenes de filtros Butterworth están\(1\text{ dB}\) abajo se dan en la Tabla\(\PageIndex{2}\). Al escalar la frecuencia de la respuesta de Butterworth, el filtro se puede diseñar para un\(1\text{ dB}\) ancho de banda específico.