2.7: Filtros Butterworth y Chebyshev
- Page ID
- 85191
Los filtros de paso bajo de\(n\) orden th construidos a partir de los polinomios Butterworth y Chebyshev tienen las formas de circuito de escalera de la Figura\(\PageIndex{1}\) (a o b). La figura\(\PageIndex{1}\) utiliza varias anotaciones taquivadas comúnmente utilizadas con filtros. Primero, tenga en cuenta que existen dos formas prototipo designadas Tipo\(1\) y Tipo\(2\), y estas son referidas como duales entre sí. Las dos formas prototipo tienen respuestas idénticas con los mismos valores numéricos de elementos\(g_{1},\ldots , g_{n}\). Considere el\(1\) prototipo Tipo de la Figura\(\PageIndex{1}\) (a). El elemento más a la derecha es la carga resistiva, que también se conoce como el elemento\((n + 1)\) th. El siguiente elemento a la izquierda de esto es un condensador de derivación (de valor\(g_{n}\)) si\(n\) es par, o un inductor en serie (de valor\(g_{n}\)) si\(n\) es impar. Entonces, para el\(1\) prototipo Type, el condensador de derivación al lado de la carga no existe si\(n\) es impar. La misma interpretación se aplica al circuito de la Figura\(\PageIndex{1}\) (b).
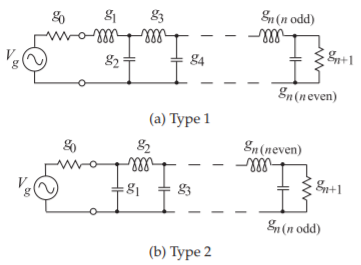
Figura\(\PageIndex{1}\): Prototipos de filtro en la topología de Cauer. Aquí\(n\) está el orden del filtro.
| Orden,\(n\) | \(2\) | \(3\) | \(4\) | \(5\) | \(6\) | \(7\) | \(8\) | \(9\) |
|---|---|---|---|---|---|---|---|---|
| \ (n\) ">\(g_{1}\) | \ (2\) ">\(1.4142\) | \ (3\) ">\(1\) | \ (4\) ">\(0.7654\) | \ (5\) ">\(0.6180\) | \ (6\) ">\(0.5176\) | \ (7\) ">\(0.4450\) | \ (8\) ">\(0.3902\) | \ (9\) ">\(0.3473\) |
| \ (n\) ">\(g_{2}\) | \ (2\) ">\(1.4142\) | \ (3\) ">\(2\) | \ (4\) ">\(1.8478\) | \ (5\) ">\(1.6180\) | \ (6\) ">\(1.4142\) | \ (7\) ">\(1.2470\) | \ (8\) ">\(1.1111\) | \ (9\) ">\(1\) |
| \ (n\) ">\(g_{3}\) | \ (2\) ">\(1\) | \ (3\) ">\(1\) | \ (4\) ">\(1.8478\) | \ (5\) ">\(2\) | \ (6\) ">\(1.9318\) | \ (7\) ">\(1.8019\) | \ (8\) ">\(1.6629\) | \ (9\) ">\(1.5321\) |
| \ (n\) ">\(g_{4}\) | \ (2\) "> | \ (3\) ">\(1\) | \ (4\) ">\(0.7654\) | \ (5\) ">\(1.6180\) | \ (6\) ">\(1.9318\) | \ (7\) ">\(2\) | \ (8\) ">\(1.9615\) | \ (9\) ">\(1.8794\) |
| \ (n\) ">\(g_{5}\) | \ (2\) "> | \ (3\) "> | \ (4\) ">\(1\) | \ (5\) ">\(0.6180\) | \ (6\) ">\(1.4142\) | \ (7\) ">\(1.8019\) | \ (8\) ">\(1.9615\) | \ (9\) ">\(2\) |
| \ (n\) ">\(g_{6}\) | \ (2\) "> | \ (3\) "> | \ (4\) "> | \ (5\) ">\(1\) | \ (6\) ">\(0.5176\) | \ (7\) ">\(1.2470\) | \ (8\) ">\(1.6629\) | \ (9\) ">\(1.8794\) |
| \ (n\) ">\(g_{7}\) | \ (2\) "> | \ (3\) "> | \ (4\) "> | \ (5\) "> | \ (6\) ">\(1\) | \ (7\) ">\(0.4450\) | \ (8\) ">\(1.1111\) | \ (9\) ">\(1.5321\) |
| \ (n\) ">\(g_{8}\) | \ (2\) "> | \ (3\) "> | \ (4\) "> | \ (5\) "> | \ (6\) "> | \ (7\) ">\(1\) | \ (8\) ">\(0.3902\) | \ (9\) ">\(1\) |
| \ (n\) ">\(g_{9}\) | \ (2\) "> | \ (3\) "> | \ (4\) "> | \ (5\) "> | \ (6\) "> | \ (7\) "> | \ (8\) ">\(1\) | \ (9\) ">\(0.3473\) |
| \ (n\) ">\(g_{10}\) | \ (2\) "> | \ (3\) "> | \ (4\) "> | \ (5\) "> | \ (6\) "> | \ (7\) "> | \ (8\) "> | \ (9\) ">\(1\) |
Cuadro\(\PageIndex{1}\): Coeficientes del filtro prototipo de paso bajo Butterworth normalizados a una frecuencia de esquina de radianes\(1\text{ rad/s}\) y una impedancia\(1\:\Omega\) del sistema (i.e.,\(g_{0} =1= g_{n+1}\)).
2.7.1 Filtro Butterworth
Una generalización del ejemplo de la sección anterior conduce a una fórmula para los valores de elementos de un circuito de escalera que implementa un filtro de paso bajo Butterworth. Para una respuesta máxima plana o Butterworth, los valores de los elementos del circuito en la Figura\(\PageIndex{1}\) (a y b) son
\[\label{eq:1}g_{r}=2\sin\left\{ (2r-1)\frac{\pi}{2n}\right\}\quad r=1,2,3,\ldots ,n \]
y\(g_{0} =1= g_{n+1}\). En la tabla se\(\PageIndex{1}\) enumeran los coeficientes de los filtros prototipo de paso bajo Butterworth hasta el noveno orden.
Ejemplo\(\PageIndex{1}\): Fourth-Order Butterworth Lowpass Filter
Derivar el prototipo de paso bajo Butterworth de cuarto orden de Type\(1\).
Solución
De la ecuación\(\eqref{eq:1}\),
\[\begin{align}\label{eq:2} g_{1}&=2\sin [\pi /(2\cdot 4)]=0.765369\text{ H} \\ \label{eq:3} g_{2}&=2\sin [3\pi /(2\cdot 4)]=1.847759\text{ F} \\ \label{eq:4} g_{3}&=2\sin [5\pi /(2\cdot 4)]=1.847759\text{ H} \\ \label{eq:5} g_{4}&=2\sin [7\pi /(2\cdot 4)]= 0.765369\text{ F}\end{align} \]
Así, el circuito prototipo de paso bajo Butterworth de cuarto orden con una frecuencia de esquina\(1\text{ rad/s}\) es como se muestra en la Figura\(\PageIndex{2}\).
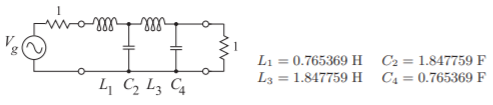
Figura\(\PageIndex{2}\): Prototipo de filtro de paso bajo Butterworth de cuarto orden.
2.7.2 Filtro Chebyshev
Para una respuesta de Chebyshev, los valores de elemento del prototipo de paso bajo mostrado en la Figura\(\PageIndex{1}\) se encuentran a partir de la fórmula recursiva [1, 6, 7]:
\[\begin{align}\label{eq:6} g_{0}&=1\quad g_{1}=\frac{2a_{1}}{\gamma} \\ \label{eq:7} g_{n+1}&=\left\{\begin{array}{ll}{1}&{n\text{ odd}} \\ {\tanh^{2}(\beta /4)}&{n\text{ even}}\end{array}\right\} \\ \label{eq:8}g_{k}&=\frac{4a_{k-1}a_{k}}{b_{k-1}g_{k-1}},\quad k=1,2,\ldots ,n \\ \label{eq:9}a_{k}&=\sin\left[\frac{(2k-1)\pi}{2n}\right]\quad k=1,2,\ldots ,n\end{align} \]
donde
\[\begin{align}\label{eq:10}\gamma&=\sinh\left(\frac{\beta}{2n}\right) \\ \label{eq:11} b_{k}&=\gamma^{2}+\sin^{2}\left(\frac{k\pi}{n}\right)\quad k=1,2,\ldots ,n \\ \label{eq:12}\beta &=\ln\left[\coth\left(\frac{R_{\text{dB}}}{2\cdot 20\log(2)}\right)\right] = \ln\left[\coth\left(\frac{R_{\text{dB}}}{17.3717793}\right)\right] \\ \label{eq:13}R_{\text{dB}}&=10\log(1+\varepsilon^{2})\end{align} \]
\(n\)es el orden del filtro, y\(\varepsilon\) es el factor de ondulación y define el nivel de la ondulación en términos absolutos. \(R_{\text{dB}}\)es la ondulación expresada en decibelios (la ondulación se especifica generalmente en decibelios).
Un punto interesante a tener en cuenta aquí es que la resistencia de origen, cuyo valor viene dado por\(g_{0}\), y la resistencia de terminación, cuyo valor viene dado por\(g_{n+1}\), son solo iguales para filtros de orden impar. Para un filtro Chebyshev de orden par la resistencia de terminación,\(g_{n+1}\), será diferente y una función de la ondulación del filtro. Debido a que generalmente es deseable tener impedancias idénticas de fuente y carga, los filtros Chebyshev casi siempre están restringidos a un orden impar. Así, los prototipos de Chebyshev de orden impar son como se muestra en la Figura\(\PageIndex{3}\).
Además, para una función de grado impar (\(n\)es impar) hay una coincidencia perfecta en DC,
\[\label{eq:14}|T(0)|^{2}=1 \]
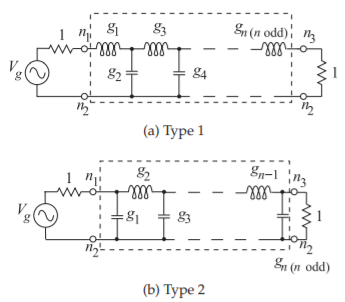
Figura\(\PageIndex{3}\): Prototipos de filtro paso bajo Chebyshev de orden impar en la topología de Cauer. Aquí\(n\) está el orden del filtro.
| Orden Ondulación | \(n=3\) | |||||
|---|---|---|---|---|---|---|
| \(0.01\text{ dB}\) | \(0.1\text{ dB}\) | \(0.2\text{ dB}\) | \(1.0\text{ dB}\) | \(3.0\text{ dB}\) | \(\varepsilon =0.1\) | |
| \(g_{1}\) | \ (n=3\)\(0.01\text{ dB}\)\(n=5\)\(0.01\text{ dB}\)\(n=7\)\(0.01\text{ dB}\)\(n=9\)\(0.01\text{ dB}\) “>\(0.62918\) | \ (n=3\)\(0.1\text{ dB}\)\(n=5\)\(0.1\text{ dB}\)\(n=7\)\(0.1\text{ dB}\)\(n=9\)\(0.1\text{ dB}\) “>\(1.03156\) | \ (n=3\)\(0.2\text{ dB}\)\(n=5\)\(0.2\text{ dB}\)\(n=7\)\(0.2\text{ dB}\)\(n=9\)\(0.2\text{ dB}\) “>\(1.22754\) | \ (n=3\)\(1.0\text{ dB}\)\(n=5\)\(1.0\text{ dB}\)\(n=7\)\(1.0\text{ dB}\)\(n=9\)\(1.0\text{ dB}\) “>\(2.02359\) | \ (n=3\)\(3.0\text{ dB}\)\(n=5\)\(3.0\text{ dB}\)\(n=7\)\(3.0\text{ dB}\)\(n=9\)\(3.0\text{ dB}\) “>\(3.34874\) | \ (n=3\)\(\varepsilon =0.1\)\(n=5\)\(\varepsilon =0.1\)\(n=7\)\(\varepsilon =0.1\)\(n=9\)\(\varepsilon =0.1\) “>\(0.85158\) |
| \(g_{2}\) | \ (n=3\)\(0.01\text{ dB}\)\(n=5\)\(0.01\text{ dB}\)\(n=7\)\(0.01\text{ dB}\)\(n=9\)\(0.01\text{ dB}\) “>\(0.97028\) | \ (n=3\)\(0.1\text{ dB}\)\(n=5\)\(0.1\text{ dB}\)\(n=7\)\(0.1\text{ dB}\)\(n=9\)\(0.1\text{ dB}\) “>\(1.14740\) | \ (n=3\)\(0.2\text{ dB}\)\(n=5\)\(0.2\text{ dB}\)\(n=7\)\(0.2\text{ dB}\)\(n=9\)\(0.2\text{ dB}\) “>\(1.15254\) | \ (n=3\)\(1.0\text{ dB}\)\(n=5\)\(1.0\text{ dB}\)\(n=7\)\(1.0\text{ dB}\)\(n=9\)\(1.0\text{ dB}\) “>\(0.99410\) | \ (n=3\)\(3.0\text{ dB}\)\(n=5\)\(3.0\text{ dB}\)\(n=7\)\(3.0\text{ dB}\)\(n=9\)\(3.0\text{ dB}\) “>\(0.71170\) | \ (n=3\)\(\varepsilon =0.1\)\(n=5\)\(\varepsilon =0.1\)\(n=7\)\(\varepsilon =0.1\)\(n=9\)\(\varepsilon =0.1\) “>\(1.10316\) |
| \(g_{3}\) | \ (n=3\)\(0.01\text{ dB}\)\(n=5\)\(0.01\text{ dB}\)\(n=7\)\(0.01\text{ dB}\)\(n=9\)\(0.01\text{ dB}\) “>\(0.62918\) | \ (n=3\)\(0.1\text{ dB}\)\(n=5\)\(0.1\text{ dB}\)\(n=7\)\(0.1\text{ dB}\)\(n=9\)\(0.1\text{ dB}\) “>\(1.03156\) | \ (n=3\)\(0.2\text{ dB}\)\(n=5\)\(0.2\text{ dB}\)\(n=7\)\(0.2\text{ dB}\)\(n=9\)\(0.2\text{ dB}\) “>\(1.22754\) | \ (n=3\)\(1.0\text{ dB}\)\(n=5\)\(1.0\text{ dB}\)\(n=7\)\(1.0\text{ dB}\)\(n=9\)\(1.0\text{ dB}\) “>\(2.02359\) | \ (n=3\)\(3.0\text{ dB}\)\(n=5\)\(3.0\text{ dB}\)\(n=7\)\(3.0\text{ dB}\)\(n=9\)\(3.0\text{ dB}\) “>\(3.34874\) | \ (n=3\)\(\varepsilon =0.1\)\(n=5\)\(\varepsilon =0.1\)\(n=7\)\(\varepsilon =0.1\)\(n=9\)\(\varepsilon =0.1\) “>\(0.85158\) |
| Orden Ondulación | \(n=5\) | |||||
| \(0.01\text{ dB}\) | \(0.1\text{ dB}\) | \(0.2\text{ dB}\) | \(1.0\text{ dB}\) | \(3.0\text{ dB}\) | \(\varepsilon =0.1\) | |
| \(g_{1}\) | \ (n=3\)\(0.01\text{ dB}\)\(n=5\)\(0.01\text{ dB}\)\(n=7\)\(0.01\text{ dB}\)\(n=9\)\(0.01\text{ dB}\) “>\(0.75633\) | \ (n=3\)\(0.1\text{ dB}\)\(n=5\)\(0.1\text{ dB}\)\(n=7\)\(0.1\text{ dB}\)\(n=9\)\(0.1\text{ dB}\) “>\(1.14681\) | \ (n=3\)\(0.2\text{ dB}\)\(n=5\)\(0.2\text{ dB}\)\(n=7\)\(0.2\text{ dB}\)\(n=9\)\(0.2\text{ dB}\) “>\(1.33944\) | \ (n=3\)\(1.0\text{ dB}\)\(n=5\)\(1.0\text{ dB}\)\(n=7\)\(1.0\text{ dB}\)\(n=9\)\(1.0\text{ dB}\) “>\(2.13488\) | \ (n=3\)\(3.0\text{ dB}\)\(n=5\)\(3.0\text{ dB}\)\(n=7\)\(3.0\text{ dB}\)\(n=9\)\(3.0\text{ dB}\) “>\(3.48129\) | \ (n=3\)\(\varepsilon =0.1\)\(n=5\)\(\varepsilon =0.1\)\(n=7\)\(\varepsilon =0.1\)\(n=9\)\(\varepsilon =0.1\) “>\(0.97140\) |
| \(g_{2}\) | \ (n=3\)\(0.01\text{ dB}\)\(n=5\)\(0.01\text{ dB}\)\(n=7\)\(0.01\text{ dB}\)\(n=9\)\(0.01\text{ dB}\) “>\(1.30492\) | \ (n=3\)\(0.1\text{ dB}\)\(n=5\)\(0.1\text{ dB}\)\(n=7\)\(0.1\text{ dB}\)\(n=9\)\(0.1\text{ dB}\) “>\(1.37121\) | \ (n=3\)\(0.2\text{ dB}\)\(n=5\)\(0.2\text{ dB}\)\(n=7\)\(0.2\text{ dB}\)\(n=9\)\(0.2\text{ dB}\) “>\(1.33702\) | \ (n=3\)\(1.0\text{ dB}\)\(n=5\)\(1.0\text{ dB}\)\(n=7\)\(1.0\text{ dB}\)\(n=9\)\(1.0\text{ dB}\) “>\(1.09111\) | \ (n=3\)\(3.0\text{ dB}\)\(n=5\)\(3.0\text{ dB}\)\(n=7\)\(3.0\text{ dB}\)\(n=9\)\(3.0\text{ dB}\) “>\(0.76192\) | \ (n=3\)\(\varepsilon =0.1\)\(n=5\)\(\varepsilon =0.1\)\(n=7\)\(\varepsilon =0.1\)\(n=9\)\(\varepsilon =0.1\) “>\(1.37208\) |
| \(g_{3}\) | \ (n=3\)\(0.01\text{ dB}\)\(n=5\)\(0.01\text{ dB}\)\(n=7\)\(0.01\text{ dB}\)\(n=9\)\(0.01\text{ dB}\) “>\(1.57731\) | \ (n=3\)\(0.1\text{ dB}\)\(n=5\)\(0.1\text{ dB}\)\(n=7\)\(0.1\text{ dB}\)\(n=9\)\(0.1\text{ dB}\) “>\(1.97500\) | \ (n=3\)\(0.2\text{ dB}\)\(n=5\)\(0.2\text{ dB}\)\(n=7\)\(0.2\text{ dB}\)\(n=9\)\(0.2\text{ dB}\) “>\(2.16605\) | \ (n=3\)\(1.0\text{ dB}\)\(n=5\)\(1.0\text{ dB}\)\(n=7\)\(1.0\text{ dB}\)\(n=9\)\(1.0\text{ dB}\) “>\(3.00092\) | \ (n=3\)\(3.0\text{ dB}\)\(n=5\)\(3.0\text{ dB}\)\(n=7\)\(3.0\text{ dB}\)\(n=9\)\(3.0\text{ dB}\) “>\(4.53755\) | \ (n=3\)\(\varepsilon =0.1\)\(n=5\)\(\varepsilon =0.1\)\(n=7\)\(\varepsilon =0.1\)\(n=9\)\(\varepsilon =0.1\) “>\(1.80136\) |
| \(g_{4}\) | \ (n=3\)\(0.01\text{ dB}\)\(n=5\)\(0.01\text{ dB}\)\(n=7\)\(0.01\text{ dB}\)\(n=9\)\(0.01\text{ dB}\) “>\(1.30492\) | \ (n=3\)\(0.1\text{ dB}\)\(n=5\)\(0.1\text{ dB}\)\(n=7\)\(0.1\text{ dB}\)\(n=9\)\(0.1\text{ dB}\) “>\(1.37121\) | \ (n=3\)\(0.2\text{ dB}\)\(n=5\)\(0.2\text{ dB}\)\(n=7\)\(0.2\text{ dB}\)\(n=9\)\(0.2\text{ dB}\) “>\(1.33702\) | \ (n=3\)\(1.0\text{ dB}\)\(n=5\)\(1.0\text{ dB}\)\(n=7\)\(1.0\text{ dB}\)\(n=9\)\(1.0\text{ dB}\) “>\(1.09111\) | \ (n=3\)\(3.0\text{ dB}\)\(n=5\)\(3.0\text{ dB}\)\(n=7\)\(3.0\text{ dB}\)\(n=9\)\(3.0\text{ dB}\) “>\(0.76192\) | \ (n=3\)\(\varepsilon =0.1\)\(n=5\)\(\varepsilon =0.1\)\(n=7\)\(\varepsilon =0.1\)\(n=9\)\(\varepsilon =0.1\) “>\(1.37208\) |
| \(g_{5}\) | \ (n=3\)\(0.01\text{ dB}\)\(n=5\)\(0.01\text{ dB}\)\(n=7\)\(0.01\text{ dB}\)\(n=9\)\(0.01\text{ dB}\) “>\(0.75633\) | \ (n=3\)\(0.1\text{ dB}\)\(n=5\)\(0.1\text{ dB}\)\(n=7\)\(0.1\text{ dB}\)\(n=9\)\(0.1\text{ dB}\) “>\(1.14681\) | \ (n=3\)\(0.2\text{ dB}\)\(n=5\)\(0.2\text{ dB}\)\(n=7\)\(0.2\text{ dB}\)\(n=9\)\(0.2\text{ dB}\) “>\(1.33944\) | \ (n=3\)\(1.0\text{ dB}\)\(n=5\)\(1.0\text{ dB}\)\(n=7\)\(1.0\text{ dB}\)\(n=9\)\(1.0\text{ dB}\) “>\(2.13488\) | \ (n=3\)\(3.0\text{ dB}\)\(n=5\)\(3.0\text{ dB}\)\(n=7\)\(3.0\text{ dB}\)\(n=9\)\(3.0\text{ dB}\) “>\(3.48129\) | \ (n=3\)\(\varepsilon =0.1\)\(n=5\)\(\varepsilon =0.1\)\(n=7\)\(\varepsilon =0.1\)\(n=9\)\(\varepsilon =0.1\) “>\(0.97140\) |
| Orden Ondulación | \(n=7\) | |||||
| \(0.01\text{ dB}\) | \(0.1\text{ dB}\) | \(0.2\text{ dB}\) | \(1.0\text{ dB}\) | \(3.0\text{ dB}\) | \(\varepsilon =0.1\) | |
| \(g_{1}\) | \ (n=3\)\(0.01\text{ dB}\)\(n=5\)\(0.01\text{ dB}\)\(n=7\)\(0.01\text{ dB}\)\(n=9\)\(0.01\text{ dB}\) “>\(0.79694\) | \ (n=3\)\(0.1\text{ dB}\)\(n=5\)\(0.1\text{ dB}\)\(n=7\)\(0.1\text{ dB}\)\(n=9\)\(0.1\text{ dB}\) “>\(1.18118\) | \ (n=3\)\(0.2\text{ dB}\)\(n=5\)\(0.2\text{ dB}\)\(n=7\)\(0.2\text{ dB}\)\(n=9\)\(0.2\text{ dB}\) “>\(1.37226\) | \ (n=3\)\(1.0\text{ dB}\)\(n=5\)\(1.0\text{ dB}\)\(n=7\)\(1.0\text{ dB}\)\(n=9\)\(1.0\text{ dB}\) “>\(2.16656\) | \ (n=3\)\(3.0\text{ dB}\)\(n=5\)\(3.0\text{ dB}\)\(n=7\)\(3.0\text{ dB}\)\(n=9\)\(3.0\text{ dB}\) “>\(3.51852\) | \ (n=3\)\(\varepsilon =0.1\)\(n=5\)\(\varepsilon =0.1\)\(n=7\)\(\varepsilon =0.1\)\(n=9\)\(\varepsilon =0.1\) “>\(1.00794\) |
| \(g_{2}\) | \ (n=3\)\(0.01\text{ dB}\)\(n=5\)\(0.01\text{ dB}\)\(n=7\)\(0.01\text{ dB}\)\(n=9\)\(0.01\text{ dB}\) “>\(1.39242\) | \ (n=3\)\(0.1\text{ dB}\)\(n=5\)\(0.1\text{ dB}\)\(n=7\)\(0.1\text{ dB}\)\(n=9\)\(0.1\text{ dB}\) “>\(1.42281\) | \ (n=3\)\(0.2\text{ dB}\)\(n=5\)\(0.2\text{ dB}\)\(n=7\)\(0.2\text{ dB}\)\(n=9\)\(0.2\text{ dB}\) “>\(1.37820\) | \ (n=3\)\(1.0\text{ dB}\)\(n=5\)\(1.0\text{ dB}\)\(n=7\)\(1.0\text{ dB}\)\(n=9\)\(1.0\text{ dB}\) “>\(1.11151\) | \ (n=3\)\(3.0\text{ dB}\)\(n=5\)\(3.0\text{ dB}\)\(n=7\)\(3.0\text{ dB}\)\(n=9\)\(3.0\text{ dB}\) “>\(0.77220\) | \ (n=3\)\(\varepsilon =0.1\)\(n=5\)\(\varepsilon =0.1\)\(n=7\)\(\varepsilon =0.1\)\(n=9\)\(\varepsilon =0.1\) “>\(1.43678\) |
| \(g_{3}\) | \ (n=3\)\(0.01\text{ dB}\)\(n=5\)\(0.01\text{ dB}\)\(n=7\)\(0.01\text{ dB}\)\(n=9\)\(0.01\text{ dB}\) “>\(1.74813\) | \ (n=3\)\(0.1\text{ dB}\)\(n=5\)\(0.1\text{ dB}\)\(n=7\)\(0.1\text{ dB}\)\(n=9\)\(0.1\text{ dB}\) “>\(2.09667\) | \ (n=3\)\(0.2\text{ dB}\)\(n=5\)\(0.2\text{ dB}\)\(n=7\)\(0.2\text{ dB}\)\(n=9\)\(0.2\text{ dB}\) “>\(2.27566\) | \ (n=3\)\(1.0\text{ dB}\)\(n=5\)\(1.0\text{ dB}\)\(n=7\)\(1.0\text{ dB}\)\(n=9\)\(1.0\text{ dB}\) “>\(3.09364\) | \ (n=3\)\(3.0\text{ dB}\)\(n=5\)\(3.0\text{ dB}\)\(n=7\)\(3.0\text{ dB}\)\(n=9\)\(3.0\text{ dB}\) “>\(4.63898\) | \ (n=3\)\(\varepsilon =0.1\)\(n=5\)\(\varepsilon =0.1\)\(n=7\)\(\varepsilon =0.1\)\(n=9\)\(\varepsilon =0.1\) “>\(1.93981\) |
| \(g_{4}\) | \ (n=3\)\(0.01\text{ dB}\)\(n=5\)\(0.01\text{ dB}\)\(n=7\)\(0.01\text{ dB}\)\(n=9\)\(0.01\text{ dB}\) “>\(1.63313\) | \ (n=3\)\(0.1\text{ dB}\)\(n=5\)\(0.1\text{ dB}\)\(n=7\)\(0.1\text{ dB}\)\(n=9\)\(0.1\text{ dB}\) “>\(1.57340\) | \ (n=3\)\(0.2\text{ dB}\)\(n=5\)\(0.2\text{ dB}\)\(n=7\)\(0.2\text{ dB}\)\(n=9\)\(0.2\text{ dB}\) “>\(1.50016\) | \ (n=3\)\(1.0\text{ dB}\)\(n=5\)\(1.0\text{ dB}\)\(n=7\)\(1.0\text{ dB}\)\(n=9\)\(1.0\text{ dB}\) “>\(1.17352\) | \ (n=3\)\(3.0\text{ dB}\)\(n=5\)\(3.0\text{ dB}\)\(n=7\)\(3.0\text{ dB}\)\(n=9\)\(3.0\text{ dB}\) “>\(0.80381\) | \ (n=3\)\(\varepsilon =0.1\)\(n=5\)\(\varepsilon =0.1\)\(n=7\)\(\varepsilon =0.1\)\(n=9\)\(\varepsilon =0.1\) “>\(1.62196\) |
| \(g_{5}\) | \ (n=3\)\(0.01\text{ dB}\)\(n=5\)\(0.01\text{ dB}\)\(n=7\)\(0.01\text{ dB}\)\(n=9\)\(0.01\text{ dB}\) “>\(1.74813\) | \ (n=3\)\(0.1\text{ dB}\)\(n=5\)\(0.1\text{ dB}\)\(n=7\)\(0.1\text{ dB}\)\(n=9\)\(0.1\text{ dB}\) “>\(2.09667\) | \ (n=3\)\(0.2\text{ dB}\)\(n=5\)\(0.2\text{ dB}\)\(n=7\)\(0.2\text{ dB}\)\(n=9\)\(0.2\text{ dB}\) “>\(2.27566\) | \ (n=3\)\(1.0\text{ dB}\)\(n=5\)\(1.0\text{ dB}\)\(n=7\)\(1.0\text{ dB}\)\(n=9\)\(1.0\text{ dB}\) “>\(3.09364\) | \ (n=3\)\(3.0\text{ dB}\)\(n=5\)\(3.0\text{ dB}\)\(n=7\)\(3.0\text{ dB}\)\(n=9\)\(3.0\text{ dB}\) “>\(4.63898\) | \ (n=3\)\(\varepsilon =0.1\)\(n=5\)\(\varepsilon =0.1\)\(n=7\)\(\varepsilon =0.1\)\(n=9\)\(\varepsilon =0.1\) “>\(1.93981\) |
| \(g_{6}\) | \ (n=3\)\(0.01\text{ dB}\)\(n=5\)\(0.01\text{ dB}\)\(n=7\)\(0.01\text{ dB}\)\(n=9\)\(0.01\text{ dB}\) “>\(1.39242\) | \ (n=3\)\(0.1\text{ dB}\)\(n=5\)\(0.1\text{ dB}\)\(n=7\)\(0.1\text{ dB}\)\(n=9\)\(0.1\text{ dB}\) “>\(1.42281\) | \ (n=3\)\(0.2\text{ dB}\)\(n=5\)\(0.2\text{ dB}\)\(n=7\)\(0.2\text{ dB}\)\(n=9\)\(0.2\text{ dB}\) “>\(1.37820\) | \ (n=3\)\(1.0\text{ dB}\)\(n=5\)\(1.0\text{ dB}\)\(n=7\)\(1.0\text{ dB}\)\(n=9\)\(1.0\text{ dB}\) “>\(1.11151\) | \ (n=3\)\(3.0\text{ dB}\)\(n=5\)\(3.0\text{ dB}\)\(n=7\)\(3.0\text{ dB}\)\(n=9\)\(3.0\text{ dB}\) “>\(0.77220\) | \ (n=3\)\(\varepsilon =0.1\)\(n=5\)\(\varepsilon =0.1\)\(n=7\)\(\varepsilon =0.1\)\(n=9\)\(\varepsilon =0.1\) “>\(1.43678\) |
| \(g_{7}\) | \ (n=3\)\(0.01\text{ dB}\)\(n=5\)\(0.01\text{ dB}\)\(n=7\)\(0.01\text{ dB}\)\(n=9\)\(0.01\text{ dB}\) “>\(0.79694\) | \ (n=3\)\(0.1\text{ dB}\)\(n=5\)\(0.1\text{ dB}\)\(n=7\)\(0.1\text{ dB}\)\(n=9\)\(0.1\text{ dB}\) “>\(1.18118\) | \ (n=3\)\(0.2\text{ dB}\)\(n=5\)\(0.2\text{ dB}\)\(n=7\)\(0.2\text{ dB}\)\(n=9\)\(0.2\text{ dB}\) “>\(1.37226\) | \ (n=3\)\(1.0\text{ dB}\)\(n=5\)\(1.0\text{ dB}\)\(n=7\)\(1.0\text{ dB}\)\(n=9\)\(1.0\text{ dB}\) “>\(2.16656\) | \ (n=3\)\(3.0\text{ dB}\)\(n=5\)\(3.0\text{ dB}\)\(n=7\)\(3.0\text{ dB}\)\(n=9\)\(3.0\text{ dB}\) “>\(3.51852\) | \ (n=3\)\(\varepsilon =0.1\)\(n=5\)\(\varepsilon =0.1\)\(n=7\)\(\varepsilon =0.1\)\(n=9\)\(\varepsilon =0.1\) “>\(1.00794\) |
| Orden Ondulación | \(n=9\) | |||||
| \(0.01\text{ dB}\) | \(0.1\text{ dB}\) | \(0.2\text{ dB}\) | \(1.0\text{ dB}\) | \(3.0\text{ dB}\) | \(\varepsilon =0.1\) | |
| \(g_{1}\) | \ (n=3\)\(0.01\text{ dB}\)\(n=5\)\(0.01\text{ dB}\)\(n=7\)\(0.01\text{ dB}\)\(n=9\)\(0.01\text{ dB}\) “>\(0.81446\) | \ (n=3\)\(0.1\text{ dB}\)\(n=5\)\(0.1\text{ dB}\)\(n=7\)\(0.1\text{ dB}\)\(n=9\)\(0.1\text{ dB}\) “>\(1.19567\) | \ (n=3\)\(0.2\text{ dB}\)\(n=5\)\(0.2\text{ dB}\)\(n=7\)\(0.2\text{ dB}\)\(n=9\)\(0.2\text{ dB}\) “>\(1.38603\) | \ (n=3\)\(1.0\text{ dB}\)\(n=5\)\(1.0\text{ dB}\)\(n=7\)\(1.0\text{ dB}\)\(n=9\)\(1.0\text{ dB}\) “>\(2.17972\) | \ (n=3\)\(3.0\text{ dB}\)\(n=5\)\(3.0\text{ dB}\)\(n=7\)\(3.0\text{ dB}\)\(n=9\)\(3.0\text{ dB}\) “>\(3.53394\) | \ (n=3\)\(\varepsilon =0.1\)\(n=5\)\(\varepsilon =0.1\)\(n=7\)\(\varepsilon =0.1\)\(n=9\)\(\varepsilon =0.1\) “>\(1.02347\) |
| \(g_{2}\) | \ (n=3\)\(0.01\text{ dB}\)\(n=5\)\(0.01\text{ dB}\)\(n=7\)\(0.01\text{ dB}\)\(n=9\)\(0.01\text{ dB}\) “>\(1.42706\) | \ (n=3\)\(0.1\text{ dB}\)\(n=5\)\(0.1\text{ dB}\)\(n=7\)\(0.1\text{ dB}\)\(n=9\)\(0.1\text{ dB}\) “>\(1.44260\) | \ (n=3\)\(0.2\text{ dB}\)\(n=5\)\(0.2\text{ dB}\)\(n=7\)\(0.2\text{ dB}\)\(n=9\)\(0.2\text{ dB}\) “>\(1.39389\) | \ (n=3\)\(1.0\text{ dB}\)\(n=5\)\(1.0\text{ dB}\)\(n=7\)\(1.0\text{ dB}\)\(n=9\)\(1.0\text{ dB}\) “>\(1.11918\) | \ (n=3\)\(3.0\text{ dB}\)\(n=5\)\(3.0\text{ dB}\)\(n=7\)\(3.0\text{ dB}\)\(n=9\)\(3.0\text{ dB}\) “>\(0.76604\) | \ (n=3\)\(\varepsilon =0.1\)\(n=5\)\(\varepsilon =0.1\)\(n=7\)\(\varepsilon =0.1\)\(n=9\)\(\varepsilon =0.1\) “>\(1.46186\) |
| \(g_{3}\) | \ (n=3\)\(0.01\text{ dB}\)\(n=5\)\(0.01\text{ dB}\)\(n=7\)\(0.01\text{ dB}\)\(n=9\)\(0.01\text{ dB}\) “>\(1.80436\) | \ (n=3\)\(0.1\text{ dB}\)\(n=5\)\(0.1\text{ dB}\)\(n=7\)\(0.1\text{ dB}\)\(n=9\)\(0.1\text{ dB}\) “>\(2.13455\) | \ (n=3\)\(0.2\text{ dB}\)\(n=5\)\(0.2\text{ dB}\)\(n=7\)\(0.2\text{ dB}\)\(n=9\)\(0.2\text{ dB}\) “>\(2.30932\) | \ (n=3\)\(1.0\text{ dB}\)\(n=5\)\(1.0\text{ dB}\)\(n=7\)\(1.0\text{ dB}\)\(n=9\)\(1.0\text{ dB}\) “>\(3.12143\) | \ (n=3\)\(3.0\text{ dB}\)\(n=5\)\(3.0\text{ dB}\)\(n=7\)\(3.0\text{ dB}\)\(n=9\)\(3.0\text{ dB}\) “>\(4.66906\) | \ (n=3\)\(\varepsilon =0.1\)\(n=5\)\(\varepsilon =0.1\)\(n=7\)\(\varepsilon =0.1\)\(n=9\)\(\varepsilon =0.1\) “>\(1.98372\) |
| \(g_{4}\) | \ (n=3\)\(0.01\text{ dB}\)\(n=5\)\(0.01\text{ dB}\)\(n=7\)\(0.01\text{ dB}\)\(n=9\)\(0.01\text{ dB}\) “>\(1.71254\) | \ (n=3\)\(0.1\text{ dB}\)\(n=5\)\(0.1\text{ dB}\)\(n=7\)\(0.1\text{ dB}\)\(n=9\)\(0.1\text{ dB}\) “>\(1.61672\) | \ (n=3\)\(0.2\text{ dB}\)\(n=5\)\(0.2\text{ dB}\)\(n=7\)\(0.2\text{ dB}\)\(n=9\)\(0.2\text{ dB}\) “>\(1.53405\) | \ (n=3\)\(1.0\text{ dB}\)\(n=5\)\(1.0\text{ dB}\)\(n=7\)\(1.0\text{ dB}\)\(n=9\)\(1.0\text{ dB}\) “>\(1.18967\) | \ (n=3\)\(3.0\text{ dB}\)\(n=5\)\(3.0\text{ dB}\)\(n=7\)\(3.0\text{ dB}\)\(n=9\)\(3.0\text{ dB}\) “>\(0.81181\) | \ (n=3\)\(\varepsilon =0.1\)\(n=5\)\(\varepsilon =0.1\)\(n=7\)\(\varepsilon =0.1\)\(n=9\)\(\varepsilon =0.1\) “>\(1.67776\) |
| \(g_{5}\) | \ (n=3\)\(0.01\text{ dB}\)\(n=5\)\(0.01\text{ dB}\)\(n=7\)\(0.01\text{ dB}\)\(n=9\)\(0.01\text{ dB}\) “>\(1.90579\) | \ (n=3\)\(0.1\text{ dB}\)\(n=5\)\(0.1\text{ dB}\)\(n=7\)\(0.1\text{ dB}\)\(n=9\)\(0.1\text{ dB}\) “>\(2.20537\) | \ (n=3\)\(0.2\text{ dB}\)\(n=5\)\(0.2\text{ dB}\)\(n=7\)\(0.2\text{ dB}\)\(n=9\)\(0.2\text{ dB}\) “>\(2.37280\) | \ (n=3\)\(1.0\text{ dB}\)\(n=5\)\(1.0\text{ dB}\)\(n=7\)\(1.0\text{ dB}\)\(n=9\)\(1.0\text{ dB}\) “>\(3.17463\) | \ (n=3\)\(3.0\text{ dB}\)\(n=5\)\(3.0\text{ dB}\)\(n=7\)\(3.0\text{ dB}\)\(n=9\)\(3.0\text{ dB}\) “>\(4.72701\) | \ (n=3\)\(\varepsilon =0.1\)\(n=5\)\(\varepsilon =0.1\)\(n=7\)\(\varepsilon =0.1\)\(n=9\)\(\varepsilon =0.1\) “>\(2.06485\) |
| \(g_{6}\) | \ (n=3\)\(0.01\text{ dB}\)\(n=5\)\(0.01\text{ dB}\)\(n=7\)\(0.01\text{ dB}\)\(n=9\)\(0.01\text{ dB}\) “>\(1.71254\) | \ (n=3\)\(0.1\text{ dB}\)\(n=5\)\(0.1\text{ dB}\)\(n=7\)\(0.1\text{ dB}\)\(n=9\)\(0.1\text{ dB}\) “>\(1.61672\) | \ (n=3\)\(0.2\text{ dB}\)\(n=5\)\(0.2\text{ dB}\)\(n=7\)\(0.2\text{ dB}\)\(n=9\)\(0.2\text{ dB}\) “>\(1.53405\) | \ (n=3\)\(1.0\text{ dB}\)\(n=5\)\(1.0\text{ dB}\)\(n=7\)\(1.0\text{ dB}\)\(n=9\)\(1.0\text{ dB}\) “>\(1.18967\) | \ (n=3\)\(3.0\text{ dB}\)\(n=5\)\(3.0\text{ dB}\)\(n=7\)\(3.0\text{ dB}\)\(n=9\)\(3.0\text{ dB}\) “>\(0.81181\) | \ (n=3\)\(\varepsilon =0.1\)\(n=5\)\(\varepsilon =0.1\)\(n=7\)\(\varepsilon =0.1\)\(n=9\)\(\varepsilon =0.1\) “>\(1.67776\) |
| \(g_{7}\) | \ (n=3\)\(0.01\text{ dB}\)\(n=5\)\(0.01\text{ dB}\)\(n=7\)\(0.01\text{ dB}\)\(n=9\)\(0.01\text{ dB}\) “>\(1.80436\) | \ (n=3\)\(0.1\text{ dB}\)\(n=5\)\(0.1\text{ dB}\)\(n=7\)\(0.1\text{ dB}\)\(n=9\)\(0.1\text{ dB}\) “>\(2.13455\) | \ (n=3\)\(0.2\text{ dB}\)\(n=5\)\(0.2\text{ dB}\)\(n=7\)\(0.2\text{ dB}\)\(n=9\)\(0.2\text{ dB}\) “>\(2.30932\) | \ (n=3\)\(1.0\text{ dB}\)\(n=5\)\(1.0\text{ dB}\)\(n=7\)\(1.0\text{ dB}\)\(n=9\)\(1.0\text{ dB}\) “>\(3.12143\) | \ (n=3\)\(3.0\text{ dB}\)\(n=5\)\(3.0\text{ dB}\)\(n=7\)\(3.0\text{ dB}\)\(n=9\)\(3.0\text{ dB}\) “>\(4.66906\) | \ (n=3\)\(\varepsilon =0.1\)\(n=5\)\(\varepsilon =0.1\)\(n=7\)\(\varepsilon =0.1\)\(n=9\)\(\varepsilon =0.1\) “>\(1.98372\) |
| \(g_{8}\) | \ (n=3\)\(0.01\text{ dB}\)\(n=5\)\(0.01\text{ dB}\)\(n=7\)\(0.01\text{ dB}\)\(n=9\)\(0.01\text{ dB}\) “>\(1.42706\) | \ (n=3\)\(0.1\text{ dB}\)\(n=5\)\(0.1\text{ dB}\)\(n=7\)\(0.1\text{ dB}\)\(n=9\)\(0.1\text{ dB}\) “>\(1.44260\) | \ (n=3\)\(0.2\text{ dB}\)\(n=5\)\(0.2\text{ dB}\)\(n=7\)\(0.2\text{ dB}\)\(n=9\)\(0.2\text{ dB}\) “>\(1.39389\) | \ (n=3\)\(1.0\text{ dB}\)\(n=5\)\(1.0\text{ dB}\)\(n=7\)\(1.0\text{ dB}\)\(n=9\)\(1.0\text{ dB}\) “>\(1.11918\) | \ (n=3\)\(3.0\text{ dB}\)\(n=5\)\(3.0\text{ dB}\)\(n=7\)\(3.0\text{ dB}\)\(n=9\)\(3.0\text{ dB}\) “>\(0.76604\) | \ (n=3\)\(\varepsilon =0.1\)\(n=5\)\(\varepsilon =0.1\)\(n=7\)\(\varepsilon =0.1\)\(n=9\)\(\varepsilon =0.1\) “>\(1.46186\) |
| \(g_{9}\) | \ (n=3\)\(0.01\text{ dB}\)\(n=5\)\(0.01\text{ dB}\)\(n=7\)\(0.01\text{ dB}\)\(n=9\)\(0.01\text{ dB}\) “>\(0.81446\) | \ (n=3\)\(0.1\text{ dB}\)\(n=5\)\(0.1\text{ dB}\)\(n=7\)\(0.1\text{ dB}\)\(n=9\)\(0.1\text{ dB}\) “>\(1.19567\) | \ (n=3\)\(0.2\text{ dB}\)\(n=5\)\(0.2\text{ dB}\)\(n=7\)\(0.2\text{ dB}\)\(n=9\)\(0.2\text{ dB}\) “>\(1.38603\) | \ (n=3\)\(1.0\text{ dB}\)\(n=5\)\(1.0\text{ dB}\)\(n=7\)\(1.0\text{ dB}\)\(n=9\)\(1.0\text{ dB}\) “>\(2.17972\) | \ (n=3\)\(3.0\text{ dB}\)\(n=5\)\(3.0\text{ dB}\)\(n=7\)\(3.0\text{ dB}\)\(n=9\)\(3.0\text{ dB}\) “>\(3.53394\) | \ (n=3\)\(\varepsilon =0.1\)\(n=5\)\(\varepsilon =0.1\)\(n=7\)\(\varepsilon =0.1\)\(n=9\)\(\varepsilon =0.1\) “>\(1.02347\) |
Tabla\(\PageIndex{2}\): Coeficientes de un filtro prototipo de paso bajo Chebyshev normalizados a una frecuencia de esquina de radianes\(\omega_{0} = 1\text{ rad/s}\) y una impedancia\(1\:\Omega\) del sistema (i.e.,\(g_{0} = 1 = g_{n+1}\)). El factor de ondulación\(\varepsilon\),, está relacionado con la ondulación en decibelios por Ecuación\(\eqref{eq:13}\) (por ejemplo,\(\varepsilon = 0.1\) es una ondulación de\(0.0432\text{ dB}\)). (Obsérvese que\(\omega_{0}\) es la frecuencia de radianes a la que la respuesta de transmisión de un filtro de Chebyshev es descendente por la ondulación, ver Figura 2.4.2.)
mientras que para una función de grado par (es decir,\(n\) es par) existe un desajuste de valor
\[\label{eq:15}|T(0)|^{2}=\frac{4R_{L}}{(R_{L}+1)^{2}}=\frac{1}{1+\varepsilon^{2}} \]
para que
\[\label{eq:16}R_{L}=g_{n+1}=\left[\varepsilon +\sqrt{(1+\varepsilon^{2})}\right]^{2} \]
Los coeficientes de varios filtros prototipo de paso bajo de Chebyshev con diferentes niveles de ondulación y órdenes impares hasta el noveno orden se dan en la Tabla\(\PageIndex{2}\).
2.7.3 Resumen
Un filtro Butterworth tiene una respuesta monótona sin ondulación, pero una transición relativamente lenta de la banda de paso a la banda de parada. Un filtro Chebyshev tiene una transición rápida pero tiene ondulación en la banda de parada o banda de paso. Los filtros Butterworth y Chebyshev son casos especiales de filtros elípticos, que también se llaman filtros Cauer. En general, un filtro elíptico tiene ondulación tanto en la banda de detención como en la banda de paso. El nivel de la ondulación se puede seleccionar
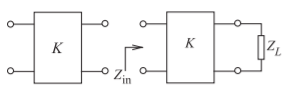
Figura\(\PageIndex{4}\): Inversor de impedancia (de impedancia K en ohmios): (a) representado como un puerto de dos; y (b) el de dos puertos terminado en una carga.
independientemente en cada banda. Con cero ondulación en la banda de detención, pero ondulación en la banda de paso, un filtro elíptico se convierte en un filtro Chebyshev Tipo I. Con cero ondulación en la banda de paso, pero ondulación en la banda de detención, un filtro elíptico se convierte en un filtro Chebyshev Tipo II. Sin ondulación en ninguna de las bandas, el filtro elíptico se convierte en un filtro Butterworth. Con ondulación tanto en la banda de paso como en la banda de parada, la transición entre la banda de paso y la banda de detención se puede hacer más abrupta o, alternativamente, aumentar la tolerancia a las variaciones de componentes.
Otro tipo de filtro es el filtro Bessel que tiene un retardo de grupo máximo plano en la banda de paso, lo que significa que la respuesta de fase tiene linealidad máxima a través de la banda de paso. El filtro Legendre (también conocido como el filtro “L” óptimo) tiene una alta tasa de transición de banda de paso a banda de parada para un orden de filtro dado, y también tiene una respuesta de frecuencia monótona (es decir, sin ondulación). Es un compromiso entre el filtro Butterworth, con respuesta de frecuencia monótona pero transición más lenta y el filtro Chebyshev, que tiene una transición más rápida pero ondulaciones en la respuesta de frecuencia.
Discusiones más profundas de una gran clase de filtros junto con tablas de coeficientes y fórmulas de coeficientes están disponibles en Matthaei et al. [1], Hunter [3], Daniels [8], Lutovac et al. [9], y en la mayoría de los otros libros dedicados exclusivamente a filtros de microondas.

