2.15: Topologías de filtro paso banda

Última actualización
Guardar como PDF

Page ID: 85172

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

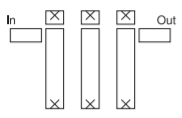
Figura\(\PageIndex{1}\): Disposición de microcinta de un filtro combline de tercer orden basado en líneas acopladas. Cada una de las líneas verticales de microcinta forma un resonador con los condensadores de separación superior. Los condensadores de separación de entrada y salida proporcionan una adaptación de impedancia.

La estructura esencial de un filtro de paso de banda comprende resonadores que están acoplados entre sí. Se han desplegado una gran cantidad de arquitecturas de filtro basadas en este concepto. En la Figura se muestra un filtro de línea acoplada paralela (PCL) llamado filtro de línea combline\(\PageIndex{1}\). Aquí las líneas de microcinta forman el resonador y el acoplamiento de líneas paralelas proporciona el acoplamiento interresonador. En la Figura\(\PageIndex{2}\) [22] se muestra una variación en un filtro con resonadores PCL. Este filtro utiliza resonadores de microbanda acoplados a bordes que son\(\lambda /2\) largos (en la frecuencia central). La figura\(\PageIndex{3}\) muestra otra topología de filtro de paso de banda distribuida que utiliza resonadores de microbanda acoplados en extremos. Es decir, los huecos proporcionan el acoplamiento interresonador. Todos los filtros pasabanda de línea de transmisión tienen bandas de paso espurias [23, 24, 25]. La causa raíz de las respuestas espurias deriva de la transformación de los\(LC\) resonadores paralelos en su forma de línea de transmisión.

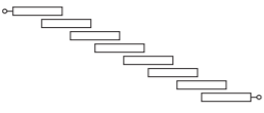
Figura\(\PageIndex{2}\): Disposición de microcinta de un filtro de paso de banda acoplado en paralelo.

Figura\(\PageIndex{3}\): Disposición general de microcinta para un filtro de paso de banda acoplado de extremo (huecos de acoplamiento en serie entre elementos resonadores rectos en cascada).

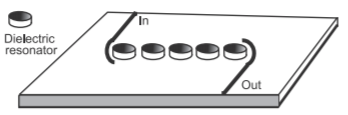
Figura\(\PageIndex{4}\): Una configuración de filtro pasabanda de resonador dieléctrico acoplado a microcinta.

Un filtro de paso de banda basado en resonador dieléctrico se muestra en la Figura\(\PageIndex{4}\) [26]. Aquí los discos son los resonadores pasabanda y están acoplados y los campos evanescentes fuera de los discos proporcionan el acoplamiento interresonador. Los discos mostrados son cilindros de material de alta permitividad (típicamente que tienen una permitividad relativa de\(500–85000\)) con una pared magnética aproximada en la superficie cilíndrica del puck. Así, el puck resuena cuando su diámetro es aproximadamente\(\lambda /2\). \(^{1}\)

Con todos estos filtros el acoplamiento interresonador funciona como un inversor. Así, la unidad funcional básica de los filtros pasabanda es la estructura del resonador acoplado que se muestra en la Figura 2.14.1 (b).

Notas al pie

[1] Se desarrolla una mejor estimación a partir de los ceros de las funciones de Bessel, ya que los campos dentro de los discos tienen una dependencia de la función de Bessel (esta es la forma de la solución de la ecuación de onda en coordenadas cilíndricas).