3.8: Ejercicios

1. En la Figura 3.2.11 se muestra una sección paralela de línea acoplada. La impedancia de modo par de la línea acoplada es\(60\:\Omega\) y la impedancia de modo impares es\(40\:\Omega\). La sección PCL es\(\lambda/4\) larga en la frecuencia central de la sección.
   1. ¿Cuál es la impedancia del sistema\(Z_{0S}\)?
   2. ¿Qué es\(Z_{01}\)?
   3. ¿Qué es\(Z_{02}\)?
   4. ¿Qué es\(n\)?
   5. ¿Cuál es la impedancia de entrada en el puerto\(2\) si\(4\) el puerto se termina en\(50\:\Omega\)? Calcule esto a la frecuencia a la que la sección es\(\lambda /4\) larga.
2. En la Figura 3.2.11 se muestra una sección paralela de línea acoplada de un filtro. La impedancia de modo par de la línea acoplada es\(65\:\Omega\) y la impedancia de modo impares es\(35\:\Omega\). La sección PCL es\(\lambda/4\) larga en la frecuencia central,\(f_{0}\), de la sección y Port\(4\) se termina en\(50\:\Omega\). [Pista: Considere las\(Z_{02}\) líneas\(Z_{01}\) y. Ellos son\(\lambda/4\) largos en\(f_{0}\). Quizás se haya proporcionado más información de la que necesita.]
   1. ¿Cuál es la impedancia de entrada para\(f_{0}\) buscar en Port\(2\)?
   2. ¿Cuál es la impedancia de entrada para\(3f_{0}\) buscar en Port\(2\)?
   3. ¿Cuál es la impedancia de entrada en CC buscando en Port\(2\)?
3. En la Figura 3.2.12 se muestra una sección interdigital de línea acoplada de un filtro. La impedancia de modo par de la línea acoplada es\(65\:\Omega\) y la impedancia de modo impares es\(45\:\Omega\). La sección PCL es\(\lambda /4\) larga en la frecuencia central del filtro.
   1. ¿Cuál es la impedancia del sistema\(Z_{0S}\)?
   2. ¿Qué es\(Z_{01}\)?
   3. ¿Qué es\(Z_{02}\)?
   4. ¿Qué es\(n\)?
   5. ¿Cuál es la impedancia de entrada en el puerto\(2\) si\(4\) el puerto se termina en\(50\:\Omega\)? Calcule esto en la frecuencia central del filtro.
4. En la Figura 3.2.12 se muestra una sección interdigital de línea acoplada de un filtro. La impedancia de modo par de la línea acoplada es\(65\:\Omega\) y la impedancia de modo impares es\(35\:\Omega\). La sección PCL es\(\lambda /4\) larga en la frecuencia central\(f_{0}\),, del filtro y Port\(4\) se termina en\(50\:\Omega\). [Pista: Considere las\(Z_{02}\) líneas\(Z_{01}\) y. Ellos son\(\lambda /4\) largos en\(f_{0}\). Quizás se haya proporcionado más información de la que necesita.]
   1. ¿Cuál es la impedancia de entrada para\(f_{0}\) buscar en Port\(2\)?
   2. ¿Cuál es la impedancia de entrada para\(3f_{0}\) buscar en Port\(2\)?
   3. ¿Cuál es la impedancia de entrada para\(2f_{0}\) buscar en Port\(2\)?
5. En la Figura 3.2.13 se muestra una sección de combline de un filtro. La impedancia de modo par de la línea acoplada es\(60\:\Omega\) y la impedancia de modo impares es\(40\:\Omega\). La sección PCL es\(\lambda /4\) larga en la frecuencia central del filtro.
   1. ¿Cuál es la impedancia del sistema\(Z_{0S}\)?
   2. ¿Qué es\(Z_{01}\)?
   3. ¿Qué es\(Z_{02}\)?
   4. ¿Qué es\(n\)?
   5. ¿Cuál es la impedancia de entrada en el puerto\(1\) si\(2\) el puerto se termina en\(50\:\Omega\)?
6. En la Figura 3.2.13 se muestra una sección de combline de un filtro. La impedancia de modo par de la línea acoplada es\(55\:\Omega\) y la impedancia de modo impares es\(35\:\Omega\). La sección PCL es\(\lambda /4\) larga en la frecuencia central\(f_{0}\),, del filtro y Port\(2\) se termina en\(50\:\Omega\). [Pista: Considere las\(Z_{02}\) líneas\(Z_{01}\) y. Ellos son\(\lambda /4\) largos en\(f_{0}\). Quizás se haya proporcionado más información de la que necesita.]
   1. ¿Cuál es la impedancia de entrada para\(f_{0}\) buscar en Port\(1\)?
   2. ¿Cuál es la impedancia de entrada para\(3f_{0}\) buscar en Port\(1\)?
   3. ¿Cuál es la impedancia de entrada para\(2f_{0}\) buscar en Port\(1\)?

Ejercicios\(7\) para\(30\) cubrir el diseño de un filtro combinado Butterworth de tercer orden. La mayoría de los ejercicios comienzan a partir de la solución del ejercicio anterior. Generalmente tu respuesta para cada ejercicio debe corresponder al punto de partida previsto para el siguiente paso en el diseño. Debes mostrar tu trabajo detallado.

7. Dibuje y derive los valores del prototipo de filtro de paso bajo de un filtro prototipo de paso bajo Butterworth de tercer orden con una frecuencia de esquina de\(1\text{ rad/s}\) y en un\(1\:\Omega\) sistema. Muestre y describa su trabajo. [Parallels Paso 1 en la Sección 3.4.]
8. El prototipo de paso bajo de un filtro Butterworth de tercer orden con una frecuencia de esquina de\(1\text{ rad/s}\) y en un\(1\:\Omega\) sistema se muestra en la Figura\(\PageIndex{1}\) (a), donde\(C_{1} = 1\text{ F},\: L_{2} = 2\text{ H}\), y\(C_{3} = 1\text{ F}\). Transforme este circuito en un filtro de paso de banda de elementos agrupados con frecuencias de esquina de\(f_{1} = 878.42\text{ MHz}\) y\(f_{2} = 1.1384\text{ GHz}\), y en un\(50\:\Omega\) sistema. Dibuja y deriva los valores del filtro pasabanda.
9. El prototipo de paso bajo de un filtro Butterworth de tercer orden con una frecuencia de esquina de\(1\text{ rad/s}\) y en un\(1\:\Omega\) sistema se muestra en la Figura\(\PageIndex{1}\) (a), donde\(C_{1} = 1\text{ F},\: L_{2} = 2\text{ H}\), y\(C_{3} = 1\text{ F}\). Reemplace el elemento serie usando un elemento de derivación e inversores. Este debe tener propiedades eléctricas idénticas a las del circuito de la Figura\(\PageIndex{1}\) (a). [Parallels Paso 2 en la Sección 3.4.]
10. El prototipo de paso bajo de un filtro Butterworth de tercer orden con una frecuencia de esquina de\(1\text{ rad/s}\) y en un\(1\:\Omega\) sistema se muestra en la Figura\(\PageIndex{1}\) (a), donde\(C_{1} = 1\text{ F},\: L_{2} = 2\text{ H}\), y\(C_{3} = 1\text{ F}\). Reemplace el elemento serie usando un elemento de derivación e inversor (es) y dibuje y derive los valores del nuevo prototipo ahora con una frecuencia de esquina de\(1\text{ Hz}\). Este debe tener propiedades eléctricas idénticas a las del circuito de la Figura\(\PageIndex{1}\) (a). [Parallels Paso 2 en la Sección 3.4.]
11. Considere eliminar el transformador en la Figura\(\PageIndex{1}\) (b).
    1. ¿Qué efecto tiene esto en las propiedades del filtro de paso bajo?
    2. Dibujar y derivar los valores del nuevo prototipo sin el transformador.
12. Derive el prototipo de filtro de paso de banda de un filtro de paso de banda de tercer orden con frecuencias de esquina de\(f_{1} = 878.42\text{ MHz}\) y\(f_{2} = 1.1384\text{ GHz}\). Basarlo en el prototipo de paso bajo Butterworth de\(1\:\Omega\) tercer orden que se muestra en la Figura\(\PageIndex{1}\) (c) con\(C_{1} = C_{3} = 1\text{ F}\) y\(C_{2} = 2\text{ F}\).
    1. ¿Cuál es la frecuencia central del filtro de paso de banda?
    2. ¿Cuál es el ancho de banda fraccional?
    3. Primero considere un\(1\:\Omega\) sistema (es decir, las resistencias de fuente y carga son\(1\:\Omega\)). Use dos inversores de\(1\:\Omega\) impedancia, pero no use stubs. Dibujar y derivar los valores del nuevo prototipo. [Parallels Paso 3 en la Sección 3.4.]
    4. Transformar el prototipo desarrollado en (a) en un\(50\:\Omega\) sistema (es decir, las resistencias de fuente y carga son\(50\:\Omega\)). Dibujar y derivar los valores del nuevo prototipo. [Parallels Paso 4 en la Sección 3.4.]
13. Considera un talón cortocircuitado que es resonante a la frecuencia\(f_{r}\).
    1. ¿Cuál es la impedancia de entrada del stub en resonancia (esto debe tomarse como la primera resonancia)?
    2. En cuanto a longitudes de onda, ¿cuánto tiempo está el stub\(f_{r}\)?
    3. En cuanto a longitudes de onda, ¿cuánto tiempo está el stub\(\frac{1}{2}f_{r}\)?
14. Considera un talón de circuito abierto que es resonante a la frecuencia\(f_{r}\).
    1. ¿Cuál es la impedancia de entrada del stub en resonancia (esto debe tomarse como la primera resonancia)?
    2. En cuanto a longitudes de onda, ¿cuánto tiempo está el stub\(f_{r}\)?
    3. En cuanto a longitudes de onda, ¿cuánto tiempo está el stub\(\frac{1}{2}f_{r}\)?
15. Considera un condensador\(C\).
    1. ¿Cuál es la admitancia con respecto a la frecuencia de radianes del condensador a la frecuencia\(f_{0} =\omega_{0}/2\pi\)?
    2. ¿Cuál es la derivada de la admitancia del condensador con respecto a la frecuencia de radianes del condensador del resonador a\(f_{0}\)?
16. Un resonador que comprende un condensador\(C\) en paralelo con un inductor\(L\) es resonante a una frecuencia\(f_{0}\).
    1. ¿Cuál es la admisión del resonador\(f_{0}\)?
    2. ¿Cuál es la derivada con respecto a la frecuencia de radianes de la admitancia del resonador a\(f_{0}\)?
17. Considera un talón cortocircuitado que es resonante a la frecuencia\(f_{r} = 2f_{0}\).
    1. En cuanto a longitudes de onda, ¿cuánto tiempo está el stub\(f_{r}\)?
    2. En cuanto a longitudes de onda, ¿cuánto tiempo está el stub\(f_{0}\)?
    3. ¿En qué se encuentra la admisión del talón\(f_{0}\)?
    4. ¿Cuál es la derivada con respecto a la frecuencia radianes de la admisión del trozo a\(f_{0}\)?
18. Un resonador de elementos grumados consiste en un condensador paralelo\(C_{1}^{♯} = 12.2427\text{ pF}\) y un inductor\(L_{1}^{♯} = 2.06901\text{ nH}\). Derive un resonador equivalente que comprende un condensador en paralelo con un trozo cortocircuitado que es resonante a la frecuencia\(f_{r} = 2f_{0}\). El nuevo resonador debe tener la misma admitancia en\(f_{0} = 1\text{ GHz}\) que el resonador original y la derivada de la admitancia debe ser la misma en\(f_{0}\) para ambos resonadores. Dibuja y deriva los valores del nuevo resonador. [Parallels Paso 5 en la Sección 3.4.]
19. El prototipo de un filtro de paso de banda Butterworth de\(50\:\Omega\) tercer orden se muestra en la Figura\(\PageIndex{1}\) (e). El filtro tiene una frecuencia central de\(f_{0} = 1\text{ GHz}\), dónde\(C_{1}^{♯} = C_{3}^{♯} = 12.2427\text{ pF}\)\(L_{1}^{♯} = L_{3}^{♯} = 2.06901\text{ nH},\: C_{2}^{♯} = 24.4854\text{ pF}\), y\(L_{2}^{♯} = 1.03451\text{ nH}\). Reemplace cada uno de los tres resonadores de elementos grumados por un resonador que consiste en un solo condensador y un trozo en cortocircuito. Cada uno de los nuevos resonadores debe tener la misma admitancia en\(f_{0}\) que el resonador original que reemplazó y la derivada con respecto a la frecuencia de las admitancias de cada uno de los resonadores originales y de reemplazo debe ser la misma en\(f_{0}\). Dibuja y deriva los valores del nuevo prototipo de filtro. [Parallels Paso 5 en la Sección 3.4.]
20. Un trozo cortocircuitado tiene una impedancia característica de\(Z_{01} = 75\:\Omega\) y es resonante a la frecuencia\(f_{r} = 2f_{0}\).
    1. ¿Cuál es la impedancia de entrada del stub\(f_{r}\)?
    2. ¿Cuál es la impedancia de entrada del stub\(f_{0}\)?
21. El prototipo de un filtro de paso de banda Butterworth de\(50\:\Omega\) tercer orden se muestra en la Figura\(\PageIndex{1}\) (f). El filtro tiene una frecuencia central de\(f_{0} = 1\text{ GHz}\), donde\(C_{1}′′ = C_{3}′′ = 9.52443\text{ pF},\: Z_{01} = Z_{03} = 16.7102\:\Omega,\: C_{2}′′ = 19.0489\text{ pF},\: Z_{02} = 8.35509\:\Omega\). La frecuencia resonante de cada uno de los talones es\(f_{r} = 2f_{0}\). [Parallels Paso 6 en la Sección 3.4.]
    1. ¿Cuál es la impedancia\(f_{0}\) de entrada del stub con impedancia característica\(Z_{01}\)?
    2. Transformar el prototipo para que cada stub tenga la impedancia característica\(Z_{01}\).
22. Un inversor de impedancia tiene una impedancia característica de\(50\:\Omega\). Desarrollar el circuito equivalente de elementos grumados del inversor. El circuito equivalente debe tener tres impedancias agrupadas. Dibuja y deriva los valores del circuito equivalente.
23. Un inversor de impedancia tiene una impedancia característica de\(60\:\Omega\). Desarrollar el circuito equivalente de elementos grumados del inversor en\(1\text{ GHz}\). El circuito equivalente debe tener tres elementos agrupados. Dibuje y derive los valores del circuito equivalente con los valores de inductor y condensador.
24. El prototipo de un filtro de paso de banda Butterworth de\(50\:\Omega\) tercer orden se muestra en la Figura\(\PageIndex{1}\) (g). El filtro tiene una frecuencia central de\(f_{0} = 1\text{ GHz}\), dónde\(C_{1}′′ = C_{2}′′′ = C_{3}′′ = 9.52443\text{ pF},\: Z_{01} = Z_{02}′ = Z_{03} = 16.7102\:\Omega\), y\(Z_{y} = 70.7107\:\Omega\). La frecuencia resonante de los talones es\(f_{r} = 2f_{0}\). Dibuje y derive los valores del prototipo de filtro con los inversores reemplazados por stubs cortocircuitados resonantes en\(f_{r}\). [Parallels Paso 7 en la Sección 3.4.]
25. El prototipo de un filtro de paso de banda Butterworth de\(50\:\Omega\) tercer orden se muestra en la Figura\(\PageIndex{2}\) (h). El filtro tiene una frecuencia central de\(f_{0} = 1\text{ GHz}\), dónde\(C_{1}′′= C_{3}′′ = 9.52443\text{ pF},\: Z_{01}′ = Z_{03}′ = 21.8811\:\Omega,\: C_{2}′′′ = 9.52443\text{ pF},\: Z_{02}′′ = 31.6862\:\Omega\), y\(Z_{012} = Z_{023} = 70.7107\:\Omega\). La frecuencia resonante de los talones es\(f_{r} = 2f_{0}\). Las impedancias características\(Z_{01}′,\: Z_{02}′′,\) y\(Z_{03}′\) son demasiado bajas para ser realizadas en microstrip y por lo tanto necesitan ser escaladas a una impedancia microstrip más razonable (digamos entre\(30\:\Omega\) y\(80\:\Omega\)). Escala el talón medio,\(Z_{02}′′\) a\(80\:\Omega\). Esto alejará las impedancias de fuente y carga\(50\:\Omega\), pero esto se puede acomodar en un último paso. [Parallels Paso 8 en la Sección 3.4.]
26. El prototipo de un filtro de paso de banda Butterworth de tercer orden se muestra en la Figura\(\PageIndex{2}\) (i). El filtro tiene una frecuencia central de\(f_{0} = 1\text{ GHz}\), dónde\(R_{S} = R_{L} = 126.238\:\Omega,\: C_{t1} = C_{t2} = C_{t3} = 3.77241\text{ pF},\: Z_{0t1} = Z_{0t3} = 55.2444\:\Omega,\: Z_{0t2} = 80\:\Omega\), y\(Z_{0t12} = Z_{0t23} = 178.528\:\Omega\). La frecuencia resonante de los talones es\(f_{r} = 2f_{0}\). Incorporar un inversor en la entrada y en la salida del filtro para que interactue con impedancias de\(50\:\Omega\) fuente y carga. Dibujar y derivar los valores del nuevo prototipo. [Parallels Paso 9 en la Sección 3.4.]
27. El prototipo de un filtro de paso de banda Butterworth de tercer orden se muestra en la Figura\(\PageIndex{2}\) (j). El filtro tiene una frecuencia central de\(f_{0} = 1\text{ GHz}\), donde los inversores de impedancia tienen impedancias\(Z_{1} = Z_{2} = 79.4475\:\Omega,\: C_{t1}= C_{t2} = C_{t3} = 3.77241\text{ pF},\: Z_{0t2}′′ = 80\:\Omega,\: Z_{0t1} = Z_{0t3} = 55.244\:\Omega\), y\(Z_{0t12} = Z_{0t23} = 178.5275\:\Omega\). La frecuencia resonante de los talones es\(f_{r} = 2f_{0}\). Incorporar un inversor en la entrada y en la salida del filtro para que interactue con las impedancias de\(50\:\Omega\) fuente y carga. Dibujar y derivar los valores del nuevo prototipo. Date cuenta de que cada uno de los inversores de impedancia utiliza una red de dos condensadores señalando que un lado de los inversores es una resistencia. Tenga en cuenta que uno de los valores de condensador en cada red será negativo. [Parallels Paso 9 en la Sección 3.4.]
28. El prototipo de un filtro de paso de banda Butterworth de tercer orden se muestra en la Figura\(\PageIndex{2}\) (k). El filtro tiene una frecuencia central de\(f_{0} = 1\text{ GHz}\) donde\(C_{b} = 2.57780\text{ pF},\: C_{1} = C_{3} = 2.21562\text{ pF},\: Z_{0t1} = Z_{0t3} = 55.2444\:\Omega,\: Z_{0t2}′′ = 80\:\Omega,\: Z_{0t12} = Z_{0t23} = 178.5275\:\Omega,\: C_{t2} = 3.77241\text{ pF}\). Dibuje la disposición física del circuito asumiendo que se utilizarán capacitores de elementos grumados. No es necesario desarrollar las dimensiones de las líneas de microcinta. [Parallels Paso 9 en la Sección 3.4.]
29. Diseñe un prototipo de filtro de paso de banda máximo plano de tercer orden en un\(50\:\Omega\) sistema centrado en\(1\text{ GHz}\) con un\(10\%\) ancho de banda. El prototipo de paso bajo de un filtro plano máximo de tercer orden se muestra en la Figura 2.6.3. El problema será paralelo al desarrollo en la Sección 3.4 y el resultado final de este desarrollo será un filtro prototipo pasabanda con la forma de la de la Figura 3.4.14. Tenga en cuenta que habrá diferencias ya que el filtro es de un tipo diferente.
    1. Convierta el filtro de paso bajo prototipo en un filtro de paso bajo con inversores y condensadores solamente; es decir, retire los inductores en serie.
    2. Escala el filtro para tomar la frecuencia de esquina de\(1\text{ rad/s}\) a\(1\text{ GHz}\).
    3. Transforme el filtro de paso bajo en un filtro de paso de banda. Es decir, reemplace cada condensador de derivación por una\(LC\) red paralela. Este paso establecerá el ancho de banda del filtro.
    4. Transformar la impedancia del sistema del filtro de\(1\) a\(50\:\Omega\).
    5. Reemplace los\(LC\) circuitos paralelos por stubs cortocircuitados en paralelo con condensadores agrupados. (El circuito ahora estará en una forma similar a la de la Figura 3.4.10.)
    6. Para cada inversor, se deriva el circuito equivalente de tres elementos en forma de grumos como en la Figura 2.8.6. No actualice todavía el prototipo del filtro, sino que dibuje y etiquete los circuitos equivalentes a elementos grumados de cada inversor.
30. Un puerto de dos que consiste en tres stubs cortocircuitados en una estructura Pi con los stubs de derivación teniendo una impedancia característica de\(55.2444\:\Omega\) y el stub serie tiene una impedancia característica de\(178.5275\:\Omega\). La frecuencia de operación es\(f_{0} = 1\text{ GHz}\) y la frecuencia resonante de los stubs es\(f_{r} = 2f_{0}\). El sustrato tiene un espesor de\(500\:\mu\text{m}\) y una permitividad relativa\(\varepsilon_{r}\) de\(10\).
    1. Dibuje el inversor.
    2. Dibuje el par de líneas acopladas en configuración de combline y dibuje dos modelos de circuito equivalentes del combline. Tenga en cuenta que las líneas acopladas son\(\lambda /8\) largas en\(f_{0}\). Calcula los valores de los elementos en tus modelos equivalentes.
    3. Calcular dos valores para la impedancia del sistema. Tome la impedancia del sistema como la media geométrica de estos dos valores.
    4. Calcular la impedancia de modo impar de las líneas acopladas. (Use\(50\:\Omega\) si no pudo resolver la Parte (c).)
    5. Calcular la impedancia de modo par de las líneas acopladas. (Use\(50:\Omega\) si no pudo resolver la Parte (c).)
    6. Calcular el ancho y separación de las líneas acopladas. El uso puede querer usar las Figuras 5-10 a 5-13 y/o las Tablas 5-2 y 5-3 de [29]. Además, es posible que necesites interpolar. Usa las tablas o figuras aunque la impedancia de tu sistema no sea\(50\:\Omega\).
    7. ¿Cuál es la permitividad efectiva del modo par?
    8. ¿Cuál es la permitividad efectiva del modo impar?
    9. Determinar la longitud de las líneas acopladas tomando la permitividad efectiva promedio como la media geométrica de los valores de modo par e impares.
31. El prototipo de un filtro de paso de banda Butterworth de tercer orden se muestra en la Figura\(\PageIndex{2}\) (k). El filtro tiene una frecuencia central de\(f_{0} = 1\text{ GHz}\), donde\(C_{b} = 2.57780\text{ pF},\: C_{1} = C_{3} = 2.21562\text{ pF},\)\(Z_{0t1} = Z_{0t3} = 55.2444\:\Omega,\)\(Z_{0t2}′′ = 80\:\Omega,\)\(Z_{0t12} = Z_{0t23} = 178.5275\:\Omega,\: C_{t2} = 3.77241\text{ pF}\). Dibuje la disposición física del circuito asumiendo que se utilizarán capacitores de elementos grumados. Calcular los anchos y longitudes de las líneas de microcinta si el grosor del sustrato de microcinta es\(500\:\mu\text{m}\) y la permitividad relativa del sustrato es\(10\). El uso puede usar, con algún error, las Figuras 5-10—5-13 y/o las Tablas 5-2—5-3 de [29] en el cálculo de los anchos y separaciones de las líneas acopladas incluso si la impedancia de su sistema no lo es\(50\:\Omega\).

3.8.1 Ejercicios por Sección

\(†\)desafiante,\(‡\) muy desafiante

\(§3.2\: 1†, 2†, 3†, 4†, 5†, 6†\)

\(§3.4\: 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18†, 19†, 20, 21†, 22, 23, 24†, 25†, 26†, 27†, 28†, 29‡, 30‡, 31‡\)

3.8.2 Respuestas a Ejercicios Seleccionados

1. (d)\(2\:\Omega\)

3. \(5.5\)

5. (d)\(5\)
6. c)\(0\:\Omega\)

14. \(\lambda /8\)

16. b)\(\jmath [C+1/(\omega_{0}^{2}L)]\)

18. \(9.5\text{ pF}\)

20. (a)\(\infty\)

30. (d)\(1.48\text{ cm}\)
31. \(39.4\:\Omega\)

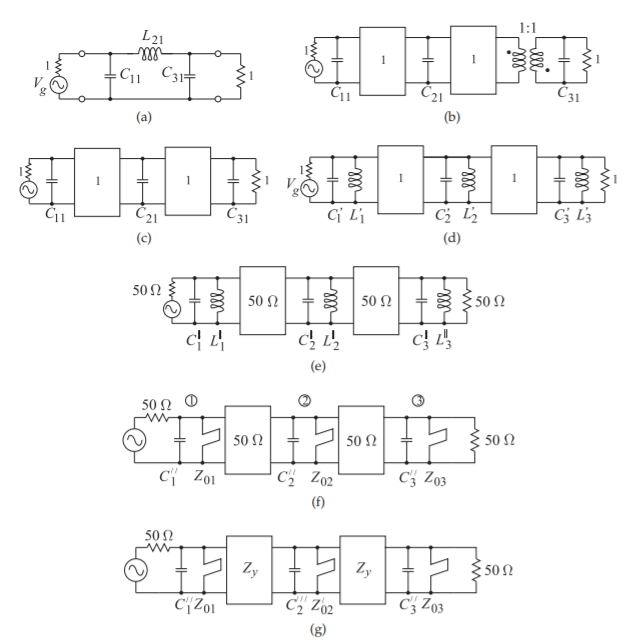
Figura\(\PageIndex{1}\): Prototipos tempranos en el desarrollo de un filtro combinado Butterworth de tercer orden.

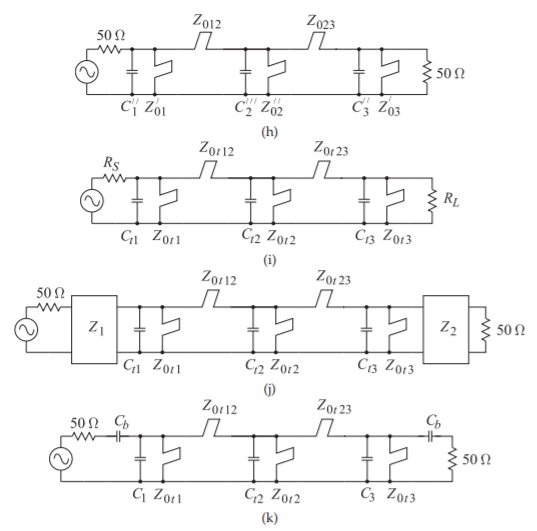
Figura\(\PageIndex{2}\): Prototipos en etapa tardía en el desarrollo de un filtro combinado Butterworth de tercer orden.