4.5: Ruido del oscilador

El ruido en los osciladores tiene una característica particular que afecta el uso de osciladores en sistemas de RF. Al oscilar, la frecuencia de oscilación varía ligeramente y esta variación se captura como ruido de fase.

4.4.1 Observaciones de espectros de ruido de osciladores

En el dominio de la frecuencia, el ruido se caracteriza por su densidad espectral de potencia\(S\), que es la potencia de ruido en un ancho de banda especificado. Es típico usar\(1\text{ Hz}\) como ancho de banda de referencia y luego\(S\) se expresa en unidades de vatios por hercio o, más comúnmente,\(\text{dBm}\) según hercios. Algunos tipos de ruido son proporcionales a la señal de RF o nivel de portadora y se expresan en relación con el nivel de la portadora como\(\text{dBc/Hz}\) (\(10 \log\)de la relación de la potencia de ruido por hercios en relación con la potencia de la portadora). El ruido se puede descomponer en un componente de fase\(S_{\varphi}\), y un componente de amplitud,\(S_{a}\). Entonces las fluctuaciones de fase observadas, clasificadas en [18], son como se muestra en la Figura\(\PageIndex{1}\). También hay fluctuaciones de amplitud que tienen una característica similar. Por ejemplo, el ruido de amplitud parpadeante también tendrá una\(f^{−1}\) dependencia. Sin embargo, el componente de fase generado por los circuitos electrónicos recibe la mayor atención ya que las pequeñas variaciones de amplitud son apagadas por las no linealidades del dispositivo. En la Figura\(\PageIndex{1}\), el registro de

Frecuencia\((\text{GHZ})\)	\(F_{\text{min}}\)	\(\text{NF}_{\text{min}}\)\((\text{dB})\)	\(\Gamma_{n}\)	\(\angle\Gamma_{n}\)grados	\(r_{n}/50\)\((\Omega )\)
\ ((\ text {GHZ})\) ">\(0.90\)	\ (F_ {\ texto {min}}\) ">\(1.07\)	\ (\ texto {NF} _ {\ texto {min}}\)\((\text{dB})\) “>\(0.29\)	\ (\ Gamma_ {n}\) ">\(0.747\)	\ (\ ángulo\ Gamma_ {n}\) grados">\(15.70\)	\ (r_ {n} /50\)\((\Omega )\) “>\(0.165\)
\ ((\ text {GHZ})\) ">\(1.80\)	\ (F_ {\ texto {min}}\) ">\(1.09\)	\ (\ texto {NF} _ {\ texto {min}}\)\((\text{dB})\) “>\(0.38\)	\ (\ Gamma_ {n}\) ">\(0.623\)	\ (\ ángulo\ Gamma_ {n}\) grados">\(24.95\)	\ (r_ {n} /50\)\((\Omega )\) “>\(0.176\)
\ ((\ text {GHZ})\) ">\(2.40\)	\ (F_ {\ texto {min}}\) ">\(1.11\)	\ (\ texto {NF} _ {\ texto {min}}\)\((\text{dB})\) “>\(0.44\)	\ (\ Gamma_ {n}\) ">\(0.795\)	\ (\ ángulo\ Gamma_ {n}\) grados">\(37.45\)	\ (r_ {n} /50\)\((\Omega )\) “>\(0.158\)
\ ((\ text {GHZ})\) ">\(2.60\)	\ (F_ {\ texto {min}}\) ">\(1.11\)	\ (\ texto {NF} _ {\ texto {min}}\)\((\text{dB})\) “>\(0.47\)	\ (\ Gamma_ {n}\) ">\(0.640\)	\ (\ ángulo\ Gamma_ {n}\) grados">\(47.15\)	\ (r_ {n} /50\)\((\Omega )\) “>\(0.159\)
\ ((\ text {GHZ})\) ">\(2.80\)	\ (F_ {\ texto {min}}\) ">\(1.12\)	\ (\ texto {NF} _ {\ texto {min}}\)\((\text{dB})\) “>\(0.49\)	\ (\ Gamma_ {n}\) ">\(0.670\)	\ (\ ángulo\ Gamma_ {n}\) grados">\(47.90\)	\ (r_ {n} /50\)\((\Omega )\) “>\(0.160\)
\ ((\ text {GHZ})\) ">\(3.20\)	\ (F_ {\ texto {min}}\) ">\(1.13\)	\ (\ texto {NF} _ {\ texto {min}}\)\((\text{dB})\) “>\(0.53\)	\ (\ Gamma_ {n}\) ">\(0.617\)	\ (\ ángulo\ Gamma_ {n}\) grados">\(51.20\)	\ (r_ {n} /50\)\((\Omega )\) “>\(0.156\)
\ ((\ text {GHZ})\) ">\(4.00\)	\ (F_ {\ texto {min}}\) ">\(1.15\)	\ (\ texto {NF} _ {\ texto {min}}\)\((\text{dB})\) “>\(0.61\)	\ (\ Gamma_ {n}\) ">\(0.542\)	\ (\ ángulo\ Gamma_ {n}\) grados">\(68.70\)	\ (r_ {n} /50\)\((\Omega )\) “>\(0.141\)
\ ((\ text {GHZ})\) ">\(5.00\)	\ (F_ {\ texto {min}}\) ">\(1.18\)	\ (\ texto {NF} _ {\ texto {min}}\)\((\text{dB})\) “>\(0.72\)	\ (\ Gamma_ {n}\) ">\(0.465\)	\ (\ ángulo\ Gamma_ {n}\) grados">\(85.00\)	\ (r_ {n} /50\)\((\Omega )\) “>\(0.120\)
\ ((\ text {GHZ})\) ">\(5.50\)	\ (F_ {\ texto {min}}\) ">\(1.19\)	\ (\ texto {NF} _ {\ texto {min}}\)\((\text{dB})\) “>\(0.77\)	\ (\ Gamma_ {n}\) ">\(0.431\)	\ (\ ángulo\ Gamma_ {n}\) grados">\(91.10\)	\ (r_ {n} /50\)\((\Omega )\) “>\(0.114\)
\ ((\ text {GHZ})\) ">\(6.00\)	\ (F_ {\ texto {min}}\) ">\(1.21\)	\ (\ texto {NF} _ {\ texto {min}}\)\((\text{dB})\) “>\(0.83\)	\ (\ Gamma_ {n}\) ">\(0.366\)	\ (\ ángulo\ Gamma_ {n}\) grados">\(101.15\)	\ (r_ {n} /50\)\((\Omega )\) “>\(0.107\)
\ ((\ text {GHZ})\) ">\(7.00\)	\ (F_ {\ texto {min}}\) ">\(1.24\)	\ (\ texto {NF} _ {\ texto {min}}\)\((\text{dB})\) “>\(0.93\)	\ (\ Gamma_ {n}\) ">\(0.262\)	\ (\ ángulo\ Gamma_ {n}\) grados">\(122.10\)	\ (r_ {n} /50\)\((\Omega )\) “>\(0.096\)
\ ((\ text {GHZ})\) ">\(8.00\)	\ (F_ {\ texto {min}}\) ">\(1.27\)	\ (\ texto {NF} _ {\ texto {min}}\)\((\text{dB})\) “>\(1.04\)	\ (\ Gamma_ {n}\) ">\(0.188\)	\ (\ ángulo\ Gamma_ {n}\) grados">\(153.60\)	\ (r_ {n} /50\)\((\Omega )\) “>\(0.100\)
\ ((\ text {GHZ})\) ">\(9.00\)	\ (F_ {\ texto {min}}\) ">\(1.30\)	\ (\ texto {NF} _ {\ texto {min}}\)\((\text{dB})\) “>\(1.14\)	\ (\ Gamma_ {n}\) ">\(0.135\)	\ (\ ángulo\ Gamma_ {n}\) grados">\(-165.60\)	\ (r_ {n} /50\)\((\Omega )\) “>\(0.121\)
\ ((\ text {GHZ})\) ">\(10.00\)	\ (F_ {\ texto {min}}\) ">\(1.33\)	\ (\ texto {NF} _ {\ texto {min}}\)\((\text{dB})\) “>\(1.25\)	\ (\ Gamma_ {n}\) ">\(0.162\)	\ (\ ángulo\ Gamma_ {n}\) grados">\(-126.80\)	\ (r_ {n} /50\)\((\Omega )\) “>\(0.138\)
\ ((\ text {GHZ})\) ">\(11.00\)	\ (F_ {\ texto {min}}\) ">\(1.37\)	\ (\ texto {NF} _ {\ texto {min}}\)\((\text{dB})\) “>\(1.35\)	\ (\ Gamma_ {n}\) ">\(0.183\)	\ (\ ángulo\ Gamma_ {n}\) grados">\(-85.95\)	\ (r_ {n} /50\)\((\Omega )\) “>\(0.187\)
\ ((\ text {GHZ})\) ">\(12.00\)	\ (F_ {\ texto {min}}\) ">\(1.40\)	\ (\ text {NF} _ {\ text {min}}\)\((\text{dB})\) “>\(1.46\)	\ (\ Gamma_ {n}\) ">\(0.270\)	\ (\ ángulo\ Gamma_ {n}\) grados">\(-68.40\)	\ (r_ {n} /50\)\((\Omega )\) “>\(0.239\)
\ ((\ text {GHZ})\) ">\(13.00\)	\ (F_ {\ texto {min}}\) ">\(1.43\)	\ (\ text {NF} _ {\ text {min}}\)\((\text{dB})\) “>\(1.57\)	\ (\ Gamma_ {n}\) ">\(0.343\)	\ (\ ángulo\ Gamma_ {n}\) grados">\(-50.25\)	\ (r_ {n} /50\)\((\Omega )\) “>\(0.355\)
\ ((\ text {GHZ})\) ">\(14.00\)	\ (F_ {\ texto {min}}\) ">\(1.47\)	\ (\ text {NF} _ {\ text {min}}\)\((\text{dB})\) “>\(1.67\)	\ (\ Gamma_ {n}\) ">\(0.431\)	\ (\ ángulo\ Gamma_ {n}\) grados">\(-43.95\)	\ (r_ {n} /50\)\((\Omega )\) “>\(0.461\)
\ ((\ text {GHZ})\) ">\(15.00\)	\ (F_ {\ texto {min}}\) ">\(1.51\)	\ (\ text {NF} _ {\ text {min}}\)\((\text{dB})\) “>\(1.78\)	\ (\ Gamma_ {n}\) ">\(0.573\)	\ (\ ángulo\ Gamma_ {n}\) grados">\(-25.80\)	\ (r_ {n} /50\)\((\Omega )\) “>\(0.604\)

Tabla\(\PageIndex{1}\): Parámetros de ruido de un transistor PhEMT en modo de mejora modelo FPD6836P70 [17]. \(F_{\text{min}}\)es el factor de ruido mínimo,\(\text{NF}_{\text{min}}\) es la cifra de ruido mínimo y\(\Gamma_{n} = \Gamma_{\text{opt}}\) es el coeficiente de reflexión de origen que produce\(F_{\text{min}}\).

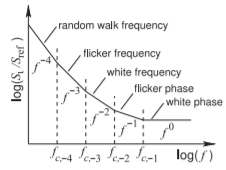
Figura\(\PageIndex{1}\): Ruido de banda ancha que muestra solo ruido de fase y frecuencia. \(S_{\varphi}\)es la densidad espectral del ruido de fase y\(f\) es la frecuencia.

la densidad espectral de potencia de ruido de fase relativa a un nivel de referencia se representa como una función del log de frecuencia. El gráfico no baja hasta DC porque el eje de frecuencia es logarítmico. Esto no implica que la potencia del ruido vaya al infinito\(^{1}\) ya que, por supuesto, el ancho de banda es cada vez más pequeño a baja\(\log(f)\).

La figura\(\PageIndex{1}\) es la forma habitual de trazar el ruido, ya que las regiones de línea recta se observan claramente de manera experimental y en estas regiones la densidad espectral de potencia de ruido varía con la frecuencia como\(1/f^{n}\), donde\(n\) es un entero positivo. A veces faltarán una o más de estas regiones, y esto se interpreta como las frecuencias de cruce\(\PageIndex{1}\), estando fuera de orden las\(f_{c−n}\) s de la Figura.

La característica de ruido observada (Figura\(\PageIndex{1}\)) es intrigante. ¿Por qué hay regiones de línea recta y cuáles son los procesos físicos que producen ruido con tales características? Las regiones de línea recta están en contraste con lo que, quizás, podría esperarse que sea una transición continua suave de una región de baja densidad espectral a una región de alta densidad espectral.

Se han dado nombres a las regiones [18], siendo la primera ruido de fase blanca, ruido sin dependencia de frecuencia (es decir, una dependencia de frecuencia de\(f^{0}\)). Este ruido tiene una media y una varianza pero no mayor (es decir, tercer y superior) momento. En el dominio del tiempo este ruido tiene (en realidad se supone que tiene) una distribución gaussiana. Esta es la forma de ruido que se puede traducir entre los dominios de tiempo y frecuencia usando cálculo entero.

La siguiente región de ruido que se ve en la Figura\(\PageIndex{1}\) se denomina región de ruido de fase de parpadeo con densidad espectral de ruido dependiente de\(1/f\) (o\(f^{−1}\)). Tradicionalmente esta ha sido una característica de ruido desconcertante y posiblemente se deba a un comportamiento caótico. La\(1/f\) característica indica que hay memoria a largo plazo, lo que es lo mismo que decir que las fluctuaciones (es decir, el ruido) están correlacionadas con las fluctuaciones en tiempos pasados. En los sistemas de RF y microondas, el ruido de fase de parpadeo suele ser el ruido más significativo y establece los límites de rendimiento relacionados con el ruido en los circuitos receptores en particular. El consumo de energía también se ve afectado ya que el ruido de parpadeo generalmente se suprime por el aumento de las corrientes de polarización Siguiendo la\(1/f\) región están la frecuencia blanca\(f^{−2}\), frecuencia de parpadeo,\(f^{−3}\), y regiones de frecuencia de caminata aleatoria,\(f^{−4}\). Estas regiones también indican correlación de fluctuaciones a largo plazo. Se ha demostrado que al menos parte del ruido en la\(f^{−2}\) región es dado a ruido blanco convertido ascendentemente de cerca de CC [22] y de ruido blanco cerca de armónicos de la señal oscilante [23].

En RF el ruido de mayor interés es el ruido superpuesto a una señal que se amplifica, o el ruido que es generado por un oscilador. Este ruido tiene un componente de ruido blanco y uno o más componentes con\(1/(\Delta f)^{n}\) dependencia, donde\(n\) es un entero positivo y\(\Delta f\) es el desplazamiento de la frecuencia de la señal central. Se ha encontrado que el ruido con\(1/(\Delta f)^{n}\) dependencia

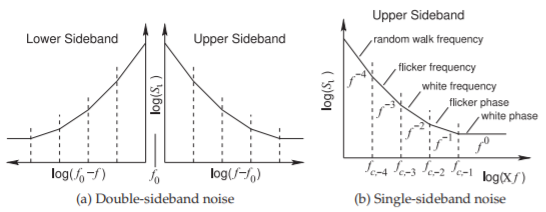
Figura\(\PageIndex{2}\): Ruido de banda estrecha alrededor de la frecuencia portadora,\(f_{0}\), de un oscilador que muestra solo ruido de fase y frecuencia con\(\Delta f = f − f_{0}\).

estar al menos parcialmente relacionado con el ruido observado a bajas frecuencias. (Este es otro indicio de nuestra falta de una comprensión completa del ruido.)

El ruido de fase observado en la señal producida por un oscilador se muestra en la Figura\(\PageIndex{2}\) (a). Si bien el ruido aparece tanto por encima como por debajo de la frecuencia oscilante, el llamado ruido de doble banda lateral, generalmente solo se traza la banda lateral superior, como se muestra en la Figura\(\PageIndex{2}\) (b). Las designaciones de las regiones de línea recta [18] (ver Figura\(\PageIndex{2}\) (b)) corresponden a las designaciones para ruido de baja frecuencia (ver Figura\(\PageIndex{1}\)). El ruido observado en una señal de oscilación o en la señal en la salida de un amplificador debe, necesariamente, provenir del procesamiento de una fuente de ruido físico.

El ruido en la señal en la salida de un oscilador es casi en su totalidad fluctuaciones de fase, ya que la saturación apaga las fluctuaciones de amplitud. Las fluctuaciones de fase en el dominio de frecuencia se caracterizan por la densidad espectral de las fluctuaciones de fase. Si la señal en la salida del oscilador es

\[\label{eq:1}v(t)=[V_{0}+\epsilon (t)]\sin[2\pi f_{0}t+\phi(t)] \]

donde\(\epsilon (t)\) está la fluctuación de amplitud y\(\phi (t)\) es la fluctuación de fase, la densidad espectral de las fluctuaciones de fase es

\[\label{eq:2}S_{\phi}(\Delta f)=S_{\phi}(\Delta\omega)=\text{PSD}[\phi (t)]=\frac{E[\phi^{2}(t)]}{B} \]

donde\(\Delta f = \Delta\omega /(2\pi )\) está el desplazamiento de frecuencia de la portadora en frecuencia\(f_{0}\),\(\text{PSD}\) se refiere a la densidad espectral de potencia,\(E[\:]\) se refiere al valor estimado (aquí la media de la fase al cuadrado), y\(B\) es el ancho de banda sobre el que se realiza la estimación (es decir, el ancho de banda del medición). Con ancho de banda teniendo las unidades de hertz, entonces las unidades de\(S_{\phi}\) son radianes\(^{2}/\text{Hz}\). \(\eqref{eq:2}\)La ecuación incluye contribuciones tanto de las bandas laterales superior como inferior y, por lo tanto, es una medida de doble banda lateral del ruido de fase. La medida preferida es la densidad espectral de ruido de fase de banda lateral única\(\mathcal{L}\) (leída como Script-L) de modo que\(^{2}\)

\[\label{eq:3}\mathcal{L}(f)=\frac{1}{2}S_{\phi}(f) \]

Notas al pie

[1] Más importante aún, la integración, usando cálculo entero, no es válida. Se cree que el ruido que tiene el espectro\(1/f\) similar es fractal (es decir, de origen caótico). Los fractales son formalmente irregulares, rugosos e indiferenciables. Es decir, los procesos fractales son inaccesibles al tratamiento por cálculo entero y por lo tanto no tienen un espectro de potencia [19]. Sin embargo, se ha demostrado que tal proceso cuando pasa a través de un filtro de paso de banda ideal se volverá estacionario y luego tendrá un espectro de potencia [20, 21]. Lo que esto significa es que dado que los equipos de medición son de banda limitada, el espectro medido puede parecer acercarse al infinito a medida que el desplazamiento va a cero, pero el proceso de ruido físico subyacente no lo hará. Además, el filtro de paso de banda real de los equipos de medición tiene pérdidas y por lo tanto un artefacto de medición es que las mediciones de ruido se nivelarán para desplazamientos de frecuencia cada vez más pequeños.

[2] En el pasado,\(\mathcal{L}(f)\) se definía como la potencia de ruido de banda lateral única en un\(1\text{ Hz}\) ancho de banda dividido por la potencia de la portadora. Esta definición ha sido reemplazada por Ecuación\(\eqref{eq:3}\) debido a ambigüedades en la aplicación de la antigua definición cuando las fluctuaciones tanto de amplitud como de fase son significativas.