4.7: Rango dinámico

Si bien los sistemas modernos de comunicación y radar utilizan señales moduladas digitalmente, las señales de dos tonos se utilizan para caracterizar la no linealidad (generalmente) y también en cálculos manuales. A potencias bajas antes de que la compresión se convierta en factor, la respuesta fundamental (es decir, la potencia de salida frente a la potencia de entrada) inicialmente tiene una\(1:1\) pendiente con respecto a la entrada, como se muestra en la Figura\(\PageIndex{2}\). La respuesta de intermodulación de tercer orden, IM3, varía según el cubo del nivel de tonos de entrada cuando ambos tonos varían en la misma cantidad, como es común en una prueba de dos tonos. Así, la respuesta IM3 inicialmente tiene una pendiente\(3:1\) logarítmica con respecto a la entrada. Dado que las relaciones son lineales en un sentido log-log, es posible describir el rendimiento no lineal de un amplificador por una cantidad llamada rango dinámico (DR) o por el rango dinámico libre espurio similar (SFDR). SFDR describe la diferencia entre el nivel en el que se distorsiona una señal y el nivel de ruido (es decir, el piso de ruido). DR es similar a SFDR excepto que el nivel del mínimo discernible

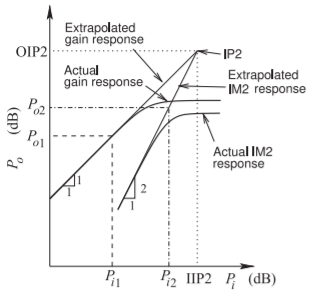
Figura\(\PageIndex{1}\): Potencia de salida versus potencia de entrada de un amplificador trazado en una escala logarítmica. La respuesta IM2 es resultado de la intermodulación de dos tonos (o de generación armónica), y la potencia de entrada es la potencia de cada una de las dos señales que tienen igual amplitud. Extrapolaciones de la respuesta fundamental\(1:1\) lineal y la respuesta de\(2:1\) segundo orden se cruzan en el punto IP2.

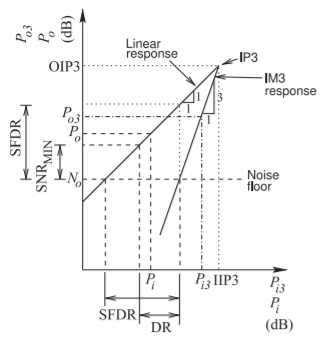
Figura\(\PageIndex{2}\): Potencia de salida versus potencia de entrada de una etapa o sistema trazada como potencia de salida en decibelios versus potencia de entrada en decibelios. La respuesta IM3 es resultado de la intermodulación de dos tonos, y la potencia de entrada es la potencia combinada de las dos señales que tienen igual amplitud. Extrapolaciones de la respuesta fundamental\(1:1\) lineal y la respuesta de intermodulación de\(3:1\) tercer orden se cruzan en el punto IP3.

señal (MDS) (también llamada la señal mínima detectable) se utiliza en lugar del piso de ruido. El MDS es mayor que el nivel del piso de ruido por el SNR mínimo aceptable (SNR\(_{\text{MIN}}\)). SNR\(_{\text{MIN}}\) depende del tipo de modulación, de las insuficiencias de hardware (capturadas por el margen de implementación), de la ganancia de procesamiento y de la codificación de corrección de errores utilizada en un protocolo de comunicaciones particular.

Es interesante señalar que el nivel de compresión de\(1\text{ dB}\) ganancia no tiene ningún efecto sobre el rango dinámico de los circuitos y sistemas de microondas. Esto se debe a que el rango dinámico se refiere a la capacidad de detectar una señal cuando es posible que la señal deseada sea enmascarada por señales espurias. La compresión de ganancia por sí sola no introduce señales espurias por lo que no interfiere con la capacidad de detectar una señal pequeña.

El rango dinámico no se relaciona con la precisión con la que la señal recibida muestreada coincide con el diagrama de constelación de la señal modulada digitalmente transmitida. La distorsión del diagrama de constelación está determinada por el ruido, la compresión de ganancia y la distorsión de intermodulación.

A continuación, se desarrolla una expresión para SFDR en términos de cantidades referenciadas de entrada, y esta forma del SFDR se denomina SFDR de entrada (SFDR\(_{i}\)). También se desarrolla un rango dinámico (DR\(_{i}\)) de referencia similar.

La figura define\(\PageIndex{2}\) gráficamente los rangos dinámicos. El punto de intersección de las respuestas lineales extrapoladas e IM3 se denomina punto de intercepción de tercer orden (intercepción IP3). El punto se identifica por la potencia de intercepción referida a la salida (OIP3) o por la potencia de intercepción IP3 referida a entrada (IIP3) y estos son parámetros clave para describir la linealidad de los subsistemas no lineales.

En la región de ganancia lineal, la potencia de salida\(P_{o}\) versus la potencia de entrada\(P_{i}\) tiene una pendiente de\(1:1\), de modo que

\[\label{eq:1}P_{\text{dBm},i}=P_{\text{dBm},o}-G_{\text{dB}} \]

donde\(G_{\text{dB}}\) esta la ganancia de poder en decibelios. \(P_{o}\)se utiliza aquí como la potencia de salida, con\(P_{\text{dBm},o}\) indicación de la potencia de salida en\(\text{dBm}\). \(P_{i}\)y\(P_{\text{dBm},i}\) se definen de manera similar. En términos de cantidades de entrada

\[\label{eq:2}\text{IIP3}=\frac{\text{OIP3}}{G}=\text{IIP3}_{\text{dBm}}=\text{OIP3}_{\text{dBm}}-G_{\text{dB}} \]

donde nuevamente el\(\text{dBm}\) subíndice indica que la cantidad se expresa en decibelios referidos\(1\text{ mW}\).

La no linealidad de los componentes activos de RF da como resultado armónicos y componentes de intermodulación. Con los amplificadores de banda estrecha de los sistemas de comunicación y radar, los filtros de salida filtran convenientemente los armónicos. Sin embargo, la distorsión de intermodulación no se puede filtrar, ya que estos componentes están dentro de la banda de paso principal. Los componentes de intermodulación son, por lo tanto, tonos espurios. Generalmente solo uno de estos define el tono espurio máximo y casi siempre es uno de los tonos de intermodulación de tercer orden resultantes de una entrada de dos tonos. La consideración del tono espurio máximo y el piso de ruido define el SFDR.

Examinando la Figura\(\PageIndex{2}\) conduce a la siguiente desigualdad describiendo la ganancia lineal del amplificador:

\[\begin{align}\frac{\text{OIP3}_{\text{dBm}}-P_{\text{dBm},o}}{\text{IIP3}_{\text{dBm}}-P_{\text{dBm},i}}&=\frac{\text{OIP3}_{\text{dBm}}-P_{\text{dBm},o}}{(\text{OIP3}_{\text{dBm}}-G_{\text{dB}})-P_{\text{dBm},i}}\nonumber \\ \label{eq:3}&=1\end{align} \]

La respuesta IM3 se caracteriza por introducir primero una potencia de entrada equivalente,\(P_{\text{dBm},i3}\) (\(P_{i3}\)expresada en\(\text{dBm}\)), definida como la potencia promedio de la señal de dos tonos que genera un IM3 de potencia\(P_{\text{dBm},o3}\). Observando que\(P_{\text{dBm},o3}\) varía con una pendiente\(3:1\) logarítmica con respecto a\(P_{\text{dBm},i3}\), entonces

\[\label{eq:4}\frac{\text{OIP3}_{\text{dBm}}-P_{\text{dBm},o3}}{(\text{OIP3}_{\text{dBm}}-G_{\text{dB}})-P_{\text{dBm},i3}}=3 \]

o

\[\label{eq:5}P_{\text{dBm},i3}=\frac{1}{3}(2\cdot\text{OIP3}_{\text{dBm}}+P_{\text{dBm},o3}-3G_{\text{dB}}) \]

El SFDR ahora se puede definir cuando el producto de intermodulación de tercer orden de la excitación de dos tonos es el tono espurio dominante. El SFDR se define como la diferencia entre\(P_{i3}\) y\(P_{i}\) cuando producen IM3 y salida lineal, respectivamente, que son ambas iguales a la potencia de ruido de salida,\(N_{o}\) (ver Figura\(\PageIndex{2}\)); es decir, cuándo\(P_{o} = P_{o3} = N_{o}\). Sustitución\(P_{\text{dBm},o}\) en Ecuación\(\eqref{eq:5}\) con\(N_{o}\) da

\[\label{eq:6}P_{\text{dBm},i3}=\frac{1}{3}(2\cdot\text{OIP3}_{\text{dBm}}+N_{\text{dBm},o}-3G_{\text{dB}}) \]

y

\[\label{eq:7}P_{\text{dBm},i}=N_{\text{dBm},o}-G_{\text{dB}} \]

Tenga en cuenta que la diferencia entre la salida lineal y la intermodulación de tercer orden se reduce a medida que la potencia de entrada aumenta por encima\(P_{i3}\). Por lo tanto, el SFDR referido a la salida es

\[\begin{align}\text{SFDR}_{\text{dB},o}&=P_{\text{dBm},i3}-P_{\text{dBm},i}\nonumber \\ &=\frac{2}{3}\text{OIP3}_{\text{dBm}}+\frac{1}{3}N_{\text{dBm},o}-G_{\text{dB}}-N_{\text{dBm},o}+G_{\text{dB}}\nonumber \\ \label{eq:8}&=\frac{2}{3}(\text{OIP3}_{\text{dBm}}-N_{\text{dBm},o})\end{align} \]

Entonces SFDR es\(2/3\) rds del rango en decibelios desde la intercepción de ruido hasta el punto de intercepción de tercer orden. Un desarrollo similar define el SFDR idéntico de entrada referida:

\[\label{eq:9}\text{SFDR}_{\text{dB},i}=\frac{2}{3}(\text{IIP3}_{\text{dBm}}-N_{\text{dBM},i}) \]

Tenga en cuenta que\(N_{i}\) es el ruido de entrada referido e incluye el ruido aplicado al módulo así como el ruido producido internamente en el módulo y referido a la entrada. El SFDR proporciona una medida combinada de distorsión y ruido. Sin embargo, para el rango dinámico utilizable se debe considerar la SNR mínima aceptable. El SNR mínimo (SNR\(_{\text{MIN}}\)) requerido está determinado por el formato de comunicación o modulación de radar, codificación de errores y BER aceptable. Entonces, al definir DR, la potencia de entrada de la señal deseada debe aumentar lo suficiente para producir una SNR de al menos SNR\(_{\text{MIN}}\). Dado que el nivel espurio deseado se encuentra todavía en el piso de ruido, esto implica una resta directa en decibelios de la SNR deseada. Por lo tanto, el rango dinámico de tercer orden referido a entrada, preferido para receptores, es

\[\label{eq:10}\text{DR}_{i}=\frac{2}{3}(\text{IIP3}_{\text{dBm}}-N_{\text{dBm},i}-\text{SNR}_{\text{dB, MIN}}) \]

y el rango dinámico referido a la salida, preferido para los transmisores, es

\[\label{eq:11}\text{DR}_{o}=\frac{2}{3}(\text{OIP3}_{\text{dBm}}-N_{\text{dBm},o}-\text{SNR}_{\text{MIN}}) \]

La señal mínima discernible en la salida es

\[\label{eq:12}\text{MDS}_{\text{dBm},o}=N_{\text{dBm},o}+\text{SNR}_{\text{dB},\text{MIN}} \]

por lo que el rango dinámico referido a la salida se puede escribir como

\[\label{eq:13}\text{DR}_{o}=\frac{2}{3}(\text{OIP3}_{\text{dBm}}-\text{MDS}_{\text{dBm},o}) \]

Entonces DR es\(2/3\) rds del rango en decibelios desde el nivel de la señal mínima detectable hasta el punto de intercepción de tercer orden. La señal mínima discernible en la entrada es

\[\label{eq:14}\text{MDS}_{\text{dBm},i}=N_{\text{dBm},i}+\text{SNR}_{\text{dB, MIN}} \]

y el rango dinámico de entrada (igual a\(\text{DR}_{o}\)) puede escribirse como

\[\label{eq:15}\text{DR}_{i}=\frac{2}{3}(\text{IIP3}_{\text{dBm}}-\text{MDS}_{\text{dBm},i}) \]