5.5: Componentes de ferrita - Circuladores y Aisladores

Los circuladores y aisladores son dispositivos no recíprocos que enrutan preferentemente las señales de RF [14, 15, 16]. El elemento esencial de un circulador es una losa o disco de ferrita que, al magnetizarse, se vuelve no recíproco, con una dirección preferida de propagación resultante de lo que se denomina efecto giromagnético.

5.5.1 Efecto giromagnético

Un electrón tiene un campo magnético intrínseco descrito por su momento magnético\(m\) (ver Figura\(\PageIndex{1}\) (a)) [17]. Esto se debe a una propiedad mecánica cuántica llamada spin bu el electrón en realidad no gira. En la mayoría de los materiales el espín electrónico ocurre en pares con el campo magnético producido por el espín de un electrón siendo cancelado por el espín del otro electrón. Sin embargo, en algunos materiales el giro no ocurre en pares y hay regiones en las que los pequeños campos magnéticos producidos a nivel atómico se alinean para producir regiones organizadas de campo magnético dirigido. Estas regiones se llaman dominios, o a veces dominios magnéticos, y el campo magnético combinado de los espines electrónicos alineados se llama momento magnético.

El material magnético más común es la ferrita, que es una cerámica que contiene óxido de hierro (III) (\(\text{Fe}_{2}\text{O}_{3}\)). Se obtienen efectos magnéticos muy fuertes con materiales que contienen elementos de tierras raras. Los elementos de tierras raras, los elementos lantanoides, pueden alinear los espines de muchos electrones de cada átomo y pueden producir dominios magnéticos y momentos magnéticos particularmente fuertes. Los elementos de tierras raras más comunes utilizados en materiales magnéticos son el samario y el neodimio utilizados en imanes de samario-cobalto y neodimiumirón-boro, respectivamente.

Los dominios pueden ser alineados por un fuerte magnético generado externamente

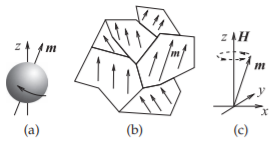
Figura\(\PageIndex{1}\): Momentos magnéticos: (a) electrón con el momento magnético\(m\); (b), dominios magnéticos; y (c) progresión con polarización de campo magnético.

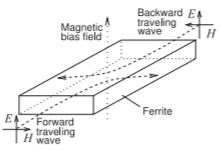
Figura\(\PageIndex{2}\): Efecto giromagnético sobre la propagación de ondas EM en un material magnético (aquí una ferrita) con un campo de polarización magnético aplicado externamente.

(por ejemplo, usando un electroimán), y una vez que los dominios están alineados, pueden permanecer así durante años incluso cuando se elimina el campo externo. Esta situación se muestra en la Figura\(\PageIndex{1}\) (b), donde los dominios individuales han sido casi completamente alineados. Cada cristal del material generalmente tendrá muchos dominios magnéticos y un dominio puede crecer en tamaño (mientras que otro se reduce o desaparece), pero generalmente un dominio no cruzará un límite cristalino. Los dominios también pueden ser rotados parcialmente por un campo magnético aplicado moderado y cuando se elimina el campo aplicado, los dominios vuelven a su alineación original. El resultado es que la energía magnética se almacena de la misma manera que la energía se almacena en un resorte. La cantidad de energía que se almacena depende de la orientación del campo magnético aplicado a los dominios. La capacidad de almacenamiento de energía se describe por la permeabilidad del material. En ausencia de un campo magnético de polarización constante, la permeabilidad tendría tres valores, uno para cada una de las\(z\) direcciones\(x\)\(y\),, y.

Una propiedad de microondas muy interesante ocurre cuando el material magnético es polarizado por un fuerte campo magnético de CC. Esta situación se representa en la Figura\(\PageIndex{1}\) (c). Cuando también se aplica un campo magnético variable en el tiempo (por ejemplo, el componente magnético de un campo EM), el vector de momento magnético tenderá a girar alrededor del campo magnético de CC como se muestra. Esto se llama el efecto giromagnético. Cuando la frecuencia del campo aplicado corresponde a la frecuencia característica de rotación del momento magnético entonces el efecto se denomina resonancia giromagnética y hay rotación sostenida de baja pérdida.

Incluso sin resonancia (porque el campo de polarización magnética es demasiado pequeño) el efecto giromagnético afecta la forma en que se propaga un campo de RF y esto es descrito por una permeabilidad de nueve elementos llamada tensor (o un tensor diádico o diádico) que relaciona cada uno de los tres\(H\) campos componentes (en las\(z-\) direcciones\(x-\),\(y-\), y) a cada uno de los tres componentes de\(B\) campo. La permeabilidad de un material magnético polarizado magnéticamente es:

\[\label{eq:1}\left[\mu\right] =\left[\begin{array}{ccc}{\mu_{xx}}&{\mu_{xy}}&{\mu_{xz}} \\ {\mu_{yx}}&{\mu_{yy}}&{\mu_{yz}} \\ {\mu_{zx}}&{\mu_{zy}}&{\mu_{zz}}\end{array}\right] =\left[\begin{array}{ccc}{\mu_{0}}&{0}&{0} \\ {0}&{\mu}&{\jmath\kappa} \\ {0}&{-\jmath\kappa}&{\mu}\end{array}\right] \]

Este tensor puede tomar otras formas dependiendo de la orientación del campo magnético variable en el tiempo con respecto al campo magnético de polarización de CC.

El efecto sobre la propagación de un campo EM se muestra en la Figura\(\PageIndex{2}\). Cuando el campo EM está en el material magnético magnetizado, la onda no viaja en línea recta y en su lugar se curva, en este caso, hacia la derecha. Así, las ondas que viajan hacia adelante y hacia atrás divergen entre sí y la propagación no es recíproca. Esto se puede utilizar para separar las olas que viajan hacia adelante y hacia atrás. A esto se le llama desplazamiento de campo.

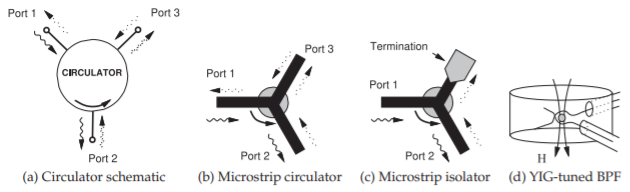
Figura\(\PageIndex{3}\): Componentes de ferrita [21].

5.2.2 Circulador

Un circulador explota el efecto giromagnético a través del desplazamiento de campo [18, 19, 20]. El esquema de un circulador se muestra en la Figura\(\PageIndex{3}\) (a), donde las flechas indican que la señal que ingresa a Puerto\(\mathsf{1}\) del circulador sale del circulador en Puerto\(\mathsf{2}\) y no en Puerto\(\mathsf{3}\). De manera similar, la energía que ingresa en Puerto\(\mathsf{2}\) se encamina a Puerto\(\mathsf{3}\), y la energía que ingresa en Puerto\(\mathsf{3}\) se encamina a Puerto\(\mathsf{1}\). En términos de\(S\) parámetros, un circulador ideal tiene la matriz de dispersión

\[\label{eq:2}\mathbf{S}=\left[\begin{array}{ccc}{0}&{0}&{S_{13}}\\{S_{21}}&{0}&{0}\\{0}&{S_{32}}&{0}\end{array}\right] = \left[\begin{array}{ccc}{0}&{0}&{1}\\{1}&{0}&{0}\\{0}&{1}&{0}\end{array}\right] \]

En la Figura\(\PageIndex{3}\) (b) se muestra un circulador de microcinta, donde se puede colocar un disco de ferrita magnetizada en la parte superior de una\(\mathsf{Y}\) unión de microcinta para realizar una dirección preferencial de propagación de los campos EM [22]. El diseño requiere la elección del tamaño del disco de ferrita y el diseño del campo de polarización magnético apropiado. En ausencia del campo magnético de polarización, no se produce la función de circulación.

Además de las pérdidas de inserción y retorno, el rendimiento de un circulador se describe por su aislamiento, que es su pérdida de inserción en la dirección no deseada.

5.5.3 Aislamiento circular

El aislamiento de un circulador es la pérdida de inserción de lo que es el puerto de salida al puerto de entrada, es decir, en la dirección inversa. Haciendo referencia al circulador en la Figura\(\PageIndex{3}\) (a), si puerto\(\mathsf{1}\) es el puerto de entrada hay dos puertos de salida y así hay dos aislamientos iguales a la pérdida de retorno de puerto\(\mathsf{3}\) a puerto\(\mathsf{2}\), y de puerto\(\mathsf{2}\) a puerto\(\mathsf{1}\). El menor de estos es el aislamiento citado si solo se da un valor. Si este fuera un circulador ideal y el puerto\(\mathsf{2}\) está perfectamente emparejado, entonces el aislamiento sería infinito. Si\(\mathsf{2}\) el puerto no coincide perfectamente, entonces habrá un aislamiento finito de puerto\(\mathsf{3}\) a puerto\(\mathsf{1}\). Sin embargo, la fuente más común de aislamiento limitado es cuando el circulador no está perfectamente emparejado. Considera que el coeficiente de reflexión que busca en cada uno de los puertos del circulador es\(\Gamma\) y si el circulador está bien diseñado\(\Gamma ≪ 1\). Entonces los\(S\) parámetros del circulador son

\[\label{eq:3}\mathbf{S}=\left[\begin{array}{ccc}{\Gamma}&{\alpha}&{T}\\{T}&{\Gamma}&{\alpha}\\{\alpha}&{T}&{\Gamma}\end{array}\right] \]

donde\(T\) está el factor de transmisión y está cerca\(1\) para un buen circulador y la fuga,\(\alpha\), es pequeña. Si el circulador no tiene pérdidas entonces las condiciones unitarias, de las Ecuaciones (2.148) y (2.149) de [23], son

\[\begin{align}\label{eq:4}|T|^{2}+|\alpha|+|\Gamma|^{2}&=1 \\ \label{eq:5}\Gamma\alpha^{\ast}+T\Gamma^{\ast}+\alpha T^{\ast}&=0\to\alpha^{\ast}+T(\Gamma^{\ast}/\Gamma)+T^{\ast}(\alpha /\Gamma)=0\end{align} \]

Ya que\(\alpha\)\(\alpha\Gamma\) es pequeño es insignificante, por lo que Ecuación\(\eqref{eq:5}\) indica que\(|\alpha | = |\Gamma |\). Luego de la ecuación\(\eqref{eq:4}\)\(|T|^{2} = 1 − 2|\Gamma|^{2}\),, y se pueden escribir los\(S\) parámetros del circulador poco coincidente sin pérdidas

\[\label{eq:6}\mathbf{S}=\left[\begin{array}{ccc}{\Gamma}&{\Gamma}&{\sqrt{1-2|\Gamma|^{2}}}\\{\sqrt{1-2|\Gamma|^{2}}}&{\Gamma}&{\Gamma}\\{\Gamma}&{\sqrt{1-2|\Gamma|^{2}}}&{\Gamma}\end{array}\right] \]

Por lo tanto, incluso con la coincidencia externa ideal en el puerto\(\mathsf{2}\), el aislamiento es\(1/\Gamma\). La calidad de la coincidencia de un componente de microondas se especifica típicamente por su VSWR en los puertos. Así, el VSWR de un circulador indica el aislamiento que se puede esperar. Los circuladores reales tienen una pequeña cantidad de pérdida por lo que el aislamiento y VSWR cotizados para un circulador no se ajustarán exactamente a la situación sin pérdidas considerada aquí.

5.5.4 Aislador

Los aisladores son dispositivos que permiten el flujo de energía en una sola dirección. Hay dos tipos, uno basado en desplazamiento de campo y otro basado en resonancia giromagnética. Los aisladores de ferrita que explotan el desplazamiento de campo se basan en un circulador de tres puertos con uno de los puertos terminado en una carga coincidente. La Figura\(\PageIndex{3}\) (c) muestra un aislador de microcinta basado en un circulador de tres puertos. El disco en el centro es un material magnético tal como ferrita que cuando se magnetiza por un imán permanente o electroimán (que no se muestra) soporta preferentemente una onda EM giratoria en sentido contrario a las agujas del reloj. Por lo que la energía que ingresa a Puerto\(\mathsf{1}\) como una onda viajera se transfiere a la ferrita y emerge en Puerto\(\mathsf{2}\). Prácticamente nada de la energía emerge en Puerto\(\mathsf{3}\). Una señal de onda viajera aplicada en Port\(\mathsf{2}\) aparece en Port\(\mathsf{3}\), donde es absorbida en una terminación creada por material resistivo colocado en la parte superior de la microcinta. El material resistivo forma una línea de transmisión con pérdidas y, siempre que la sección de la línea con pérdidas sea lo suficientemente larga, no se refleja energía. Así, la potencia puede viajar de Puerto\(\mathsf{1}\) a Puerto\(\mathsf{2}\), pero no en sentido inverso. Un aislador se usa comúnmente para proteger la salida del equipo de señales reflejadas altas. Una versión de cuatro puertos puede implementar un duplexor en sistemas de radar y separar las señales recibidas y transmitidas en un transceptor.

En la Figura se muestra un aislador de microcinta de alta frecuencia derivado de un circulador\(\PageIndex{4}\). Las líneas de entrada y salida están en la parte superior y se redirigen debajo del disco. El disco se epoxida al sustrato de microcinta y se une un gran imán de polarización en la parte superior del disco. El tercer puerto se encuentra en la parte inferior de la figura.

Figura\(\PageIndex{4}\): Un aislador de microcinta que opera desde\(29\) hasta\(31.5\text{ GHz}\). Aislador en (b) tiene las dimensiones\(5\text{ mm}\times 6\text{ mm}\) y es\(6\text{ mm}\) alto. El aislador soporta\(2\text{ W}\) de potencia directa e inversa con un aislamiento\(18\text{ dB}\) y pérdida de inserción de\(1\text{ dB}\). Serie Renaissance 2W9, copyright Renaissance Electronics Corporation, utilizada con permiso.

Los aisladores también pueden explotar la resonancia giromagnética y luego se llaman aisladores de resonancia. Una rotación adecuada del campo magnético de RF en relación con la polarización magnética de CC resulta para una de las direcciones de propagación en una guía de ondas rectangular. En la frecuencia de resonancia giromagnética, la energía de RF se acopla a la red y la potencia de RF se absorbe para una dirección de propagación y en la otra dirección la señal de RF se ve poco afectada.

5.5.5 Filtro de paso de banda sintonizado por YIG

El efecto giromagnético también permite filtros de paso de banda variables muy nítidos. Un filtro sintonizado de itrio-hierro-granate (YIG) se muestra en la Figura\(\PageIndex{3}\) (d) y el resultado es que los Puertos\(\mathsf{1}\) y solo\(\mathsf{2}\) se acoplan a una frecuencia precisa determinada por el estado de magnetización de la esfera YIG. Con un electroimán que proporciona un campo magnético de CC, el campo magnético se puede variar y la frecuencia de resonancia, y por lo tanto la frecuencia de paso de banda, sintonizarse electrónicamente. Los analizadores de espectro de microondas a menudo usan un filtro sintonizado por YIG en la entrada del analizador.