7.5: Estudio de caso- Diseño de convertidor descendente de alto rango dinámico
- Page ID
- 85185
En esta sección se diseña un convertidor descendente en un receptor. Con la arquitectura y los módulos elegidos en la cascada de RF, las únicas cantidades que puede seleccionar el usuario son las ganancias de las etapas del amplificador. Si ajustar las ganancias no es suficiente para cumplir con los objetivos del sistema, entonces sería necesario elegir otros módulos o cambiar la arquitectura.
7.5.1 Arquitectura
Aquí se diseña un convertidor descendente con la arquitectura de la Figura 7.3.2 considerando solo las cuatro primeras etapas y utilizando el método de contribución balanceada para la asignación de la etapa inicial. El sistema opera\(1.5\text{ GHz}\) con un primer IF de\(250\text{ MHz}\) y un objetivo de\(\text{IIP3}\) diseño de\(0\text{ dBm}\) (es decir,\(\overline{\text{IIP3}}_{\text{dBm}}^{\text{T}} = 0\text{ dBm}\)) con un objetivo de cifra de ruido de\(10\text{ dB}\) (es decir,\(\overline{\text{NF}}^{\text{T}} = 10\text{ dB}\)). Las asignaciones de etapas iniciales para el ruido balanceado y las contribuciones IMD se muestran en la Tabla 7.4.1.
Las asignaciones de etapa que se muestran en la Tabla 7.4.1 cumplen exactamente con las especificaciones del objetivo, sin que una sola etapa contribuya más que el factor de ruido requerido o la no linealidad (distorsión) para cumplir con el objetivo. La ganancia de LNA es baja, lo que permite una reducción significativa en el mezclador requerido\(\text{IP3}\). En un sistema de RF generalmente el mezclador tiene el rendimiento de distorsión limitante por lo que cualquier cosa que se pueda hacer para reducir la linealidad requerida para un mezclador es ventajoso. La cifra de ruido de un mezclador también puede ser alta. Con esto en mente, el proceso de compensación en cascada del sistema y selección de parámetros reales del elemento continúa en las siguientes secciones. Es decir, la asignación de contribuciones balanceadas a cada etapa es un buen punto de partida inicial. Esto es seguido con una mayor optimización y compensaciones.
7.5.2 Diseño
El diseño continúa con una selección de módulos disponibles para etapas y variación continua pero limitada de los parámetros de etapa (a través del control de sesgo, por ejemplo). Se eligieron las siguientes etapas para las etapas (ver Figura 7.3.2): un amplificador MMIC para Stage\(2\) (parte NEC\(\text{UPC2745}\)) y un mezclador MMIC para Stage\(4\) (parte MCL\(\text{SYM-2500}\)). Se eligieron filtros resonadores dieléctricos de paso de banda para Etapas\(1\) y\(3\). En particular, se utilizó un filtro de paso de banda Chebychev de elemento grumoso afinado con\(0.1\text{ dB}\) ondulación at\(1.5\text{ GHz}\) para proporcionar pérdidas configurables en Stage\(3\) y esto resultó ser importante para establecer contribuciones de etapa equilibradas y mejorar el rango dinámico. Los parámetros de control continuo incluyen controlar la contribución del IMD del mezclador cambiando la ganancia de LNA (a través del control de polarización), cambiando el mezclador\(\text{IIP3}\) (variando el nivel de accionamiento LO) y reintonizando el\(3\) filtro Stage. Las contribuciones de ruido y distorsión de las etapas con la asignación de etapa inicial (de la Tabla 7.4.1), el rendimiento medido inicial y el diseño optimizado se muestran en las Figuras\(\PageIndex{1}\) y\(\PageIndex{2}\). La figura\(\PageIndex{3}\) representa el rango dinámico. Con base en el método de contribución balanceada, el SFDR se\(109.5\text{ dB}\) normaliza a un\(1\text{ Hz}\) ancho de banda. El valor inicial proporcionado por los dispositivos seleccionados es\(108\text{ dB}\). Después de la compensación apropiada y la pérdida ajustable en Stage\(3\), el rango dinámico logrado es\(111\text{ dB}\). Ahora se podría lograr el mismo diseño del sistema utilizando la asignación presupuestal inicialmente, pero con mucho mayor esfuerzo de diseño.
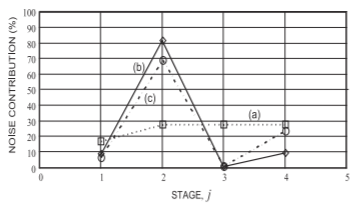
Figura\(\PageIndex{1}\): Contribución de la figura de ruido: (a) cálculo inicial de la contribución de la figura de ruido balanceada; (b) contribuciones medidas de cada etapa usando las asignaciones iniciales; y (c) contribuciones medidas finales después de alterar el sesgo, la pérdida de filtro y los niveles de accionamiento de LO del mezclador para mejorar el rango dinámico.
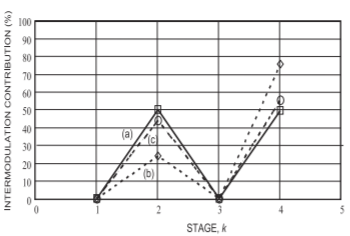
Figura\(\PageIndex{2}\): Contribución de intercepción de entrada (\(\text{IP3}\)): (a) cálculo inicial; (b) contribuciones medidas originales; y (c) desempeño final después de alteración de sesgo, impulso de LO y pérdida de filtro en la Etapa 3. Los ajustes finales en (c) condujeron al rango dinámico más alto del sistema.
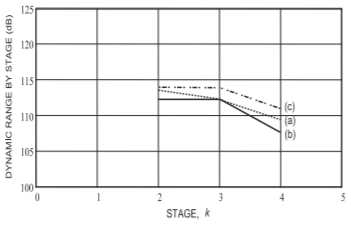
Figura\(\PageIndex{3}\): SFDR por etapa: (a) asignación inicial; (b) rendimiento inicial del sistema después de la selección de módulos pero antes de la optimización; y (c) rendimiento final después de establecer sesgo, impulso LO y pérdida de filtro en la Etapa 3.

