6.2: Comportamiento en estado estacionario de procesos irreducibles de Markov

Definición 6.2.1 (Procesos irreducibles de Markov) Un proceso irreducible de Markov es un proceso de Markov para el cual la cadena incrustada de Markov es irreducible (\(i.e.\), todos los estados están en la misma clase).

El análisis de este capítulo se restringe casi en su totalidad a procesos irreducibles de Markov. La razón de esta restricción no es que los procesos de Markov con múltiples clases de estados no sean importantes, sino que generalmente se pueden entender mejor mirando primero las cadenas incrustadas de Markov para las diversas clases que componen esa cadena general.

Haremos los mismos tipos de preguntas de estado estacionario para los procesos de Markov que preguntamos sobre las cadenas de Markov. En particular, ¿bajo qué condiciones hay un conjunto de probabilidades de estado estacionario,\(p_0, p_1, . . .\) con la propiedad de que para cualquier estado inicial dado\(i\), la fracción limitante de tiempo que pasa en un estado dado\(j\) es\(p_j\) con probabilidad 1? ¿Estas probabilidades también tienen la propiedad que\(p_j = \lim_{t\rightarrow \infty} \text{Pr}\{ X(t) = j | X_0 = i\}\)?

Encontraremos que el simple hecho de tener una cadena de Markov incrustada positivo-recurrente no es suficiente para asegurar que exista tal conjunto de probabilidades. También es necesario que las probabilidades de estado estacionario de la cadena incrustada {\(\pi_i; i\geq 0\)} y los parámetros de intervalo de retención {\(\nu_i;i\geq 0\)} satisfagan\(\sum_i \pi_i/\nu_i < \infty\). Interpretaremos esta última condición como afirmando que la tasa limitante a largo plazo a la que ocurren las transiciones debe ser estrictamente positiva. Finalmente mostraremos que cuando se cumplan estas condiciones, las probabilidades de estado estacionario para el proceso se relacionan con las de la cadena incrustada por

\[ p_j = \dfrac{\pi_j/\nu_j}{\sum_k\pi_k/\nu_k} \nonumber \]

Definición 6.2.2 Las probabilidades de proceso en estado estacionario,\(p_0, p_1, . . .\) para un proceso de Markov son un conjunto de números satisfactorios (6.2.1), donde {\(\pi_i; i\geq 0\)} y {\(\nu_i; i\geq 0\)} son las probabilidades de estado estacionario para la cadena incrustada y el holding- tasas de intervalo respectivamente.

Como se podría adivinar, el enfoque adecuado para responder a estas preguntas proviene de aplicar la teoría de la renovación a diversos procesos de renovación asociados con el proceso de Markov. Muchos de los resultados necesarios para esto ya se han desarrollado al observar el comportamiento en estado estacionario de las cadenas de Markov en el estado contable.

Comenzamos con un lema muy técnico que quizá parezca obvio, y el lector es bienvenido a ignorar la prueba hasta quizás cuestionar el tema más tarde. El lema no se restringe a procesos irreducibles, aunque solo lo usamos en ese caso.

Lema 6.2.1 Consideremos un proceso de Markov para el cual la cadena incrustada inicia en algún estado dado\(i\). Entonces los intervalos de tiempo de espera,\(U_1, U_2, . . .\) son todos rv. dejar\(M_i(t)\) ser el número de transiciones realizadas por el proceso hasta e incluyendo el tiempo\(t\). Luego con probabilidad 1 (WP1),

\[ \lim_{t\rightarrow\infty} M_i(t)=\infty \nonumber \]

Prueba: El primer intervalo de retención\(U_1\) es exponencial con tasa\(\nu_i > 0\), por lo que claramente es un rv (\(i.e.\), no defectuoso). En general el estado posterior a la (\(n-1\)) ésima transición tiene el PMF\(P^{n-1}_{ij}\), por lo que la función de distribución complementaria de\(U_n\) es

\[\begin{aligned} \text{Pr}\{U_n>u\} \quad &= \quad \lim_{k\rightarrow \infty} \sum^k_{j=1} P^{n-1}_{ij} \exp (-\nu_ju) \\ &\leq \quad \sum^k_{j=1} P^{n-1}_{ij} \exp(-\nu_j u)+ \sum^{\infty}_{j=k+1} P^{n+1}_{ij} \quad \text{for every } k \end{aligned} \nonumber \]

Para cada uno\(k\), la primera suma anterior se acerca a 0 con el aumento\(u\) y la segunda suma se acerca a 0 con el aumento\(k\) por lo que el límite como\(u \rightarrow\infty\) debe ser 0 y\(U_n\) es un rv

De ello se deduce que cada uno\(S_n = U_1 + · · · + U_n\) es también un rv. Ahora {\(S_n; n\geq 1\)} es la secuencia de épocas de llegada en un proceso de llegada, así que tenemos la igualdad establecida {\(S_n \leq t\)} = {\(M_i(t)\geq n\)} para cada elección de\(n\). Ya que\(S_n\) es un rv, tenemos\(\lim_{t\rightarrow \infty} \text{Pr}\{S_n \leq t\} = 1\) para cada uno\(n\). Así\(\lim_{t\rightarrow \infty} \text{Pr}\{M_i(t)\geq n\} = 1\) para todos\(n\). Esto significa que el conjunto de puntos de muestreo\(\omega\) para los cuales\(\lim_{t\rightarrow\infty} M_i(t, \omega) < n\) tiene probabilidad 0 para todos\(n\), y por lo tanto\(\lim_{t\rightarrow \infty} M_i(t, \omega) = \infty\) WP1.

\(\square\)

Renovaciones en entradas sucesivas a un Estado determinado

Para un proceso irreducible de Markov con\(X_0 = i\), deja\(M_{ij} (t)\) ser el número de transiciones en estado a\(j\) lo largo del intervalo\((0,t]\). Queremos encontrar cuándo se trata de un proceso de recuento de renovación retrasada. Es claro que la secuencia de épocas en las que\(j\) se ingresa estado forman puntos de renovación, ya que forman puntos de renovación en la cadena incrustada de Markov y los intervalos de retención entre transiciones dependen únicamente del estado actual. Las preguntas son si la primera entrada al estado\(j\) debe ocurrir dentro de algún tiempo finito, y si las recurrencias a\(j\) deben ocurrir dentro del tiempo finito. El siguiente lema responde a estas preguntas para el caso donde la cadena incrustada es recurrente (ya sea recurrente positiva o recurrente nula).

_______________________________________________________________________________________________

Lema 6.2.2. Considere un proceso de Markov con una cadena incrustada recurrente irreducible {\(X_n; n \geq 0\)}. Dado\(X_0 = i\), sea {\(M_{ij} (t); t\geq 0\)} el número de transiciones a un estado dado\(j\) en el intervalo\((0,t]\). Entonces {\(M_{ij} (t); t\geq 0\)} es un proceso de conteo de renovación retrasada (o un proceso ordinario de conteo de renovación si\(j = i\)).

Prueba: Dado\(X_0 = i\), deja\(N_{ij} (n)\) ser el número de transiciones a estado\(j\) que ocurren en la cadena incrustada de Markov por la\(n^{th}\) transición de la cadena incrustada. De Lemma 5.1.4, {\(N_{ij} (n); n\geq 0\)} es un proceso de renovación retrasada, así que a partir de Lemma 4.8.2,\(\lim_{n\rightarrow \infty} N_{ij} \ref{n} = \infty\) con probabilidad 1. Tenga en cuenta que\(M_{ij} \ref{t} = N_{ij} (M_i(t))\), donde\(M_i(t)\) está el número total de transiciones de estado (entre todos los estados) en el intervalo\((0,t]\). Así, con probabilidad 1,

\[ \lim_{t\rightarrow \infty} M_{ij}(t)=\lim_{t\rightarrow\infty} N_{ij}(M_i(t))=\lim_{n\rightarrow\infty}N_{ij}(n) = \infty \nonumber \]

donde hemos utilizado Lemma 6.2.1, que afirma que\(\lim_{t\rightarrow\infty} M_i(t) = \infty\) con probabilidad 1.

De ello se deduce que el intervalo\(W_1\) hasta la primera transición a estado\(j\), y el intervalo posterior\(W_2\) hasta la siguiente transición a estado\(j\), son ambos finitos con probabilidad 1. Los intervalos posteriores tienen la misma distribución que\(W_2\), y todos los intervalos son independientes, por lo que {\(M_{ij} (t); t \geq 0\)} es un proceso de renovación retardada con intervalos entre renovaciones {\(W_k; k\geq 1\)}. Si\(i = j\), entonces todos\(W_k\) están distribuidos de manera idéntica y tenemos un proceso ordinario de renovación, completando la prueba.

\(\square \)

Los intervalos entre renovaciones\(W_2, W_3, . . .\) para {\(M_{ij} (t); t\geq 0\)} anteriores son IID rv no negativos bien definidos cuya distribución depende de\(j\) pero no\(i\). O tienen una expectativa como número finito o tienen una expectativa infinita. En cualquier caso, esta expectativa se denota como\(\mathsf{E} [W(j)] = \overline{W}(j)\). Este es el tiempo medio entre las sucesivas entradas a estado\(j\), y veremos más adelante que en algunos casos este tiempo medio puede ser infinito.

Fracción limitante de tiempo en cada estado

Para estudiar la fracción de tiempo pasado en estado\(j\), definimos un proceso de renovación-recompensa retrasado, basado en {\(M_{ij} (t); t \geq 0\)}, para el cual se acumula recompensa unitaria siempre que el proceso está en estado\(j\). Eso es (dado\(X_0 = i\)),\(R_{ij} \ref{t} = 1\) cuándo\(X(t) = j\) y de\(R_{ij} \ref{t} = 0\) otra manera. (ver Figura 6.7). Dado que la transición\(n-1\) de la cadena incrustada entra en estado\(j\), el intervalo\(U_n\) es exponencial con tasa\(\nu_j\), entonces\(\mathsf{E} [U_n | X_{n-1}=j] = 1/\nu_j\).

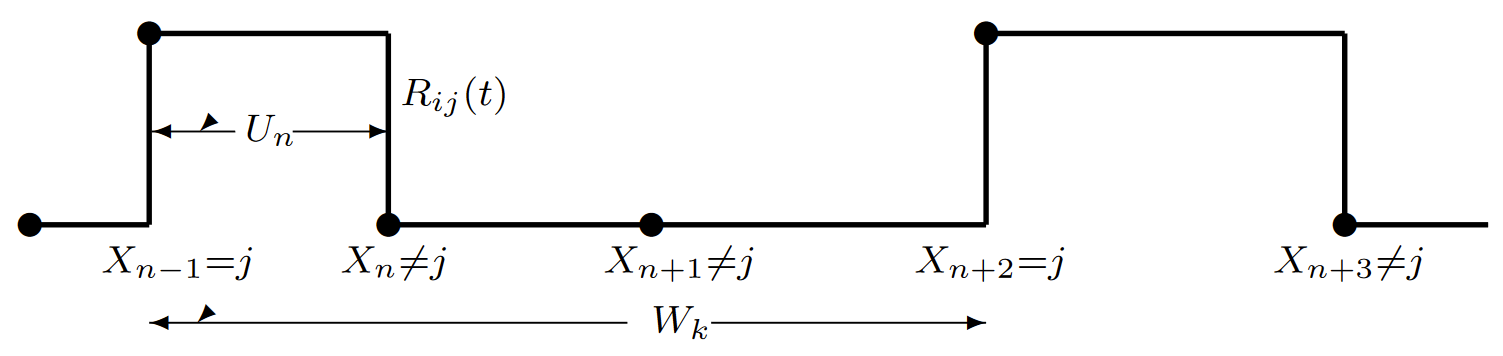
Figura 6.7: El proceso retrasado de renovación-recompensa {\(R_{ij} (t); t \geq 0\)} para cualquier momento en estado\(j\). La recompensa es una siempre que el proceso esté en estado\(j\),\(i.e.\),\(R_{ij}(t)=\mathbb{I}_{\{X(t)=j\}}\). Se produce una renovación en cada entrada al estado\(j\), por lo que la recompensa inicia en cada entrada de ese tipo y continúa hasta una transición de estado, asumiendo que ingresa a un estado distinto al\(j\). La recompensa cesa entonces hasta la próxima renovación,\(i.e.\), la siguiente entrada al estado\(j\). La figura ilustra el intervalo interrenovaciones\(k\) th, de duración\(W_k\), que se supone que inicia en la transición de estado\(n-1\) st. El intervalo esperado sobre el cual se acumula una recompensa es\(\nu_j\) y es la duración esperada del intervalo entre renovaciones es\(\overline{W}(j)\).

Dejar\(p_j (i)\) ser la fracción limitante de tiempo promedio del tiempo pasado en estado\(j\). Veremos más adelante que tal límite existe WP1, del que el límite no depende\(i\), y que es igual a la probabilidad de estado estacionario\(p_j\) en (6.2.1). Ya que\(\overline{U}(j) = 1/\nu_j\), los Teoremas 4.4.1 y 4.8.4, para los procesos ordinarios y retrasados de renovación-recompensa respectivamente, establecen que ¹

\[ \begin{align} p_j(i) \quad &= \quad \lim_{t\rightarrow \infty} \dfrac{\int^t_0 R_{ij}(\tau)d\tau}{t} \quad \text{WP1} \\ &= \quad \dfrac{\overline{U}(j)}{\overline{W}(j)} \quad = \quad \dfrac{1}{\nu_j\overline{W}(j)} \end{align} \nonumber \]

Esto demuestra que el promedio de tiempo limitante\(p_j (i)\),, existe con probabilidad 1 y es independiente del estado inicial\(i\). Mostramos posteriormente que es la probabilidad de proceso en estado estacionario dada por (6.2.1). También podemos investigar el límite, como\(t \rightarrow \infty\), de la probabilidad de que\(X(t) = j\). Esto es igual a\(\lim_{t\rightarrow \infty} \mathsf{E} [R(t)]\) para el proceso de renovación-recompensa anterior. Debido a los intervalos exponenciales de retención, los tiempos de inter-renovación no son aritméticos, y a partir del teorema de Blackwell, en forma de (4.105),

\[ \lim_{t\rightarrow\infty} \text{Pr}\{X(t)=j \} = \dfrac{1}{\nu_j\overline{W}(j)} = p_j(i) \nonumber \]

Resumimos estos resultados en el siguiente lema.

Lema 6.2.3 Considerar un proceso irreducible de Markov con una cadena de Markov incrustada recurrente comenzando en\(X_0 = i\). Entonces con probabilidad 1, el promedio de tiempo limitante en estado\(j\) viene dado por\(p_j \ref{i} = \dfrac{1}{\nu_j\overline{W}(j)}\). Este es también el límite, como\(t \rightarrow \infty\), de\(\text{Pr}\{ X(t) = j\}\).

Encontrar\(\{p_j (i); j\geq 0\}\) en términos de\(\{\pi_j ; j\geq 0\}\)

A continuación debemos expresar el tiempo medio de inter-renovación,\(\overline{W}(j)\), en términos de cantidades más accesibles que nos permitan demostrar que\(p_j \ref{i} = p_j\) dónde\(p_j\) está la probabilidad de proceso de estado estacionario de la Definición 6.2.2. Ahora asumimos que la cadena incrustada no solo es recurrente sino también positiva recurrente con probabilidades de estado estacionario {\(\pi_j ; j\geq 0\)}. Seguimos asumiendo un estado de inicio dado\(X_0 = i\). Aplicando la ley fuerte para procesos de renovación retardada (Teorema 4.8.1) al proceso de Markov,

\[ \lim_{t\rightarrow\infty} M_{ij}(t)/t=1/\overline{W}(j) \qquad \text{WP1} \nonumber \]

Como antes,\(M_{ij} \ref{t} = N_{ij} (M_i(t))\). Dado que\(\lim_{t\rightarrow\infty} M_i(t) = \infty\) con probabilidad 1,

\[ \lim_{t\rightarrow\infty}\dfrac{M_{ij}(t)}{M_i(t)} = \lim_{t\rightarrow\infty}\dfrac{N_{ij}(M_i(t))}{M_i(t)} = \lim_{n\rightarrow\infty} \dfrac{N_{ij}(n)}{n}=\pi_j \qquad \text{WP1} \nonumber \]

En el último paso, aplicamos la misma ley fuerte a la cadena incrustada. Combinando (6.2.6) y (6.2.7), las siguientes igualdades se mantienen con probabilidad 1.

\[ \begin{align} \dfrac{1}{\overline{W}(j)} \quad &= \quad \lim_{t\rightarrow\infty}\dfrac{M_{ij}(t)}{t} \nonumber \\ &= \quad \lim_{t\rightarrow\infty} \dfrac{M_{ij}(t)}{M_i(t)}\dfrac{M_i(t)}{t} \nonumber \\ &= \quad \pi_j \lim_{t\rightarrow \infty} \dfrac{M_i(t)}{t} \end{align} \nonumber \]

Esto nos dice que\(\overline{W}(j)\pi_j\) es lo mismo para todos\(j\). También, ya que\(\pi_j > 0\) para una cadena recurrente positiva, nos dice que si\(\overline{W}(j) < \infty\) por un estado\(j\), es finita para todos los estados. También estos tiempos de recurrencia esperados son finitos si y solo si\(\lim_{t\rightarrow\infty} M_i(t)/t > 0\). Por último, dice implícitamente que\(\lim_{t\rightarrow\infty}M_i(t)/t\) existe WP1 y tiene el mismo valor para todos los estados iniciales\(i\).

Queda relativamente poco por hacer, y el siguiente teorema hace la mayor parte de ello.

Teorema 6.2.1. Considere un proceso irreducible de Markov con una cadena de Markov incrustada recurrente positiva. Sea {\(\pi_j ; j\geq 0\)} las probabilidades de estado estacionario de la cadena incrustada y deje\(X_0 = i\) ser el estado inicial. Entonces, con probabilidad 1, la fracción de tiempo promedio limitante del tiempo pasado en cualquier estado arbitrario\(j\) es la probabilidad de proceso de estado estacionario en (6.2.1)\(i.e.\),

\[ p_j(i)=p_j=\dfrac{\pi_k/\nu_j}{\sum_k\pi_k/\nu_k} \nonumber \]

El tiempo esperado entre retornos al estado\(j\) es

\[ \overline{W}(j) = \dfrac{\sum_k \pi_k/\nu_k}{\pi_j} \nonumber \]

y la velocidad límite a la que tienen lugar las transiciones es independiente del estado inicial y dada por

\[ \lim_{t\rightarrow\infty} \dfrac{M_i(t)}{t} = \dfrac{1}{\sum_k\pi_k/\nu_k} \qquad \text{WP1} \nonumber \]

Discusión: Recordemos que se\(p_j (i)\) definió como un promedio de tiempo WP1, y vimos antes que este promedio de tiempo existía con un valor independiente de\(i\). El teorema establece que este promedio de tiempo (y el promedio de conjunto limitante) viene dado por las probabilidades de proceso de estado estacionario en (6.2.1). Así, después de la prueba, podemos dejar de distinguir estas cantidades.

A nivel superficial, el teorema es casi obvio por lo que hemos hecho. En particular, sustituyendo (6.2.8) por (6.2.3), vemos que

\[ p_j(i) = \dfrac{\pi_j}{\nu_j} \lim_{t\rightarrow\infty} \dfrac{M_i(t)}{t} \qquad \text{WP1} \nonumber \]

Ya que\(p_j \ref{i} = \lim_{t\rightarrow\infty} \text{Pr}\{ X(t) = j\}\), y como\(X(t)\) está en algún estado en todo momento, conjeturaríamos (e incluso insistiremos si no seguimos leyendo) eso\(\sum_j p_j \ref{i} = 1\). Añadiendo esa condición para normalizar (6.2.10), obtenemos (6.2.9), y (6.2.10) y (6.2.11) siguen inmediatamente. El problema es que si\(\sum_j \pi_j/\nu_j = \infty\), entonces (6.2.9) dice eso\(p_j = 0\) para todos\(j\), y (6.2.11) dice que\(\lim M_i(t)/t = 0\),\(i.e.\), el proceso 'se cansa' con el aumento\(t\) y la tasa de transiciones disminuye hacia 0. La prueba más bien técnica a seguir trata de estos límites con más cuidado

Prueba: Hemos visto en (6.2.8) que\(\lim_{t\rightarrow\infty} M_i(t)/t\) es igual a una constante, digamos\(\alpha\), con probabilidad 1 y que esta constante es la misma para todos los estados iniciales\(i\). Primero consideramos el caso donde\(\alpha > 0\). En este caso, desde (6.2.8),\(\overline{W}(j) < \infty\) para todos\(j\). Al elegir cualquier entero dado\(j\) y cualquier número entero positivo\(\ell\), considere un proceso de renovación-recompensa con renovaciones en las transiciones a\(j\) y una recompensa\(R^{\ell}_{ij} \ref{t} = 1\) cuándo\(X(t) \leq \ell\). Esta recompensa es independiente\(j\) e igual a\(\sum^{\ell}_{k=1} R_{ik}(t)\). Así, desde (6.2.3), tenemos

\[ \lim_{t\rightarrow\infty} \dfrac{\int^t_0 R^{\ell}_{ij} (\tau) d\tau}{t} = \sum^{\ell}_{k=1} p_k(i) \nonumber \]

Si dejamos\(\mathsf{E} \left[ R^{\ell}_j\right] \) ser la recompensa esperada a lo largo de un intervalo de renovación, entonces, a partir del Teorema 4.8.4,

\[\lim_{t\rightarrow\infty}\dfrac{\int^t_0 R^{\ell}_{ij}(\tau)d\tau}{t} = \dfrac{\mathsf{E}\left[ R^{\ell}_j \right] }{\overline{U}_j} \nonumber \]

Tenga en cuenta que\(\mathsf{E} \left[ R^{\ell}_j\right]\) lo anterior es no decreciente en\(\ell\) y va al límite\(\overline{W}(j)\) como\(\ell \rightarrow \infty\). Así, combinando (6.2.11) y (6.2.14), vemos que

\[ \lim_{\ell \rightarrow\infty} \sum^{\ell}_{k=1} p_k(i) =1 \nonumber \]

Con esta relación añadida, siguen (6.2.9), (6.2.10) y (6.2.11) como en la discusión. Esto completa la prueba para el caso donde\(\alpha > 0\).

Para el caso restante, donde\(\lim_{t\rightarrow\infty} M_i(t)/t = \alpha = 0\), (6.2.8) muestra eso\(\overline{W}(j) = \infty\) para todos\(j\) y (6.2.12) luego muestra eso\(p_j \ref{i} = 0\) para todos\(j\). Damos una prueba guiada en el Ejercicio 6.6 que\(\alpha = 0\), para, debemos tener\(\sum_i \pi_i/\nu_i = \infty\). De ello se deduce que (6.2.9), (6.2.10) y (6.2.11) están todos satisfechos.

\(\square\)

Esto ha sido una prueba bastante difícil de algo que podría parecer casi obvio para ejemplos simples. Sin embargo, el hecho de que estos promedios de tiempo sean válidos sobre todos los puntos de muestra con probabilidad 1 no es obvio y el hecho de que\(\pi_j\overline{W}(j)\) sea independiente de ciertamente no\(j\) es obvio.

Lo más sutil aquí, sin embargo, es que si\(\sum_i \pi_i/\nu_i = \infty\), entonces\(p_j = 0\) para todos los estados\(j\). Esto es extraño porque las probabilidades de estado promedio de tiempo no se suman a 1, y también extraño porque la cadena incrustada de Markov continúa haciendo transiciones, y estas transiciones, en estado estacionario para la cadena de Markov, ocurren con las probabilidades\(\pi_i\). El Ejemplo 6.2.1 y el Ejercicio 6.3 dan una idea de esto. Se puede obtener un poco de conocimiento adicional al observar la cadena incrustada de Markov que comienza en estado estacionario\(i.e.\),, con probabilidades {\(\pi_i; i\geq 0\)}. Dado\(X_0 = i\), el tiempo esperado para una transición es\(1/\nu_i\), por lo que es el tiempo incondicional esperado a una transición\(\sum_i \pi_i/\nu_i\), que es infinito para el caso en consideración. Este no es un fenómeno que pueda entenderse fácilmente de manera intuitiva, pero el Ejemplo 6.2.1 y el Ejercicio 6.3 ayudarán.

Resolver las probabilidades de proceso en estado estacionario directamente

Volvamos al caso donde\(\sum_k \pi_k/\nu_k < \infty\), que es el caso de prácticamente todas las aplicaciones. Hemos visto que un proceso de Markov puede especificarse en términos de las transiciones de tiempo\(q_{ij} = \nu_iP_{ij}\), y es útil expresar las ecuaciones de estado estacionario para\(p_j\) directamente en términos de\(q_{ij}\) más que indirectamente en términos de la cadena incrustada. Como preludio útil a esto, primero expresamos el\(\pi_j\) en términos de la\(p_j\). Denotar\(\sum_k \pi_k/\nu_k\) como\(\beta< \infty\). Entonces, de (6.2.9)\(p_j = \pi_j/\nu_j\), así\(\pi_j = p_j\nu_j \beta\). Expresando esto junto con la normalización\(\sum_k \pi_k = 1\), obtenemos

\[ \pi_i = \dfrac{p_i\nu_i}{\sum_k p_k\nu_k} \nonumber \]

Así,\(\beta= 1/ \sum_k p_k\nu_k\), tan

\[\sum_k \pi_k/\nu_k = \dfrac{1}{\sum_k p_k \nu_k} \nonumber \]

Ahora podemos sustituir\(\pi_i\) según lo dado por (6.2.15) en las ecuaciones de estado estacionario para la cadena incrustada de Markov\(i.e.\),\(\pi_j = \sum_i \pi_iP_{ij}\) para todos\(j\), obteniendo

\[ p_j\nu_j = \sum_i p_i\nu_i P_{ij} \nonumber \]

para cada estado\(j\). Dado que\(\nu_iP_{ij} = q_{ij} \),

\[ p_j\nu_j = \sum_i p_iq_{ij}; \qquad \sum_ip_i=1 \nonumber \]

Este conjunto de ecuaciones se conoce como las ecuaciones de estado estacionario para el proceso de Markov. La condición de normalización\(\sum_i p_i = 1\) es consecuencia de (6.2.16) y también de (6.2.9). La ecuación (6.2.17) tiene una buena interpretación en que el término a la izquierda es la tasa de estado estacionario a la que ocurren las transiciones fuera de estado\(j\) y el término a la derecha es la velocidad a la que las transiciones ocurren en estado\(j\). Dado que el número total de entradas a\(j\) debe diferir como máximo en 1 de las\(j\) salidas de cada ruta de muestreo, esta ecuación no es sorprendente.

La cadena incrustada es recurrente positiva, por lo que sus ecuaciones de estado estacionario tienen una solución única con todas\(\pi_i > 0\). Así (6.2.17) también tiene una solución única con todo\(p_i > 0\) bajo la condición añadida que\(\sum_i \pi_i/\nu_i < \infty\). Sin embargo, nos gustaría resolver (6.2.17) directamente sin preocuparnos por la cadena incrustada

Si encontramos una solución a (6.2.17), sin embargo, y si\(\sum_i p_i\nu_i < \infty\) en esa solución, entonces el conjunto correspondiente de\(\pi_i\) from (6.2.15) debe ser la solución de estado estacionario única para la cadena incrustada. Así, la solución para\(p_i\) debe ser la correspondiente solución en estado estacionario para el proceso de Markov. Esto se resume en el siguiente teorema.

Teorema 6.2.2. Asumir un proceso irreducible de Markov y dejar que {\(p_i; i\geq 0\)} sea una solución a (6.2.17). Si\(\sum_i p_i\nu_i < \infty\), entonces, primero, esa solución es única, segundo, cada uno\(p_i\) es positivo, y tercero, la cadena incrustada de Markov es positiva recurrente con probabilidades de estado estacionario satisfactorias (6.2.15). Además, si la cadena incrustada es recurrente positiva, y\(\sum_i \pi_i/\nu_i < \infty\) entonces el conjunto de\(p_i\) satisfactorios (6.2.9) es la solución única a (6.2.17).

aproximación de tiempo muestreado de nuevo

Para una visión alternativa de las probabilidades {\(p_i; i\geq 0\)}, considere el caso especial (pero el caso típico) donde se acoplan las tasas de transición {\(\nu_i; i\geq 0\)}. Considere la aproximación de tiempo muestreado al proceso para un tamaño de incremento dado\(\delta \leq [\max_i \nu_i]^{-1}\) (ver Figura 6.6). Sea {\(p_i(\delta); i\geq 0\)} el conjunto de probabilidades de estado estacionario para la cadena de tiempo muestreada, asumiendo que existen. Estas probabilidades de estado estacionario satisfacen

\[ p_j(\delta) = \sum_{i\neq j} p_i(\delta)q_{ij}\delta+p_j(\delta)(1-\nu_j\delta); \quad p_j(\delta) \geq 0; \quad \sum_j p_j(\delta) =1 \nonumber \]

La primera ecuación simplifica a\(p_j (\delta)\nu_j = \sum_{i\neq j} p_i(\delta)q_{ij} \), que es la misma que (6.2.17). De ello se deduce que las probabilidades de estado estacionario {\(p_i; i\geq 0\)} para el proceso son las mismas que las probabilidades de estado estacionario {\(p_i(\delta); i\geq 0\)} para la aproximación de tiempo muestreado. Tenga en cuenta que esto no es una aproximación;\(p_i(\delta)\) es exactamente igual a\(p_i\) para todos los valores de\(\delta \leq 1/ \sup_i \nu_i\). Veremos más adelante que la dinámica de un proceso de Markov no está tan bien modelada por la aproximación del tiempo muestreado excepto en el límite\(\delta\rightarrow 0\).

Casos patológicos

Ejemplo 6.2.1 (Tasa de Transición Cero) Considere el proceso de Markov con una cadena incrustada positivo-recurrente en la Figura 6.8. Esto modela una variación de una cola M/M/1 en la que el servidor se vuelve cada vez más traqueteado y lento a medida que la cola se acumula, y los clientes se desaniman casi por igual de entrar. La deriva descendente en las transiciones es más que superada por la desaceleración en estados numerados grandes. Las transiciones continúan ocurriendo, pero el número de transiciones por unidad de tiempo va a 0 con el aumento del tiempo. Aunque la cadena incrustada tiene una solución de estado estacionario, el proceso no puede considerarse que tenga ningún tipo de estado estacionario. El ejercicio 6.3 da una idea adicional de este tipo de situaciones.

Figura 6.8: El proceso de Markov para una variación en M/M/1 donde las llegadas y los servicios se vuelven más lentos con el aumento del estado. Cada nodo\(i\) tiene una tasa\(\nu_i=2^{-i}\). Las probabilidades de transición de cadena incrustadas son\(P_{i,i+1}=0.4\) para\(i\geq 1\) y\(P_{i,i-1}=0.6\) para\(i\geq 1\), asegurando así que la cadena incrustada de Markov sea recurrente positiva. Obsérvese eso\(q_{i,i+1}> q_{i+1,i}\), asegurando así que el proceso de Markov se desvía hacia la derecha.

También es posible que (6.2.17) tenga una solución para {\(p_i; i\geq 0\)} con\(\sum_i p_i = 1\), pero\(\sum_i p_i\nu_i = \infty\). Esto no es posible para una cadena incrustada recurrente positiva, pero es posible tanto si la cadena incrustada de Markov es transitoria como si es recurrente nula. Una cadena transitoria significa que existe una probabilidad positiva de que la cadena incrustada nunca regrese a un estado después de abandonarla, y por lo tanto no puede haber ningún tipo de comportamiento sensato en estado estacionario para el proceso. Estos procesos se caracterizan por tasas de transición arbitrariamente grandes desde los diversos estados, y estos permiten que el proceso transite por un número infinito de estados en un tiempo finito.

Los procesos para los que existe una probabilidad distinta de cero de pasar por un número infinito de estados en un tiempo finito se denominan irregulares. Los ejercicios 6.8 y 6.7 dan una idea de los procesos irregulares. El ejercicio 6.9 da un ejemplo de un proceso que no es irregular, pero para el cual (6.2.17) tiene una solución con\(\sum_i p_i = 1\) y la cadena incrustada de Markov es nula recurrente. Limitamos nuestra atención en lo que sigue a cadenas irreducibles de Markov para las cuales (6.2.17) tiene una solución,\(\sum p_i = 1\), y\(\sum p_i\nu_i < \infty\). Esto es un poco más restrictivo de lo necesario, pero los procesos para los cuales\(\sum_i p_i\nu_i = \infty\) (ver Ejercicio 6.9) no son muy robustos.

_________________________________________________

1. Los teoremas 4.4.1 y 4.8.4 no cubren el caso donde\(\overline{W} \ref{j} = \infty\), pero, dado que la recompensa esperada por intervalo de renovación es finita, no es difícil de verificar (6.2.3) en ese caso especial.