2.1: Introducción a los procesos de Poisson

Un proceso de Poisson es un proceso estocástico simple y ampliamente utilizado para modelar los tiempos en que las llegadas ingresan a un sistema. Es en muchos sentidos la versión en tiempo continuo del proceso Bernoulli la que se describió en la Sección 1.3.5. Para el proceso de Bernoulli, las llegadas pueden ocurrir solo en múltiplos enteros positivos de algún tamaño de incremento dado (a menudo tomado como 1). Sección 1.3.5 caracterizó el proceso por una secuencia de variables aleatorias binarias IID (rv)\(Y_{1}, Y_{2}, \ldots\), donde\(Y_{i}=1\) indica una llegada al incremento\(i\) y de\(Y_{i}=0\) otra manera. Observamos (sin ninguna prueba cuidadosa) que el proceso también podría caracterizarse por la secuencia de tiempos de interllegada. Estos tiempos de interllegada están distribuidos geométricamente IID rv.

Para el proceso de Poisson, las llegadas pueden ocurrir en momentos positivos arbitrarios, y la probabilidad de una llegada en cualquier instante en particular es 0. Esto significa que no hay una manera muy limpia de describir un proceso de Poisson en términos de la probabilidad de una llegada en un instante dado. Es más conveniente definir un proceso de Poisson en términos de la secuencia de tiempos de interllegada\(X_{1}, X_{2}, \ldots\), los cuales se definen como IID. Antes de hacer esto, describimos los procesos de llegada con un poco más de detalle.

Procesos de llegada

Un proceso de llegada es una secuencia de rv crecientes,\(0<S_{1}<S_{2}<\cdots\), donde ¹\(S_{i}<S_{i+1}\) significa que\(S_{i+1}-S_{i}\) es un rv positivo, es decir, un rv\(X\) tal que\(\mathrm{F}_{X}(0)=0\). Los rv\(S_{1}, S_{2}, \ldots\), se denominan épocas de llegada (la palabra tiempo es algo sobreutilizada en este tema) y representan los tiempos en los que ocurre algún fenómeno repetitivo. Tenga en cuenta que el proceso comienza en el tiempo 0 y que las llegadas múltiples no pueden ocurrir simultáneamente (el fenómeno de llegadas masivas puede manejarse mediante la simple extensión de asociar un rv entero positivo a cada llegada). A veces vamos a permitir llegadas simultáneas o llegadas en el tiempo 0 como eventos de probabilidad cero, pero estos pueden ser ignorados. Para especificar completamente el proceso por la secuencia\(S_{1}, S_{2}, \ldots\) de rv, es necesario especificar la distribución conjunta de las subsecuencias\(S_{1}, \ldots, S_{n}\) para todos\(n>1\).

Aunque nos referimos a estos procesos como procesos de llegada, también podrían modelar salidas de un sistema, o cualquier otra secuencia de incidentes. Si bien es bastante común, sobre todo en el campo de la simulación, referirse a incidentes o llegadas como eventos, aquí lo evitaremos. La\(n\) época de llegada\(S_{n}\) es un rv y\(\left\{S_{n} \leq t\right\}\), por ejemplo, es un evento. Esto haría confuso referirse a la\(n\) llegada misma como un evento.

Figura 2.1: Una función muestral de un proceso de llegada y sus épocas de llegada\(\left\{S_{1}, S_{2}, \ldots\right\}\), sus intervalos\(\left\{X_{1}, X_{2}, \ldots\right\}\) entre llegadas y su proceso de conteo\(\{N(t) ; t>0\}\)

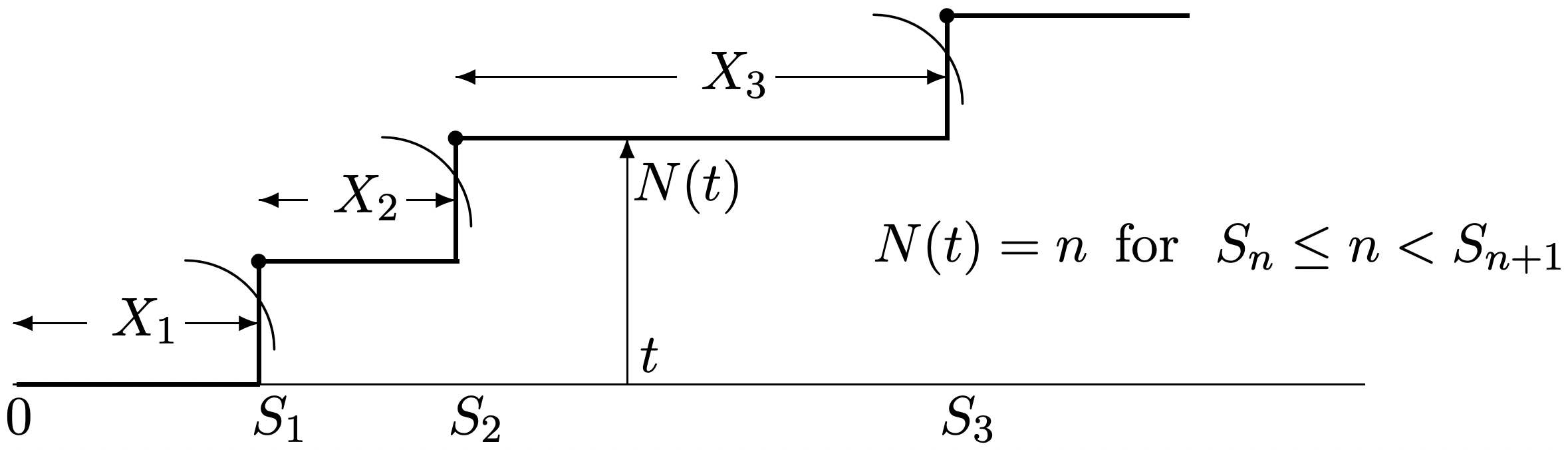
Como se ilustra en la Figura 2.1, cualquier proceso de llegada también puede especificarse mediante dos procesos estocásticos alternativos. La primera alternativa es la secuencia de tiempos de interllegada, X_ {1}, X_ {2},\ ldots,. Estos son rv positivos definidos en términos de las épocas de llegada por\(X_{1}=S_{1}\) y\(X_{i}=S_{i}-S_{i-1}\) para\(i>1\). De igual manera, dado el\(X_{i}\), las épocas de llegada\(S_{i}\) se especifican como

\[S_{n}=\sum_{i=1}^{n} X_{i}\label{2.1} \]

Así, la distribución conjunta de\(X_{1}, \ldots, X_{n}\) para todos\(n>1\) es suciente (en principio) para especificar el proceso de llegada. Dado que los tiempos de interllegada son IID en la mayoría de los casos de interés, suele ser mucho más fácil especificar la distribución conjunta de la\(X_{i}\) que de la\(S_{i}\).

La segunda alternativa para especificar un proceso de llegada es el proceso de conteo\(N(t)\), donde para cada uno\(t>0\), el rv\(N(t)\) es el número de llegadas ² hasta e incluyendo el tiempo\(t\).

El proceso de conteo\(\{N(t) ; t>0\}\), ilustrado en la Figura 2.1, es una familia infinitamente infinita de rv\(\{N(t) ; t>0\}\) donde\(N(t)\), para cada uno\(t>0\), es el número de llegadas en el intervalo\((0, t]\), si los puntos finales están incluidos en estos intervalos es a veces importante, y usamos paréntesis para representar intervalos sin puntos finales y corchetes para representar la inclusión del punto final. Así\((a, b)\) denota el intervalo\(\{t: a<t<b\}\), y\((a, b]\) denota\(\{t: a<t \leq b\}\). Los rv de conteo\(N(t)\) para cada uno\(t>0\) se definen entonces como el número de llegadas en el intervalo\((0, t]\). \(N(0)\)se define como 0 con probabilidad 1, lo que significa, como antes, que estamos considerando solo llegadas en momentos estrictamente positivos.

El proceso de conteo\(\{N(t) ; t>0\}\) para cualquier proceso de llegada tiene las propiedades que\(N(\tau) \geq N(t)\) para todos\(\tau \geq t>0\) (es decir,\(N(\tau)-N(t)\) es una variable aleatoria no negativa).

Para cualquier entero\(n \geq 1\) y tiempo dados\(t>0\), la época de llegada\(n\) th\(S_{n}\), y la variable aleatoria de conteo,\(N(t)\), están relacionados por

\[\left\{S_{n} \leq t\right\}=\{N(t) \geq n\}\label{2.2} \]

Para ver esto, tenga en cuenta que\(\left\{S_{n} \leq t\right\}\) es el suceso de que la enésima llegada ocurre por tiempo\(t\). Este evento implica que\(N(t)\), el número de llegadas por tiempo\(t\), debe ser al menos\(n\); es decir, implica el evento\(\{N(t) \geq n\}\). De igual manera\(\left\{S_{n} \leq t\right\}\),\(\{N(t) \geq n\}\) implica, cediendo la igualdad en (2.2). Esta ecuación es esencialmente obvia a partir de la Figura 2.1, pero es una de esas cosas obvias peculiares que a menudo es difícil de ver. Una forma alternativa, que en ocasiones es más transparente, viene de tomar el complemento de ambos lados de (2.2), consiguiendo

\[\left\{S_{n}>t\right\}=\{N(t)<n\}\label{2.3} \]

Por ejemplo, el evento\(\left\{S_{1}>t\right\}\) significa que la primera llegada ocurre después\(t\), lo que significa\(\{N(t)<1\}\) (es decir,\(\{N(t)=0\}\)). Estas relaciones se usarán constantemente para ir y venir entre épocas de llegada y contar rv. En principio,\ ref {2.2} o\ ref {2.3} se pueden usar para especificar funciones de distribución conjunta de épocas de llegada en términos de funciones de distribución conjunta de variables de conteo y viceversa, así que ya sea caracterización se puede utilizar para especificar un proceso de llegada.

En resumen, entonces, un proceso de llegada puede ser especificado por las distribuciones conjuntas de las épocas de llegada, los intervalos entre llegadas, o los rv de conteo. En principio, especificando cualquiera de estos especifica también los otros. ³

---

Referencia

¹ Estas autocaravanas se\(S_{i}\) pueden ver como sumas de tiempos interllegados. No deben confundirse con los rv\(S_{i}\) utilizados en la Sección 1.3.5 para denotar el número de llegadas por tiempo\(i\) para el proceso Bernoulli. Usamos a\(S_{i}\) lo largo para denotar la suma de\(i\) rv. Comprender cómo se comportan tales sumas es un tema central de cada capítulo (y casi todas las secciones) de estas notas. Desafortunadamente, para el caso Bernoulli, las sumas IID de interés primario son las sumas de rv binarias en cada incremento de tiempo, mientras que aquí las sumas de interés primario son las sumas de los intervalos entre llegadas.

² Así, para el proceso de Bernoulli con un tamaño de incremento de 1,\(N(n)\) se denota la rv como\(S_{n}\) en la Sección 1.3.5

³ Por definición, un proceso estocástico es una colección de rv, por lo que uno podría preguntarse si un proceso de llegada (como proceso estocástico) es 'realmente' el proceso de la época de llegada\(0 \leq S_{1} \leq S_{2} \leq \cdots\) o el proceso de interllegada\(X_{1}, X_{2}, \ldots\) o el proceso de conteo\(\{N(t) ; t>0\}\). El proceso de tiempo de llegada se relaciona con las llegadas reales, el proceso interarrival suele ser el más simple, y el proceso de conteo 'se parece' más a un proceso estocástico en el tiempo ya que\(N(t)\) es un rv para cada uno\(t \geq 0\). Parece preferible, ya que las descripciones son tan claramente equivalentes, ver los procesos de llegada en términos de la descripción que sea más conveniente.