2.3: Combinar y dividir procesos de Poisson
- Page ID
- 86191
Supongamos que;:\(t>0\}\) y\(\left\{N_{2}(t) ; t>0\right\}\) son independientes los procesos de conteo de Poisson 8 de tasas\(\lambda_{1}\) y\(\lambda_{2}\) respectivamente. Queremos ver el proceso de suma donde\(N(t)=N_{1}(t)+N_{2}(t)\) para todos\(t \geq 0\). En otras palabras,\(\{N(t) ; t>0\}\) es el proceso que consiste en todas las llegadas tanto al proceso 1 como al proceso 2. Demostraremos que\(\{N(t) ; t>0\}\) es un proceso de conteo de Poisson de tasa\(\lambda=\lambda_{1}+\lambda_{2}\). Esto lo mostramos de tres maneras diferentes, primero usando la Definición 3 de un proceso de Poisson (ya que eso es lo más natural para este problema), luego usando la Definición 2, y finalmente la Definición 1. Luego sacamos algunas conclusiones sobre la manera en que cada enfoque es útil. Dado que\(\left\{N_{1}(t) ; t>0\right\}\) y\(\left\{N_{2}(t) ; t>0\right\}\) son independientes y cada uno posee las propiedades de incremento estacionario e independiente, se desprende de las definiciones que\(\{N(t) ; t>0\}\) también posee las propiedades de incremento estacionario e independiente. Usando las aproximaciones en\ ref {2.18} para los procesos individuales, vemos que
\ (\ begin {alineado}
\ nombreoperador {Pr}\ {\ tilde {N} (t, t+\ delta) =0\}\} &=\ nombreoperador {Pr}\ left\ {\ tilde {N} _ {1} (t, t+\ delta) =0\ derecho\}\ nombreoperador {Pr}\ izquierda\ {\ tilde {N} _ {2} (t, t+\ delta) =0\ derecha\}\\
&=\ izquierda (1-\ lambda_ {1}\ delta\ derecha)\ izquierda (1-\ lambda_ {2}\ delta\ derecha)\ aprox 1-\ lambda\ delta
\ final {alineado}\)
donde se\(\lambda_{1} \lambda_{2} \delta^{2}\) ha caído. De la misma manera,\(\operatorname{Pr}\{\tilde{N}(t, t+\delta)=1\}^\}\) se aproxima por\(\lambda \delta\) y\(\operatorname{Pr}\{\widetilde{N}(t, t+\delta) \geq 2\}^\}\) se aproxima por 0, ambos con errores proporcionales a\(\delta^{2}\). De ello se deduce que\(\{N(t) ; t>0\}\) es un proceso de Poisson.
En el segundo enfoque, tenemos\(N(t)=N_{1}(t)+N_{2}(t)\). Ya que\(N(t)\), para cualquier dado\(t\), es la suma de dos rv independientes de Poisson, también es un rv de Poisson con media\(\lambda t=\lambda_{1} t+\lambda_{2} t\). Si el lector no es consciente de que la suma de dos rv de Poisson independientes es Poisson, se puede derivar por convolución discreta de los dos PMF (ver Ejercicio 1.19). De manera más elegante, se puede observar que ya hemos mostrado implícitamente este hecho. Es decir, si rompemos un intervalo\(I\) en subintervalos disjuntos,\(I_{1}\) y\(I_{2}\), entonces el número de llegadas en\(I\) (que es Poisson) es la suma del número de llegadas en\(I_{1}\) y en\(I_{2}\) (que son independientes Poisson).
Por último, dado que\(N(t)\) es Poisson para cada uno\(t\), y dado que se satisfacen las propiedades de incremento estacionario e independiente,\(\{N(t) ; t>0\}\) es un proceso de Poisson.
En el tercer enfoque,\(X_{1}\), el primer intervalo entre llegadas para el proceso de suma, es el mínimo de\(X_{11}\), el primer intervalo entre llegadas para el primer proceso, y\(X_{21}\), el primer intervalo entre llegadas para el segundo proceso. Así\(X_{1}>t\), si y sólo si ambos\(X_{11}\) y\(X_{21}\) exceden\(t\), así
\(\operatorname{Pr}\left\{X_{1}>t\right\}=\operatorname{Pr}\left\{X_{11}>t\right\} \operatorname{Pr}\left\{X_{21}>t\right\}=\exp \left(-\lambda_{1} t-\lambda_{2} t\right)=\exp (-\lambda t)\)
Usando la propiedad sin memoria, cada intervalo posterior entre llegadas se puede analizar de la misma manera.
El primer enfoque anterior fue el más intuitivo para este problema, pero requirió un cuidado constante sobre el orden de magnitud de los términos que se descuidaban. El segundo enfoque fue el más simple analíticamente (después de reconocer que las sumas de rv de Poisson independientes son Poisson), y no requirió aproximaciones. El tercer enfoque fue muy sencillo en retrospectiva, pero no muy natural para este problema. Si sumamos muchos procesos independientes de Poisson, es claro, al agregarlos uno a la vez, que el proceso de suma vuelve a ser Poisson. Lo que es más interesante es que cuando se suman muchos procesos de conteo independientes (no necesariamente Poisson), el proceso de suma suele ser aproximadamente de Poisson si los procesos individuales tienen tasas pequeñas en comparación con la suma. Para obtener una intuición cruda sobre por qué esto podría esperarse, tenga en cuenta que los intervalos entre llegadas para cada proceso (suponiendo que no hay llegadas masivas) tenderán a ser grandes en relación con el intervalo medio entre llegadas para el proceso de suma. Por lo tanto, las llegadas que están muy juntas en el tiempo generalmente vendrán de diferentes procesos. El número de llegadas en un intervalo grande relativo al intervalo interllegada medio combinado, pero pequeño en relación con los intervalos individuales entre llegadas, será la suma del número de llegadas de los diferentes procesos; cada uno de estos es 0 con gran probabilidad y 1 con probabilidad pequeña, por lo que la suma será aproximadamente Poisson.
Subdivisión de un proceso de Poisson
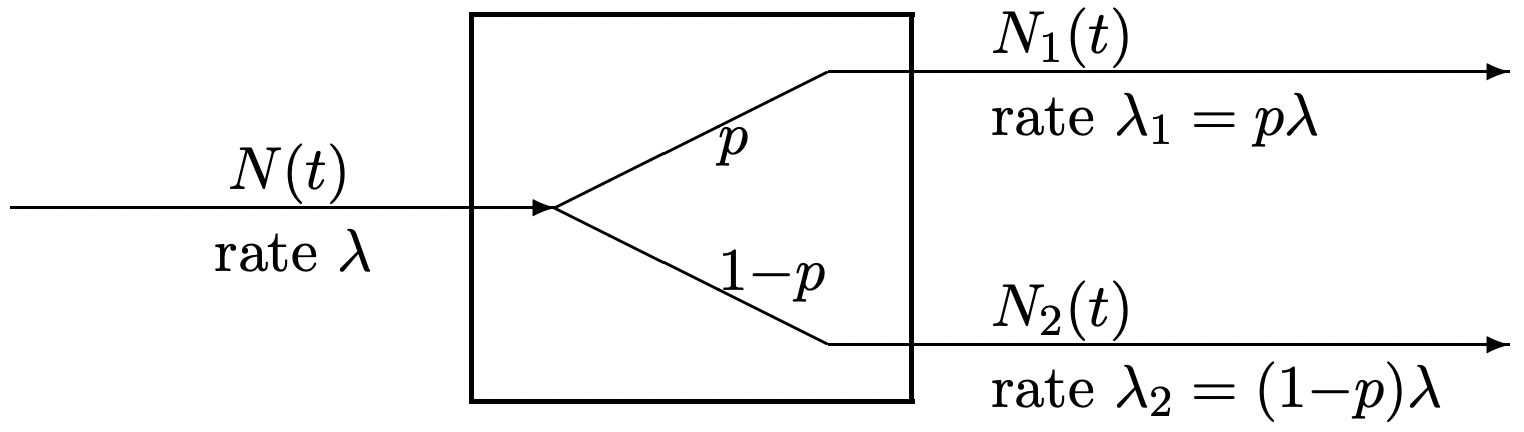
A continuación nos fijamos en cómo romper\(\{N(t) ; t>0\}\), un proceso de conteo de Poisson de tasa\(\lambda\), en dos procesos,\(\left\{N_{1}(t) ; t>0\right\}\) y\(\left\{N_{2}(t) ; t>0\right\}\). Supongamos que cada llegada\(\{N(t) ; t>0\}\) es enviada al primer proceso con probabilidad\(p\) y al segundo proceso con probabilidad\(1-p\) (ver Figura 2.6). Cada llegada se cambia independientemente de cada llegada e independientemente de las épocas de llegada. Puede ser útil visualizar esto como la combinación de dos procesos independientes. El primero es el proceso de Poisson de tasa\(\lambda\) y el segundo es un proceso de Bernoulli\(\left.X_{n} ; n \geq 1\right\}\) donde\(\mathrm{p}_{X_{n}}(1)=p\) y\(\mathrm{p}_{X_{n}}(2)=1-p\). La\(n\) llegada del proceso de Poisson se etiqueta entonces como una llegada de tipo 1 si\(X_{n}=1\) y como una llegada de tipo 2 con probabilidad\(1-p\).
Demostraremos que los procesos resultantes son cada uno de Poisson, con tasas\(\lambda_{1}=\lambda p\) y\(\lambda_{2}=\lambda(1-p)\) respectivamente, y que además los dos procesos son independientes. Obsérvese que, condicionados al proceso original, los dos nuevos procesos no son independientes; de hecho uno determina completamente al otro. Así esta independencia podría ser un poco sorprendente.
Primero considere un pequeño incremento\((t, t+\delta]\). El proceso original tiene una llegada a este intervalo incremental con probabilidad\(\lambda \delta\) (ignorando\(\delta^{2}\) términos como de costumbre), y así proceso 1
tiene una llegada con probabilidad p y proceso 2 con probabilidad\(\lambda \delta(1-p)\). Debido a la propiedad de incremento independiente del proceso original y la independencia de la división de cada llegada entre los dos procesos, los nuevos procesos tienen cada uno la propiedad de incremento independiente, y desde arriba tienen la propiedad de incremento estacionario. Así cada proceso es Poisson. Observe ahora que no podemos verificar que los dos procesos sean independientes de este modelo de pequeño incremento. Tendríamos que demostrar que el número de llegadas para el proceso 1 y 2 son independientes sobre\((t, t+\delta]\). Desafortunadamente, dejando fuera los términos de orden\(\delta^{2}\), hay como máximo una llegada al proceso original y no hay posibilidad de una llegada a cada nuevo proceso en\((t, t+\delta]\). Si es imposible que ambos procesos tengan una llegada en el mismo intervalo, no pueden ser independientes. Es posible, por supuesto, que cada proceso tenga una llegada en el mismo intervalo, pero este es un término de orden\(\delta^{2}\). Así, sin prestar atención a los términos del orden\(\delta^{2}\), es imposible demostrar que los procesos son independientes.
Para demostrar que los procesos 1 y 2 son independientes, primero calculamos el PMF conjunto para\(N_{1}(t)\),\(N_{2}(t)\) para arbitrario\(t\). Acondicionamiento en un número determinado de llegadas\(N(t)\) para el proceso original, tenemos
\[\operatorname{Pr}\left\{N_{1}(t)=m, N_{2}(t)=k \mid N(t)=m+k\right\}=\frac{(m+k) !}{m ! k !} p^{m}(1-p)^{k}\label{2.25} \]
La ecuación\ ref {2.25} es simplemente la distribución binomial, ya que, dadas las\(m+k\) llegadas al proceso original, cada una va independientemente al proceso 1 con probabilidad\(p\). Dado que el evento\(\left\{N_{1}(t)=m, N_{2}(t)=k\right\}\) es un subconjunto del evento condicionamiento anterior,
\(\operatorname{Pr}\left\{N_{1}(t)=m, N_{2}(t)=k \mid N(t)=m+k\right\}=\frac{\operatorname{Pr}\left\{N_{1}(t)=m, N_{2}(t)=k\right\}}{\operatorname{Pr}\{N(t)=m+k\}}\)
Combinando esto con (2.25), tenemos
\[\operatorname{Pr}\left\{N_{1}(t)=m, N_{2}(t)=k\right\}=\frac{(m+k !)}{m ! k !} p^{m}(1-p)^{k} \frac{(\lambda t)^{m+k} e^{-\lambda t}}{(m+k) !}\label{2.26} \]
Reordenando términos, obtenemos
\[\operatorname{Pr}\left\{N_{1}(t)=m, N_{2}(t)=k\right\}=\frac{(p \lambda t)^{m} e^{-\lambda p t}}{m !} \frac{[(1-p) \lambda t]^{k} e^{-\lambda(1-p) t}}{k !}\label{2.27} \]
Esto demuestra eso\(N_{1}(t)\) y\(N_{2}(t)\) son independientes. Para demostrar que los procesos son independientes, debemos demostrar que para cualquier\(k>1\) y cualquier conjunto de tiempos\(0 \leq t_{1} \leq t_{2} \leq \cdots \leq t_{k}\), los conjuntos\(\left\{N_{1}\left(t_{i}\right) ; 1 \leq i \leq k\right\}\) y\(\left\{N_{2}\left(t_{j}\right) ; 1 \leq j \leq k\right\}\) son independientes entre sí. Es equivalente a mostrar que los conjuntos\(\left\{\tilde{N}_{1}\left(t_{i-1}, t_{i}\right) ; 1 \leq i \leq k\right\}\) y\(\left\{\tilde{N}_{2}\left(t_{j-1}, t_{j}\right) ; 1 \leq j \leq k\right\}\) (donde\(t_{0}\) es 0) son independientes. El argumento anterior muestra esta independencia para\(i=j\), y para\(i \neq j\), la independencia se deriva del incremento independiente propiedad de\(\{N(t) ; t>0\}\).
Ejemplos usando procesos independientes de Poisson
Hemos observado que si las llegadas de un proceso de Poisson se dividen en dos nuevos procesos de llegada, cada llegada del proceso original entra independientemente en el primero de los nuevos procesos con cierta probabilidad fija\(p\), entonces los nuevos procesos son procesos de Poisson y son independientes. La consecuencia más útil de esto es que dos procesos de Poisson independientes pueden verse como generados a partir de un solo proceso de esta manera. Así, si un proceso tiene tasa\(\lambda_{1}\) y el otro tiene tasa\(\lambda_{2}\), pueden verse como provenientes de un proceso de tasa\(\lambda_{1}+\lambda_{2}\). Cada llegada al proceso combinado se etiqueta entonces como una primera llegada de proceso con probabilidad\(p=\lambda_{1} /\left(\lambda_{1}+\lambda_{2}\right)\) y como una segunda llegada de proceso con probabilidad\(1-p\).
El punto de vista anterior es muy útil para encontrar probabilidades como\(\operatorname{Pr}\left\{S_{1 k}<S_{2 j}\right\}\) dónde\(S_{1 k}\) está la época de la\(k\) llegada al primer proceso y\(S_{2 j}\) es la época de la\(j\) th llegada al segundo proceso. El problema se puede reformular en términos de un proceso combinado para preguntar: de las primeras\(k+j-1\) llegadas al proceso combinado, ¿cuál es la probabilidad de que\(k\) o más de ellos se cambien al primer proceso? (Obsérvese que si\(k\) o más de los primeros\(k+j-1\) van al primer proceso, a lo sumo\(j-1\) van al segundo, por lo que la\(k\) llegada a la primera precede a la\(j\) th llegada al segundo; de manera similar si menos\(k\) de los primeros\(k+j-1\) van al primer proceso, entonces el \(j\)th llegada al segundo proceso precede a la\(k\) th llegada al primero). Dado que cada una de estas primeras\(k+j-1\) llegadas se cambia independientemente con la misma probabilidad\(p\), la respuesta es
\[\operatorname{Pr}\left\{S_{1 k}<S_{2 j}\right\}=\sum_{i=k}^{k+j-1} \frac{(k+j-1) !}{i !(k+j-1-i) !} p^{i}(1-p)^{k+j-1-i}\label{2.28} \]
[La cola M/M/1] Los teóricos de la cola utilizan una notación estándar de caracteres separados por barra para describir tipos comunes de sistemas de colas. El primer personaje describe el proceso de llegada a la cola. \(M\)significa sin memoria y significa un proceso de llegada de Poisson;\(D\) significa determinista y significa que el intervalo entre llegadas es fijo y no aleatorio;\(G\) significa distribución general entre llegadas. Suponemos que los intervalos entre llegadas son IID (haciendo del proceso de llegada un proceso de renovación), pero muchos autores utilizan\(\text { GI }\) para indicar explícitamente las interllegadas IID. El segundo carácter describe el proceso de servicio. Se utilizan las mismas letras, con M indicando una distribución exponencial del tiempo de servicio. El tercer carácter da el número de servidores. Se supone, cuando se utiliza esta notación, que los tiempos de servicio son IID, independientes de los tiempos de llegada, e independientes de qué servidor se utiliza.
Solución
Considere una cola M/M/1, es decir, un sistema de colas con un sistema de llegada de Poisson (digamos de tarifa\(\lambda\)) y un solo servidor que atiende a los clientes que llegan en orden con una distribución del tiempo de servicio\(\mathrm{F}(y)=1-\exp [-\mu y]\). Así, durante los periodos en que el servidor está ocupado, los clientes abandonan el sistema de acuerdo a un proceso de Poisson (proceso 2) de tasa\(\mu\). Entonces vemos que si\(j\) o más clientes están esperando en un momento dado, entonces\ ref {2.28} da la probabilidad de que la késima llegada posterior venga antes de la salida\(j\) th.
Referencia
8 Dos procesos\(\left\{N_{1}(t) ; t>0\right\}\) y\(\left\{N_{2}(t) ; t>0\right\}\) se dice que son independientes si para todos los enteros positivos\(k\) y todos los conjuntos de tiempos\(0<t_{1}<t_{2}<\cdots<t_{k}\), las variables aleatorias\(N_{1}\left(t_{1}\right), \ldots, N_{1}\left(t_{k}\right)\) son independientes de\(N_{2}\left(t_{1}\right), \ldots, N_{2}\left(t_{k}\right)\). Aquí es suficiente extender la propiedad de incremento independiente a la independencia entre incrementos sobre los dos procesos; equivalentemente, uno puede requerir los intervalos entre llegadas para que un proceso sea independiente de las llegadas internas para el otro proceso.


