3.1: Introducción a las cadenas de Markov de estado finito
- Page ID
- 86166
Los procesos de conteo\(\{N(t) ; t>0\}\) descritos en la Sección 2.1.1 tienen la propiedad que\(N(t)\) cambia en instantes discretos de tiempo, pero se define para todos los reales\(t>0\). Las cadenas de Markov que se discutirán en este capítulo son procesos estocásticos definidos solo a valores enteros del tiempo,\(n=0,1, \ldots\). En cada tiempo entero\(n \geq 0\), hay una variable aleatoria de valor entero (rv)\(X_{n}\), llamada el estado en el tiempo\(n\), y el proceso es la familia de rv\(\left\{X_{n} ; n \geq 0\right\}\). Nos referimos a estos procesos como procesos de tiempo entero. Un proceso de tiempo entero también se\(\left\{X_{n} ; n \geq 0\right\}\) puede ver como un proceso\(\{X(t) ; t \geq 0\}\) definido para todos los reales\(t\) tomando\(X(t)=X_{n}\) para\(n \leq t<n+1\), pero dado que los cambios ocurren solo en tiempos enteros, generalmente es más sencillo ver el proceso solo en esos tiempos enteros.
En general, para las cadenas de Markov, el conjunto de valores posibles para cada rv\(X_{n}\) es un conjunto contable\(\mathcal{S}\). Si\(\mathcal{S}\) es contablemente infinito, generalmente se toma como ser\(\mathcal{S}=\{0,1,2, \ldots\}\), mientras que si\(\mathcal{S}\) es finito, generalmente se toma como ser\(\mathcal{S}=\{1, \ldots, \mathrm{M}\}\). En este capítulo (a excepción de los Teoremas 3.2.2 y 3.2.3), restringimos la atención al caso en el que\(\mathcal{S}\) es finito, es decir, procesos cuyas funciones de muestra son secuencias de enteros, cada una entre 1 y M. No hay un significado especial para usar etiquetas enteras para estados, y no hay razón convincente para incluir 0 para el caso contablemente infinito y no para el caso finito. Para el caso contablemente infinito, las aplicaciones más comunes provienen de la teoría de colas, donde el estado a menudo representa el número de clientes en espera, que podría ser cero. Para el caso finito, a menudo usamos vectores y matrices, donde las etiquetas enteras positivas simplifican la notación. En algunos ejemplos, será más conveniente usar etiquetas más ilustrativas para estados.
Una cadena de Markov es un proceso de tiempo entero,\(\left\{X_{n}, n \geq 0\right\}\) para el cual los valores de muestra para cada rv\(X_{n}\)\(n \geq 1\), se encuentran en un conjunto contable\(\mathcal{S}\) y dependen del pasado solo a través de la rv más reciente\(X_{n-1}\). Más específicamente, para todos los enteros positivos\(n\), y para todos\(i, j, k, \ldots, m\) en\(\mathcal{S}\),
\[\operatorname{Pr}\left\{X_{n}=j \mid X_{n-1}=i, X_{n-2}=k, \ldots, X_{0}=m\right\}=\operatorname{Pr}\left\{X_{n}=j \mid X_{n-1}=i\right\}\label{3.1} \]
Además,\(\operatorname{Pr}\left\{X_{n}=j \mid X_{n-1}=i\right\}\) depende solo de\(i\) y j (no\(n\)) y se denota por
\[\operatorname{Pr}\left\{X_{n}=j \mid X_{n-1}=i\right\}=P_{i j}\label{3.2} \]
El estado inicial\(X_{0}\) tiene una distribución de probabilidad arbitraria. Una cadena de Markov de estado finito es una cadena de Markov en la que\(\mathcal{S}\) es finita.
Ecuaciones como\ ref {3.1} suelen ser más fáciles de leer si se abrevian como
\(\operatorname{Pr}\left\{X_{n} \mid X_{n-1}, X_{n-2}, \ldots, X_{0}\right\}=\operatorname{Pr}\left\{X_{n} \mid X_{n-1}\right\}\)
Esta abreviatura significa que la igualdad se mantiene para todos los valores de muestra de cada una de las rv. Es decir, significa lo mismo que (3.1).
El rv\(X_{n}\) se llama el estado de la cadena en el momento\(n\). Los valores posibles para el estado en el momento\(n\), es decir\(\{1, \ldots, \mathrm{M}\}\) o\(\{0,1, \ldots\}\) también se denominan generalmente estados, generalmente sin demasiada confusión. Así\(P_{i j}\) es la probabilidad de ir a estado\(j\) dado que el estado anterior es\(i\); el nuevo estado, dado el estado anterior, es independiente de todos los estados anteriores. El uso de la palabra estado aquí se ajusta a la idea habitual del estado de un sistema —el estado en un momento dado resume todo lo relacionado con el pasado que es relevante para el futuro.
La definición 3.1.1 es utilizada por algunas personas como definición de una cadena homogénea de Markov. Para ellos, las cadenas de Markov incluyen casos más generales donde las probabilidades de transición pueden variar con n. Así reemplazan\ ref {3.1} y\ ref {3.2} por
\[\operatorname{Pr}\left\{X_{n}=j \mid X_{n-1}=i, X_{n-2}=k, \ldots, X_{0}=m\right\}=\operatorname{Pr}\left\{X_{n}=j \mid X_{n-1}=i\right\}=P_{i j}(n)\label{3.3} \]
Llamaremos a un proceso que obedece (3.3), con una dependencia de n, una cadena de Markov no homogénea. Discutiremos solo el caso homogéneo, sin dependencia de n, y así restringiremos la definición a ese caso. No se puede decir mucho de interés general sobre las cadenas no homogéneas. 1
Una distribución inicial de probabilidad para\(X_{0}\), combinada con las probabilidades de transición\(\left\{P_{i j}\right\}\) (o\(\left\{P_{i j}(n)\right\}\)) para el caso no homogéneo), define las probabilidades para todos los eventos en la cadena de Markov.
Las cadenas de Markov se pueden utilizar para modelar una enorme variedad de fenómenos físicos y pueden ser utilizadas para aproximarse a muchos otros tipos de procesos estocásticos como el siguiente ejemplo:
Considere un proceso entero\(\left\{Z_{n} ; n \geq 0\right\}\) donde los rv\(Z_{n}\) son finitos con valor entero como en una cadena de Markov, pero cada uno\(Z_{n}\) depende probabilísticamente de los\(k\) rv anteriores,\(Z_{n-1}, Z_{n-2}, \ldots, Z_{n-k}\). En otras palabras, utilizando la notación abreviada,
\[\operatorname{Pr}\left\{Z_{n} \mid Z_{n-1}, Z_{n-2}, \ldots, Z_{0}\right\}=\operatorname{Pr}\left\{Z_{n} \mid Z_{n-1}, \ldots Z_{n-k}\right\}\label{3.4} \]
- Contestar
-
Ahora mostramos cómo ver la condición en el lado derecho de (3.4), es decir,\(\left(Z_{n-1}, Z_{n-2}, \ldots, Z_{n-k}\right)\) como el estado del proceso en el momento\(n-1\). Podemos reescribir\ ref {3.4} como
\(\operatorname{Pr}\left\{Z_{n}, Z_{n-1}, \ldots, Z_{n-k+1} \mid Z_{n-1}, \ldots, Z_{0}\right\}=\operatorname{Pr}\left\{Z_{n}, \ldots, Z_{n-k+1} \mid Z_{n-1}, \ldots Z_{n-k}\right\}\)
ya que, para cada lado de la ecuación, cualquier conjunto dado de valores para\(Z_{n-1}, \ldots, Z_{n-k+1}\) en el lado derecho del signo de acondicionamiento especifica esos valores en el lado izquierdo. Así, si definimos\(X_{n-1}=\left(Z_{n-1}, \ldots, Z_{n-k}\right)\) para cada uno\(n\), esto simplifica a
\(\operatorname{Pr}\left\{X_{n} \mid X_{n-1}, \ldots, X_{k-1}\right\}=\operatorname{Pr}\left\{X_{n} \mid X_{n-1}\right\}\)
Vemos que al expandir el espacio estatal para incluir k-tuplas de los rv\(Z_{n}\), hemos convertido la dependencia a lo largo del tiempo en una\(k\) dependencia unitaria a lo largo del tiempo, es decir, se define un proceso de Markov usando el espacio de estado expandido.
Tenga en cuenta que en esta nueva cadena de Markov, el estado inicial es\(X_{k-1}=\left(Z_{k-1}, \ldots, Z_{0}\right)\), por lo que uno podría querer cambiar el eje de tiempo para empezar\(X_{0}\).
Las cadenas de Markov a menudo se describen mediante una gráfica dirigida (ver Figura 3.1 a). En esta representación gráfica, hay un nodo para cada estado y un arco dirigido para cada probabilidad de transición distinta de cero. Si\(P_{i j}=0\), entonces\(j\) se omite el arco de nodo\(i\) a nodo, por lo que la diferencia entre probabilidades de transición cero y distintas de cero destaca claramente en la gráfica. La clasificación de estados, como se discute en la Sección 3.2, está determinada por el conjunto de transiciones con probabilidades distintas de cero, y así la representación gráfica es ideal para ese tema.
Una cadena de Markov de estado finito también se describe a menudo mediante una matriz\([P]\) (ver Figura 3.1 b). Si la cadena tiene M estados, entonces\([P]\) es una matriz M por M con elementos\(P_{i j}\). La representación matricial es ideal para estudiar cuestiones algebraicas y computacionales.
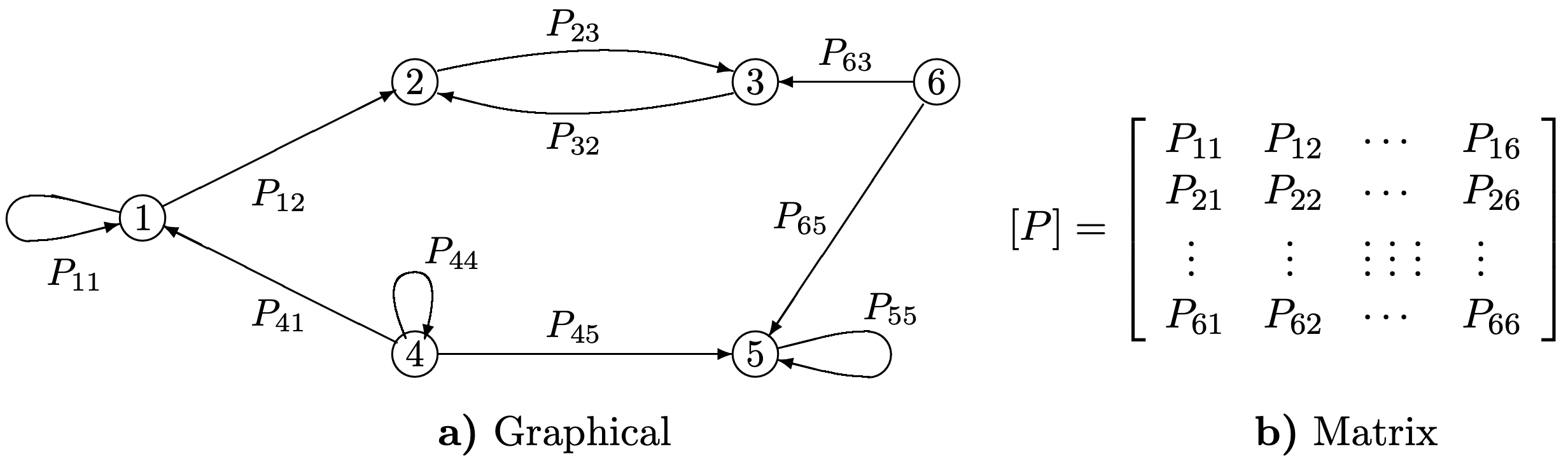
Figura 3.1: Representación Gráfica y Matriz de una Cadena Markov de 6 estados; un arco dirigido de\(i\) a\(j\) se incluye en la gráfica si y solo si (iff)\(P_{i j}>0\).
Referencia
1 Por otro lado, frecuentemente encontramos situaciones en las que un pequeño conjunto de rv, digamos\(W, X, Y, Z\) satisfacen la condición de Markov que\(\operatorname{Pr}\{Z \mid Y, X, W\}=\operatorname{Pr}\{Z \mid Y\}\) y\(\operatorname{Pr}\{Y \mid X, W\}=\operatorname{Pr}\{Y \mid X\}\) pero donde las distribuciones condicionales\(\operatorname{Pr}\{Z \mid Y\}\) y no\(\operatorname{Pr}\{Y \mid X\}\) están relacionadas. En otras palabras, las cadenas de Markov implican homogeneidad aquí, mientras que la condición de Markov no lo hace.


