3.3: La Representación Matrix

La matriz\([P]\) de probabilidades de transición de una cadena de Markov se denomina matriz estocástica; es decir, una matriz estocástica es una matriz cuadrada de términos no negativos en la que los elementos de cada fila suman a 1. Primero consideramos las probabilidades de transición de n pasos\(P_{i j}^{n}\) en términos de\(\text { [P] }\). La probabilidad, comenzando en estado\(i\), de ir a estado\(j\) en dos pasos es la suma sobre\(k\) de la probabilidad de ir primero a\(k\) y luego a\(j\). Usando la condición de Markov en (3.1),

\[P_{i j}^{2}=\sum_{k=1}^{M} P_{i k} P_{k j} \nonumber \]

Se puede ver que este es solo el\(ij\) término del producto de la matriz\([P]\) consigo mismo; denotando\([P][P]\) como\(\left[P^{2}\right]\), esto quiere decir que\(P_{i j}^{2}\) es el\((i, j)\) elemento de la matriz\(\left[P^{2}\right]\). De igual manera,\(P_{i j}^{n}\) es el\(i j\) elemento de la enésima potencia de la matriz\([P]\). Ya que\(\left[P^{m+n}\right]=\left[P^{m}\right]\left[P^{n}\right]\), esto significa que

\[P_{i j}^{m+n}=\sum_{k=1}^{\mathrm{M}} P_{i k}^{m} P_{k j}^{n}\label{3.8} \]

Esto se conoce como la ecuación de Chapman-Kolmogorov. Un enfoque eficiente para calcular\(\left[P^{n}\right]\) (y por lo tanto\(P_{i j}^{n}\)) para grandes\(n\), es multiplicar\([P]^{2}\) por\([P]^{2}\), luego\([P]^{4}\) por\([P]^{4}\) y así sucesivamente. Entonces se\([P],\left[P^{2}\right],\left[P^{4}\right], \ldots\) puede multiplicar según sea necesario para obtener\(\left[P^{n}\right]\).

Estado estacionario y [P ⁿ] para n grande

La matriz\(\left[P^{n}\right]\) (es decir, la matriz de probabilidades de transición elevadas a la potencia\(n\) th) es importante por varias razones. El\(i\),\(j\) elemento de esta matriz es\(P_{i j}^{n}=\operatorname{Pr}\left\{X_{n}=j \mid X_{0}=i\right\}\). Si la memoria del pasado se extingue con el aumento\(n\), entonces esperaríamos la\(P_{i j}^{n}\) dependencia de ambos\(n\) y\(i\) que desaparecieran como\(n \rightarrow \infty\). Esto significa, primero, que\(\left[P^{n}\right]\) debe converger a un límite como\(n \rightarrow \infty\), y, segundo, que para cada columna\(j\), los elementos en esa columna,\(P_{1 j}^{n}, P_{2 j}^{n}, \ldots, P_{\mathrm{M} j}^{n}\) deberían tender todos hacia el mismo valor, digamos\(\pi j\), como\(n \rightarrow \infty\). Si se produce este tipo de convergencia, (y posteriormente determinamos las circunstancias bajo las cuales ocurre), entonces\(P_{i j}^{n} \rightarrow \pi_{j}\) y cada fila de la matriz limitante será\(\left(\pi_{1}, \ldots, \pi_{\mathrm{M}}\right)\), es decir, cada fila es la misma que la otra fila.

Si ahora miramos la ecuación\(P_{i j}^{n+1}=\sum_{k} P_{i k}^{n} P_{k j}\), y asumimos el tipo de convergencia anterior como\(n \rightarrow \infty\), entonces la ecuación limitante se convierte\(\pi_{j}=\sum \pi_{k} P_{k j}\). En forma vectorial, esta ecuación es\(\boldsymbol{\pi}=\boldsymbol{\pi}[P]\). Esto lo haremos con más cuidado después, pero lo que dice es que si se\(P_{i j}^{n}\) acerca a un límite denotado\(\pi j\) como\(n \rightarrow \infty\), entonces\(\boldsymbol{\pi}=\left(\pi_{1}, \ldots, \pi_{\mathrm{M}}\right)\) satisface\(\boldsymbol{\pi}=\boldsymbol{\pi}[P]\). Si nada más, es más fácil resolver las ecuaciones lineales\(\boldsymbol{\pi}=\boldsymbol{\pi}[P]\) que multiplicar\([P] \) por sí mismo un número infinito de veces.

Definición: 3.1.1

Un vector de estado estacionario (o una distribución de estado estacionario) para una cadena de Markov de\(M\) estado con matriz de transición\([P]\) es un vector de fila\(\boldsymbol{\pi}\) que satisface

\[\boldsymbol{\pi}=\boldsymbol{\pi}[P] ; \quad \text { where } \sum_{i} \pi_{i}=1 \text { and } \pi_{i} \geq 0,1 \leq i \leq M\label{3.9} \]

Si\(\boldsymbol{\pi}\) satisface (3.9), entonces la última mitad de la ecuación dice que debe ser un vector de probabilidad. Si\(\boldsymbol{\pi}\) se toma como el PMF inicial de la cadena en el tiempo 0, entonces ese PMF se mantiene para siempre. Es decir, post-multiplicar ambos lados de\ ref {3.9} por\([P]\), obtenemos\(\boldsymbol{\pi}[P]=\boldsymbol{\pi}\left[P^{2}\right]\), e iterando esto,\(\boldsymbol{\pi}=\boldsymbol{\pi}\left[P^{2}\right]=\boldsymbol{\pi}\left[P^{3}\right]=\cdots\) para todos\(n\).

Es importante reconocer que hemos demostrado que si\(\left[P^{n}\right]\) converge a una matriz todas cuyas filas son\(\boldsymbol{\pi}\), entonces\(\boldsymbol{\pi}\) es un vector de estado estacionario, es decir, satisface (3.9). Sin embargo, encontrar una\(\boldsymbol{\pi}\) que satisfaga\ ref {3.9} no implica que\(\left[P^{n}\right]\) converja como\(n \rightarrow \infty\). Para el ejemplo de la Figura 3.1, se puede observar que si elegimos\(\pi_{2}=\pi_{3}=1 / 2\) con\(\pi_{i}=0\) otra cosa, entonces\(\boldsymbol{\pi}\) es un vector de estado estacionario. Razonando más físicamente, vemos que si la cadena está en cualquiera de los estados 2 o 3, simplemente oscila entre esos estados para siempre. Si comienza en el tiempo 0 estando en estados 2 o 3 con igual probabilidad, entonces persiste para siempre estando en estados 2 o 3 con igual probabilidad. Si bien esta elección de\(\boldsymbol{\pi}\) satisface la definición en\ ref {3.9} y también es una distribución de estado estacionario en el sentido de no cambiar con el tiempo, no es una forma muy satisfactoria de estado estacionario, y casi parece estar ocultando el hecho de que estamos ante una simple oscilación entre estados.

Este ejemplo plantea una de una serie de preguntas que deben ser respondidas en relación con las distribuciones en estado estacionario y la convergencia de\(\left[P^{n}\right]\):

1. ¿Bajo qué condiciones\(\boldsymbol{\pi}=\boldsymbol{\pi}[P]\) tiene una solución de vector de probabilidad?
2. ¿Bajo qué condiciones\(\boldsymbol{\pi}=\boldsymbol{\pi}[P]\) tiene una solución de vector de probabilidad única?
3. ¿Bajo qué condiciones\(\left[P^{n}\right]\) converge cada fila de a una solución de vector de probabilidad de\(\boldsymbol{\pi}=\boldsymbol{\pi}[P]\)?

Primero damos las respuestas a estas preguntas para las cadenas de Markov de estado finito y luego las derivamos. Primero,\ ref {3.9} siempre tiene una solución (aunque esto no es necesariamente cierto para las cadenas infinitestate). Las respuestas a las preguntas segunda y tercera se simplifican si utilizamos la siguiente definición:

Definición 3.3.2

Una unicaína es una cadena de Markov de estado finito que contiene una sola clase recurrente más, quizás, algunos estados transitorios. Una unicaína ergódica es una unicaína para la cual la clase recurrente es ergódica.

Una unicaína, como veremos, es la generalización natural de una cadena recurrente para permitir algún comportamiento transitorio inicial sin perturbar el comportamiento aymptótico a largo plazo de la cadena recurrente subyacente.

La respuesta a la segunda pregunta anterior es que la solución a\ ref {3.9} es única si y solo si\([\mathrm{P}]\) es la matriz de transición de una unicadena. Si hay clases\(c\) recurrentes, entonces\ ref {3.9} tiene soluciones\(c\) linealmente independientes, cada una distinta de cero solo sobre los elementos de la clase recurrente correspondiente. Para la tercera pregunta, cada fila de\(\left[P^{n}\right]\) converge a la solución única de\ ref {3.9} si y solo si\([\mathrm{P}]\) es la matriz de transición de una unicadena ergódica. Si hay múltiples clases recurrentes, y cada una es aperiódica, entonces\(\left[P^{n}\right]\) todavía converge, pero a una matriz con filas no idénticas. Si la cadena de Markov tiene una o más clases periódicas recurrentes, entonces\(\left[P^{n}\right]\) no converge.

Primero miramos estas respuestas desde el punto de vista de las matrices de transición de las cadenas de Markov de estado finito, y luego procedemos en el Capítulo 5 a analizar el problema más general de las cadenas de Markov con un número contablemente infinito de estados. Allí utilizamos la teoría de la renovación para responder a estas mismas preguntas (y para descubrir las diferencias que ocurren para las cadenas de Markov de estado infinito).

El enfoque matricial es útil computacionalmente y también tiene la ventaja de decirnos algo sobre las tasas de convergencia. El enfoque que utiliza la teoría de la renovación es muy simple (dada una comprensión de los procesos de renovación), pero es más abstracto.

Al responder a las preguntas anteriores (más algunas más) para las cadenas de Markov de estado finito, es más sencillo considerar primero la tercera pregunta, ⁴ es decir, la convergencia de\(\left[P^{n}\right]\). El enfoque más simple para esto, para cada columna\(j\) de\(\left[P^{n}\right]\), es estudiar la diferencia entre el elemento más grande y el más pequeño de esa columna y cómo cambia esta diferencia con\(n\). El siguiente lema casi trivial inicia este estudio, y es válido para todas las cadenas de Markov de estado finito.

Lema 3.3.1

\([P]\)Sea la matriz de transición de una cadena de Markov de estado finito y deje\(\left[P^{n}\right]\) ser la enésima potencia de\([P]\) i.e., la matriz de probabilidades de transición de orden n,\(P_{i j}^{n}\). Luego para cada estado\(j\) y cada entero\(n \geq 1\)

\[\max _{i} P_{i j}^{n+1} \leq \max _{\ell} P_{\ell j}^{n} \quad \min _{i} P_{i j}^{n+1} \geq \min _{\ell} P_{\ell j}^{n}\label{3.10} \]

Discusión

El lema dice que para cada columna\(j\), el mayor de los elementos no aumenta con\(n\) y el más pequeño de los elementos no disminuye con\(n\). Los elementos de una columna que forman el máximo y mínimo pueden cambiar con\(n\), pero el rango cubierto por esos elementos se anida en\(n\), ya sea encogiéndose o permaneciendo igual que\(n \rightarrow \infty\).

Prueba

Para cada uno\(i, j, n\), utilizamos la ecuación de Chapman-Kolmogorov, (3.8), seguida del hecho de que\(P_{k j}^{n} \leq \max _{\ell} P_{\ell j}^{n}\), para ver que

\[P_{i j}^{n+1}=\sum_{k} P_{i k} P_{k j}^{n} \leq \sum_{k} P_{i k} \max _{\ell} P_{\ell j}^{n}=\max _{\ell} P_{\ell j}^{n}\label{3.11} \]

Dado que esto es válido para todos los estados\(i\), y por lo tanto para la maximización\(i\), sigue la primera mitad de\ ref {3.10}. La segunda mitad de\ ref {3.10} es la misma, con mínimos reemplazando máximos, es decir,

\[P_{i j}^{n+1}=\sum_{k} P_{i k} P_{k j}^{n} \geq \sum_{k} P_{i k} \min _{\ell} P_{\ell j}^{n}=\min _{\ell} P_{\ell j}^{n}\label{3.12} \]

Para algunas cadenas de Markov, los elementos maximizadores en cada columna disminuyen\(n\) y alcanzan un límite igual a la secuencia creciente de elementos minimizadores. Para estas cadenas,\(\left[P^{n}\right]\) converge a una matriz donde cada columna es constante, es decir, el tipo de convergencia discutido anteriormente. Para otros, los elementos maximizadores convergen en algún valor estrictamente por encima del límite de los elementos minimizadores, entonces\(\left[P^{n}\right]\) no converge a una matriz donde cada columna sea constante, y podría no converger en absoluto ya que la ubicación de los elementos maximizadores y minimizadores en cada columna puede variar con \(n\).

Las tres subsecciones siguientes establecen el tipo de convergencia anterior (y una serie de resultados subsidiarios) para tres casos de creciente complejidad. El primero asume eso\(P_{i j}>0\) para todos\(i, j\). Esto se denota como\([P]>0\) y no es de gran interés por derecho propio, sino que proporciona un paso necesario para los demás casos. El segundo caso es donde la cadena de Markov es ergódica, y el tercero es donde la cadena de Markov es una unicadena ergódica.

Suponiendo en estado estacionario [P] > 0

Lema 3.3.2

Deje que la matriz de transición de una cadena de Markov de estado finito satisfaga\([P]>0\) (es decir,\(P_{i j}>0\) para todos\(i, j\)), y deje\(\alpha=\min _{i, j} P_{i j}\). Entonces para todos los estados\(j\) y todos\(n \geq 1\):

\[\max _{i} P_{i j}^{n+1}-\min _{i} P_{i j}^{n+1} \leq\left(\max _{\ell} P_{\ell j}^{n}-\min _{\ell} P_{\ell j}^{n}\right)(1-2 \alpha)\label{3.13} \]

\[\left(\max _{\ell} P_{\ell j}^{n}-\min _{\ell} P_{\ell j}^{n}\right) \leq(1-2 \alpha)^{n}.\label{3.14} \]

\[\lim _{n \rightarrow \infty} \max _{\ell} P_{\ell j}^{n}=\lim _{n \rightarrow \infty} \min _{\ell} P_{\ell j}^{n}>0\label{3.15} \]

Discusión

Ya que\(P_{i j}>0\) para todos\(i, j\), debemos tener\(\alpha>0\). Así el teorema dice que para cada uno\(j\), los elementos\(P_{i j}^{n}\) en columna\(j\) de\(\left[P^{n}\right]\) aproximación a la igualdad sobre ambos\(i\) y\(n\) como\(n \rightarrow \infty\), es decir, el estado en el tiempo\(n\) se vuelve independiente del estado en el tiempo 0 as\(n \rightarrow \infty\). El enfoque es exponencial en\(n\).

Prueba

Primero apretamos ligeramente la desigualdad en (3.11). Para un dado\(j\) y\(n\), dejar\(\ell_{\min }\) ser un valor de\(\ell\) que minimice\(P_{\ell j}^{n}\). Entonces

\ (\ begin {alineado}
P_ {i j} ^ {n+1} &=\ suma_ {k} P_ {i k} P_ {k j} ^ {n}\\
&\ leq\ suma_ {k\ neq\ ell_ {\ min}} P_ {i k}\ max _ {\ ell} P_ {\ ell j} ^ {n} +P_ {i\ ell_ {\ min}}\ min _ {\ ell} P_ {\ ell j} ^ {n}\\
&=\ max _ {\ ell} P_ {\ ell j} ^ {n} -P_ {i\ ell_ {\ min}}\ left (\ max _ {\ ell} P_ {\ ell j} ^ {n} -\ min _ {\ ell} P_ {\ ell j} ^ {n}\ derecha)\\
&\ leq\ max _ {\ ell} P_ {\ ell j} ^ {n} -\ alfa\ izquierda (\ max _ {\ ell} P_ {\ ell} ^ {n} -\ min _ {\ ell} P_ {\ ell j} ^ {n}\ derecha),
\ fin {alineado}\)

donde en el tercer paso, sumamos y restamos\(P_{i \ell_{\min }} \min _{\ell} P_{\ell j}^{n}\) al lado derecho, y en el cuarto paso, usamos\(\alpha \leq P_{i \ell_{\min }}\) en conjunción con el hecho de que el término entre paréntesis debe ser no negativo.

Repitiendo el mismo argumento con los roles de max y min invertidos,

\(P_{i j}^{n+1} \geq \min _{\ell} P_{\ell j}^{n}+\alpha\left(\max _{\ell} P_{\ell j}^{n}-\min _{\ell} P_{\ell j}^{n}\right)\).

El límite superior anterior se aplica a\(\max _{i} P_{i j}^{n+1}\) y el límite inferior a\(\min _{i} P_{i j}^{n+1}\). Así, restando el límite inferior del límite superior, obtenemos (3.13).

Por último, tenga en cuenta que

\(\min _{\ell} P_{\ell j} \geq \alpha>0 \quad \max _{\ell} P_{\ell j} \leq 1-\alpha\)

Así\(\max _{\ell} P_{\ell j}-\min _{\ell} P_{\ell j} \leq 1-2 \alpha\). Usando esto como la base para iterar\ ref {3.13} over\(n\), obtenemos (3.14). Esto, en conjunción con (3.10), muestra no sólo que los límites en\ ref {3.10} existen y son positivos e iguales, sino que los límites se acercan exponencialmente en\(n\).

Cadenas ergódicas de Markov

Lema 3.3.2 se extiende con bastante facilidad a cadenas arbitrarias ergódicas de estado finito de Markov. La clave de esto viene del Teorema 3.2.4, que muestra que si\([P]\) es la matriz para una cadena de Markov ergódica\(M\) estatal, entonces la matriz\(\left[P^{h}\right]\) es positiva para cualquiera\(h \geq(\mathrm{M}-1)^{2}-1\). Así, eligiendo\(h=(\mathrm{M}-1)^{2}-1\), podemos aplicar Lema 3.3.2 a\(\left[P^{h}\right]>0\). Para cada número entero\(\nu \geq 1\),

\[ \max _{i} P_{i j}^{h(\nu+1)}-\min _{i} P_{i j}^{h(\nu+1)} \leq\left(\max _{m} P_{m j}^{h \nu}-\min _{m} P_{m j}^{h \nu}\right)(1-2 \beta)\label{3.16} \]

\ [\ begin {align}
\ left (\ max _ {m} P_ {m j} ^ {h\ nu} -\ min _ {m} P_ {m j} ^ {h\ nu}\ derecha) &\ leq (1-2\ beta) ^ {\ nu}\
\ lim _ {\ nu\ fila derecha\ infty}\ max _ {m} P_ {m j} ^ ^ h\ nu} &=\ lim _ {\ nu\ fila derecha\ infty}\ min _ {m} P_ {m j} ^ {h\ nu} >0,
\ end {align}\ label {3.17}\]

donde\(\beta=\min _{i, j} P_{i j}^{h}\). Lema 3.3.1 afirma que\(\max _{i} P_{i j}^{n+1}\) es no decreciente en\(n\), de manera que el límite de la izquierda en\ ref {3.17} puede ser reemplazado por un límite en\(n\). De igual manera, el límite de la derecha puede ser reemplazado por un límite on\(n\), consiguiendo

\[ \left(\max _{m} P_{m j}^{n}-\min _{m} P_{m j}^{n}\right) \leq(1-2 \beta)^{\lfloor n / h\rfloor}\label{3.18} \]

\[ \lim _{n \rightarrow \infty} \max _{m} P_{m j}^{n}=\lim _{n \rightarrow \infty} \min _{m} P_{m j}^{n}>0\label{3.19} \]

Ahora define\(\pi>0\) por

\[ \pi_{j}=\lim _{n \rightarrow \infty} \max _{m} P_{m j}^{n}=\lim _{n \rightarrow \infty} \min _{m} P_{m j}^{n}>0\label{3.20} \]

Dado que\(\pi_{j}\) se encuentra entre el mínimo y el máximo\(P_{i j}^{n}\) para cada uno\(n\),

\[ \left|P_{i j}^{n}-\pi_{j}\right| \leq(1-2 \beta)^{\lfloor n / h\rfloor}\label{3.21} \]

En el límite, entonces,

\[ \lim _{n \rightarrow \infty} P_{i j}^{n}=\pi_{j} \quad \text { for each } i, j\label{3.22} \]

Esto dice que la matriz\(\left[P^{n}\right]\) tiene un límite como\(n \rightarrow \infty\) y el\(i, j\) término de esa matriz es\(\pi_{j}\) para todos\(i, j\). En otras palabras, cada fila de esta matriz limitante es la misma y es el vector\(\boldsymbol{\pi}\). Esto está representado de manera más compacta por

\[ \lim _{n \rightarrow \infty}\left[P^{n}\right]=\boldsymbol{e} \pi \quad \text { where } \boldsymbol{e}=(1,1, \ldots, 1)^{\top}\label{3.23} \]

El siguiente teorema ⁵ resume estos resultados y agrega un pequeño resultado adicional.

Teorema 3.3.1

\([P]\)Sea la matriz de una cadena ergódica de Markov de estado finito. Luego hay\(a\) un vector de estado estacionario único\(\boldsymbol{\pi}\), ese vector es positivo y satisface\ ref {3.22} y (3.23). La convergencia en n es exponencial, satisfactoria (3.18).

Prueba

Necesitamos mostrar que\(\boldsymbol{\pi}\) como se define en\ ref {3.20} es el vector único de estado estacionario. Let\(\boldsymbol\mu\) Ser cualquier vector de estado estacionario, es decir, cualquier solución de vector de probabilidad a\(\boldsymbol{\mu}[P]=\boldsymbol\mu\). Entonces\(\boldsymbol\mu\) hay que satisfacer\(\boldsymbol{\mu}=\boldsymbol{\mu}\left[P^{n}\right]\) para todos\(n>1\). Yendo al límite,

\(\boldsymbol{\mu}=\boldsymbol{\mu} \lim _{n \rightarrow \infty}\left[P^{n}\right]=\boldsymbol{\mu} \boldsymbol{e} \boldsymbol{\pi}=\boldsymbol{\pi}\)

Así\(\boldsymbol{\pi}\) es un vector de estado estacionario y es único

Unichains Ergódicos

Comprender cómo\(P_{i j}^{n}\) se acerca a un límite como\(n \rightarrow \infty\) para las unicenas ergódicas es una extensión directa ij de los resultados en la Sección 3.3.3, pero los detalles requieren un poco de cuidado. Let\(\mathcal{T}\) denotar el conjunto de estados transitorios (que podrían contener varias clases transitorias), y

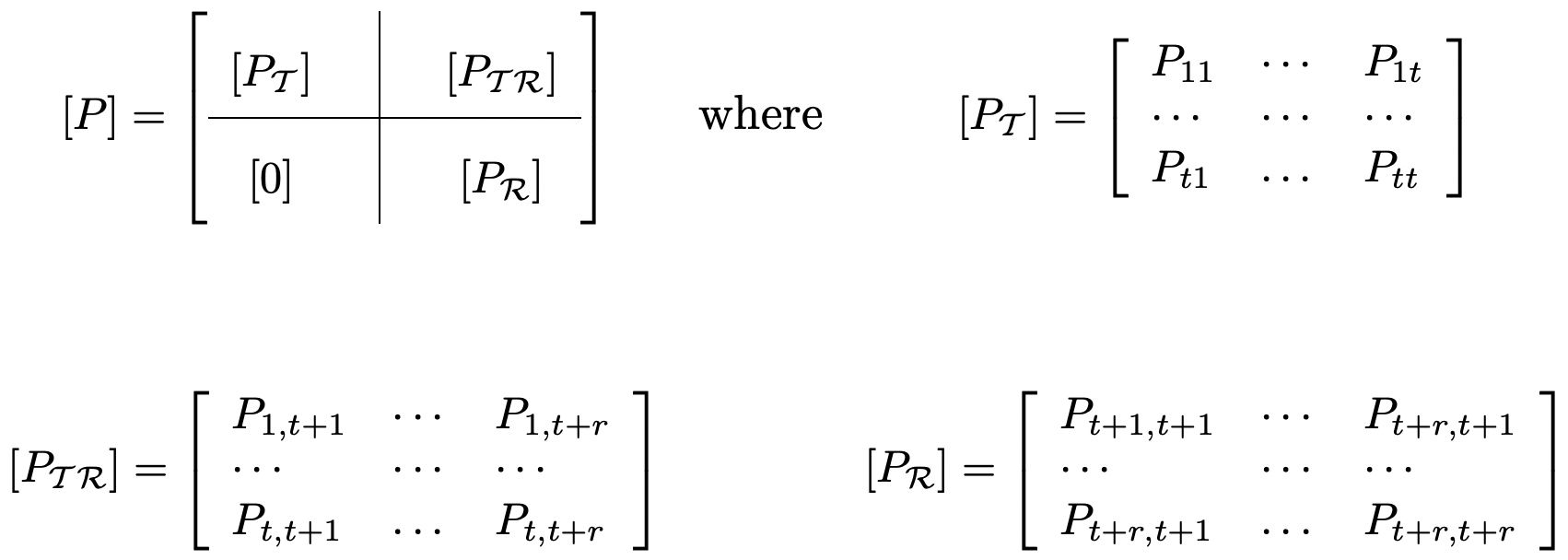Figura 3.5: La matriz de transición de una unicaína. El bloque de ceros en la parte inferior izquierda corresponde a la ausencia de transiciones de estados recurrentes a transitorios.

asumir los estados de\(\mathcal{T}\) están numerados 1, 2,.,\(t\). Dejar\(\mathcal{R}\) denotar la clase recurrente, que se supone que está numerada\(t+1, \ldots, t+r\) (ver Figura 3.5).

Si\(i\) y\(j\) son ambos estados recurrentes, entonces no hay posibilidad de salir de la clase recurrente al pasar de\(i\) a\(j\). Suponiendo que esta clase es ergódica, la matriz de transición\(\left[P_{\mathcal{R}}\right]\) como se muestra en la Figura 3.5 ha sido analizada en la Sección 3.3.3.

Si el estado inicial es un estado transitorio, entonces eventualmente se ingresa la clase recurrente, y eventualmente después de eso, la distribución se acerca al estado estacionario dentro de la clase recurrente. Esto sugiere (y a continuación mostramos) que hay un vector de estado estacionario\(\boldsymbol{\pi}\) para\([P]\) sí mismo tal que\(\pi_{j}=0\) para\(j \in \mathcal{T}\) y\(\pi j\) es como se da en la Sección 3.3.3 para cada uno\(j \in \mathcal{R}\).

Inicialmente vamos a mostrar que\(P_{i j}^{n}\) converge a 0 para\(i, j \in \mathcal{T}\). La naturaleza exacta de cómo e ij cuando se ingresa la clase recurrente comenzando en un estado transitorio es un problema interesante por derecho propio, y se discute más adelante. Por ahora, bastará con un crudo encuadernado.

Para cada estado transitorio, debe haber una caminata a algún estado recurrente, y dado que solo hay estados\(t\) transitorios, debe haber alguna trayectoria de este tipo de longitud como máximo\(t\). Cada uno de esos caminos tiene probabilidad positiva, y por lo tanto para cada uno\(i \in \mathcal{T}\),\(\sum_{j \in \mathcal{R}} P_{i j}^{t}>0\). De ello se deduce que para cada uno\(i \in \mathcal{T}\),\(\sum_{j \in \mathcal{T}} P_{i j}^{t}<1\). Dejar\(\gamma<1\) ser el máximo de estas probabilidades sobre\(i \in \mathcal{T}\), es decir,

\(\gamma=\max _{i \in \mathcal{T}} \sum_{j \in \mathcal{T}} P_{i j}^{t}<1\)

Teorema 3.3.3

Dejar\([P]\) ser una unichain con un conjunto\(\mathcal{T}\) de estados\(t\) transitorios. Entonces

\[\max _{\ell \in \mathcal{T}} \sum_{j \in \mathcal{T}} P_{\ell j}^{n} \leq \gamma^{\lfloor n / t\rfloor}\label{3.24} \]

Prueba

Para cada múltiplo entero\(\nu t\) y cada uno\(i \in \mathcal{T}\),

\(\sum_{j \in \mathcal{T}} P_{i j}^{(\nu+1) t}=\sum_{k \in \mathcal{T}} P_{i k}^{t} \sum_{j \in \mathcal{T}} P_{k j}^{\nu t} \leq \sum_{k \in \mathcal{T}} P_{i k}^{t} \max _{\ell \in \mathcal{T}} \sum_{j \in \mathcal{T}} P_{\ell j}^{\nu t} \leq \gamma \max _{\ell \in \mathcal{T}} \sum_{j \in \mathcal{T}} P_{\ell j}^{\nu t}\)

Reconociendo que esto se aplica a todos\(i \in \mathcal{T}\), y así al máximo sobre\(i\), podemos iterar esta ecuación, obteniendo

\(\max _{\ell \in \mathcal{T}} \sum_{j \in \mathcal{T}} P_{\ell j}^{\nu t} \leq \gamma^{\nu}\)

Dado que este máximo no aumenta en\(n\), sigue\ ref {3.24}.

Pasamos ahora al caso donde está el estado inicial\(i \in \mathcal{T}\) y el estado final está\(j \in \mathcal{R}\). Vamos\(m=\lfloor n / 2\rfloor\). Para cada uno\(i \in \mathcal{T}\) y\(j \in \mathcal{R}\), la ecuación Chapman-Kolmogorov, dice que

\(P_{i j}^{n}=\sum_{k \in \mathcal{T}} P_{i k}^{m} P_{k j}^{n-m}+\sum_{k \in \mathcal{R}} P_{i k}^{m} P_{k j}^{n-m}\)

\(\pi j\)Sea la probabilidad de estado estacionario\(j \in \mathcal{R}\) en la cadena recurrente de Markov con estados\(\mathcal{R}\), es decir,\(\pi_{j}=\lim _{n \rightarrow \infty} P_{k j}^{n}\). Entonces para cada uno\(i \in \mathcal{T}\),

\ (\ begin {alineado}
\ izquierda|p_ {i j} ^ {n} -\ pi_ {j}\ derecha| &=\ izquierda|\ sum_ {k\ in\ mathcal {T}} P_ {i k} ^ {m}\ izquierda (P_ {k j} ^ {n-m} -\ pi_ {j}\ derecha) +\ sum_ {k\ in\ mathcal {R}} P_ {i k} ^ {m}\ izquierda (P_ {k j} ^ {n-m} -\ pi_ {j}\ derecha)\ derecha|\\
&\ leq\ suma_ {k\ in\ mathcal {T}} P_ {i k} ^ {m}\ izquierda|P_ {k j} ^ {n-m} -\ pi_ {j}\ derecha|+\ sum_ {k\ in\ mathcal {R}} P_ {i k} ^ {m}\ izquierda|P_ {k j} ^ {n-m} -\ pi_ {j}\ derecha|\\
&\ leq\ suma_ {k\ in\ mathcal {T}} P_ {i k} ^ {m} +\ sum_ {k\ in\ mathcal {R}} P_ {i k} ^ {m}\ izquierda|P_ {k j} ^ {n-m} -\ pi_ {j}\ derecha|\ quad& (3.25)\\
&\ leq\ gamma^ {\ lpiso m/t\ rpiso} + (1 -2\ beta) ^ {\ lpiso (n-m)/h\ rpiso}, &\ quad (3.26)
\ final {alineado}\)

donde el primer escalón superior limitaba el valor absoluto de una suma por la suma de los valores absolutos. En el último paso, se utilizó\ ref {3.24} en la primera mitad de\ ref {3.25} y\ ref {3.21} (con\(h=(r-1)^{2}-1\) y\(\beta=\min _{i, j \in \mathcal{R}} P_{i j}^{h}>0\) se utilizó en la segunda mitad.

Esto se resume en el siguiente teorema.

Teorema 3.3.2

\([P]\)Sea la matriz de una unicaína ergódica de estado finito. Entonces\(\lim _{n \rightarrow \infty}\left[P^{n}\right]=\boldsymbol{e\pi}\) donde\(\boldsymbol{e}=(1,1, \ldots, 1)^{T}\) y\(\boldsymbol{\pi}\) es el vector de estado estacionario de la clase recurrente de estados, expandido en 0's para cada estado transitorio de la unicadena. La convergencia es exponencial en\(n\) para todos\(i\),\(j\).

Cadenas arbitrarias de Markov de estado finito

El comportamiento asintótico de las\(\left[P^{n}\right]\) cadenas arbitrarias de Markov en estado finito se puede deducir principalmente del caso de la unicadena ergódica mediante simples extensiones y sentido común.\(n \rightarrow \infty\)

Primero considere el caso de clases\(m>1\) aperiódicas más un conjunto de estados transitorios. Si el estado inicial está en el° de las clases recurrentes, digamos\(\mathcal{R}^{\kappa}\) entonces la cadena permanece en\(\mathcal{R}^{\kappa}\) y hay un vector único de estado finito\(\boldsymbol{\pi}^{\kappa}\) que es distinto de cero solo en\(\mathcal{R}^{\kappa}\) que se puede encontrar viendo la clase\(\kappa\) de forma aislada.

Si el estado inicial i es transitorio, entonces, para cada uno\(\mathcal{R}^{\kappa}\), existe una cierta probabilidad de que finalmente\(\mathcal{R}^{\kappa}\) se alcance, y una vez que se alcanza no hay salida, por lo que se aproxima al estado estacionario sobre esa clase recurrente. La cuestión de encontrar la probabilidad de ingresar a cada clase recurrente a partir de una clase transitoria dada se discutirá en la siguiente sección.

A continuación considere una cadena recurrente de Markov que sea periódica con periodo\(d\). La matriz de probabilidad de transición de orden\(d\) th\(\left[P^{d}\right]\),, se ve entonces restringida por el hecho de que\(P_{i j}^{d}=0\) para todos\(j\) no en el mismo subconjunto periódico que\(i\). En otras palabras,\(\left[P^{d}\right]\) es la matriz de una cadena con clases\(d\) recurrentes. Obtendremos mayor facilidad para trabajar con esto en la siguiente sección cuando se discutan los valores propios y los vectores propios.

---

Referencia

⁴ Uno podría intentar ingenuamente mostrar que existe un vector de estado estacionario señalando primero que cada fila de\(P\) sumas a 1. El vector de columna satisface\(\boldsymbol{e}=(1,1, \ldots, 1)^{\top}\) entonces la ecuación del vector propio\(\boldsymbol{e}=[P] \boldsymbol{e}\). Por lo tanto, también debe haber un eigenvector izquierdo satisfactorio\(\boldsymbol{\pi}[P]=\boldsymbol{\pi}\). El problema aquí es mostrar que\(\boldsymbol{\pi}\) es real y no negativo.

⁵ Este es esencialmente el teorema de Frobenius para matrices irreducibles no negativas, especializadas en cadenas de Markov. Una matriz no negativa\([P]\) es irreducible si su gráfica (que contiene un borde de nodo\(i\) a\(j\) si\(P_{i j}>0\)) es la gráfica de una cadena recurrente de Markov. No hay restricción de que cada fila de\([P]\) sumas a 1. La prueba del teorema de Frobenius requiere un análisis bastante intrincado y parece ser mucho más compleja que la simple prueba aquí para las cadenas de Markov. Una prueba del teorema general de Frobenius se puede encontrar en [10].