3.5: Cadenas de Markov con Recompensas

Supongamos que cada estado en una cadena de Markov está asociado con una recompensa,\(r_{i}\). A medida que la cadena Markov avanza de estado a estado, hay una secuencia asociada de recompensas que no son independientes, sino que están relacionadas por las estadísticas de la cadena Markov. El concepto de recompensa en cada estado ¹¹ es bastante gráfico para modelar las ganancias corporativas o el desempeño de la cartera, y también es útil para estudiar el retraso en la cola, el tiempo hasta que se ingresa a algún estado dado, y muchos otros fenómenos. La recompensa\(r_{i}\) asociada a un estado también podría verse como un costo o cualquier función dada de valor real del estado.

En la Sección 3.6, estudiamos la programación dinámica y la teoría de la decisión de Markov. Estos temas incluyen a un “tomador de decisiones”, “creador de políticas” o “control” que modifica tanto las probabilidades de transición como las recompensas en cada prueba de la 'cadena Markov'. El tomador de decisiones intenta maximizar la recompensa esperada, pero generalmente se enfrenta a un compromiso entre la recompensa inmediata y la recompensa a más largo plazo que surge de la elección de probabilidades de transición que conducen a estados de 'alta recompensa'. Este es un problema mucho más desafiante que el estudio actual de las cadenas de Markov con recompensas, pero una comprensión profunda del problema actual proporciona la maquinaria para comprender también la teoría de la decisión de Markov.

La recompensa esperada en estado estacionario por unidad de tiempo, asumiendo una sola clase recurrente de estados, se define como la ganancia, expresada como\(g=\sum_{i} \pi_{i} r_{i}\) donde\(\pi_{i}\) está la probabilidad de estado estacionario

Ejemplos de Cadenas Markov con Recompensas

Los siguientes ejemplos demuestran que es importante comprender el comportamiento transitorio de las recompensas así como los promedios a largo plazo. Este comportamiento transitorio resultará aún más importante cuando estudiemos la teoría de la decisión de Markov y la programación dinámica.

Ejemplo 3.5.1: Tiempo esperado de primer paso

Los tiempos de primer paso, es decir, el número de pasos dados al pasar de un estado dado, digamos\(i\), a otro, digamos 1, son frecuentemente de interés para las cadenas de Markov, y aquí resolvemos para el valor esperado de esta variable aleatoria.

Solución

Dado que el tiempo de primer paso es independiente de las transiciones posteriores a la primera entrada al estado 1, podemos modificar la cadena para convertir el estado final, digamos el estado 1, en un estado de captura (un estado de captura\(i\) es un estado del que no hay salida, es decir, para el cual\(P_{i i}=1\)). Es decir, modificamos\(P_{11}\) a 1 y\(P_{1 j}\) a 0 para todos\(j \neq 1\). Dejamos\(P_{i j}\) sin cambios para todos\(i \neq 1\) y para todos\(j\) (ver Figura 3.6). Esta modificación de la cadena no cambiará la probabilidad de ninguna secuencia de estados hasta el punto en que se ingrese primero al estado 1.

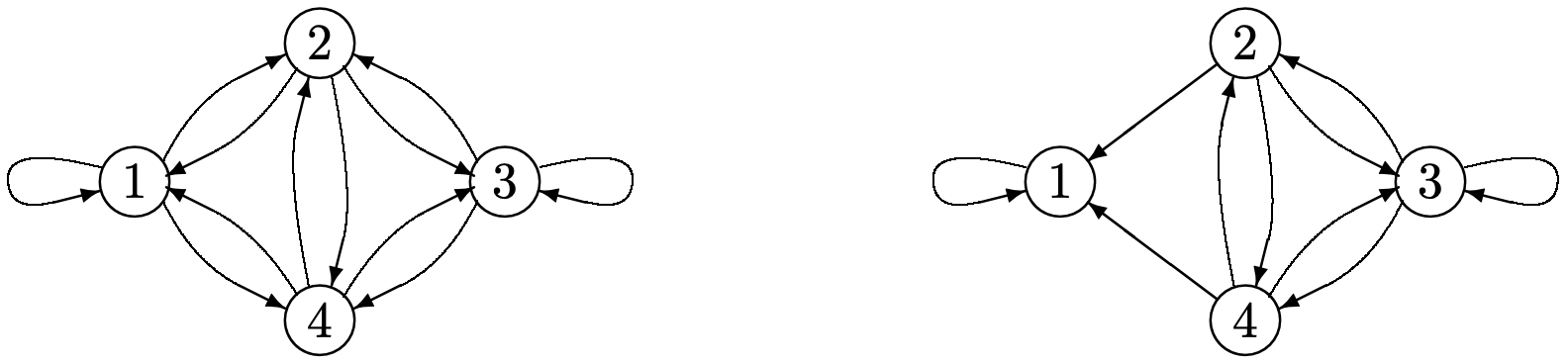Figura 3.6: La conversión de una cadena recurrente de Markov con M = 4 en una cadena para la cual el estado 1 es un estado de captura, es decir, se han eliminado los arcos salientes del nodo 1.

\(v_{i}\)Sea el número esperado de pasos para llegar primero al estado 1 iniciando en estado\(i \neq 1\). Este número de pasos incluye el primer paso más el número esperado de pasos restantes para alcanzar el estado 1 comenzando desde cualquier estado que se ingrese a continuación (si el estado 1 es el siguiente estado ingresado, este número restante es 0). Así, para la cadena en la Figura 3.6, tenemos las ecuaciones

\ (\ begin {alineado}
v_ {2} &=1+P_ {23} v_ {3} +P_ {24} v_ {4}\\
v_ {3} &=1+P_ {32} v_ {2} +P_ {33} v_ {3} +P_ {34} v_ {4}\\
v_ {4} &=1+P_ {42} _ {2} +P_ {43} v_ {3}
\ final {alineado}\)

Para una cadena arbitraria de M estados donde 1 es un estado de captura y todos los demás estados son transitorios, este conjunto de ecuaciones se convierte en

\[v_{i}=1+\sum_{j \neq 1} P_{i j} v_{j} ; \quad i \neq 1\label{3.31} \]

Si definimos\(r_{i}=1\) para\(i \neq 1\) y\(r_{i}=0\) para\(i=1\), entonces\(r_{i}\) es una recompensa unitaria por no ingresar aún al estado de captura, y\(v_{i}\) es la recompensa agregada esperada antes de ingresar al estado de captura. Así, al tomar\(r_{1}=0\), la recompensa cesa al entrar en el estado de captura, y\(v_{i}\) es la recompensa transitoria esperada, es decir, el tiempo esperado de primer paso de estado\(i\) a estado 1. Tenga en cuenta que en este ejemplo, las recompensas ocurren solo en estados transitorios. Dado que los estados transitorios tienen cero probabilidades de estado estacionario, la ganancia en estado estacionario por unidad de tiempo,\(g=\sum_{i} \pi_{i} r_{i}\), es 0.

Si definimos\(v_{1}=0\), entonces (3.31), junto con\(v_{1}=0\), tiene la forma vectorial

\[\boldsymbol{v}=\boldsymbol{r}+[P] \boldsymbol{v} ; \quad v_{1}=0\label{3.32} \]

Para una cadena de Markov con M estados,\ ref {3.31} es un conjunto de M − 1 ecuaciones en las variables M − 1\(v_{2}\) a\(v_{M}\). La ecuación\(\boldsymbol{v}=\boldsymbol{r}+[P] \boldsymbol{v}\) es un conjunto de M ecuaciones lineales, de las cuales la primera es la ecuación vacía\(v_{1}=0+v_{1}\), y, con\(v_{1}=0\), la última M − 1 corresponde a (3.31). No es difícil demostrar que\ ref {3.32} tiene una solución única para\(\boldsymbol{v}\) bajo la condición de que los estados 2 a M sean todos transitorios y 1 sea un estado de atrapamiento, pero lo demostramos más adelante, en el Teorema 3.5.1, bajo circunstancias más generales.

Ejemplo 3.5.2

Supongamos que una cadena de Markov tiene M estados\(\{0,1, \ldots, \mathrm{M}-1\}\),, y que el estado representa el número de clientes en un sistema de cola de tiempo entero. Supongamos que deseamos encontrar la suma esperada de los tiempos de espera del cliente, comenzando por\(i\) los clientes en el sistema en algún momento dado\(t\) y terminando en el primer instante en que el sistema se vuelve inactivo. Es decir, para cada uno de los\(i\) clientes en el sistema en el momento\(t\), el tiempo de espera se cuenta desde\(t\) que ese cliente sale del sistema. Por cada nuevo cliente que ingresa antes de que el sistema se vuelva inactivo, el tiempo de espera se cuenta desde la entrada hasta la salida.

Solución

Cuando discutimos el teorema de Little en la Sección 4.5.4, se verá que esta suma de tiempos de espera es igual a la suma sobre\(\tau\) del estado\(X_{\tau}\) en el momento\(\tau\), tomada desde\(\tau=t\) hasta la primera vez posterior que el sistema está vacío.

Al igual que en el ejemplo anterior, modificamos la cadena de Markov para hacer del estado 0 un estado de trampeo y suponemos que los demás estados son entonces todos transitorios. Tomamos\(r_{i}=i\) como la “recompensa” en estado\(i\), y\(v_{i}\) como la recompensa agregada esperada hasta que se ingrese al estado de trampeo. Utilizando el mismo razonamiento que en el ejemplo anterior,\(v_{i}\) es igual a la recompensa inmediata\(r_{i}=i\) más la recompensa agregada esperada de cualquier estado que se ingrese a continuación. Así\(v_{i}=r_{i}+\sum_{j \geq 1} P_{i j} v_{j}\). Con\(v_{0}=0\), esto es\(\boldsymbol{v}=\boldsymbol{r}+[P] \boldsymbol{v}\). Esto tiene una solución única para\(\boldsymbol{v}\), como se mostrará más adelante en el Teorema 3.5.1. Este mismo análisis es válido para cualquier elección de recompensa\(r_{i}\) por cada estado transitorio\(i\); la recompensa en el estado de captura debe ser 0 para mantener finita la recompensa agregada esperada.

En los ejemplos anteriores, la cadena de Markov se convierte en un estado de trampeo con ganancia cero, y así la recompensa esperada es un fenómeno transitorio sin recompensa tras entrar en el estado de captura. Ahora nos fijamos en el caso más general de una unichain. En este caso más general, puede haber alguna ganancia por unidad de tiempo, junto con alguna recompensa transitoria esperada dependiendo del estado inicial. Primero analizamos la ganancia agregada sobre un número finito de unidades de tiempo, proporcionando así una manera limpia de ir al límite.

Ejemplo 3.5.3

El ejemplo de la Figura 3.7 proporciona una apreciación intuitiva del problema general. Tenga en cuenta que la cadena tiende a persistir en cualquier estado en el que se encuentre. Así, si la cadena inicia en el estado 2, no sólo se logra una recompensa inmediata de 1, sino que existe una alta probabilidad de recompensas unitarias adicionales en muchas transiciones sucesivas. Así, el valor agregado de comenzar en el estado 2 es considerablemente mayor que la recompensa inmediata de 1. Por otro lado, vemos a partir de la simetría que la ganancia por unidad de tiempo, a lo largo de un largo periodo de tiempo, debe ser la mitad.

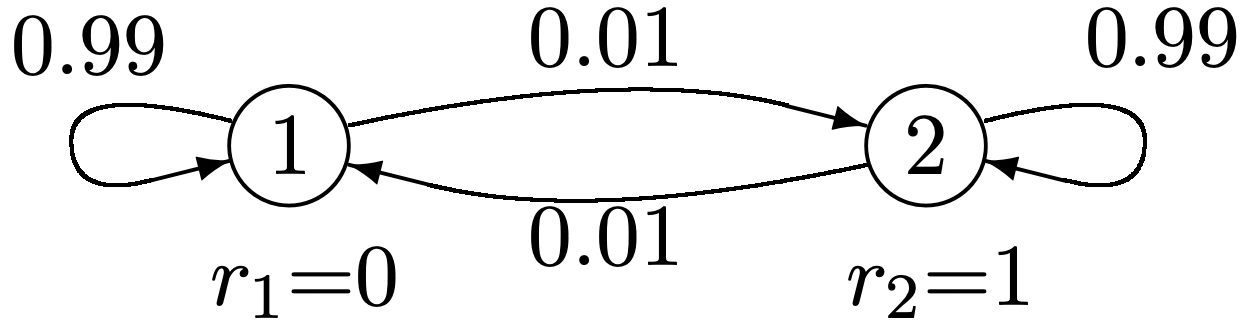Figura 3.7: Cadena de Markov con recompensas y ganancia en estado estacionario distinto de cero.

Recompensa agregada esperada en múltiples transiciones

Volviendo al caso general, dejar\(X_{m}\) ser el estado en el momento\(m\) y dejar\(R_{m}=R\left(X_{m}\right)\) ser la recompensa en ese\(m\), es decir, si el valor muestral de\(X_{m}\) es\(i\), entonces\(r_{i}\) es el valor muestral de\(R_{m}\). Condicionado en\(X_{m}=i\), la recompensa agregada esperada\(v_{i}(n)\) sobre\(n\) las pruebas de\(X_{m}\) a\(X_{m+n-1}\) es

\ (\ begin {alineado}
v_ {i} (n) &=\ mathrm {E}\ izquierda [R\ izquierda (X_ {m}\ derecha) +R\ izquierda (X_ {m+1}\ derecha) +\ cDots+R\ izquierda (X_ {m+n-1}\ derecha)\ mediados X_ {m} =i\ derecha]\\
&=r_ {i} +\ suma_ {j} P_ {i j} r_ {j} +\ cdots+\ suma_ {j} P_ {i j} ^ {n-1} r_ {j}
\ final {alineado}\)

Esta expresión no depende de la hora de inicio\(m\) debido a la homogeneidad de la cadena Markov. Dado que da la recompensa esperada para cada estado inicial\(i\), se puede combinar en la siguiente expresión vectorial\(\boldsymbol{v}(n)=\left(v_{1}(n), v_{2}(n), \ldots, v_{\mathrm{M}}(n)\right)^{\top}\),

\[\boldsymbol{v}(n)=\boldsymbol{r}+[P] \boldsymbol{r}+\cdots+\left[P^{n-1}\right] \boldsymbol{r}=\sum_{h=0}^{n-1}\left[P^{h}\right] \boldsymbol{r}\label{3.33} \]

donde\(\boldsymbol{r}=\left(r_{1}, \ldots, r_{\mathrm{M}}\right)^{\top}\) y\(P^{0}\) es la matriz de identidad. Ahora supongamos que la cadena de Markov es una unicadena ergódica. Entonces\(\lim _{n \rightarrow \infty}[P]^{n}=\boldsymbol{e} \boldsymbol{\pi}\) y\(\lim _{n \rightarrow \infty}[P]^{n} \boldsymbol{r}=\boldsymbol{e} \boldsymbol{\pi} \boldsymbol{r}=g \boldsymbol{e}\) dónde\(g=\boldsymbol{\pi r}\) está la recompensa en estado estacionario por unidad de tiempo. Si\(g \neq 0\), entonces\(\boldsymbol{v}(n)\) cambia por aproximadamente\(g \boldsymbol{e}\) para cada unidad de aumento en\(n\), por lo que\(\boldsymbol{v}(n)\) no tiene un límite como\(n \rightarrow \infty\). Como se muestra a continuación, sin embargo,\(\boldsymbol{v}(n)-n g \boldsymbol{e}\) tiene un límite, dado por

\[\lim _{n \rightarrow \infty}(\boldsymbol{v}(n)-n g \boldsymbol{e})=\lim _{n \rightarrow \infty} \sum_{h=0}^{n-1}\left[P^{h}-\boldsymbol{e} \boldsymbol{\pi}\right] \boldsymbol{r}\label{3.34} \]

Para ver que este límite existe, anote de\ ref {3.26} que se\(\epsilon>0\) puede elegir lo suficientemente pequeño que\(P_{i j}^{n}-\pi_{j}=o(\exp (-n \epsilon))\) para todos los estados\(i\),\(j\) y todos\(n \geq 1\). Así\(\sum_{h=n}^{\infty}\left(P_{i j}^{h}-\pi_{j}\right)=o(\exp (-n \epsilon))\) también. Esto demuestra que los límites a cada lado de\ ref {3.34} deben existir para una unicadena ergódica.

El límite en\ ref {3.34} es un vector sobre los estados de la cadena de Markov. Este vector da la ventaja asintótica esperada relativa de iniciar la cadena en un estado relativo a otro. Esta es una cantidad importante tanto en la siguiente sección como en el resto de ésta. Se llama el vector de ganancia relativa y se denota por\(\boldsymbol{w}\),

\ [\ comenzar {alineado}
\ negritasímbolo {w} &=\ lim _ {n\ fila derecha\ infty}\ suma_ {h=0} ^ {n-1}\ izquierda [P^ {h} -\ negritasímbolo {e}\ negritasímbolo {\ pi}\ derecha]\ negritasímbolo {r} & (3.35)\
&=\ lim _ {n\ fila derecha\ infty} (\ negridsymbol {v} (n) -n g\ negridsymbol {e}). & (3.36)
\ final {alineado}\ nonumber\]

Nota de\ ref {3.36} que si\(g>0\), entonces\(ng\boldsymbol{e}\) aumenta linealmente con\(n\) y y\(\boldsymbol{v}(n)\) debe aumentar asintóticamente linealmente con\(n\). Así, el vector de ganancia relativa\(\boldsymbol{w}\) se vuelve pequeño en relación con ambos\(ng\boldsymbol{e}\) y\(\boldsymbol{v}(n)\) para grandes\(n\). Como veremos, sigue siendo\(\boldsymbol{w}\) importante, particularmente en el siguiente apartado sobre las decisiones de Markov.

Podemos tener algo de idea\(\boldsymbol{w}\) y cómo\(v_{i}(n)-n \pi_{i}\) converge a\(w_{i}\) partir del Ejemplo 3.5.3 (como se describe en la Figura 3.7). Ya que esta cadena tiene sólo dos estados,\(\left[P^{n}\right]\) y se\(v_{i}(n)\) puede calcular fácilmente a partir de (3.28). El resultado se tabula en la Figura 3.8, y se ve numéricamente eso\(\boldsymbol{w}=(-25,+25)^{\top}\). La ventaja bastante significativa de comenzar en el estado 2 en lugar de 1, sin embargo, requiere cientos de transiciones antes de que la ganancia sea completamente aparente.

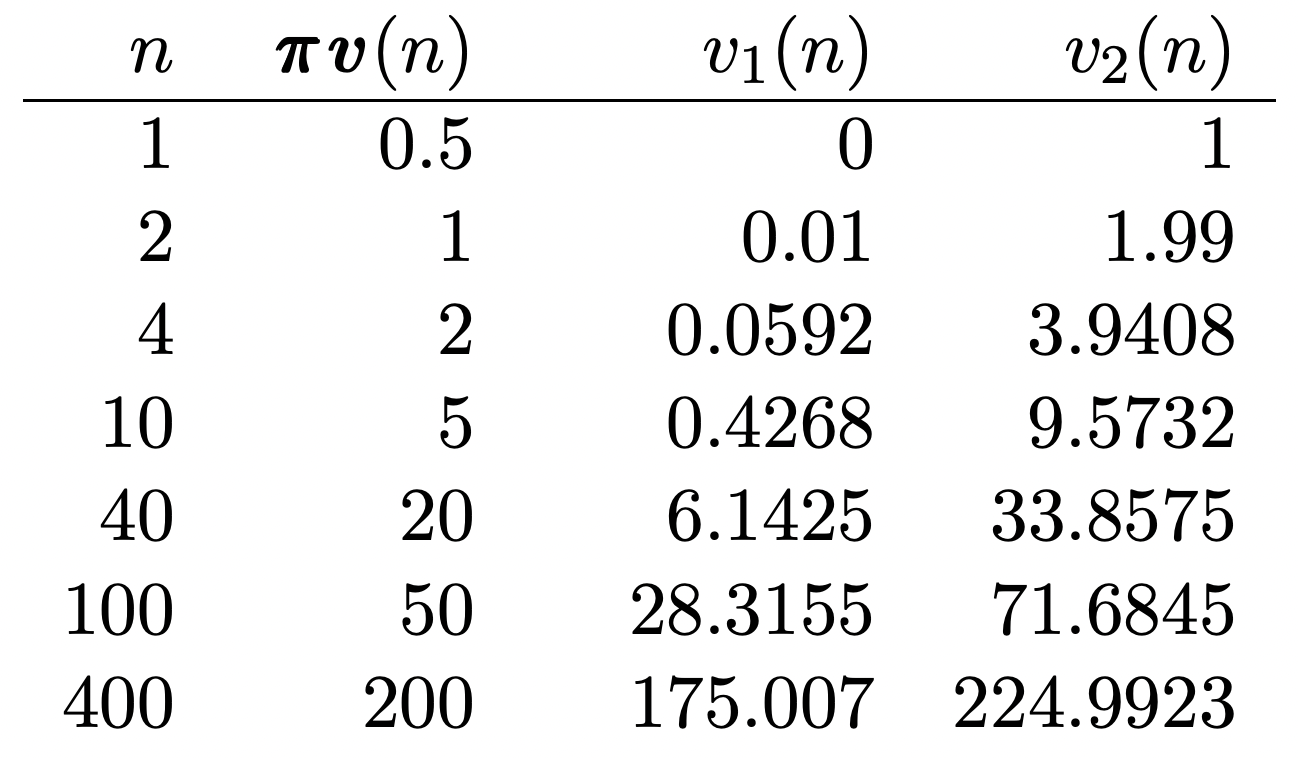Figura 3.8: La recompensa agregada esperada, en función del estado inicial y etapa, para el ejemplo de la figura 3.7. Tenga en cuenta eso\(\boldsymbol{w}=(-25,+25)^{\top}\), pero la convergencia es bastante lenta.

Este ejemplo también muestra que es algo inconveniente calcular a\(\boldsymbol{w}\) partir de (3.35), y este inconveniente crece rápidamente con el número de estados. Afortunadamente, como se muestra en el siguiente teorema, también se\(\boldsymbol{w}\) puede calcular simplemente resolviendo un conjunto de ecuaciones lineales.

Teorema 3.5.1

Dejar\([P]\) ser la matriz de transición para una unicadena ergódica. Entonces el vector relativegain\(\boldsymbol{w}\) dado en\ ref {3.35} satisface la siguiente ecuación vectorial lineal.

\[\boldsymbol{w}+g \boldsymbol{e}=[P] \boldsymbol{w}+\boldsymbol{r} \quad \text { and } \boldsymbol{\pi} \boldsymbol{w}=0\label{3.37} \]

Además\ ref {3.37} tiene una solución única si\([P]\) es la matriz de transición para una unicadena (ya sea ergódica o periódica).

Discusión

Para una unicaína ergódica, la interpretación de\(\boldsymbol{w}\) como ganancia relativa asintótica proviene de\ ref {3.35} y (3.36). Para una unicadena periódica,\ ref {3.37} todavía tiene una solución única, pero\ ref {3.35} ya no converge, por lo que la solución a\ ref {3.37} ya no tiene una interpretación limpia como límite asintótico de ganancia relativa. Esta solución todavía se llama vector de ganancia relativa, y puede interpretarse como una ganancia relativa asintótica a lo largo de un periodo, pero lo importante es que esta ecuación tiene una solución única para unichains arbitrarios

Definición 3.5.1

El vector de ganancia relativa\(\boldsymbol{w}\) de una unicadena es el vector único que satisface (3.37).

Prueba

Premultiplicando ambos lados de\ ref {3.35} por\([P]\),

\ (\ comenzar {alineado} {}
[P]\ negritasímbolo {w} &=\ lim _ {n\ fila derecha\ infty}\ suma_ {h=0} ^ {n-1}\ izquierda [P^ {h+1} -\ negritasímbolo {e}\ negritasímbolo {\ pi}\ derecha]\ negritasímbolo {r}\ &=\ lim _ {n\ derecha]\ negrilla {r}\
&=\ lim _ {n\ derecha fila\ infty}\ suma_ {h=1} ^ {n}\ izquierda [P^ {h} -\ negridsymbol {e}\ símbolo en negrilla {\ pi}\ derecho]\ símbolo en negrilla {r}\\
&=\ lim _ {n\ fila derecha\ infty}\ izquierda (\ suma_ {h=0} ^ {n}\ izquierda [P^ {h} -\ negrilla {e}\ símbolo en negrilla {\ pi}\ derecha]\ negrilla {r}\ derecha) -\ izquierda [P^ {0} -\ negrilla {e}\ símbolo en negrilla {\ pi} derecha]\ negridsymbol {r}\\
&=\ negridsymbol {w} -\ izquierda [P^ {0}\ derecha]\ negridsymbol {r} +\ negridsymbol {e}\ negridsymbol {\ pi} \ negridsymbol {r} =\ negridsymbol {w} -\ negridsymbol {r} +g\ negridsymbol {e}
\ end {alineado}\)

Reordenando términos, obtenemos (3.37). Para una unicaína, el valor propio 1 de\([P]\) tiene multiplicidad 1, y la existencia y singularidad de la solución a\ ref {3.37} es entonces un resultado simple en álgebra lineal (ver Ejercicio 3.23).

Las manipulaciones anteriores ocultan la naturaleza intuitiva de (3.37). Para ver la intuición, considere de nuevo el ejemplo del primer paso-tiempo. Dado que todos los estados son transitorios excepto el estado 1,\(\pi_{1}=1\). Ya que\(r_{1}=0\), vemos que la ganancia en estado estacionario es\(g=0\). También, en el modelo más general del teorema,\(v_{i}(n)\) se encuentra la recompensa esperada sobre\(n\) las transiciones que comienzan en estado\(i\), que para el ejemplo de primer paso-tiempo es el número esperado de estados transitorios visitados hasta la\(n\) ésima transición. En otras palabras, la cantidad\(v_{i}\) en el ejemplo del primer paso-tiempo es\(\lim _{n \rightarrow \infty} v_{i}(n)\). Esto quiere decir que el\(\boldsymbol{v}\) in\ ref {3.32} es lo mismo que\(\boldsymbol{w}\) aquí, y se ve que las fórmulas son las mismas con\(g\) set a 0 in (3.37).

La razón por la que la derivación de la recompensa agregada fue tan simple para el primer paso es que no hubo ganancia en estado estacionario en ese ejemplo, y por lo tanto no es necesario separar la ganancia por transición\(g\) de la ganancia relativa\(\boldsymbol{w}\) entre los estados iniciales.

Una forma de aplicar la intuición del\(g=0\) caso al caso general es la siguiente: dado un vector de recompensa\(\boldsymbol{r}\), encontrar la ganancia\(g=\boldsymbol{\pi} \boldsymbol{r}\) en estado estacionario y luego definir un vector de recompensa modificado\(\boldsymbol{r}^{\prime}=\boldsymbol{r}-g \boldsymbol{e}\). Cambiar el vector de recompensa de\(\boldsymbol{r}\) a de esta\(\boldsymbol{r}^{\prime}\) manera no cambia\(\boldsymbol{w}\), pero la ganancia agregada limitante modificada, digamos\(\boldsymbol{v}^{\prime}(n)\) entonces tiene un límite, que es de hecho\(\boldsymbol{w}\). La derivación intuitiva utilizada en\ ref {3.32} nos da de nuevo\(\boldsymbol{w}=[P] \boldsymbol{w}+{\boldsymbol{r}}^{\prime}\). Esto equivale a\ ref {3.37} ya que\(\boldsymbol{r}^{\prime}=\boldsymbol{r}-g \boldsymbol{e}\).

Existen muchas generalizaciones del ejemplo del primer paso-tiempo en el que la recompensa en cada estado recurrente de una unicadena es 0. De esta manera, la recompensa se acumula sólo hasta que se ingresa un estado recurrente. El siguiente corolario proporciona un resultado de monotonicidad sobre el vector relativegain para estas circunstancias que podría parecer obvio ¹². Así simplemente lo declaramos y damos una prueba guiada en el Ejercicio 3.25.

Corolario 3.5.1

Dejar\([P]\) ser la matriz de transición de una unicaína con la clase recurrente\(\mathcal{R}\). Dejar\(\boldsymbol{r} \geq 0\) ser un vector de recompensa para\([P]\) con\(r_{i}=0\) para\(i \in \mathcal{R}\). Entonces el vector de ganancia relativa\(\boldsymbol{w}\) satisface\(\boldsymbol{w} \geq 0\) con\(w_{i}=0\) para\(i \in \mathcal{R}\) y\(w_{i}>0\) para\(r_{i}>0\). Además, si\(\boldsymbol{r}^{\prime}\) y\(\boldsymbol{r}^{\prime \prime}\) son diferentes vectores de recompensa para\([P]\) y\(\boldsymbol{r}^{\prime} \geq \boldsymbol{r}^{\prime \prime}\) con\(r_{i}^{\prime}=r_{i}^{\prime \prime}\) para\(i \in \mathcal{R}\), entonces\(\boldsymbol{w}^{\prime} \geq \boldsymbol{w}^{\prime \prime}\) con\(w_{i}^{\prime}=w_{i}^{\prime \prime}\) para\(i \in \mathcal{R}\) y\(w_{i}^{\prime}>w_{i}^{\prime \prime}\) para\(r_{i}^{\prime}>r_{i}^{\prime \prime}\).

Recompensa agregada esperada con una recompensa final adicional

Frecuentemente, cuando se agrega una recompensa sobre\(n\) las transiciones de una cadena de Markov, es apropiado asignar alguna recompensa agregada\(u_{i}\), digamos, en función del estado final\(i\). Por ejemplo, podría ser particularmente ventajoso terminar en algún estado en particular. Además, si deseamos ver la recompensa agregada sobre\(n+\ell\) las transiciones como la recompensa sobre las primeras\(n\) transiciones más que sobre las siguientes\(\ell\) transiciones, podemos modelar la recompensa esperada sobre las\(\ell\) transiciones finales como recompensa final al final de la primera\(n\) transiciones. Tenga en cuenta que esta recompensa final esperada depende únicamente del estado al final de las primeras\(n\) transiciones.

Como antes, dejemos\(R\left(X_{m+h}\right)\) ser la recompensa a tiempo\(m+h\) para\(0 \leq h \leq n-1\) y\(U\left(X_{m+n}\right)\) ser la recompensa final en el momento\(m+n\), donde\(U(X)=u_{i}\) para\(X=i\). Deja\(v_{i}(n, \boldsymbol{u})\) ser la recompensa esperada de vez\(m\) en cuando\(m+n\), usando la recompensa\(\boldsymbol{r}\) de vez\(m\) en cuando\(m+n-1\) y usando la recompensa final en el\(\boldsymbol{u}\) momento\(m+n\). La recompensa esperada es entonces la siguiente modificación simple de (3.33):

\[\boldsymbol{v}(n, \boldsymbol{u})=\boldsymbol{r}+[P] \boldsymbol{r}+\cdots+\left[P^{n-1}\right] \boldsymbol{r}+\left[P^{n}\right] \boldsymbol{u}=\sum_{h=0}^{n-1}\left[P^{h}\right] \boldsymbol{r}+\left[P^{n}\right] \boldsymbol{u}\label{3.38} \]

Esto simplifica considerablemente si\(\boldsymbol{u}\) se toma como el vector de ganancia relativa\(\boldsymbol{w}\).

Teorema 3.5.2

Dejar\([P]\) ser la matriz de transición de una unicadena y dejar\(\boldsymbol{w}\) ser el vector de ganancia relativa correspondiente. Entonces para cada uno\(n \geq 1\),

\[\boldsymbol{v}(n, \boldsymbol{w})=n g \boldsymbol{e}+\boldsymbol{w}\label{3.39} \]

Además, para un vector de recompensa final arbitrario\(\boldsymbol{u}\),

\[\boldsymbol{v}(n, \boldsymbol{u})=n g \boldsymbol{e}+\boldsymbol{w}+\left[P^{n}\right](\boldsymbol{u}-\boldsymbol{w})\label{3.40} \]

Discusión

Un caso especial importante de\ ref {3.40} surge de establecer la recompensa\(\boldsymbol{u}\) final en 0, dando así la siguiente expresión para\(\boldsymbol{v}(n)\):

\[\boldsymbol{v}(n)=n g \boldsymbol{e}+\boldsymbol{w}-\left[P^{n}\right] \boldsymbol{w}\label{3.41} \]

Para una unicadena ergódica,\(\lim _{n \rightarrow \infty}\left[P^{n}\right]=\boldsymbol{e} \boldsymbol{\pi}\). Dado que\(\boldsymbol{\pi} \boldsymbol{w}=0\) por definición de\(\boldsymbol{w}\), el límite de\ ref {3.41} como\(n \rightarrow \infty\) es

\(\lim _{n \rightarrow \infty}(\boldsymbol{v}(n)-n g \boldsymbol{e})=\boldsymbol{w},\)

que concuerda con (3.36). La ventaja de\ ref {3.41} sobre\ ref {3.36} es que proporciona una expresión explícita\(\boldsymbol{v}(n)\) para cada uno\(n\) y también que continúa manteniendo para una unicadena periódica.

Prueba

Para\(n=1\), vemos de\ ref {3.38} que

\(\boldsymbol{v}(1, \boldsymbol{w})=\boldsymbol{r}+[P] \boldsymbol{w}=g \boldsymbol{e}+\boldsymbol{w},\)

por lo que el teorema está satisfecho para\(n = 1\). Para\(n>1\),

\ (\ begin {alineado}
\ negritasímbolo {v} (n,\ negridsymbol {w}) &=\ suma_ {h=0} ^ {n-1}\ izquierda [P^ {h}\ derecha]\ negridsymbol {r} +\ izquierda [P^ {n}\ derecha]\ negridsymbol {w}\\
&=\ sum_ {h=0} ^ {n-2}\ izquierda [P^ {h}\ derecha]\ negridsymbol {r} +\ izquierda [P^ {n-1}\ derecha] (\ negritasímbolo {r} + [P]\ negridsymbol {w})\\
&=\ suma_ {h=0} ^ {n-2}\ izquierda [P^ {h}\ derecha]\ negridsymbol {r} +\ izquierda [P^ {n-1}\ derecha] (g\ negridsymbol {e} +\ negridsymbol {w})\\
&=\ negritasímbolo {v} (n-1,\ negridsymbol {w}) +g\ negritasímbolo {v} (n-1,\ negritasímbolo {w}) +g\ negritasímbolo {e}.
\ end {alineado}\)

Usando inducción, esto implica (3.39).

Para establecer (3.40), anote de\ ref {3.38} que

\(\boldsymbol{v}(n, \boldsymbol{u})-\boldsymbol{v}(n, \boldsymbol{w})=\left[P^{n}\right](\boldsymbol{u}-\boldsymbol{w})\)

Entonces\ ref {3.40} sigue usando\ ref {3.39} para el valor de\(\boldsymbol{v}(n, \boldsymbol{w})\)

---

Referencia

⁹ Véase Strang [19], por ejemplo, para una descripción más completa de cómo construir una forma de Jordania

¹⁰ Este polinomio es igual a 1 si estos valores propios son simples.

¹¹ Ocasionalmente es más natural asociar las recompensas con las transiciones que con los estados. Si\(r_{i j}\) denota una recompensa asociada con una transición de\(i\) a\(j\) y\(P_{i j}\) denota la probabilidad de transición correspondiente, entonces definir\(r_{i}=\sum_{j} P_{i j} r_{i j}\) esencialmente simplifica estas recompensas de transición a recompensas sobre el estado inicial para la transición. Estas recompensas de transición se ignoran aquí, ya que los detalles agregan complejidad a un tema que es lo suficientemente complejo para un primer tratamiento.

¹² Un contraejemplo obvio si omitimos la condición\(r_{i}=0\) para\(i \in \mathcal{R}\) viene dado por la Figura 3.7 dónde\(\boldsymbol{r}=(0,1)^{\top}\) y\(\boldsymbol{w}=(-25,25)^{\top}\).