6.6: Reversibilidad para procesos de Markov

En la Sección 5.3 sobre reversibilidad para cadenas de Markov,\ ref {5.37} mostró que las probabilidades de transición hacia atrás\(P_{ij}^*\) en estado estacionario satisfacen

\[ \pi_iP_{ij}^* = \pi_j P_{ji} \nonumber \]

Estas ecuaciones son entonces válidas para la cadena incrustada de un proceso de Markov. A continuación, considere las transiciones hacia atrás en el proceso mismo. Dado que el proceso está en estado\(i\), la probabilidad de una transición en un incremento\(\delta\) de tiempo es\(\nu_i\delta+o(\delta)\), y las transiciones en incrementos sucesivos son independientes. Así, si vemos que el proceso va hacia atrás en el tiempo, la probabilidad de una transición en cada incremento\(\delta\) de tiempo es también\(\nu_i\delta+o(\delta)\) con independencia entre incrementos. Así, yendo al límite\(\delta\rightarrow 0\), la distribución del tiempo hacia atrás a una transición es exponencial con parámetro\(\nu_i\). Esto significa que el proceso que va hacia atrás es nuevamente un proceso de Markov con probabilidades de transición\(P_{ij}^*\) y tasas de transición\(\nu_i\). La Figura 6.11 ayuda a ilustrar esto.

Dado que las probabilidades de estado estacionario {\(p_i; i\geq 0\)} para el proceso de Markov están determinadas por

\[ p_i = \dfrac{\pi_i/\nu_i}{\sum_k \pi_k / \nu_k} \nonumber \]

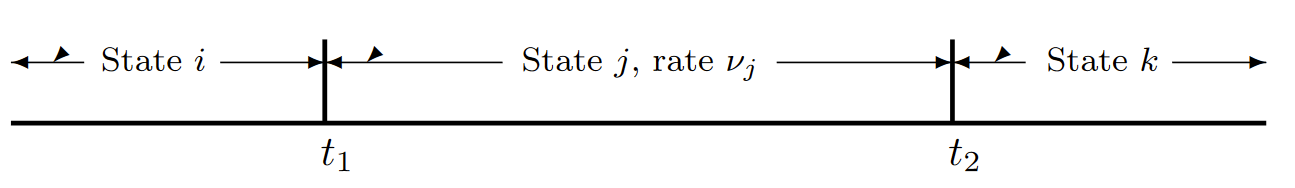
Figura 6.11: El proceso directo entra\( j\) en estado en el momento\(t_1\) y sale en\(t_2\). El proceso hacia atrás entra\(j\) en estado en el momento\(t_2\) y sale en\(t_1\). En cualquier función de muestra, como se ilustra, el intervalo en un estado dado es el mismo en el proceso hacia adelante y hacia atrás. Dado\(X(t) = j\), el tiempo de avance a la siguiente transición y el tiempo hacia atrás a la transición anterior son cada uno exponenciales con tasa\(\nu_j\).

y dado que\(\{\pi_i; i\geq 0\}\) y\(\{\nu_i;i\geq 0\}\) son los mismos para los procesos hacia adelante y hacia atrás, vemos que las probabilidades de estado estacionario en el proceso atrasado de Markov son las mismas que las probabilidades de estado estacionario en el proceso hacia adelante. Este resultado también se puede ver por la correspondencia entre las funciones de muestra en los procesos hacia adelante y hacia atrás.

Las tasas de transición en el proceso hacia atrás se definen por\(q_{ij}^*= \nu_iP_{ij}^*\). Usando (6.6.1), tenemos

\[ q_{ij}^* = \nu_jP_{ij}^* = \dfrac{\nu_i\pi_jP_{ij}}{\pi_i} = \dfrac{\nu_i\pi_jq_{ij}}{\pi_i \nu_j} \nonumber \]

De (6.6.2), observamos que\(p_j = \alpha \pi_j /\nu_j\) y\(p_i = \alpha\pi_i/\nu_i\) por el mismo valor de\(\alpha\). Así la relación de\(\pi_j /\nu_j\) a\(\pi_i/\nu_i\) es\(p_j /p_i\). Esto simplifica (6.6.3) a\(q_{ij}^*= p_j q_{ji}/p_i\), y

\[ p_iq_{ij}^*=p_jq_{ij} \nonumber \]

Esta ecuación puede ser utilizada como una definición alternativa de las tasas de transición hacia atrás. Para interpretar esto, vamos a\(\delta\) ser un incremento de tiempo esfumantemente pequeño y supongamos que el proceso está en estado estacionario en el momento\(t\). Entonces\(\delta p_jq_{ij} \approx \text{Pr}\{X(t)=j\} \text{Pr} \{X(t+\delta)=i | X(t)=j\} \) mientras que\(\delta p_iq_{ij}^* \approx \text{Pr}\{ X(t+\delta) = i\} \text{Pr}\{ X(t)=j | X(t+\delta ) =i \} \).

Un proceso de Markov se define como reversible si es\(q_{ij}^*= q_{ij}\) para todos\(i, j\). Si la cadena incrustada de Markov es reversible\(i.e.\), (,\(P_{ij}^*= P_{ij}\) para todos\(i, j\)), entonces uno puede repetir los pasos anteriores usando\(P_{ij}\) y\(q_{ij}\) en lugar de\(P_{ij}^*\) y\( q_{ij}^*\) ver eso\(p_iq_{ij} = p_j q_{ji}\) para todos\(i, j\). Así, si la cadena incrustada es reversible, el proceso también lo es. De igual manera, si el proceso de Markov es reversible, el argumento anterior se puede revertir para ver que la cadena incrustada es reversible. Así, tenemos el siguiente lema útil.

Lema 6.6.1. Supongamos que las probabilidades de estado estacionario\(\{p_i; i\geq 0\}\) existen en un proceso irreducible de Markov (\(i.e.\), (6.2.17) tiene una solución y\(\sum p_i\nu_i < \infty\)). Entonces el proceso de Markov es reversible si y solo si la cadena incrustada es reversible.

Se pueden encontrar las probabilidades de estado estacionario de un proceso reversible de Markov y simultáneamente mostrar que es reversible por el siguiente teorema útil (que es directamente análogo al Teorema 5.3.2 del capítulo 5).

Teorema 6.6.1. Para un proceso irreducible de Markov, supongamos que\(\{ p_i; i\geq 0\}\) es un conjunto de números no negativos que suman a 1 \(\sum_i p_i\nu_i\leq \infty\), satisfactorios y satisfactorios

\[ p_iq_{ij} = p_jq_{ji} \qquad for \, all \, i,j \nonumber \]

Entonces\(\{ p_i;i\geq 0\}\) es el conjunto de probabilidades de estado estacionario para el proceso,\(p_i > 0\) para todos\(i\), el proceso es reversible, y la cadena incrustada es recurrente positiva.

Prueba: Sumando (6.6.5) sobre\(i\), obtenemos

\[ \sum_i p_iq_{ij} = p_j\nu_j \qquad \text{for all } j \nonumber \]

Estas, junto con\(\sum_i p_i = 1\) son las ecuaciones de estado estacionario para el proceso. Estas ecuaciones tienen una solución, y por el Teorema 6.2.2,\(p_i > 0\) para todos\(i\), la cadena incrustada es recurrente positiva, y\(p_i = \lim_{t\rightarrow \infty} \text{Pr}\{X(t) = i\}\). Comparando (6.6.5) con (6.6.4), vemos eso\(q_{ij} = q_{ij}^*\), por lo que el proceso es reversible.

\(\square \)

Hay muchos procesos irreducibles de Markov que no son reversibles pero para los cuales el proceso atrasado tiene propiedades interesantes que se pueden deducir, al menos intuitivamente, del proceso hacia adelante. Las redes Jackson (que se estudiarán en breve) y muchas redes más complejas de colas entran en esta categoría. El siguiente teorema simple nos permite utilizar cualquier combinación de razonamiento intuitivo y ilusión que deseamos para adivinar tanto las tasas de transición\( q_{ij}^*\) en el proceso hacia atrás como las probabilidades de estado estacionario, y luego verificar rigurosamente que la conjetura es correcta. Uno podría pensar que adivinar de alguna manera no es científico, pero de hecho, el arte de adivinar educado y razonamiento intuitivo conduce a gran parte de la mejor investigación.

Teorema 6.6.2. Para un proceso irreducible de Markov, supongamos que un conjunto de números positivos\(\{p_i; i\geq 0\}\) satisfacen\(\sum_i p_i = 1\) y\(\sum_i p_i\nu_i < \infty\). También suponga que un conjunto de números no negativos\(\{ q_{ij}^*\}\) satisface los dos conjuntos de ecuaciones

\[ \begin{align} &\sum_j q_{ij} = \sum_j q_{ij}^* \qquad for \, all \, i \\ &p_iq_{ij} = p_jq_{ji}^* \qquad for \, all \, i,j \end{align} \nonumber \]

Entonces\(\{p_i\}\) es el conjunto de probabilidades de estado estacionario para el proceso,\(p_i > 0\) para todos\(i\), la cadena incrustada es recurrente positiva, y\(\{ q_{ij}^*\}\) es el conjunto de tasas de transición en el proceso hacia atrás.

Prueba: Suma (6.6.7) sobre\(i\). Usando el hecho de que\(\sum_j q_{ij} = \nu_i\) y usando (6.6.6), obtenemos

\[ \sum_i p_iq_{ij} = p_j\nu_j \qquad \text{for all } j \nonumber \]

Estas, junto con\(\sum_i p_i = 1\), son las ecuaciones de estado estacionario para el proceso. Estas ecuaciones tienen así una solución, y por el Teorema 6.2.2,\(p_i > 0\) para todos\(i\), la cadena incrustada es recurrente positiva, y\(p_i = \lim_{t\rightarrow \infty} \text{Pr}\{X(t) = i\}\). Finalmente,\(q_{ij}^*\) como lo da (6.6.7) es la tasa de transición hacia atrás dada por (6.6.4) para todos\(i, j\).

\(\square\)

Vemos que el Teorema 6.6.1 es solo un caso especial del Teorema 6.6.2 en el que la conjetura al respecto\(q_{ij}^*\) es que\(q_{ij}^*= q_{ij}\).

Los procesos de nacimiento y muerte son todos reversibles si existen las probabilidades de estado estacionario. Para ver esto, tenga en cuenta que la Ecuación (6.5.1) (la ecuación para encontrar las probabilidades de estado estacionario) es justa (6.6.5) aplicada al caso especial de los procesos de nacimiento y muerte. Debido a la importancia de esto, lo declaramos como teorema.

Teorema 6.6.3. Para un proceso de nacimiento y muerte, si hay una solución\(\{p_i; i\geq 0\}\) a (6.5.1) con\(\sum_i p_i = 1\) y\(\sum_i p_i\nu_i < \infty\), entonces el proceso es reversible, y la cadena incrustada es positiva recurrente y reversible.

Dado que el proceso de cola M/M/1 es un proceso de nacimiento a muerte, también es reversible. El teorema de Burke, que se dio como Teorema 5.4.1 para colas M/M/1 de tiempo muestreado, ahora se puede establecer para colas M/M/1 de tiempo continuo. Tenga en cuenta que el teorema aquí contiene una parte extra, la parte c).

Teorema 6.6.4 (Teorema de Burke) Dado un sistema de colas M/M/1 en estado estacionario con\(\lambda < \mu\),

a) el proceso de salida es Poisson con tarifa\(\lambda\)

b) el estado\( X(t)\) en cualquier momento\(t\) sea independiente de las salidas anteriores a\(t\), y

c) para el servicio FCFS, dado que un cliente sale a tiempo\(t\), la hora de llegada de ese cliente es independiente de las salidas anteriores a\( t\).

Prueba: Las pruebas de las partes a) y b) son las mismas que la prueba del teorema de Burke para el tiempo muestreado, Teorema 5.4.1, y por lo tanto no se repetirán. Para la parte c), tenga en cuenta que con el servicio FCFS, el\(m^{th}\) cliente que llegue al sistema también es el\(m^{th}\) cliente a partir. La Figura 6.12 ilustra que la asociación entre llegadas y salidas es la misma en el sistema hacia atrás que en el sistema hacia adelante (aunque el pedido del cliente se invierte en el sistema hacia atrás). En el sistema de avance, movimiento a la derecha, dejó\(\tau\) ser la época de alguna llegada dada. Los clientes que llegan después de\(\tau\) esperar detrás de la llegada dada en la cola, y no tienen ningún efecto en el servicio del cliente dado. Por lo tanto, el intervalo desde\(\tau\) la finalización del servicio al cliente dado es independiente de las llegadas posteriores\(\tau\).

Dado que el sistema hacia atrás, en movimiento a la izquierda, es también una cola M/M/1, el intervalo desde una llegada hacia atrás dada, digamos en época\( t\), moviéndose a la izquierda hasta la salida correspondiente, es independiente de las llegadas a la izquierda de\(t\). A partir de la correspondencia entre las funciones de muestra en los sistemas de movimiento derecho y movimiento izquierdo, dada una salida\(t\) en época en el sistema de movimiento derecho, las salidas antes del tiempo\(t\) son independientes de la época de llegada del cliente dado que sale a\(t\); esto completa la prueba.

\(\square\)

La parte c) del teorema de Burke no se aplica a las colas M/M/1 de tiempo muestreado porque el modelo de tiempo muestreado no permite tanto una llegada como una salida en el mismo incremento de tiempo.

Tenga en cuenta que la prueba del teorema de Burke (incluyendo las partes a y b de la Sección 5.4) no hace uso del hecho de que la tasa de transición\(q_{i,i-1}=\mu\) para\(i\geq 1\) en la cola M/M/1. Así, el teorema de Burke sigue siendo cierto para cualquier proceso de Markov de nacimiento y muerte en estado estacionario para el cual\(q_{i,i+1} = \lambda\) para todos\(i\geq 0\). Por ejemplo, las partes a y b son válidas para las colas M/m/m; la parte c también es válida (ver [22]), pero el argumento aquí no es adecuado ya que el primer cliente en ingresar al sistema podría no ser el primero en salir.

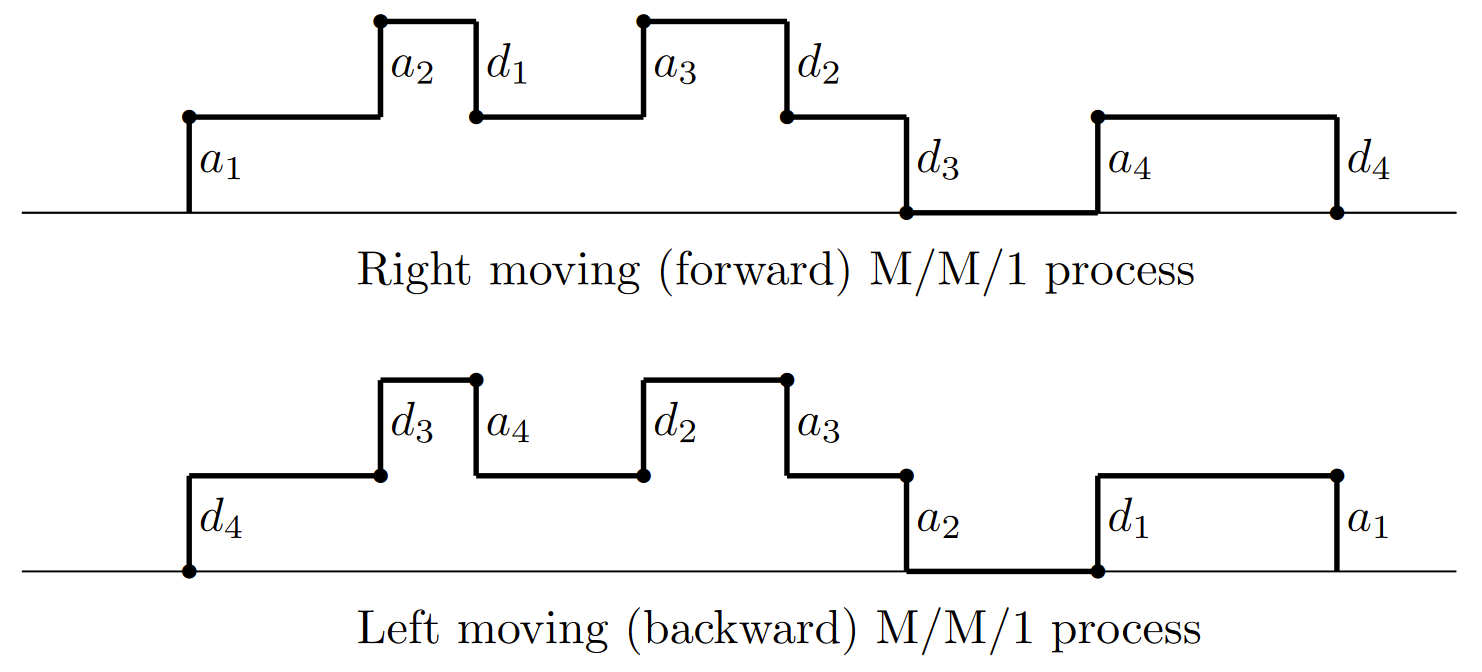
Figura 6.12: Llegadas y salidas de FCFS en procesos M/M/1 en movimiento derecho e izquierdo.

A continuación mostramos cómo se puede utilizar el teorema de Burke para analizar un conjunto de colas en tándem. Como se muestra en la Figura 6.13, contamos con un sistema de colas M/M/1 con llegadas de Poisson a tarifa\(\lambda\) y servicio a tarifa\(μ_1\). Las salidas de este sistema de colas son las llegadas a un segundo sistema de colas, y suponemos que una salida de la cola 1 a la vez ingresa\(t\) instantáneamente al sistema de colas 2 al mismo tiempo\(t\). El segundo sistema de colas tiene un solo servidor y los tiempos de servicio son IID y se distribuyen exponencialmente con tasa\(μ_2\). Los sucesivos tiempos de servicio en el sistema 2 también son independientes de las llegadas a los sistemas 1 y 2, e independientes de los tiempos de servicio en el sistema 1. Ya que ya hemos visto que las salidas del primer sistema son Poisson con tarifa\(\lambda\) las llegadas a la segunda cola son Poisson con tarifa\(\lambda\) Así el segundo sistema también es M/M/1.

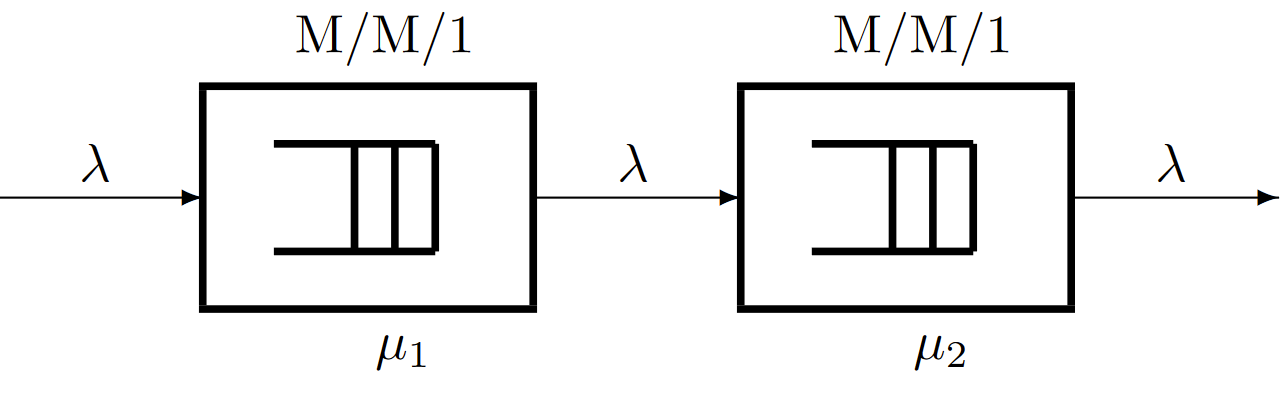
Figura 6.13: Un sistema de cola en tándem. Suponiendo que\(\lambda > \mu_1\) y\(\lambda > \mu_2\), las salidas de cada cola son Poisson de tasa\(\lambda\).

Dejar\( X(t)\) ser el estado del sistema de colas 1 y\(Y (t)\) ser el estado del sistema de colas 2. Dado que\(X(t)\) en el momento\(t\) es independiente de las salidas del sistema 1 anterior a\(t\),\(X(t)\) es independiente de las llegadas al sistema 2 antes de tiempo\(t\). Ya que\(Y (t)\) depende únicamente de las llegadas al sistema 2 antes\(t\) y de los tiempos de servicio que se hayan completado antes de\(t\), vemos que\(X(t)\) es independiente de\(Y (t)\). Esto deja una ligera pregunta sobre lo que sucede en el instante de una salida del sistema 1. Hemos considerado que el estado\(X(t)\) al instante de una salida es el número de clientes que quedan en el sistema 1 sin contar al cliente que sale. También el estado\(Y (t)\) es el estado en el sistema 2 incluyendo la nueva llegada al instante\(t\). El estado\(X(t)\) entonces es independiente de las salidas hasta e inclusive\(t\), de manera que\(X(t)\) y\(Y (t)\) siguen siendo independientes.

A continuación supongamos que ambos sistemas utilizan el servicio FCFS. Considera a un cliente que abandona el sistema 1 a la vez\( t\). El tiempo en que ese cliente llegó al sistema 1, y por lo tanto el tiempo de espera en el sistema 1 para ese cliente, es independiente de las salidas anteriores a\(t\). Esto significa que el estado del sistema 2 inmediatamente antes de que el cliente dado llegue en el momento\(t\) es independiente del tiempo que el cliente pasó en el sistema 1. Por lo tanto, se deduce que el tiempo que el cliente pasa en el sistema 2 es independiente del tiempo empleado en el sistema 1. Así, el tiempo total del sistema que un cliente gasta tanto en el sistema 1 como en el sistema 2 es la suma de dos variables aleatorias independientes.

Este mismo argumento se puede aplicar a más de 2 sistemas de colas en tándem. También se puede aplicar a redes más generales de colas, cada una con servidores individuales con tiempos de servicio distribuidos exponencialmente. La restricción aquí es que no puede haber ningún ciclo de sistemas de colas donde las salidas de cada cola en el ciclo puedan ingresar a la siguiente cola en el ciclo. El problema que plantean dichos ciclos se puede ver fácilmente en el siguiente ejemplo de un sistema de cola único con retroalimentación (ver Figura 6.14).

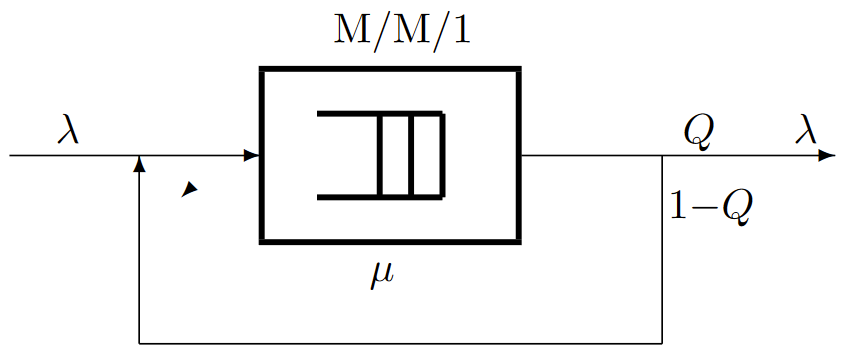
Figura 6.14: Una cola con retroalimentación. Suponiendo que\( μ > \lambda/Q\), la salida exógena es Poisson de tasa\(\lambda\).

Suponemos que el sistema de colas en la Figura 6.14 tiene un único servidor con tiempos de servicio distribuidos exponencialmente IID que son independientes de los tiempos de llegada. Las llegadas exógenas desde fuera del sistema son Poisson con tasa\(\lambda\). Con probabilidad\(Q\), las salidas de la cola dejan todo el sistema y, alternativamente, con probabilidad\(1 - Q\), regresan instantáneamente a la entrada de la cola. Las elecciones sucesivas entre salir del sistema y regresar a la entrada son IID e independientes de las llegadas exógenas y de los tiempos de servicio. La Figura 6.15 muestra una función muestral de las llegadas y salidas en el caso en el que la tasa de servicio\(μ\) es muy superior a la tasa de llegada exógena\(\lambda\). Cada llegada exógena genera un conjunto geométricamente distribuido de salidas y reentradas simultáneas. Por lo tanto, el proceso general de llegada a la cola, contando tanto las llegadas exógenas como la retroalimentación de la salida, no es Poisson. Tenga en cuenta, sin embargo, que si miramos la descripción del proceso de Markov, las salidas que se retroalimentan a la entrada corresponden a los bucles de uno mismo de un estado a sí mismo. Así, el proceso de Markov es el mismo que uno sin los bucles de uno mismo con una tasa de servicio igual a\(μQ\). Así, a partir del teorema de Burke, las salidas exógenas son Poisson con tasa\(\lambda\). También la distribución en estado estacionario de\(X(t)\) es\(P \{X(t) = i\} = (1-\rho ) \rho^i\) donde\(\rho=\lambda /(μQ)\) (asumiendo, por supuesto, eso\(\rho< 1\)).

Figura 6.15: Muestra de ruta de llegadas y salidas para cola con retroalimentación

El sistema de cola en tándem de la Figura 6.13 también puede considerarse como un proceso combinado de Markov en el que el estado en el momento\(t\) es el par\((X(t), Y (t))\). Las transiciones en este proceso corresponden a, primero, llegadas exógenas en las que\(X(t)\) aumenta, segundo, salidas exógenas en las que\(Y (t)\) disminuye, y tercero, transferencias del sistema 1 al sistema 2 en el que\(X(t)\) disminuye y\(Y (t)\) simultáneamente aumenta. El proceso combinado no es reversible ya que no hay transición en la que\(X(t)\) aumente y disminuya\(Y (t)\) simultáneamente. En la siguiente sección, mostramos cómo analizar estos procesos combinados de Markov para redes de colas más generales.