6.7: Jackson Networks

En muchas situaciones de cola, un cliente tiene que esperar en varias colas diferentes antes de completar la transacción deseada y abandonar el sistema. Por ejemplo, cuando vamos al registro de vehículos automotores para obtener una licencia de conducir, debemos esperar en una cola para que se procese la solicitud, en otra cola para pagar la licencia, y en una tercera cola para obtener una fotografía para la licencia. En una instalación informática multiprocesador, un trabajo se puede poner en cola esperando el servicio en un procesador, luego ir a esperar a otro procesador, y así sucesivamente; frecuentemente el mismo procesador se visita varias veces antes de que se complete el trabajo. En una red de datos, los paquetes atraviesan múltiples nodos intermedios; en cada nodo ingresan a una cola esperando su transmisión a otros nodos.

Dichos sistemas son modelados por una red de colas, y las redes Jackson son quizás los modelos más simples de tales redes. En tal modelo, tenemos una red de sistemas de colas\(k\) interconectados a los que llamamos nodos. Cada uno de los\(k\) nodos recibe clientes (\(i.e.\), tareas o trabajos) tanto de fuera de la red (entradas exógenas) como de otros nodos dentro de la red (entradas endógenas). Se supone que las entradas exógenas a cada nodo\(i\) forman un proceso de Poisson de tasa\(r_i\) y que estos procesos de Poisson son independientes entre sí. Por conveniencia analítica, consideramos esto como un único proceso de entrada de Poisson de tasa\(\lambda_0\), con cada entrada yendo independientemente a cada nodo\(i\) con probabilidad\(Q_{0i} =r_i/\lambda_0\).

Cada nodo\(i\) contiene un único servidor, y los sucesivos tiempos de servicio en el nodo\(i\) son variables aleatorias IID con un tiempo de servicio distribuido exponencialmente\(μ_i\). Los tiempos de servicio en cada nodo también son independientes de los tiempos de servicio en todos los demás nodos e independientes de los tiempos de llegada exógenos en todos los nodos. Cuando un cliente completa el servicio en un nodo dado\(i\), ese cliente es enrutado al nodo\(j\) con probabilidad\(Q_{ij}\) (ver Figura 6.16). También es posible que el cliente salga de la red por completo (llamada salida exógena), y esto ocurre con probabilidad\(Q_{i0} = 1 -\sum_{j\geq 1} Q_{ij}\). Para un cliente que sale del nodo\(i\), el siguiente nodo\(j\) es una variable aleatoria con PMF\(\{Q_{ij} , 0 \leq j\leq k\}\).

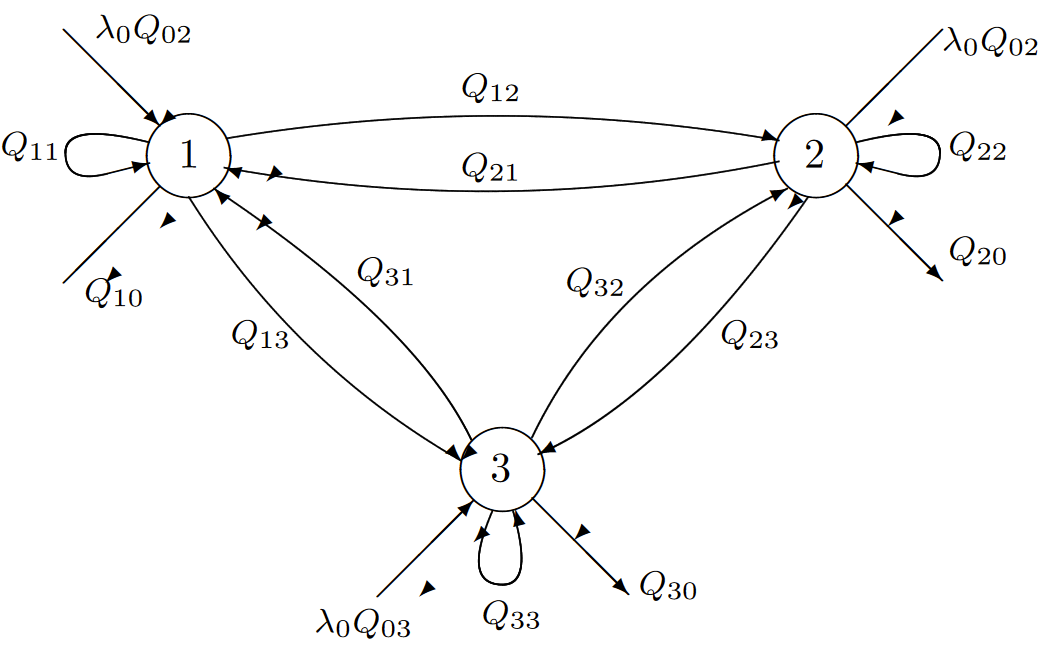
Figura 6.16: Una red Jackson con 3 nodos. Dada una salida del nodo\(i\), la probabilidad de que la salida vaya al nodo\(j\) (o\( j = 0\), para, salga del sistema) es\(Q_{ij}\). Tenga en cuenta que una salida del nodo\(i\) puede volver a ingresar al nodo\(i\) con probabilidad\(Q_{ii}\). La tasa general de llegada exógena es\(\lambda_0\), y, condicionada a una llegada, la probabilidad de que la llegada ingrese al nodo\(i\) es\(Q_{0i}\).

Las elecciones sucesivas del siguiente nodo para los clientes en el nodo\(i\) son IID, independientes del enrutamiento del cliente en otros nodos, independientes de todos los tiempos de servicio e independientes de las entradas exógenas. Notacionalmente, estamos considerando al mundo exterior como un nodo ficticio 0 del que aparecen los clientes y al que desaparecen.

Cuando un cliente es enrutado de nodo\(i\) a nodo\(j\), se supone que el enrutamiento es instantáneo; así, en la época de una salida del nodo\(i\), hay una llegada endógena simultánea al nodo\(j\). Así, un nodo\(j\) recibe llegadas exógenas de Poisson desde fuera del sistema a velocidad\(\lambda_0 Q_{0j}\) y recibe llegadas endógenas de otros nodos de acuerdo con las reglas probabilísticas recién descritas. Podemos visualizar estas llegadas combinadas exógenas y endógenas como atendidas en la moda FCFS, pero realmente no hace dierence en qué orden se atienden, ya que los clientes son estadísticamente idénticos y simplemente dan lugar al servicio en nodo\(j\) a tarifa\(μ_j\) cada vez que hay clientes para ser atendido.

La red de cola Jackson, como se acaba de definir, se describe completamente por la tasa de entrada exógena\(\{μ_i\}\), las tasas de servicio y las probabilidades de enrutamiento\(\{Q_{ij} ; 0 \leq i, j \leq k\}\). La red en su conjunto es un proceso de Markov en el que el estado es un vector\(\boldsymbol{m} = (m_1, m_2, . . . , m_k)\), donde\(m_i, 1 \leq i \leq k\) está el número de clientes en el nodo\(i\). Los cambios de estado ocurren en las llegadas exógenas a los diversos nodos, las salidas exógenas de los diversos nodos y las salidas de un nodo que ingresa a otro nodo. En un intervalo\(\delta\) de tiempo esfumantemente pequeño, dado que el estado al inicio de ese intervalo es\(\boldsymbol{m}\), se\(j\) produce una llegada exógena al nodo en el intervalo con probabilidad\(\lambda_0Q_{0j}\delta\) y cambia el estado a\(\boldsymbol{m}' = \boldsymbol{m} +\boldsymbol{e}_j\) donde\(\boldsymbol{e}_j\) está un vector unitario con uno en posición \(j\). Si\(m_i > 0\),\(i\) se produce una salida exógena del nodo en el intervalo con probabilidad\( μ_iQ_{i0}\delta\) y cambia el estado a\(\boldsymbol{m}' = \boldsymbol{m} -\boldsymbol{e}_i+\boldsymbol{e_j}\). Finalmente, si\(m_i > 0\),\(j\) se produce una salida del nodo\(i\) que ingresa al nodo en el intervalo con probabilidad\(μ_iQ_{ij}\delta\) y cambia el estado a\(\boldsymbol{m}' = \boldsymbol{m} -\boldsymbol{e}_i + \boldsymbol{e}_j \). Así, las tasas de transición vienen dadas por

\[ \begin{align} q_{\boldsymbol{m,m'}} \quad &= \quad \lambda_0Q_{0j} \qquad \text{for } \boldsymbol{m}' = \boldsymbol{m} + \boldsymbol{e}_j, \quad 1\leq i\leq k \\ &= \quad \mu_iQ_{i0} \qquad \, \text{for }\boldsymbol{m}' = \boldsymbol{m}-\boldsymbol{m_i}, \quad m_i>0, \quad 1\leq i\leq k \\ &= \quad \mu_iQ_{ij} \qquad \, \text{for } \boldsymbol{m}' = \boldsymbol{m} - \boldsymbol{e}_i + \boldsymbol{e}_j, \quad m_i>0, \quad 1\leq i,j\leq, k \\ &= \quad 0 \qquad \qquad \text{for all other choices of }\boldsymbol{m}' \nonumber \end{align} \nonumber \]

Obsérvese que una salida del nodo\(i\) que vuelve a ingresar al nodo\(i\) provoca una transición de estado de\(\boldsymbol{m}\) nuevo a estado\(\boldsymbol{m}\); despermitimos tales transiciones en las secciones 6.1 y 6.2, pero demostramos que no causaron problemas en nuestra discusión de uniformización. Es conveniente permitir estas autotransiciones aquí, en parte por la generalidad agregada y en parte para ilustrar que la red de un solo nodo con retroalimentación de la Figura 6.14 es un ejemplo de una red Jackson.

Nuestro objetivo es encontrar las probabilidades de estado estacionario\(p(\boldsymbol{m})\) para este tipo de procesos, y nuestro plan de ataque está de acuerdo con el Teorema 6.6.2; es decir, adivinaremos un conjunto de tasas de transición para el proceso hacia atrás de Markov, utilizarlos para adivinar\(p(\boldsymbol{m})\), y luego verificar que las conjeturas son correctas. Antes de hacer estas conjeturas, sin embargo, debemos conocer un poco más sobre cómo funciona el sistema, para orientar las conjeturas. Definamos\(\lambda_i\) para cada uno\(i, 1 \leq i \leq k\), como la tasa global promedio de tiempo de llegadas al nodo\(i\), incluyendo tanto las llegadas exógenas como endógenas. Dado que\(\lambda_0\) es la tasa de entradas exógenas, podemos interpretar\(\lambda_i/\lambda_0\) como el número esperado de visitas a nodo\(i\) por entrada exógena. Las llegadas endógenas al nodo no\(i\) son necesariamente Poisson, como muestra el ejemplo de una sola cola con retroalimentación, y ni siquiera estamos seguros en este punto de que tal tasa promedio de tiempo exista en algún sentido razonable. Sin embargo, supongamos por el momento que tales tarifas existen y que la tasa promedio de tiempo de salidas de cada nodo es igual a la tasa promedio de llegadas en el tiempo (\(i.e.\), los tamaños de las colas no crecen linealmente con el tiempo). Entonces estas tasas deben satisfacer la ecuación

\[ \lambda_j = \sum^k_{j=0} \lambda_iQ_{ij}; \qquad 1\leq j\leq k \nonumber \]

Para ver esto, tenga en cuenta que\(\lambda_0Q_{0j}\) es la tasa de llegadas exógenas a\(j\). También\(\lambda_i\) es la tasa promedio de tiempo a la que los clientes salen de la cola\(i\), y\(\lambda_iQ_{ij}\) es la tasa a la que los clientes van de nodo\(i\) a nodo\(j\). Así, el lado derecho de (6.7.4) es la suma de las tasas de llegada exógenas y endógenas al nodo\(j\). Obsérvese la distinción entre la tasa promedio de tiempo de los clientes que van de\(i\) a\(j\) in (6.7.4) y la tasa\(q_{\boldsymbol{m,m'}} = μ_iQ_{ij}\) para\(\boldsymbol{m}' = \boldsymbol{m}- \boldsymbol{e}_i+\boldsymbol{e}_j , m_i > 0\) in (6.7.3). La tasa en (6.7.3) está condicionada a un estado\(\boldsymbol{m}\) con\(m_i > 0\), mientras que en (6.7.4) es la tasa promedio de tiempo global, promediada sobre todos los estados.

Obsérvese que\(\{Q_{ij} ; 0 \leq i, j \leq k\}\) forma una matriz estocástica y (6.7.4) es formalmente equivalente a las ecuaciones para las probabilidades de estado estacionario (excepto que las probabilidades de estado estacionario suman a 1). Las ecuaciones habituales para las probabilidades de estado estacionario incluyen una ecuación para\(j = 0\), pero esa ecuación es redundante. Así sabemos que, si hay una ruta entre cada par de nodos (incluyendo el nodo ficticio 0), entonces (6.7.4) tiene una solución para\(\{\lambda_i; 0\leq i\leq k\}\), y esa solución es única dentro de un factor de escala. El valor conocido de\(\lambda_0\) determina este factor de escala y hace que la solución sea única. Tenga en cuenta que no hay que tener cuidado en este punto sobre si estas tasas son medias de tiempo en algún buen sentido, ya que esto se verificará más adelante; sí tenemos que asegurarnos de que (6.7.4) tiene una solución, sin embargo, ya que aparecerá en nuestra solución para\(p(\boldsymbol{m})\). Así asumimos en lo que sigue que existe una ruta entre cada par de nodos, y así que (6.7.4) tiene una solución única en función de\(\lambda_0\).

Ahora hacemos la suposición final necesaria sobre la red, que es la\( μ_i >\lambda_i\) de cada nodo\(i\). Esto resultará ser requerido para que el proceso sea recurrente positivo. También definimos\(\rho_i\) como\(\lambda_i/\mu_i\). Encontraremos que, aunque las entradas a un nodo individual no\(i\) sean Poisson en general, existe una distribución en estado estacionario para el número de clientes en\(i\), y esa distribución es la misma que la de una cola M/M/1 con el parámetro\(\rho_i\).

Ahora considere el proceso de retroceso del tiempo. Hemos visto que sólo tres tipos de transiciones son posibles en el proceso hacia adelante. Primero, hay transiciones de\(\boldsymbol{m}\) a\(\boldsymbol{m}' = \boldsymbol{m} + \boldsymbol{e}_j\) para cualquiera\(j, \, 1 \leq j \leq k\). Segundo, hay transiciones de\(\boldsymbol{m}\) a\(\boldsymbol{m}- \boldsymbol{e}_i\) para cualquiera\(i, 1 \geq i \leq k\), tal que\(m_i > 0\). Tercero, hay transiciones de\(\boldsymbol{m}\) a\(\boldsymbol{m}' = \boldsymbol{m} - \boldsymbol{e}_i + \boldsymbol{e}_j\) para\(1 \leq i, j \leq k\) con\(m_i > 0\). Así, en el proceso hacia atrás, las transiciones de\(\boldsymbol{m}'\) a\( \boldsymbol{m}\) son posibles solo para los\(\boldsymbol{m},\, \boldsymbol{m}'\) pares anteriores. Correspondiente a cada llegada en el proceso hacia adelante, hay una salida en el proceso hacia atrás; para cada salida hacia adelante, hay una llegada hacia atrás; y para cada paso hacia adelante de\(i\) a\(j\), hay un paso hacia atrás de\(j\) a\( i\).

Ahora hacemos la conjetura de que el proceso hacia atrás es en sí mismo una red Jackson con llegadas exógenas de Poisson a tarifas\(\{ \lambda_0Q_{0j}^*\}\), tiempos de servicio exponenciales con tarifas\(\{μ_i\}\) y probabilidades de enrutamiento\(\{Q_{ij}^*\}\). Las probabilidades de enrutamiento hacia atrás\(\{ Q_{ij}^* \}\) deben elegirse para que sean consistentes con las tasas de transición en el proceso hacia adelante. Dado que cada transición de\(i\) a\(j\) en el proceso hacia adelante debe corresponder a una transición de\(j\) a\(i\) en el proceso atrasado, deberíamos haber

\[ \lambda_i Q_{ij} = \lambda_jQ_{ji}^* \quad ; \quad 0\leq i,j \leq k \nonumber \]

Tenga en cuenta que\(\lambda_iQ_{ij}\) representa la velocidad a la que las transiciones hacia adelante van de\(i\) a\(j\), y\(\lambda_i\) representa la velocidad a la que las transiciones hacia adelante salen del nodo\(i\). La ecuación (6.7.5) aprovecha el hecho de que\(\lambda_i\) es también la velocidad a la que las transiciones hacia adelante ingresan al nodo\(i\), y por lo tanto la velocidad a la que las transiciones hacia atrás salen del nodo\(i\). Usando la conjetura de que el sistema de tiempo hacia atrás es una red Jackson con probabilidades de enrutamiento\(\{ Q_{ij}^*; 0 \leq i, j \leq k\}\), podemos anotar las tasas de transición hacia atrás de la misma manera que (6.7.1-6.7.3),

\[ \begin{align} q_{\boldsymbol{m,m'}}^* \quad &= \quad \lambda_0Q_{0j}^* \qquad \text{for } \boldsymbol{m}' =\boldsymbol{m}+\boldsymbol{e}_j \\ &= \quad \mu_iQ_{i0}^* \qquad \, \text{for }\boldsymbol{m}' = \boldsymbol{m}- \boldsymbol{e}_i,m_i > 0, 1\leq i\leq k \\ &= \quad \mu_iQ_{ij}^* \qquad \text{for } \boldsymbol{m}'=\boldsymbol{m}-\boldsymbol{e}_i +\boldsymbol{e}_j, \quad m-i>0, \quad 1 \leq i, \quad j\leq k \end{align} \nonumber \]

Si sustituimos (6.7.5) por (6.7.6) - (6.7.8), obtenemos

\[ \begin{align} q_{\boldsymbol{m,m'}}^* \quad &= \quad \lambda_0Q_{j0} \qquad \qquad \text{for } \boldsymbol{m}' =\boldsymbol{m}+\boldsymbol{e}_j, \quad 1\leq j\leq k \\ &= \quad (\mu_i/\lambda_i)\lambda_0Q_{0i} \quad \text{for }\boldsymbol{m}' = \boldsymbol{m}- \boldsymbol{e}_i,m_i > 0, \quad 1\leq i\leq k \\ &= \quad (\mu_i/\lambda_i)\lambda_jQ_{ji} \quad \text{for } \boldsymbol{m}'=\boldsymbol{m}-\boldsymbol{e}_i +\boldsymbol{e}_j, \qquad m_i>0, \quad 1 \leq i, \quad j\leq k \end{align} \nonumber \]

Esto nos da nuestras hipotéticas tasas de transición hacia atrás en términos de los parámetros de la red Jackson original. Para usar el teorema 6.6.2, debemos verificar que hay un conjunto de números positivos,\(p(\boldsymbol{m})\), satisfactorios\(\sum_m p(\boldsymbol{m}) = 1\) y\(\sum_m \nu_m p_m < \infty\), y un conjunto de números no negativos que\(q_{\boldsymbol{m',m}}^*\) satisfagan los siguientes dos conjuntos de ecuaciones:

\[\begin{align} p(\boldsymbol{m})q_{\boldsymbol{m,m'}} \quad &= \quad p(\boldsymbol{m}')q^*_{\boldsymbol{m',m}} \qquad \text{for all } \boldsymbol{m,m'} \\ \sum_{\boldsymbol{m}}q_{\boldsymbol{m,m'}} \quad &= \quad \sum_{\boldsymbol{m'}} q^*_{\boldsymbol{m,m'}} \qquad \quad \text{for all } \boldsymbol{m}\end{align} \nonumber \]

Verificamos (6.7.12) sustituyendo (6.7.1) - (6.7.3) en el lado izquierdo de (6.7.12) y (6.7.9) - (6.7.11) en el lado derecho. Recordando que\(\rho_i\) se define como\(\lambda_i/\mu_i\), y cancelando términos comunes en cada lado, tenemos

\[ \begin{align} p(\boldsymbol{m}) \quad &= \quad p(\boldsymbol{m}')/\rho_j \qquad \text{for } \boldsymbol{m'}=\boldsymbol{m}+\boldsymbol{e}_j \\ p(\boldsymbol{m}) \quad &= \quad p(\boldsymbol{m'})\rho_i \qquad \, \, \, \text{for } \boldsymbol{m'}=\boldsymbol{m}-\boldsymbol{e}_i, m_i >0 \\ p(\boldsymbol{m}) \quad &= \quad p(\boldsymbol{m'})\rho_i/\rho_j \quad \, \, \text{for } \boldsymbol{m'}=\boldsymbol{m}-\boldsymbol{e}_i+\boldsymbol{e}_j, \qquad m_i>0 \end{align} \nonumber \]

Mirando el caso\(\boldsymbol{m'} =\boldsymbol{m}-\boldsymbol{e}_i\), y usando esta ecuación repetidamente para pasar del estado\((0, 0, . . . , 0)\) a un arbitrario\(\boldsymbol{m}\), obtenemos

\[ p(\boldsymbol{m}) = p(0,0,...,0) \prod^k_{i=1} \rho^{m_i}_i \nonumber \]

Es fácil verificar que (6.7.17) satisface (6.7.14) - (6.7.16) para todas las transiciones posibles. Resumiendo sobre todo\(\boldsymbol{m}\) para resolver\(p(0, 0, . . . , 0)\), obtenemos

\[ \begin{aligned} 1 \quad = \quad \sum_{m_1,m_2,...,m_k} p(\boldsymbol{m}) \quad &= \quad p(0,0,...,0) \sum_{m_1}\rho_1^{m_1}\sum_{m_2}\rho_2^{m_2}...\sum_{m_k}\rho_k^{m_k} \\ &= \quad p(0,0...,0)(1-\rho_1)^{-1}(1-\rho_2)^{-1}...(1-\rho_k)^{-1} \end{aligned} \nonumber \]

Así,\(p(0,0,...,0) = (1-p_1)(1-p_2)...(1-p_k)\), y sustituyendo esto en (6.7.17), obtenemos

\[ p(\boldsymbol{m})=\prod^k_{i=1} p_i(m_i) = \prod^k_{i=1} \left[ (1-\rho_i)\rho_i^{m_i} \right] \nonumber \]

donde\(p_i(m)=(1-\rho_i)\rho^m_i\) está la distribución en estado estacionario de una sola cola M/M/1. Ahora que hemos encontrado la distribución en estado estacionario implicada por nuestra suposición de que el proceso atrasado es una red Jackson, nuestra tarea restante es verificar (6.7.13)

Para verificar (6.7.13),\(i.e.\),\(\sum_{\boldsymbol{m'}} q_{\boldsymbol{m,m'}} = \sum_{\boldsymbol{m'}} q^*_{\boldsymbol{m,m'}} \), primero considerar el lado derecho. Usando (6.7.6) para sumar sobre todo\(\boldsymbol{m}' = \boldsymbol{m} + \boldsymbol{e}_j \), luego (6.7.7) para sumar sobre\(\boldsymbol{m}' = \boldsymbol{m} - \boldsymbol{e}_i\) (para\(i\) tal que\(m_i>0\)), y finalmente (6.7.8) para sumar más\(\boldsymbol{m}' = \boldsymbol{m} - \boldsymbol{e}_i+\boldsymbol{e}_j\), (nuevamente para\(i\) tal que\(m_i > 0\)), obtenemos

\[ \sum_{\boldsymbol{m'}} q^*_{\boldsymbol{m,m'}} = \sum^k_{j=1}\lambda_0Q_{0j}^*+\sum_{i:m_j>0} \mu_iQ_{i0}^* + \sum_{i:m_j>0} \mu_i \sum^k_{j=1} Q_{ij}^* \nonumber \]

Usar el hecho\(Q^*\) es una matriz estocástica, entonces,

\[ \sum_{\boldsymbol{m'}} q^*_{\boldsymbol{m,m'}} = \lambda_0+\sum_{i:m_i>0} \mu_i \nonumber \]

El lado izquierdo de (6.7.13) se puede sumar de la misma manera para obtener el resultado en el lado derecho de (6.7.20), pero podemos ver que este debe ser el resultado simplemente observando que\(\lambda_0\) es la tasa de llegadas exógenas y\(\sum_{i:m_i>0} μ_i\) es la tasa general de terminaciones de servicio en estado\(\boldsymbol{m}\). Tenga en cuenta que esto también verifica que\(\nu_{\boldsymbol{m}} = \sum_{\boldsymbol{m'}} q_{\boldsymbol{m,m'}} \geq \lambda_0 + \sum_i μ_i\), y ya que\(\nu_{\boldsymbol{m}}\) está acotado,\(\sum_{\boldsymbol{m}} \nu_{\boldsymbol{m}} p(\boldsymbol{m}) < \infty\). Dado que se cumplen todas las condiciones del Teorema 6.6.2\(p(\boldsymbol{m})\),, como se da en (6.7.18), da las probabilidades de estado estacionario para la red Jackson. Esto también verifica que el proceso hacia atrás es una red Jackson, y de ahí que las salidas exógenas sean Poisson e independientes.

Aunque las llegadas y salidas exógenas en una red Jackson son Poisson, los procesos endógenos de los clientes que viajan de un nodo a otro normalmente no son Poisson si hay rutas de retroalimentación en la red. Además, aunque (6.7.18) muestra que el número de clientes en los diferentes nodos son variables aleatorias independientes en un momento dado en estado estacionario, generalmente no es cierto que el número de clientes en un nodo a la vez sea independiente del número de clientes en otro nodo en otro momento.

Hay muchas generalizaciones de los argumentos de reversibilidad utilizados anteriormente, y muchas situaciones de red en las que los nodos tienen estados independientes en un tiempo común. Discutimos solo dos de ellos aquí y nos referimos a Kelly, [13], para un tratamiento completo.

Para la primera generalización, supongamos que el tiempo de servicio en cada nodo depende del número de clientes en ese nodo,\(i.e.\),\(μ_i\) se sustituye por\(μ_{i,m_i}\). Tenga en cuenta que esto incluye el tipo de situación M/m/m en la que cada nodo tiene varios servidores exponenciales independientes. Con esta modificación, se modifican las tasas de transición en (6.7.2) y (6.7.3)\(μ_i\) sustituyendo por\(μ_{i,m_i}\). Las hipotéticas tasas de transición hacia atrás se modifican de la misma manera, y el único efecto de estos cambios es sustituir\(\rho_i\) y\(\rho_j\) para cada uno\(i\) y\(j\) en (6.7.14) - (6.7.16) con\(\rho_{i,m_i} =\lambda_i/\mu_{i,m_i}\) y\(\rho_{j,m_j} = \lambda_j/\mu_{j,m_j}\). Con este cambio, (6.7.17) se convierte en

\[ \begin{align} p(\boldsymbol{m}) \quad &= \quad \prod^k_{i=1} p_i (m_i) \quad = \quad \prod^k_{i=1} p_i \ref{0} \prod^{m_i}_{j=0} \rho_{i,j} \\ p_i(0) \quad &= \quad \left[ 1+ \sum^{\infty}_{m=1} \prod^{m-1}_{j=0} \rho_{i,j} \right]^{-1} \end{align} \nonumber \]

Así,\(p(\boldsymbol{m})\) viene dada por la distribución del producto de los sistemas\(k\) individuales de nacimiento y muerte.

Redes Jackson cerradas

La segunda generalización es a una red de colas con un número fijo\(M\) de clientes en el sistema y sin entradas o salidas exógenas. Dichas redes se denominan redes Jackson cerradas, mientras que las redes analizadas anteriormente a menudo se denominan redes Jackson abiertas. Supongamos que una red cerrada de\(k\) nodo tiene probabilidades de enrutamiento\(Q_{ij} ,\, 1 \leq i, j \leq k\)\(\sum_j Q_{ij} = 1\), donde, y tiene tiempos de velocidad de servicio exponenciales\(μ_i\) (esto puede generalizarse\(μ_{i,m_i\) como arriba). Hacemos las mismas suposiciones que antes sobre la independencia de las variables de servicio y las variables de enrutamiento, y asumimos que hay una ruta entre cada par de nodos. Dado que\(\{ Q_{ij} ; 1 \leq i, j \leq k\}\) forma una matriz estocástica irreducible, existe un conjunto unidimensional de soluciones a las ecuaciones de estado estacionario

\[ \lambda_j = \sum_i \lambda_iQ_{ij}; \qquad 1\leq j \leq k \nonumber \]

Interpretamos\(\lambda_i \) como la tasa promedio de tiempo de las transiciones que van al nodo\(i\). Dado que este conjunto de ecuaciones solo puede resolverse dentro de una constante multiplicativa desconocida, y dado que esta constante solo puede determinarse al final del argumento, definimos\(\{\pi_i; 1 \leq i \leq k\}\) como la solución particular de (6.7.23) satisfactoria

\[ \pi_j = \sum_i \pi_i Q_{ij}; 1\leq j \leq k ; \sum_i \pi_i =1 \nonumber \]

Así, para todos\(i, \, \lambda_i= \alpha\pi_i\), donde\(\alpha\) hay alguna constante desconocida. El estado del proceso de Markov se toma nuevamente como\(\boldsymbol{m} = (m_1, m_2, . . . , m_k)\) con la condición\(\sum_i m_i = M\). Las tasas de transición del proceso de Markov son las mismas que para las redes abiertas, salvo que no hay llegadas o salidas exógenas; así (6.7.1) - (6.7.3) se sustituyen por

\[ q_{\boldsymbol{m,m'}} = \mu_i q_{ij} \quad \text{for } \boldsymbol{m'} = \boldsymbol{m} - \boldsymbol{e_i} + \boldsymbol{e_j}, \quad m_i>0, \, \, \, 1\leq i,j \leq k \nonumber \]

Nosotros planteamos la hipótesis de que el proceso de retroceso en el tiempo también es una red Jackson cerrada, y como antes, concluimos que si la hipótesis es cierta, las tasas de transición hacia atrás deberían ser

\[ \begin{align} q^*_{\boldsymbol{m,m'}} \quad &= \quad \mu_iQ^*_{ij} \quad \text{for } \boldsymbol{m'=m-e_i+e_j}, \, m_i>0, \, 1\leq i,j\leq k \\ \text{where } \lambda_iQ_{ij} \quad &= \quad \lambda_jQ^*_{ji} \quad \text{for } 1\leq i,j \leq k \end{align} \nonumber \]

Para volver a utilizar el Teorema 6.6.2, debemos verificar que\(p(\boldsymbol{m})\) existe un PMF satisfactorio\(p(\boldsymbol{m})q_{\boldsymbol{m,m'}} = p(\boldsymbol{m'})q^*_{\boldsymbol{m',m}}\) para todos los estados y transiciones posibles, y también debemos verificar eso\(\sum_{\boldsymbol{m'}} q_{\boldsymbol{m,m'}} = \sum_{\boldsymbol{m'}}q^*_{\boldsymbol{m,m'}}\) para todos los posibles\(\boldsymbol{m}\). Esta última verificación es prácticamente la misma que antes y se deja como ejercicio. La verificación anterior, con el uso de (72), (73) y (74), se convierte en

\[ p(\boldsymbol{m})(\mu_i/\lambda_i) = p(\boldsymbol{m'})(\mu_j)/\lambda_j) \quad \text{for } \boldsymbol{m'=m-e_i+e_j}, \quad m_i>0 \nonumber \]

Usando la solución de red abierta para guiar nuestra intuición, vemos que la siguiente elección de\(p(\boldsymbol{m})\) satisface (6.7.28) para todos los posibles\(\boldsymbol{m}\) (\(i.e.\), todos\(\boldsymbol{m}\) tales que\(\sum_i m_i = M \))

\[ p(\boldsymbol{m}) = A \prod^k_{i=1} (\lambda_i/\mu_i)^{m_i}; \quad \text{for }\boldsymbol{m}\text{ such that } \sum_i m_i =M \nonumber \]

La constante\(A\) es una constante normalizadora, elegida para hacer\(p(\boldsymbol{m})\) suma a la unidad. El problema con (6.7.29) es que no sabemos\(\lambda_i\) (excepto dentro de una constante multiplicativa independiente de\(i\)). Afortunadamente, sin embargo, si\(\pi_i/\alpha\)\(\lambda_i\) sustituimos vemos que\(\alpha\) se eleva al poder\(- M \), independiente del estado\(\boldsymbol{m}\). Así, dejando\(A'= A\alpha - M\), nuestra solución se convierte en

\[ \begin{align} p(\boldsymbol{m}) \quad &= \quad A'\prod^K_{i=1} ( \pi_i/\mu_i)^{m_i}: \,\,\, \text{for }\boldsymbol{m}\text{ such that } \sum_i m_i=M \\ \dfrac{1}{A'} \quad &= \quad \left. \sum_{\boldsymbol{m}: \sum_im_i=M} \prod^k_{i=1} \dfrac{\pi_i}{\mu_i} \right)^{m_i} \end{align} \nonumber \]

Tenga en cuenta que la distribución en estado estacionario de la red Jackson cerrada se ha encontrado sin resolver las tasas de transición promedio en el tiempo. Obsérvese también que la distribución en estado estacionario se ve muy similar a la de una red abierta; es decir, es una distribución de producto sobre los nodos con una distribución de tipo geométrico dentro de cada nodo. Esto es algo engañoso, sin embargo, ya que la constante\(A'\) puede ser bastante difícil de calcular. Es sorprendente al principio que el parámetro de la distribución geométrica se pueda cambiar por un multiplicador constante en (6.7.30) y (6.7.31) (\(i.e.\),\(\pi_i\) podría ser reemplazado por\(\lambda_i\)) y la solución no cambia; la cantidad importante son los valores relativos de\(\pi_i/μ_i\) desde un valor de \(i\)a otro más que al valor absoluto

Para encontrar\(\lambda_i\) (y esto es importante, ya que dice la rapidez con la que el sistema está haciendo su trabajo), tenga en cuenta que\(\lambda_i = \mu_i\text{Pr}\{m_i>0\}\). Resolver para\(\text{Pr}\{ m_i > 0\}\) requiere encontrar la constante\(A'\) en (6.7.25). De hecho, la mayor diferencia entre redes abiertas y cerradas es que las constantes relevantes para redes cerradas son tediosas de calcular (incluso por computadora) para redes grandes y grandes\(M \).