7.4: Probabilidades de cruce de umbrales en caminatas aleatorias

Sea {\(X_i; i \geq 1\)} una secuencia de variables aleatorias IID (rv), cada una con la función de distribución\(\mathsf{F}_X (x)\), y que {\(S_n; n \geq 1\)} sea una caminata aleatoria con\( S_n = X_1 +... + X_n\). Dejar\(g_X \ref{r} = \mathsf{E} [e^{rX} ]\) ser el MGF de\( X\) y dejar\(r_-\) y\( r_+\) ser los extremos superior e inferior del intervalo sobre el cual\(g(r)\) es finito. Asumimos a lo largo de eso\(r_− < 0 < r_+\). Cada uno de\(r_−\) y\(r_+\) podría estar contenido en el intervalo donde\(g_X (r)\) es finito, y cada uno de\( r_-\) y\(r_+\) podría ser infinito.

El objetivo principal de esta sección es desarrollar resultados sobre la probabilidad de que la secuencia {\(S_n; n \geq 1\)} alguna vez cruce un umbral dado\(\alpha > 0, \, i.e., \, \text{Pr}\{ \bigcup^{\infty}_{n=1} \{ S_n \geq α\alpha \}\} \). Asumimos a lo largo de esta sección que\(\overline{X} < 0\) y eso\(X\) toma valores tanto positivos como negativos con probabilidad positiva. Bajo estas condiciones, veremos que\(\text{Pr}\{\bigcup^{\infty}_{n=1}\{ S_n \geq \alpha \}\}\) está esencialmente delimitado por una función exponencialmente decreciente de\(\alpha\). En esta sección y en la siguiente, se evalúa este exponente y se muestra exponencialmente ajustado con el incremento\(\alpha \). La siguiente sección también encuentra un límite exponencialmente estrecho sobre la probabilidad de que\(\alpha \) se cruce un umbral at antes de que\(\beta < 0\) se cruce otro umbral at.

Chernoff Encuadernado

El límite de Chernoff se derivó y se discutió en la Sección 1.4.3. Se mostró en\ ref {1.62} que para cualquiera\(r \in (0, r_+)\) y cualquiera\( a > \overline{X}\), eso

\[ \text{Pr}\{ S_n \geq na\} \leq \exp (n[\gamma_X(r)-ra]) \nonumber \]

donde\(\gamma_X \ref{r} = \ln g_X (r)\) está el MGF semi-invariante de X. El límite más apretado de esta forma viene dado por

\[ \text{Pr}\{ S_n \geq na\} \leq \exp [ n\mu_X(a)] \qquad \text{where } \mu_X(a) = \inf_{r\in (0,r_+)} \gamma_X(r)-ra \nonumber \]

Esta optimización se ilustra en la Figura 7.6 para el caso en el\(\gamma_X (r)\) que es finita para todos los reales\(r\). La optimización se simplifica por el hecho (mostrado en el Ejercicio 1.24) que\(\gamma '' \ref{r} > 0\) para\(r \in (0, r_+)\). Lema 1.4.1 (que es casi obvio a partir de la figura) muestra que\(\mu_X \ref{a} < 0\) para\(a > \overline{X}\). Esto implica que para fijo\(a\), este límite disminuye exponencialmente en\(n\).

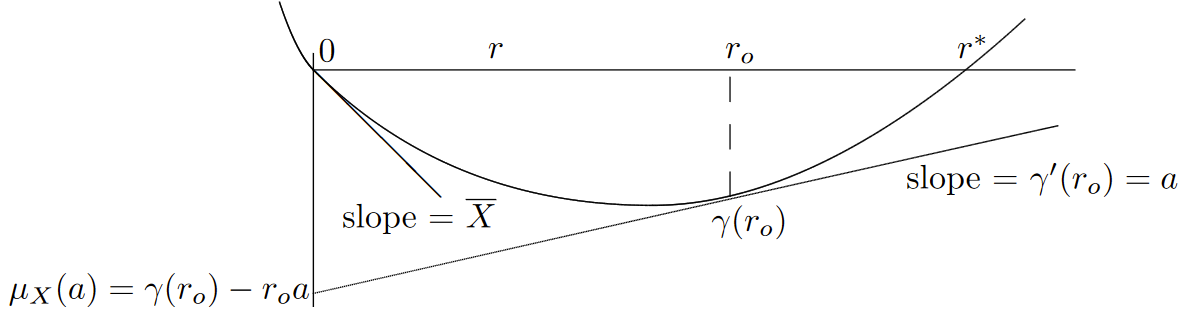
Figura 7.6: Minimización gráfica de\(\gamma(r) − ar\). Para cualquiera\(r, \, \gamma \ref{r} − ar\) es la intercepción del eje vertical de una línea de pendiente a a través del punto\( (r, \gamma (r))\). El mínimo ocurre cuando la línea de pendiente\(a\) es tangente a la curva,\(i.e.\), para la\( r\) tal que\(\gamma '(r) = a\).

Expresando la optimización en la figura algebraicamente, tratamos de minimizar\(\gamma \ref{r} − ar\) estableciendo el derivativo con respecto a\(r\) igual a 0. Asumiendo por el momento que esto tiene una solución y la solución es de algún valor\(r_o\), tenemos

\[ \text{Pr}\{ S_n \geq na \} \leq \exp \{ n [\gamma (r_o)-r_o\gamma '(r_o)]\} \qquad \text{where }\gamma '(r_o)=a \nonumber \]

Esto se puede expresar de manera algo más compacta sustituyendo\(\gamma '(r_o)\)\(a\) en el lado izquierdo de (7.. 4.2). Así, el atado de Chernoff dice que para cada uno\(r \in (0, r_+)\),

\[ \text{Pr} \{ S_n \geq n\gamma '(r) \} \leq \exp \{ n [ \gamma (r)-r\gamma ' (r)]\} \nonumber \]

En principio, ahora podríamos limitar la probabilidad de cruce de umbral,\(\text{Pr}\{\bigcup^{\infty}_{n=1}\{ S_n \geq \alpha \}\}\), usando la unión ligada sobre\(n\) y luego delimitando cada término por (7.4.2). Esto sería bastante tedioso y también nos daría poca idea. En cambio, hacemos una pausa para desarrollar el concepto de probabilidades inclinadas. Utilizaremos estas probabilidades inclinadas de tres maneras, primero para comprender mejor el encuadernado de Chernoff, segundo para demostrar que el encuadernado de Chernoff es exponencialmente apretado en el límite de grandes\(n\), y tercero para probar la identidad de Wald en la siguiente sección. La identidad de Wald, a su vez, proporcionará un límite superior en el\(\text{Pr}\{ \bigcup^{\infty}_{n=1}\{ S_n \geq \alpha \}\}\) que es esencialmente exponencialmente apretado en el límite de grandes\(\alpha \).

Probabilidades inclinadas

Como arriba, seamos {\(X_n; n \geq 1\)} una secuencia de IID rv y supongamos que\(g_X (r)\) es finito para\(r \in (r_−, r_+)\). Inicialmente se asume que\(X\) es discreto con el PMF\(\mathsf{p}_X (x)\) para cada valor\(x\) de muestra de\( X\). Para cualquier dado\( r \in (r_−, r_+)\), defina un nuevo PMF (llamado PMF inclinado) encendido\(X\) por

\[ \mathsf{q}_{X,r}(x)=\mathsf{p}_X(x)\exp [rx-\gamma (r)] \nonumber \]

Tenga en cuenta que\(\mathsf{q}_{X,r}(x) \geq 0\) para todos los valores de muestra\(x\) y\(\sum_x \mathsf{ q}_{X,r}(x) = \sum_x \mathsf{ p}_X \ref{x} e^{rx} /\mathsf{E} [e^{rx}] = 1,\) así esta es una asignación de probabilidad válida

Imagínese una caminata aleatoria, sumando IID rv\(X_i\), usando esta nueva asignación de probabilidad en lugar de la antigua. Luego tenemos el mismo mapeo desde puntos de muestra del espacio muestral subyacente hasta valores de muestra de rv, pero estamos tratando con un nuevo espacio de probabilidad\(i.e.\), hemos cambiado el modelo de probabilidad, y así hemos cambiado las probabilidades en la caminata aleatoria. Más adelante definiremos esta nueva medida de probabilidad para que los rv\(X_1, X_2, . . .\) en este nuevo espacio de probabilidad sean IID. ¹ Por cada evento en el antiguo paseo, el mismo evento existe en el nuevo paseo, pero su probabilidad ha cambiado.

Usando (7.4.4), junto con la suposición de que\(X_1, X_2, . . .\) son independientes en la asignación de probabilidad inclinada, el PMF inclinado de una\(n\) tupla\(\boldsymbol{X} = (X_1, X_2, . . . , X_n)\) viene dado por

\[\mathsf{q}_{\boldsymbol{X}^n,r}(x_1,...,x_n) = \mathsf{p}_{\boldsymbol{X}^n}(x_1,...,x_n) \exp ( \sum_{i=1}^n [rx_i-\gamma (r)] \nonumber \]

A continuación debemos relacionar el PMF de la suma,\(\sum_{i=1}^n X_i\), en la medida de probabilidad original con el de la medida de probabilidad inclinada. De (7.4.5), tenga en cuenta que por cada\(n\) -tupla\((x_1, . . . , x_n)\) para la cual\(\sum^n_{i=1} x_i = s_n\) (para cualquier dado\( s_n\)) tenemos

\[ \mathsf{q}_{\boldsymbol{X}^n,r}(x_1,...,x_n) = \mathsf{p}_{\boldsymbol{X}^n}(x_1,...,x_n) \exp [rs_n -n\gamma (r)]\nonumber \]

Sumando sobre todo\( \boldsymbol{x}^n\) para lo cual\(\sum^n_{i=1} x_i = s_n\), luego obtenemos una relación notable entre el PMF para\( S_n\) en el original y las medidas de probabilidad inclinadas:

\[ \mathsf{q}_{\boldsymbol{S}_n,r}(s_n) = \mathsf{p}_{S_n}(s_n)\exp [rs_n-n\gamma (r)] \nonumber \]

Esta ecuación es la clave de la teoría de grandes desviaciones aplicada a las sumas de IID rv. La medida inclinada de\( S_n\), para positivo\( r\), aumenta la probabilidad de valores grandes\(S_n\) y disminuye la de valores pequeños. Dado que\(S_n\) es una suma IID bajo la medida inclinada, sin embargo, podemos usar las leyes de números grandes y el CLT alrededor de la media inclinada para obtener buenas estimaciones y límites sobre el comportamiento de\(S_n\) lejos de la media para la medida original.

Ahora denotamos la media de\( X\) en la medida inclinada como\(\mathsf{E}_r[X]\). Usando (7.4.4),

\[ \begin{align} \mathsf{E}_r[X] \quad &= \quad \sum_x x\mathsf{q}_{X,r}(x) = \sum_x \mathsf{p}_X(x) \exp [rx-\gamma \ref{r} ] \nonumber \\ &= \quad \dfrac{1}{g_X(r)} \sum_x \dfrac {d}{dr} \mathsf{p}_X(x) \exp [rx] \nonumber \\ &= \quad \dfrac{g'_X(r)}{g_X(r)} = \gamma' \ref{r} \end{align} \nonumber \]

Momentos superiores de\(X\) bajo la medida inclinada se pueden calcular de la misma manera, pero, de manera más elegante, se puede ver que el MGF de\( X\) debajo de la medida inclinada es\(\mathsf{E}_r[\exp (tX)] = g_X (t + r)/g_X (r)\).

El siguiente teorema utiliza (7.4.6) y (7.4.7) para mostrar que el límite de Chernoff es exponencialmente apretado.

Teorema 7.4.1. Sea {\(X_n; n \geq 1\)} una secuencia IID discreta con un MGF finito para\(r \in (r_−, r_+)\) donde\( r_− < 0 < r_+\). Dejar\( S_n = \sum^n_{i=1}x_i\) para cada uno\(n ≥ 1\). Entonces para cualquiera\( r \in (0, r_+)\), y cualquiera\( \epsilon > 0\) y\(\delta > 0\) hay una m tal que para todos\(n ≥ m\),

\[ \text{Pr}\{S_n \geq n(\gamma' \ref{r} - \in) \} \quad \geq \quad (1-\delta) \exp [n(\gamma (r)-r\gamma' \ref{r} - r\epsilon )] \nonumber \]

Prueba: La débil ley de los grandes números, en la forma de (1.76), se aplica a la medida inclinada en cada uno\( S_n\). Escribiendo el límite\( n\) ahí, vemos que para cualquiera\(\epsilon , \delta \), hay\( m\) tal que para todos\(n \geq m\),

\[ \begin{align} 1-\delta \quad &\leq \sum_{(\gamma'(r)-\epsilon )n \leq s_n \leq (\gamma' (r)+\epsilon )n} \mathsf{q}_{S_n,r} (s_n) \nonumber \\ &= \sum_{(\gamma'(r)-\epsilon )n \leq s_n \leq (\gamma' (r)+\epsilon )n} \mathsf{p}_{S_n}(s_n)\exp [rs_n - n \gamma \ref{r} ] \\ &\leq \sum_{(\gamma'(r)-\epsilon )n \leq s_n \leq (\gamma' (r)+\epsilon )n} \mathsf{p}_{S_n}(s_n)\exp [n(r\gamma' \ref{r} +r\epsilon - \gamma (r))] \\ &\leq \sum_{(\gamma' (r)-\epsilon )n \leq s_n} \mathsf{p}_{S_n}(s_n)\exp [ n(r\gamma' \ref{r} + r\epsilon - \gamma (r))] \\ &= \exp [n(r\gamma' \ref{r} + r\epsilon - \gamma (r))] \text{Pr} \{ S_n \geq n (\gamma' \ref{r} - \epsilon ) \} \end{align} \nonumber \]

La igualdad (7.4.9) se desprende de (7.4.6) y la desigualdad (7.4.10) sigue porque\(s_n \leq \gamma' \ref{r} + \epsilon \) en la suma. La siguiente desigualdad es el resultado de agregar términos positivos adicionales a la suma, y (7.4.12) simplemente reemplaza la suma sobre un PMF con la probabilidad del evento dado. Dado que (7.4.12) equivale a (7.4.8), la prueba está completa.

\( \square \)

La estructura de la prueba anterior se puede utilizar en muchas situaciones. Se utiliza una medida de probabilidad inclinada para enfocarse en la cola de una distribución, y luego se usa algún resultado conocido sobre la distribución inclinada para derivar el resultado deseado sobre la distribución dada.

Volver a cruces de umbral

El límite de Chernoff es conveniente (y exponencialmente apretado) para entender\(\text{Pr}\{ S_n \geq na\} \) como una función de\(n\) para fijo\(a\). No nos da tanto conocimiento directo\(\text{Pr}\{ S_n \geq α \}\) como una función de\(n\) para fijo\(\alpha \), lo que nos dice algo sobre cuándo\(\alpha \) es más probable que se cruce un umbral at. Se puede lograr una visión adicional sustituyendo\( \alpha /\gamma' (r_0)\)\(n\) en (7.4.2), obteniendo

\[ \text{Pr} \{S_n \geq \alpha \} \leq \exp \left\{ \alpha \left[ \dfrac{\gamma (r_o)}{\gamma' (r_o) } -r_o \right] \right\} \qquad \text{where } \gamma' (r_o) = \alpha /n \nonumber \]

Una bonita interpretación gráfica de esta ecuación se da en la Figura 7.7. Obsérvese que el exponente en\(\alpha \),\(\gamma (r_0)/ \gamma' (r_0) − r_0\) es decir, es el negativo de la intercepción del eje horizontal de la línea de pendiente\(\gamma' (r_0) = \alpha /n\) en la Figura 7.7.

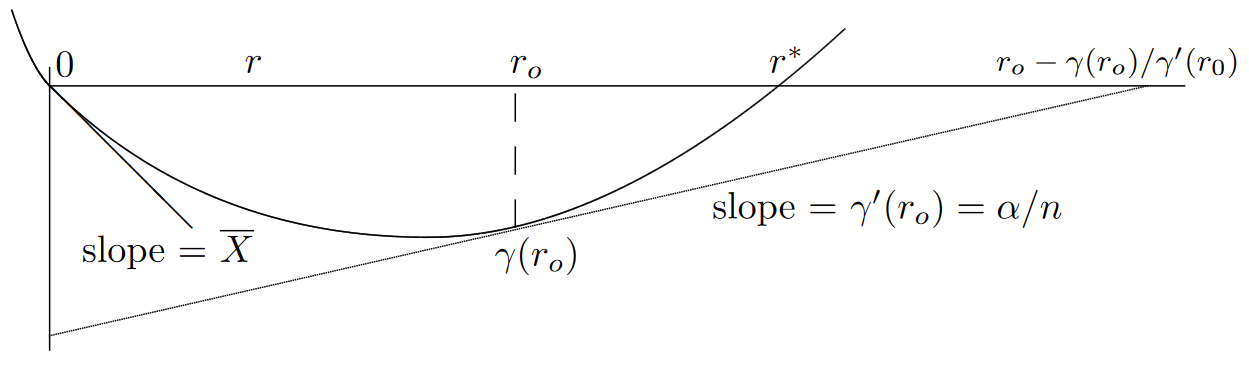
Figura 7.7: El exponente en\(\alpha \) for\(\text{Pr}\{ S_n \geq \alpha \}\), minimizado sobre r. La minimización es la misma que la de la Figura 7.6, pero\(\gamma (r_o)/ \gamma' (r_o) − r_o\) es el negativo de la intercepción del eje horizontal de la línea tangente a\(\gamma (r)\) at\(r = r_0\)

Para fijo\(\alpha \), entonces, vemos que para muy grandes\(n\), la pendiente\(\alpha /n\) es muy pequeña y esta intercepción horizontal es muy grande. A medida\(n\) que disminuye, la pendiente\(r_0\) aumenta, aumenta y disminuye la intercepción horizontal. Cuando\( r_0\) aumenta hasta el punto etiquetado\( r^*\) en la figura, es decir, el\(r > 0\) en el que\(\gamma \ref{r} = 0\), entonces el exponente disminuye a\(r^*\). Cuando\(n\) disminuye aún más,\(r_0\) se vuelve más grande que\(r^*\) y la intercepción horizontal comienza a aumentar nuevamente.

Dado que\(r^∗\) es la intercepción mínima del eje horizontal de esta clase de líneas rectas, vemos que la siguiente encuadernación sostiene para todos\( n\),

\[ \text{Pr} \{ S_n \geq \alpha \} \leq \exp (-r^* \alpha ) \qquad \text{for arbitrary } \alpha > 0,n\geq 1 \nonumber \]

donde\(r^*\) está la raíz positiva de\(\gamma \ref{r} = 0\).

El argumento gráfico anterior asumió que hay algunos\(r^* > 0\) tales que\(\gamma_X (r^*) = 0\). Sin embargo\( r_+ = \infty \), si, entonces (ya que\(X\) toma valores positivos con probabilidad positiva por suposición)\(\gamma (r)\) puede verse acercarse\(\infty \) como\(r \rightarrow \infty\). Así\(r^*\) debe existir por la continuidad de\(\gamma (r)\) in\((r_−, r_+)\). Esto se resume en el siguiente lema.

Lema 7.4.1. Sea {\( S_n = X_1 + ...+ X_n; n \geq 1\)} un paseo aleatorio donde {\(X_i; i \geq 1\)} es una secuencia IID donde\( g_X (r)\) existe para todos\(r \geq 0\)\(\overline{X} < 0\), dónde y dónde\(X\) toma valores positivos y negativos con probabilidad positiva. Entonces para todos los enteros\(n > 0\) y todos\(\alpha > 0\)

\[ \text{Pr}\{ S_n \geq \alpha \} \leq \exp \{ \alpha [\gamma (r_0)n/\alpha -r_0] \} \leq \exp (-r^*\alpha ) \nonumber \]

donde\(\gamma' (r_o) = \alpha /n\).

A continuación consideramos brevemente la situación donde\(r_+ < \infty\). Hay dos casos a considerar, primero donde\(\gamma (r_+)\) es infinito y segundo donde es finito. Ejemplos de estos casos se dan en el Ejercicio 1.22, partes b) y c) respectivamente. Para el caso\(\gamma (r_+) = \infty \), el Ejercicio 1.23 muestra que\(\gamma (r)\) va a\(\infty \) como\(r\) aumenta hacia\(r_+\). Así\(r^*\) debe existir en este caso 1 por continuidad.

El caso\(\gamma (r_+) < \infty \) se explica mejor por la Figura 7.8. Como ahí se explicó, si\(\gamma' \ref{r} = \alpha /n\) para algunos\( r_0 < r_+\), entonces (7.4.2) y (7.4.13) se mantienen como antes. Alternativamente, si es\(\alpha /n > \gamma' (r)\) para todos\(r < r_+\), entonces el límite de Chernoff está optimizado en\( r = r_+\), y tenemos

\[ \text{Pr} \{S_n \geq \alpha \} \leq \exp \{ n[\gamma (r_+)-r_+\alpha /n] \} = \exp \{ \alpha [\gamma (r_+)n/\alpha -r_+]\} \nonumber \]

Si modificamos la definición de\(r^*\) ser el supremo de\( r > 0\) tal que\(\gamma \ref{r} < 0\), entonces\(r^* = r_+\) en este caso, y (7.4.15) es válido en general con la obvia modificación de\(r_o\).

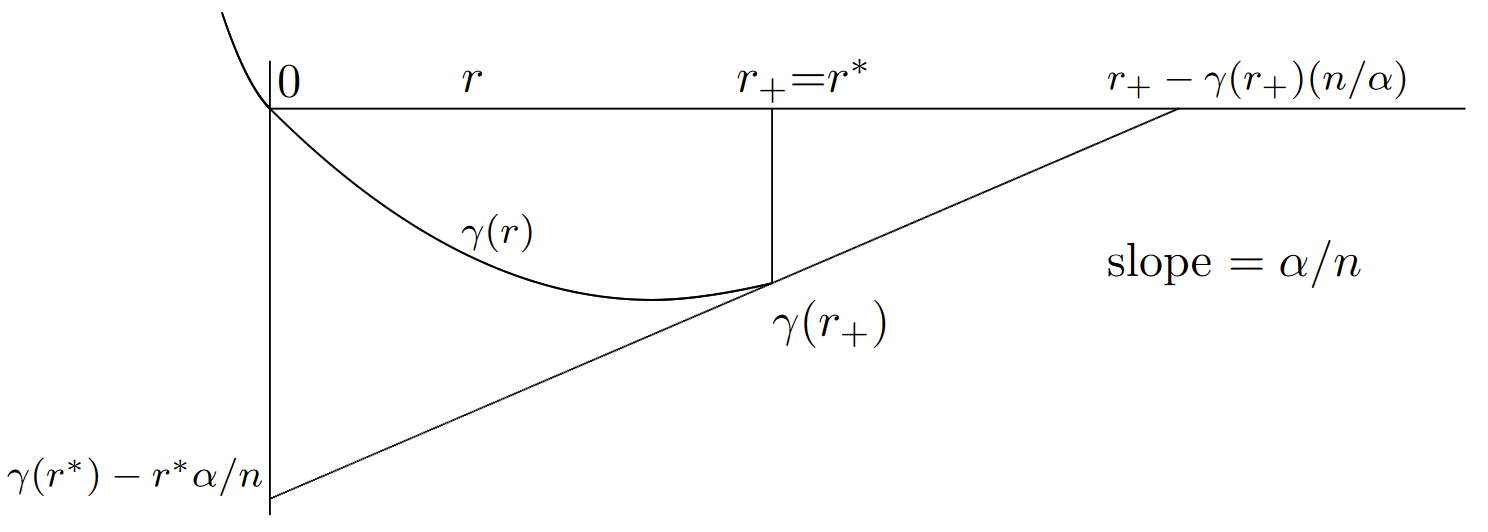
Figura 7.8: Minimización gráfica de\(\gamma \ref{r} − (\alpha /n)r\) para el caso donde\(\gamma (r^+) < \infty\). Como antes, para cualquier\(r < r_+\), podemos encontrar\(\gamma (r)−r\alpha /n\) dibujando una línea de pendiente\((\alpha /n)\) desde el punto\((r, \gamma (r))\) hasta el eje vertical. Si\(\gamma' \ref{r} = \alpha /n\) para algunos\( r < r_+\), el mínimo ocurre a eso\( r\). De lo contrario, como se muestra en la figura, ocurre en\(r = r_+\).

Ahora podríamos usar este resultado, más el límite de unión, para encontrar un límite superior sobre la probabilidad de cruce de umbral,\(i.e.\),\(\text{Pr}\{\bigcup^{\infty}_{n=1} \{S_n \geq \alpha \}\}\). Los coeficientes en esto son algo desordenados y cambian según los casos especiales discutidos anteriormente. Es mucho más instructivo y elegante desarrollar la identidad de Wald, lo que demuestra que\(\text{Pr}\{ \bigcup_n \{ S_n \geq \alpha \}\} \leq \exp [−\alpha r^*]\). Esto es un poco más fuerte que el enfoque de Chernoff ligado en el sentido de que el límite sobre la probabilidad de la unión es el mismo que en un solo término en el enfoque de Chernoff ligado. El principal valor del enfoque de Chernoff, entonces, es proporcionar la seguridad de que el encuadernado es exponencialmente apretado.

______________________________________

1. Uno podría preguntarse si\(X_1, X_2, . . .\) son las mismas rv en esta nueva medida de probabilidad que en la antigua. Por lo general, es conveniente verlas como iguales, ya que corresponden al mismo mapeo desde puntos de muestreo hasta valores de muestra en ambas medidas de probabilidad. Sin embargo, dado que el espacio de probabilidad ha cambiado, se pueden ver igualmente bien como diferentes rv. No hace ninguna diferencia qué punto de vista se adopta, ya que todos usamos la relación en (7.4.4), y otras relaciones similares, para calcular probabilidades en el sistema original.