7.7: Submartingales y Supermartingales

Las submartingales y las supermartingales son generalizaciones simples de martingales que proporcionan muchos resultados útiles para muy poco trabajo adicional. Posteriormente derivaremos la desigualdad de la submartingala de Kolmogorov, que es una generalización poderosa de la desigualdad de Markov. Usamos esto tanto para dar una prueba simple de la fuerte ley de los grandes números como también para comprender mejor los problemas de cruce de umbrales para caminatas aleatorias.

Definición 7.7.1. Una submartingala es un proceso estocástico de tiempo entero {\(Z_n; n ≥ 1\)} que satisface las relaciones

\[ \mathsf{E} [|Z_n|]<\infty \quad ; \quad \mathsf{E}[Z_n|Z_{n-1},Z_{n-2},...,Z_1] \geq Z_{n-1} \quad ; \quad n \geq 1 \nonumber \]

Una supermartingala es un proceso estocástico de tiempo entero {\(Z_n; n ≥ 1\)} que satisface las relaciones

\[ \mathsf{E}[|Z_n|] <\infty \quad ; \quad \mathsf{E}[Z_n|Z_{n-1},Z_{n-1},...,Z_1]\leq Z_{n-1} \quad ; \quad n \geq 1 \nonumber \]

En términos de nuestra analogía de juego, una submartingala corresponde a un juego que es al menos justo\(i.e.\),, donde la fortuna esperada del jugador o aumenta o sigue siendo la misma. Una supermartingala es un proceso con el tipo opuesto de desigualdad. ¹

Dado que una martingala satisface tanto (7.7.1) como (7.7.2) con igualdad, una martingala es a la vez una submartingala y una supermartingala. Tenga en cuenta que si {\(Z_n; n ≥ 1\)} es una submartingala, entonces {\(−Z_n; n ≥ 1\)} es una supermartingala, y a la inversa. De esta manera, algunos de los resultados a seguir se exponen únicamente para las submartingales, entendiendo que pueden aplicarse a las supermartingales cambiando los signos como arriba.

Lema 7.6.1, con la igualdad reemplazada por desigualdad, también se aplica a las submartingales y supermartingales. Es decir, si {\(Z_n; n ≥ 1\)} es una submartingala, entonces

\[ \mathsf{E}[Z_n|Z_i,Z_{i-1},...,Z_1] \geq Z_i \quad ; \quad 1\leq i<n \nonumber \]

y si {\(Z_n; n ≥ 1\)} es una supermartingala, entonces

\[ \mathsf{E}[Z_n|Z_i,Z_{i-1},...,Z_1] \leq Z_i \quad ; \quad 1 \leq i<n \nonumber \]

Las ecuaciones (7.7.3) y (7.7.4) se verifican de la misma manera que Lemma 7.6.1 (ver Ejercicio 7.18). De igual manera, la generalización apropiada de (7.6.13) es que si {\(Z_n; n ≥ 1\)} es una submartingala, entonces

\[ \mathsf{E}[Z_n] \geq \mathsf{E}[Z_i] \quad ; \quad \text{for all } i, \, 1\leq i <n \nonumber \]

y si {\(Z_n; n ≥ 1\)} es una supermartingala, entonces

\[ \mathsf{E}[Z_n] \leq \mathsf{E}[Z_i] \quad ; \quad \text{for all } i, \, 1 \leq i<n \nonumber \]

Una caminata aleatoria {\(S_n; n ≥ 1\)} con\(S_n = X_1 +... + X_n\) es una submartingala, martingala, o supermartingala respectivamente para\(\overline{X} ≥ 0, \overline{X} = 0\), o\(\overline{X} ≤ 0\). Además, si\(X\) tiene una función de generación de momento semi-invariante\(\gamma (r)\) para algunos dados\(r\), y si\(Z_n\) se define como\(Z_n = \exp (rS_n)\), entonces el proceso {\(Z_n; n ≥ 1\)} es una submartingala, martingala o supermartingala respectivamente para\(\gamma \ref{r} ≥ 0,\, \gamma \ref{r} = 0\), o\( \gamma \ref{r} ≤ 0\). El siguiente ejemplo da una manera importante en la que se relacionan martingales y submartingales.

Ejemplo 7.7.1 (Funciones convexas de martingales) La figura 7.11 ilustra la gráfica de una función convexa\(h\) de una variable real\(x\). Una función\(h\) de una variable real se define como convexa si, para cada punto\(x_1\), hay un número real\(c\) con la propiedad que\(h(x_1) + c(x − x_1) ≤ h(x)\) para todos\(x\)

Geométricamente, esto dice que cada tangente a\( h(x)\) yace sobre o por debajo\(h(x)\). Si\( h(x)\) tiene una derivada en\(x_1\), entonces\(c\) es el valor de esa derivada y\(h(x_1) + c(x − x_1)\) es la línea tangente at\(x_1\). Si\(h(x)\) tiene una pendiente discontinua en\(x_1\), entonces podría haber muchas opciones para\(c\); por ejemplo,\(h(x) = |x|\) es convexa, y para\(x_1 = 0\), se podría elegir cualquiera\(c\) en el rango −1 a +1.

Una condición simple que implica convexidad es una segunda derivada no negativa en todas partes. Esto no es necesario, sin embargo, y las funciones pueden ser convexas incluso cuando la primera derivada no existe en todas partes. Por ejemplo, la función\(\gamma (r)\) en la Figura 7.8 es convexa a pesar de que es finita\(r = r_+\) e infinita para todos\(r > r_+\).

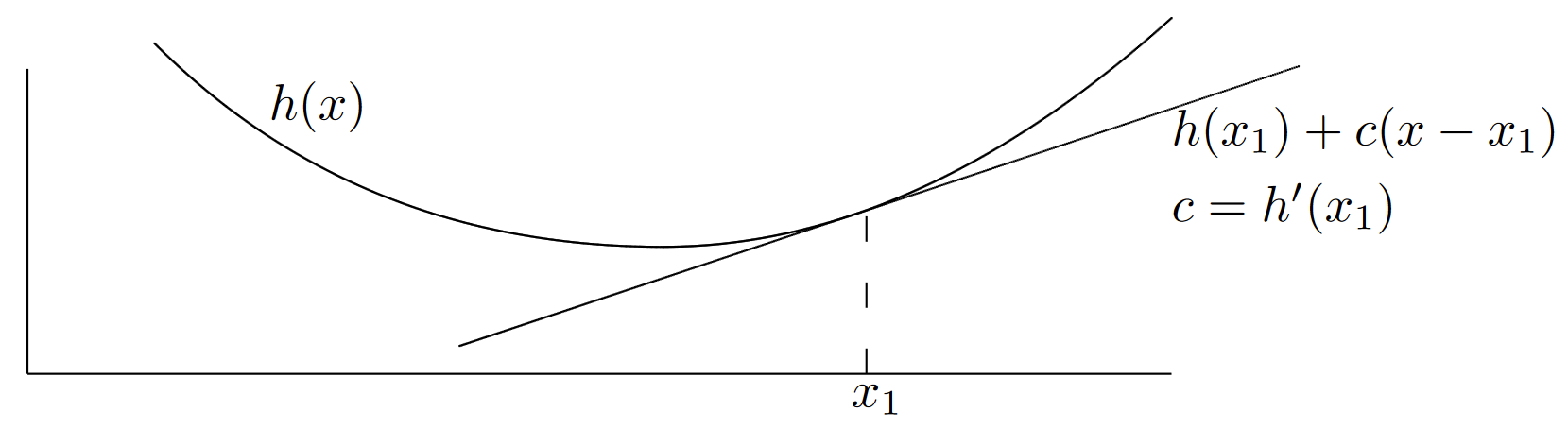
Figura 7.11: Funciones convexas: Para cada uno\(x_1\), hay un valor de\(c\) tal que, para todos\(x\),\(h(x_1) + c(x − x_1) ≤ h(x)\). Si\(h\) es diferenciable en\(x_1\), entonces\(c\) es la derivada de\(h\) at\(x_1\)

La desigualdad de Jensen afirma que si\(h\) es convexa y\(X\) es una variable aleatoria con expectativa, entonces\(h(\mathsf{E} [X]) ≤ \mathsf{E} [h(X)]\). Para probarlo, vamos\(x_1 = \mathsf{E} [X]\) y elijan\(c\) para que\(h(x_1) + c(x − x_1) ≤ h(x)\). Usando la variable aleatoria\(X\) en lugar de\(x\) y tomando los valores esperados de ambos lados, obtenemos la desigualdad de Jensen. Obsérvese que para cualquier evento en particular\(A\), este mismo argumento se aplica a\(X\) condicional\(A\), de manera que eso\(h(\mathsf{E} [X | A]) ≤ \mathsf{E} [h(X) | A]\). La desigualdad de Jensen es muy utilizada; es un milagro menor que no la hayamos requerido previamente.

Teorema 7.7.1. Supongamos que\(h\) es una función convexa de una variable real, que {\(Z_n; n ≥ 1\)} es una martingala o submartingala, y eso\(\mathsf{E} [|h(Z_n)|] < \infty \) para todos\(n\). Entonces {\(h(Z_n); n ≥ 1\)} es una submartingala.

Prueba: Para cualquier elección de\(z_1, . . . , z_{n−1}\), podemos usar la desigualdad de Jensen con las probabilidades de condicionamiento para obtener

\[\mathsf{E}[h(Z_n)|Z_{n-1}=z_{n-1},...,Z_1=z_1] \geq h(\mathsf{E}[Z_n|Z_{n-1}=z_{n-1},...,Z_1=z_1])=h(z_{n-1}) \nonumber \]

Para cualquier elección de números\(h_1, . . . , h_{n−1}\) en el rango de la función\(h\), deja\(z_1, . . . , z_{n−1}\) ser números arbitrarios satisfactorios\(h(z_1)=h_1, . . . , h(z_{n−1})=h_{n−1}\). Para cada una de esas opciones, (7.7.7) sostiene, de manera que

\[ \begin{align} \mathsf{E}[h(Z_n)|h(Z_{n-1})=h_{n-1},...,h(Z_1)=h_1] \quad &\geq \quad h(\mathsf{E}[Z_n|h(Z_{n-1})=h_{n-1},...,h(Z_1)=h_1]) \nonumber \\ &= \quad h(z_{n-1}) = h_{n-1} \end{align} \nonumber \]

cumplimentando la prueba.

\( \square \)

Algunos ejemplos de este resultado, aplicado a una martingala {\(Z_n; n ≥ 1\)}, son los siguientes:

\[ \begin{align} &\{ |Z_n|;\, n\geq \} \text{ is a submartingale} \\ &\{ Z_n^2; \, n\geq 1\} \text{ is a submartingale if } \mathsf{E}[Z_n^2]<\infty \\ &\{\exp (rZ_n); \, n\geq 1\} \text{ is a submartingale for } r \text{ such that } \mathsf{E}[\exp (rZ_n)]<\infty \end{align} \nonumber \]

Una función de una variable real\(h(x)\) se define como cóncava si\(−h(x)\) es convexa. Se deduce entonces del Teorema 7.7.1 que si\(h\) es cóncava y {\(Z_n; n ≥ 1\)} es una martingala, entonces {\(h(Z_n); n ≥ 1\)} es una supermartingala (asumiendo que\(\mathsf{E} [|h(Z_n)|] < \infty \)). Por ejemplo, si {\(Z_n; n ≥ 1\)} es una martingala positiva y\(\mathsf{E} [| \ln (Z_n)|] < \infty \), entonces {\(\ln (Z_n); n ≥ 1\)} es una supermartingala.

_______________________________________

1. La forma más fácil de recordar la diferencia entre una submartingala y una supermartingala es recordar que es contraria a lo que dictaría el sentido común.