3.1: Sistemas de Tiempo Continuos
- Page ID
- 86295
Introducción
Como ya sabe ahora, un sistema de tiempo continuo opera en una entrada de señal de tiempo continua y produce una salida de señal de tiempo continua. Existen numerosos ejemplos de sistemas de tiempo continuo útiles en el procesamiento de señales, ya que esencialmente describen el mundo que nos rodea. La clase de sistemas de tiempo continuo que son lineales e invariantes en el tiempo, conocidos como sistemas LTI de tiempo continuo, es de particular interés ya que las propiedades de linealidad e invarianza de tiempo juntas permiten el uso de algunas de las herramientas más importantes y poderosas en el procesamiento de señales.
Sistemas de Tiempo Continuos
Linealidad e Invarianza de Tiempo
\(H\)Se dice que un sistema es lineal si satisface dos condiciones importantes. El primero, aditividad, afirma por cada par de señales\(x\),\(y\) eso\(H(x+y)=H(x)+H(y)\). El segundo, la homogeneidad del grado uno, establece por cada señal\(x\) y escalar\(a\) que tenemos\(H(ax)=aH(x)\). Es claro que estas condiciones se pueden combinar juntas en una sola condición para la linealidad. Así, se dice que un sistema es lineal si por cada señal\(x\),\(y\) y escalares\(a\),\(b\) tenemos eso
\[H(a x+b y)=a H(x)+b H(y) \nonumber \]
La linealidad es una propiedad particularmente importante de los sistemas, ya que nos permite aprovechar las poderosas herramientas del álgebra lineal, como bases, vectores propios y valores propios, en su estudio.
Se dice que un sistema\(H\) es invariable en el tiempo si un desplazamiento de tiempo de una entrada produce la salida desplazada correspondiente. En otras palabras, más precisas, el sistema\(H\) viaja con el operador de turno de tiempo\(S_T\) para cada\(T \in \mathbb{R}\). Es decir,
\[S_{T} H=H S_{T} \nonumber \]
La invarianza temporal es deseable porque facilita la computación mientras refleja nuestra intuición de que, de todos modos iguales, los sistemas físicos deben reaccionar igual a entradas idénticas en diferentes momentos.
Cuando un sistema exhibe ambas propiedades importantes, permite un análisis más straigtforward de lo que sería posible de otra manera. Como se explicará y probará en módulos posteriores, el cálculo de la salida del sistema para una entrada dada se convierte en una simple cuestión de convolucionar la entrada con la señal de respuesta al impulso del sistema. También se demostró posteriormente, el hecho de que los exponenciales complejos son vectores propios de sistemas lineales invariantes en el tiempo permitirá el uso de herramientas de dominio de frecuencia como las diversas transformaciones de Fourier y funciones de transferencia asociadas, para describir el comportamiento de los sistemas lineales invariantes en el tiempo.
Ejemplo\(\PageIndex{1}\)
Considera el sistema\(H\) en el que
\[H(f(t))=2 f(t) \nonumber \]
para todas las señales\(f\). Dadas dos señales cualesquiera\(f\),\(g\) y escalares\(a\),\(b\)
\[H(a f(t)+b g(t)))=2(a f(t)+b g(t))=a 2 f(t)+b 2 g(t)=a H(f(t))+b H(g(t)) \nonumber \]
para todos los reales\(t\). Así,\(H\) es un sistema lineal. Para todos los reales\(T\) y señales\(f\),
\[S_{T}(H(f(t)))=S_{T}(2 f(t))=2 f(t-T)=H(f(t-T))=H\left(S_{T}(f(t))\right) \nonumber \]
para todos los reales\(t\). Así,\(H\) es un sistema invariante en el tiempo. Por lo tanto,\(H\) es un sistema lineal invariante en el tiempo.
Representación de ecuaciones diferenciales
A menudo es útil describir sistemas usando ecuaciones que involucran la tasa de cambio en alguna cantidad. Para los sistemas de tiempo continuo, tales ecuaciones se denominan ecuaciones diferenciales. Una clase importante de ecuaciones diferenciales es el conjunto de ecuaciones diferenciales ordinarias de coeficiente constante lineal, que se describen con más detalle en módulos posteriores.
Ejemplo\(\PageIndex{2}\)
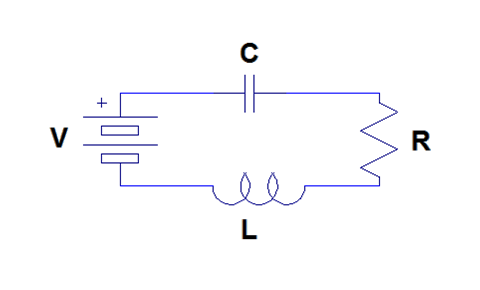
Considere el circuito RLC en serie que se muestra en la Figura\(\PageIndex{1}\). Este sistema se puede modelar usando ecuaciones diferenciales. Podemos usar las ecuaciones de voltaje para cada elemento del circuito y la ley de voltaje de Kirchoff para escribir una ecuación diferencial de coeficiente constante lineal de segundo orden que describa la carga en el condensador.
El voltaje a través de la batería es simplemente\(V\). El voltaje a través del condensador es\(\frac{1}{C}q\). El voltaje a través de la resistencia es\(R\frac{dq}{dt}\). Finalmente, el voltaje a través del inductor es\(L \frac{d^{2} q}{d t^{2}}\). Por lo tanto, por la ley de tensión de Kirchoff, se deduce que
\[L \frac{d^{2} q}{d t^{2}}+R \frac{d q}{d t}+\frac{1}{C} q=V \nonumber \]
Resumen de Sistemas de Tiempo Continuos
Muchos sistemas de tiempo continuo útiles se encontrarán en un estudio de señales y sistemas. Este curso está más interesado en aquellos que demuestran tanto la propiedad de linealidad como la propiedad de invarianza de tiempo, que en conjunto permiten el uso de algunas de las herramientas más potentes del procesamiento de señales. A menudo es útil describirlos en términos de tasas de cambio a través de ecuaciones diferenciales ordinarias de coeficiente constante lineal.


