3.7: Ecuaciones diferenciales de coeficiente constante lineal

Introducción: Ecuaciones Diferenciales Ordinarias

En nuestro estudio de señales y sistemas, a menudo será útil describir sistemas usando ecuaciones que involucran la tasa de cambio en alguna cantidad. Tales ecuaciones se denominan ecuaciones diferenciales. Por ejemplo, tal vez recuerdes de un curso de física pasado que un objeto experimenta un movimiento armónico simple cuando tiene una aceleración que es proporcional a la magnitud de su desplazamiento y opuesta en dirección. Así, este sistema se describe como la ecuación diferencial mostrada en la Ecuación\ ref {3.58}.

\[\frac{d^{2} x}{d t^{2}}=-c x \label{3.58} \]

Debido a que la ecuación diferencial en la Ecuación\ ref {3.58} tiene solo una variable independiente y solo tiene derivadas con respecto a esa variable, se denomina ecuación diferencial ordinaria. Existen ecuaciones diferenciales más complicadas, como la ecuación de Schrödinger, que involucra derivadas con respecto a múltiples variables independientes. Estas se denominan ecuaciones diferenciales parciales, pero no están dentro del alcance de este módulo.

Dado un conjunto suficientemente descriptivo de condiciones iniciales o condiciones de límite, si hay una solución a la ecuación diferencial, esa solución es única y describe el comportamiento del sistema. Por supuesto, los resultados sólo son precisos en la medida en que el modelo refleja la realidad.

Coeficiente constante lineal Ecuaciones diferenciales ordinarias

Una subclase importante de ecuaciones diferenciales ordinarias es el conjunto de ecuaciones diferenciales ordinarias de coeficiente constante lineal. Estas ecuaciones son de la forma

\[A x(t)=f(t) \label{3.59} \]

donde\(A\) es un operador diferencial de la forma dada en la Ecuación\ ref {3.60}.

\[A=a_{n} \frac{d^{n}}{d t^{n}}+a_{n-1} \frac{d^{n-1}}{d t^{n-1}}+\ldots+a_{1} \frac{d}{d t}+a_{0} \label{3.60} \]

Tenga en cuenta que los operadores de este tipo satisfacen las condiciones de linealidad, y\(a_1,...,a_n\) son constantes reales. Además, la Ecuación\ ref {3.59} con estos operadores tiene derivadas con respecto a una sola variable, convirtiéndola en una ecuación diferencial ordinaria.

Un concepto similar para un ajuste de tiempo discreto, ecuaciones de diferencia, se discute en el capítulo sobre análisis de dominio de tiempo de sistemas discretos de tiempo. Hay muchos paralelismos entre la discusión de ecuaciones diferenciales ordinarias de coeficiente constante lineal y ecuaciones de diferencia de coeficientes constantes lineales.

Aplicaciones de Ecuaciones Diferenciales

Considere el modelo de desintegración en el que una cantidad de isótopo inestable disminuye a una velocidad proporcional a la cantidad de isótopo inestable restante. Así, la desintegración del isótopo es modelada por la ecuación diferencial de coeficiente constante lineal de primer orden

\[\frac{d x}{d t}+r x=0 \nonumber \]

donde\(r\) hay alguna tasa real.

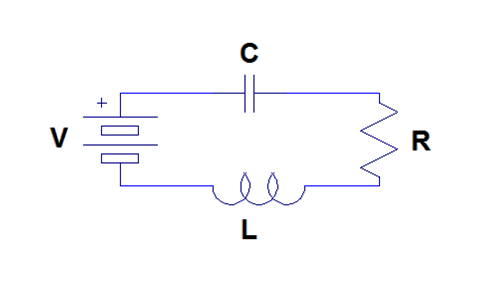
Ahora considere el circuito RLC en serie que se muestra en la Figura\(\PageIndex{1}\). Este sistema se puede modelar usando ecuaciones diferenciales. Podemos usar las ecuaciones de voltaje para cada elemento del circuito y la ley de voltaje de Kirchoff para escribir una ecuación diferencial de coeficiente constante lineal de segundo orden que describa la carga en el condensador.

El voltaje a través de la batería es simplemente\(V\). El voltaje a través del condensador es\(\frac{1}{C}q\). El voltaje a través de la resistencia es\(R\frac{dq}{dt}\). Finalmente, el voltaje a través del inductor es\(L\frac{d^2q}{dt^2}\). Por lo tanto, por la ley de tensión de Kirchoff, se deduce que

\[L \frac{d^{2} q}{d t^{2}}+R \frac{d q}{d t}+\frac{1}{C} q=V. \nonumber \]

Figura\(\PageIndex{1}\): Un circuito RLC en serie.

En la sección Resolver ecuaciones diferenciales de coeficientes constantes lineales se describirá en profundidad cómo se pueden obtener soluciones a ecuaciones diferenciales como las de los ejemplos.

Resumen de ecuaciones diferenciales ordinarias de coeficiente constante lineal

Las ecuaciones diferenciales son una herramienta matemática importante para modelar sistemas de tiempo continuo. Una subclase importante de estas es la clase de ecuaciones diferenciales ordinarias de coeficiente constante lineal. Las ecuaciones diferenciales ordinarias de coeficiente constante lineal son a menudo particularmente fáciles de resolver como se describirá en el módulo sobre soluciones a ecuaciones diferenciales ordinarias de coeficiente constante lineal y son útiles para describir una amplia gama de situaciones que surgen en ingeniería eléctrica y en otras campos.