3.8: Resolver ecuaciones diferenciales de coeficiente constante lineal

Introducción

El enfoque para resolver ecuaciones diferenciales ordinarias de coeficiente constante lineal es encontrar la forma general de todas las soluciones posibles a la ecuación y luego aplicar una serie de condiciones para encontrar la solución adecuada. Los dos tipos principales de problemas son los problemas de valor inicial, los cuales involucran restricciones en la solución y sus derivadas en un solo punto, y problemas de valor límite, que involucran restricciones en la solución o sus derivadas en varios puntos.

El número de condiciones iniciales necesarias para una ecuación diferencial de orden\(N\) th, que es el orden de la derivada de orden más alto, es\(N\), y siempre se garantiza una solución única si éstas se suministran. Los problemas de valor límite pueden ser un poco más complicados y no necesariamente tendrán una solución única o incluso una solución para un conjunto dado de condiciones. Así, este módulo se centrará exclusivamente en problemas de valor inicial.

Resolución de ecuaciones diferenciales ordinarias de coeficiente constante lineal

Considere alguna ecuación diferencial ordinaria de coeficiente constante lineal dada por\(Ax(t)=f(t)\), donde\(A\) es un operador diferencial de la forma

\[A=a_{n} \frac{d^{n}}{d t^{n}}+a_{n-1} \frac{d^{n-1}}{d t^{n-1}}+\ldots+a_{1} \frac{d}{d t}+a_{0} \nonumber \]

Dejar\(x_h(t)\) y\(x_p(t)\) ser dos funciones tal que\(Ax_h(t)=0\) y\(Ax_p(t)=f(t)\). Por la linealidad de\(A\), tenga en cuenta que\(A(x_h(t)+x_p(t))=0+f(t)=f(t)\). Así, la forma de la solución general\(x_g(t)\) a cualquier ecuación diferencial ordinaria de coeficiente constante lineal es la suma de una solución homogénea\(x_h(t)\) a la ecuación\(Ax=0\) y una solución particular\(x_p(t)\) que es específica de la función de forzamiento\(f(t)\).

Deseamos determinar las formas de las soluciones homogéneas y no homogéneas en toda generalidad para evitar restringir incorrectamente la forma de la solución antes de aplicar cualquier condición. De lo contrario, un conjunto válido de condiciones iniciales o de límite podría parecer que no tiene una trayectoria de solución correspondiente. La siguiente discusión muestra cómo lograr esto para ecuaciones diferenciales ordinarias de coeficiente constante lineal.

Encontrar la solución homogénea

Para encontrar la solución homogénea a\(Ax(t)=f(t)\), considere la ecuación diferencial\(Ax(t)=0\). Sabemos que las soluciones tienen la forma\(ce^{\lambda t}\) de algunas constantes complejas\(c\),\(\lambda\). Ya que\(Ace^{\lambda t} = 0\) para una solución, se deduce que

\[\left(a_{n} \frac{d^{n}}{d t^{n}}+a_{n-1} \frac{d^{n-1}}{d t^{n-1}}+\ldots+a_{1} \frac{d}{d t}+a_{0}\right) e^{\lambda t}=0, \nonumber \]

por lo que también se deduce que

\[a_{n} \lambda^{n}+a_{n-1} \lambda^{n-1} \ldots+a_{1} \lambda+a_{0}=0. \nonumber \]

Por lo tanto, los parámetros de los exponentes de solución son las raíces del polinomio anterior, denominado polinomio característico.

Para ecuaciones de orden dos o más, habrá varias raíces. Si todas las raíces son distintas, entonces la forma general de la solución homogénea es simplemente

\[x_{h}(t)=c_{1} e^{\lambda_{1} t}+\ldots+c_{n} e^{\lambda_{n} t}. \nonumber \]

Si una raíz tiene multiplicidad mayor que uno, las soluciones repetidas deben multiplicarse por cada potencias\(t\) de 0 a una menor que la multiplicidad raíz (para asegurar soluciones linealmente independientes). Por ejemplo, si\(\lambda_1\) tuviera multiplicidad 2 y\(\lambda_2\) tuviera multiplicidad 3, la solución homogénea sería

\[x_{h}(t)=c_{1} e^{\lambda_{1} t}+c_{2} t e^{\lambda_{1} t}+c_{3} e^{\lambda_{2} t}+c_{4} t e^{\lambda_{2} t}+c_{5} t^{2} e^{\lambda_{2} t} \nonumber \]

Ejemplo\(\PageIndex{1}\)

Considere el modelo de desintegración en el que una cantidad de un isótopo inestable disminuye a una velocidad proporcional a la cantidad de isótopo inestable restante. Así, la desintegración del isótopo es modelada por la ecuación diferencial de coeficiente constante lineal de primer orden

\[\frac{d x}{d t}+r x=0 \nonumber \]

donde\(r\) hay alguna tasa real. Esta ecuación diferencial podría resolverse fácilmente a través de una integración sencilla. Sin embargo, en su lugar se utilizarán los métodos descritos anteriormente. Tenga en cuenta que la función de forzamiento es cero, por lo que solo se necesita una solución homogénea. Es fácil ver que el polinomio característico es\(\lambda+r=0\), por lo que hay una raíz\(\lambda_1=r\). Así la solución es de la forma

\[x(t)=c_{1} e^{r t} \nonumber \]

Dada una tasa y una condición inicial, esto se puede aplicar a una situación específica. Por ejemplo, sabemos que el carbono-14 decae a una tasa de aproximadamente\(r=1.21\times 10^{−4}\) año\(^{−1}\), y si normalizamos la concentración natural de carbono-14 a\(x(0)=1\) la solución se vuelve\(x(t)=e^{−1.21\times 10^{−4}t}\). El conocimiento de esta curva sería útil para la datación basada en radioisótopos.

Encontrar la solución particular

Encontrar la solución particular es una tarea un poco más complicada que encontrar la solución homogénea. Un método formal, llamado variación de parámetros lo logra, y también hay varias heurísticas que pueden ser utilizadas. También se puede encontrar a través de la convolución de la entrada con la respuesta de impulso de la unidad, una vez que se conoce la respuesta de impulso de la unidad. Encontrar la solución particular a una ecuación diferencial se discute más adelante en el capítulo relativo a la transformación de Laplace, lo que simplifica enormemente el procedimiento para resolver ecuaciones diferenciales ordinarias de coeficiente constante lineal utilizando herramientas de dominio de frecuencia.

Ejemplo\(\PageIndex{2}\)

Considere el circuito RLC en serie que se muestra en la Figura\(\PageIndex{1}\). Este sistema se puede modelar usando ecuaciones diferenciales. Podemos usar las ecuaciones de voltaje para cada elemento del circuito y la ley de voltaje de Kirchoff para escribir una ecuación diferencial de coeficiente constante lineal de segundo orden que describa la carga en el condensador.

El voltaje a través de la batería es simplemente\(V\). El voltaje a través del condensador es\(\frac{1}{C}q\). El voltaje a través de la resistencia es\(R \frac{dq}{dt}\). Finalmente, el voltaje a través del inductor es\(L\frac{d^2q}{dt^2}\). Por lo tanto, por la ley de tensión de Kirchoff, se deduce que

\[L \frac{d^{2} q}{d t^{2}}+R \frac{d q}{d t}+\frac{1}{C} q=V \nonumber \]

Figura\(\PageIndex{1}\): Un circuito RLC en serie.

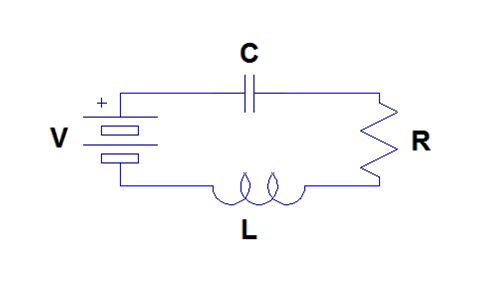
En primer lugar, se encuentra la solución homogénea. Es fácil ver que lo es el polinomio característico\(L \lambda^{2}+R \lambda+\frac{1}{C}=0\). Por lo tanto, las dos raíces son\(\lambda_{1}=\frac{-R-\sqrt{R^{2}-\frac{4 L}{C}}}{2 L}\) y\(\lambda_{2}=\frac{-R+\sqrt{R^{2}-\frac{4 L}{C}}}{2 L}\). A menudo, estos se establecen en términos del factor de atenuación\(\alpha=\frac{R}{2} \sqrt{\frac{C}{L}}\) y la frecuencia resonante\(\omega_{0}=\frac{1}{\sqrt{L C}}\). Así,\(\lambda_{1}=-\alpha-\sqrt{\alpha^{2}-\omega_{0}^{2}}\) y\(\lambda_{2}=-\alpha+\sqrt{\alpha^{2}-\omega_{0}^{2}}\).

Así, la ecuación homogénea es de la forma

\[ x_{h}(t)=c_{1} e^{-\alpha-\sqrt{\alpha^{2}-\omega_{0}^{2}}}+c_{2} e^{-\alpha+\sqrt{\alpha^{2}-\omega_{0}^{2}}}. \nonumber \]

Resulta que la respuesta a la función de forzamiento de fuente de voltaje constante es una constante, por lo que

\[x_{p}(t)=V C. \nonumber \]

Por lo tanto, la solución general es

\[x(t)=V C+c_{1} e^{-\alpha-\sqrt{\alpha^{2}-\omega_{0}^{2}} t}+c_{2} e^{-\alpha+\sqrt{\alpha^{2}-\omega_{0}^{2}} t} \nonumber \]

donde\(c_1\) y\(c_2\) dependen de las condiciones iniciales. El sistema demuestra una rica variedad de comportamientos basados en los valores relativos de\(\alpha\) y\(\omega_0\), que se anima al lector a explorar.

Resolver ecuaciones diferenciales

Las ecuaciones diferenciales ordinarias de coeficiente constante lineal son útiles para modelar una amplia variedad de sistemas de tiempo continuo. El enfoque para resolverlos es encontrar la forma general de todas las soluciones posibles a la ecuación y luego aplicar una serie de condiciones para encontrar la solución adecuada. Esto se hace encontrando la solución homogénea a la ecuación diferencial que no depende de la entrada de la función de forzamiento y una solución particular a la ecuación diferencial que sí depende de la entrada de la función de forzamiento.