1.3: Operaciones de señal
- Page ID
- 86592
Introducción
Este módulo analizará dos operaciones de señal que afectan el parámetro de tiempo de la señal, el cambio de tiempo y el escalado de tiempo. Estas operaciones son componentes muy comunes a los sistemas del mundo real y, como tales, deben entenderse a fondo a la hora de aprender sobre señales y sistemas.
Manipulación del parámetro de tiempo
Cambio de tiempo
El cambio de tiempo es, como su nombre indica, el desplazamiento de una señal en el tiempo. Esto se hace sumando o restando una cantidad del desplazamiento a la variable de tiempo en la función. Restar una cantidad positiva fija de la variable de tiempo desplazará la señal hacia la derecha (retardo) por la cantidad restada, mientras que sumar una cantidad positiva fija a la variable de tiempo desplazará la señal hacia la izquierda (avance) por la cantidad agregada.
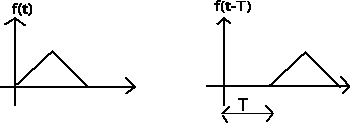
Escalado de tiempo
La escala de tiempo comprime o dilata una señal multiplicando la variable de tiempo por alguna cantidad. Si esa cantidad es mayor que uno, la señal se vuelve más estrecha y la operación se llama compresión, mientras que si la cantidad es menor a uno, la señal se hace más ancha y se llama dilatación.
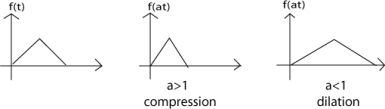
Ejemplo\(\PageIndex{1}\)
Dado\(f(t)\) nos gustaría trazar\(f(at−b)\).
Solución
La siguiente figura describe un método para lograrlo.
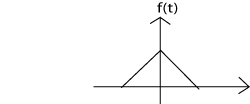 (a)
(a)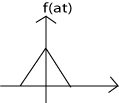 b)
b)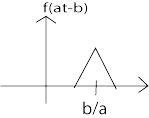 c)
c)
Figura\(\PageIndex{3}\): (a) Begin with \(f(t)\) (b) Then replace \(t\) with \(at\) to get \(f(at)\) (c) Finally, replace\(t\) con\(t−\frac{b}{a}\) para obtener\(f(a(t−\frac{b}{a}))=f(at−b)\)
Reversión de tiempo
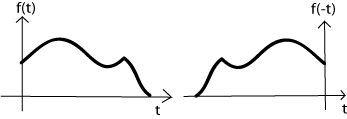
Una pregunta natural a considerar al aprender sobre el escalado de tiempo es: ¿Qué sucede cuando la variable de tiempo se multiplica por un número negativo? La respuesta a esto es la inversión del tiempo. Esta operación es la inversión del eje de tiempo, o voltear la señal sobre el eje y.
Demostración de Escalado y Cambio de Tiempo
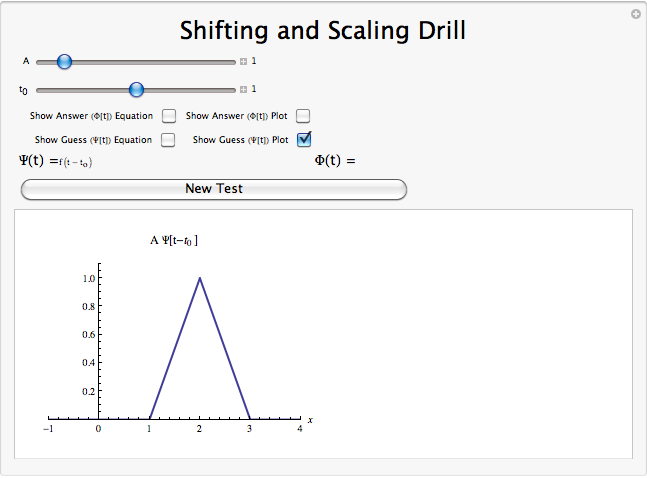
Resumen de Operaciones de Señal
Algunas operaciones comunes en las señales afectan el parámetro de tiempo de la señal. Uno de estos es el cambio de tiempo en el que se agrega una cantidad al parámetro de tiempo para avanzar o retrasar la señal. Otro es el escalado de tiempo en el que el parámetro de tiempo se multiplica por una cantidad para dilatar o comprimir la señal en el tiempo. En el caso de que la cantidad involucrada en esta última operación sea negativa, se produce la inversión de tiempo.


