1.6: Función de Impulso de Tiempo Continuo

Introducción

En ingeniería, a menudo nos ocupamos de la idea de que una acción ocurra en un momento determinado. Ya sea una fuerza en un punto en el espacio o alguna otra señal en un punto en el tiempo, vale la pena desarrollar alguna forma de definir cuantitativamente esto. Esto nos lleva a la idea de un impulso unitario, probablemente la segunda función más importante, junto a la compleja exponencial, en este curso de sistemas y señales.

Función Dirac Delta

La función delta Dirac, a menudo denominada impulso unitario o función delta, es la función que define la idea de un impulso unitario en tiempo continuo. Informalmente, esta función es aquella que es infinitesimalmente estrecha, infinitamente alta, pero se integra a una. Quizás la forma más sencilla de visualizar esto es como un pulso rectangular de\(a-\frac{\varepsilon}{2}\) a\(a+\frac{\varepsilon}{2}\) con una altura de\(\frac{1}{\varepsilon}\). A medida que tomamos el límite de esta configuración cuando\(\varepsilon\) se acerca a 0, vemos que el ancho tiende a cero y la altura tiende al infinito ya que el área total permanece constante en uno. La función de impulso a menudo se escribe como\(\delta(t)\).

\[\int_{-\infty}^{\infty} \delta(t) \mathrm{d} t=1 \nonumber \]

Figura\(\PageIndex{1}\): Esta es una forma de visualizar la función Delta de Dirac.

Figura\(\PageIndex{2}\): Como es bastante difícil dibujar algo que sea infinitamente alto, representamos al Dirac con una flecha centrada en el punto en que se aplica. Si queremos escalarlo, podemos escribir el valor por el que se escala junto al punto de la flecha. Se trata de un impulso unitario (sin escalado).

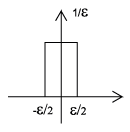
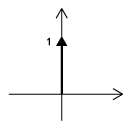
A continuación se muestra una breve lista de algunas propiedades importantes de la unidad impulsan sin entrar en detalle de sus pruebas.

Propiedades de Impulso de Unidad

• \(\delta(\alpha t)=\frac{1}{|\alpha|} \delta(t)\)
• \(\delta(t)=\delta(-t)\)
• \(\delta(t)=\frac{d}{dt} u(t)\), donde\(u(t)\) está el paso de la unidad.
• \(f(t) \delta(t)=f(0) \delta(t)\)

El último de estos es especialmente importante ya que da lugar a la propiedad de tamizado de la función dirac delta, que selecciona el valor de una función en un momento específico y es especialmente importante en el estudio de la relación de una operación llamada convolución con el análisis del dominio del tiempo lineal invariante sistemas. La propiedad de tamizado se muestra y se deriva a continuación.

\[\int_{-\infty}^{\infty} f(t) \delta(t) d t=\int_{-\infty}^{\infty} f(0) \delta(t) d t=f(0) \int_{-\infty}^{\infty} \delta(t) d t=f(0) \nonumber \]

Demostración de limitación de impulso unitario

Figura\(\PageIndex{3}\): Haga clic en la imagen en miniatura de arriba (cuando esté en línea) para descargar un reproductor de Mathematica interactivo que demuestre la función de impulso de tiempo continuo.

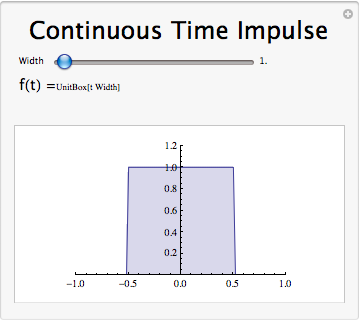
Resumen de impulso de unidad de tiempo continuo

La función de impulso continuo de la unidad de tiempo, también conocida como la función delta de Dirac, es de gran importancia para el estudio de señales y sistemas. Informalmente, es una función con altura infinita y ancho infinitesimal que se integra a uno, lo que puede verse como el comportamiento limitante de un rectángulo de área unitaria a medida que se estrecha mientras conserva el área. Tiene varias propiedades importantes que volverán a aparecer al estudiar sistemas.