6.4: Propiedades del CTFS
- Page ID
- 86533
Introducción
En este módulo discutiremos las propiedades básicas de la Serie de Fourier de Tiempo Continuo. Comenzaremos refrescando su memoria de nuestras ecuaciones básicas de la serie de Fourier:
\[f(t)=\sum_{n=-\infty}^{\infty} c_{n} e^{j \omega_{0} n t} \nonumber \]
\[c_{n}=\frac{1}{T} \int_{0}^{T} f(t) e^{-\left(j \omega_{0} n t\right)} \mathrm{d} t \nonumber \]
Dejar\(\mathscr{F}(\cdot)\) denotar la transformación de\(f(t)\) a los coeficientes de Fourier
\[\mathscr{F}(f(t))=\forall n, n \in \mathbb{Z}:\left(c_{n}\right) \nonumber \]
\(\mathscr{F}(\cdot)\)mapea funciones complejas valoradas a secuencias de números complejos.
Linealidad
\(\mathscr{F}(\cdot)\)es una transformación lineal.
Teorema\(\PageIndex{1}\)
Si\(\mathscr{F}(f(t))=c_{n}\) y\(\mathscr{F}(g(t))=d_{n}\). Entonces
\[\forall \alpha, \alpha \in \mathbb{C}:\left(\mathscr{F}(\alpha f(t))=\alpha c_{n}\right) \nonumber \]
y
\[\mathscr{F}(f(t)+g(t))=c_{n}+d_{n} \nonumber \]
Prueba
Fácil. Justa linealidad de integral.
\ [\ begin {align}
\ mathscr {F} (f (t) +g (t)) &=\ forall n, n\ in\ mathbb {Z}:\ left (\ int_ {0} ^ {T} (f (t) +g (t)) e^ {-\ left (j\ omega_ {0} n t\ derecha)}\ mathrm {d} t\ derecha)\ nonumber\\
&=\ forall n, n\ in\ mathbb {Z}:\ izquierda (\ frac {1} {T}\ int_ {0} ^ {T} f (t) e^ {-\ izquierda (j\ omega_ {0} n t\ derecha)}\ mathrm { d} t+\ frac {1} {T}\ int_ {0} ^ {T} g (t) e^ {-\ izquierda (j\ omega_ {0} n t\ derecha)}\ mathrm {d} t\ derecha)\ nonumber\\
&=\ forall n, n\ in\ mathbb {Z}:\ izquierda (c_ {n} +d_ {}\ derecha)\ nonumber\\
&=c_ {n} +d_ {n}
\ end {align}\ nonumber\]
Desviación
El desplazamiento en el tiempo equivale a un desplazamiento de fase de los coeficientes de Fourier.
Teorema\(\PageIndex{2}\)
\(\mathcal{F}\left(f\left(t-t_{0}\right)\right)=e^{-\left(j \omega_{0} n t_{0}\right)} c_{n}\)si\(c_{n}=\left|c_{n}\right| e^{j \angle\left(c_{n}\right)}\), entonces
\[\left|e^{-\left(j \omega_{0} n t_{0}\right)} c_{n}\right|=\left|e^{-\left(j \omega_{0} n t_{0}\right)}\right|\left|c_{n}\right|=\left|c_{n}\right| \nonumber \]
\[\angle\left(e^{-\left(i \omega_{0} t_{0} n\right)}\right)=\angle\left(c_{n}\right)-\omega_{0} t_{0} n \nonumber \]
Prueba
\ [\ begin {align}
\ mathscr {F}\ left (f\ left (t-t_ {0}\ right)\ right) &=\ forall n, n\ in\ mathbb {Z}:\ left (\ frac {1} {T}\ int_ {0} ^ {T} f\ left (t-t_ {0}\ right) e^ {-\ left (j\ omega_ {0} n t\ derecha)}\ mathrm {d} t\ derecha)\ nonumber\\
&=\ forall n, n\ in\ mathbb {Z}:\ left (\ frac {1} {T}\ int_ {-t_ {0}} ^ { t-t_ {0}} f\ izquierda (t-t_ {0}\ derecha) e^ {-\ izquierda (j\ omega_ {0} n\ izquierda (t-t_ {0}\ derecha)\ derecha)} e^ {-\ izquierda (j\ omega_ {0} n t_ {0}\ derecha)}\ mathrm {d} t\ derecha)\ nonumber\\
=\ forall n, n\ in\ mathbb {Z}:\ izquierda (\ frac {1} {T}\ int_ {-t_ {0}} ^ {t-t_ {0}} f (\ tilde {t}) e^ {-\ izquierda (j\ omega_ {0} n\ tilde {t}\ derecha)} e^ {-\ izquierda (j \ omega_ {0} n t_ {0}\ derecha)}\ mathrm {d} t\ derecha)\ nonumber\\
&=\ forall n, n\ in\ mathbb {Z}:\ izquierda (e^ {-\ izquierda (j\ omega_ {0} n\ tilde {t}\ derecha)} c_ {n}\ derecha)
\ end {nonalign}\ umber\]
Relación de Parseval
\[\int_{0}^{T}(|f(t)|)^{2} \mathrm{d} t=T \sum_{n=-\infty}^{\infty}\left(\left|c_{n}\right|\right)^{2} \nonumber \]
La relación de Parseval nos dice que la energía de una señal es igual a la energía de su transformada de Fourier.
Nota
Parseval nos dice que la serie de Fourier se mapea\(L^2([0,T])\) a\(l^2(\mathbb{Z})\).
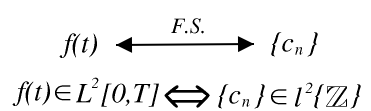
Figura\(\PageIndex{1}\)
Ejercicio\(\PageIndex{1}\)
\(f(t)\)Para tener “energía finita”, ¿cómo\(c_n\) hacen los\(n \rightarrow \infty\)?
- Contestar
-
\(\left(\left|c_{n}\right|\right)^{2}<\infty\)para\(f(t)\) tener energía finita.
Ejercicio\(\PageIndex{2}\)
Si\(\forall n,|n|>0:\left(c_{n}=\frac{1}{n}\right)\), ¿es\(f \in L^{2}([0, T])\)?
- Contestar
-
Sí, porque\(\left(\left|c_{n}\right|\right)^{2}=\frac{1}{n}\), que es sumable.
Ejercicio\(\PageIndex{3}\)
Ahora bien,\(\forall n,|n|>0:\left(c_{n}=\frac{1}{\sqrt{n}}\right)\) ¿si es\(f \in L^{2}([0, T])\)?
- Contestar
-
No, porque\(\left(\left|c_{n}\right|\right)^{2}=\frac{1}{n}\), que no es sumable.
La tasa de decaimiento de la serie de Fourier determina si\(f(t)\) tiene energía finita.
Demostración del teorema de los análisis

Propiedades de simetría
Regla\(\PageIndex{1}\): Even Signals
Señales pares
\ (\ begin {array} {l}
f (t) =f (-t)\\
\ izquierda\ |c_ {n}\ derecha\ |=\ izquierda\ |c_ {-n}\ derecha\ |
\ fin {array}\)
Prueba
\ (\ begin {array} {l}
c_ {n} =\ frac {1} {T}\ int_ {0} ^ {T} f (t)\ exp\ left (-j\ omega_ {0} n t\ derecha) d t\
=\ frac {1} {T}\ int_ {0} ^ {\ frac {T} {2}} f (t)\ exp\ izquierda (-j\ omega_ {0} n t\ derecha) d t+\ frac {1} {T}\ int_ {\ frac {T} {2}} ^ {T} f (t)\ exp\ izquierda (-j\ omega_ {0} n t\ derecha) d t\\
=\ frac { 1} {T}\ int_ {0} ^ {\ frac {T} {2}} f (-t)\ exp\ izquierda (-j\ omega_ {0} n t\ derecha) d t+\ frac {1} {T}\ int_ {\ frac {T} {2}} ^ {T} f (-t)\ exp\ izquierda (-j\ omega_ {0} n t\ derecha) d t\\
=\ frac {1} {T}\ int_ {0} ^ {T} f (t)\ izquierda [\ exp\ izquierda (j\ omega_ {0} n t\ derecha) d t+\ exp\ izquierda (-j\ omega_ {0} n t\ derecha)\ derecha] d t\\
=\ frac {1} {T}\ int_ {0} ^ {T} f (t) 2\ cos\ izquierda (\ omega_ {0} n t\ derecha) d t
\ end {array}\)
Regla\(\PageIndex{2}\): Odd Signals
Señales impares
\ (\ begin {array} {l}
f (t) =-f (-t)\\
c_ {n} =c_ {-n} ^ {*}
\ end {array}\)
Prueba
\ (\ begin {array} {l}
c_ {n} =\ frac {1} {T}\ int_ {0} ^ {T} f (t)\ exp\ left (-j\ omega_ {0} n t\ derecha) d t\
=\ frac {1} {T}\ int_ {0} ^ {\ frac {\ pi} {2}} (f)\ exp\ izquierda (-j\ omega_ {0} n t\ derecha) d t+\ frac {1} {T}\ int_ {\ frac {T} {2}} ^ {T} f (t)\ exp\ izquierda (-j\ omega_ {0} n t\ derecha) d t\\
=\ frac {1} {T}\ int_ {0} ^ {\ frac {T} {2}} f (t)\ exp\ izquierda (-j\ omega_ {0} n t\ derecha) d t-\ frac {1} {T}\ int_ {\ frac {T} {2}} ^ {T} f (-t)\ exp\ izquierda (j\ omega_ {0} n t\ derecha) d t\\
=-\ frac {1} {T}\ int_ {0} ^ {T} f (t)\ izquierda [\ exp\ izquierda (j\ omega_ {0} n t\ derecha) d t-\ exp\ izquierda (-j\ omega_ {0} n t\ derecha)\ derecha] d t\\
=-\ frac {1} {T}\ int_ {0} ^ {T} f (t) 2 j\ sin\ izquierda (\ omega_ {0} n t\ derecha) d t
\ end {array}\)
Regla\(\PageIndex{3}\): Real Signals
Señales Reales
\ (\ begin {array} {l}
f (t) =f^ {*} (t)\\
c_ {n} =c_ {-n} ^ {*}
\ end {array}\)
Prueba
\ (\ begin {array} {l}
c_ {n} =\ frac {1} {T}\ int_ {0} ^ {T} f (t)\ exp\ left (-j\ omega_ {0} n t\ derecha) d t\
=\ frac {1} {T}\ int_ {0} ^ {\ frac {T} {2}} f (t)\ exp\ izquierda (-j\ omega_ {0} n t\ derecha) d t+\ frac {1} {T}\ int_ {\ frac {T} {2}} ^ {T} f (t)\ exp\ izquierda (-j\ omega_ {0} n t\ derecha) d t\\
=\ frac { 1} {T}\ int_ {0} ^ {\ frac {T} {2}} f (-t)\ exp\ izquierda (-j\ omega_ {0} n t\ derecha) d t+\ frac {1} {T}\ int_ {\ frac {T} {2}} ^ {T} f (-t)\ exp\ izquierda (-j\ omega_ {0} n t\ derecha) d t\\
=\ frac {1} {T}\ int_ {0} ^ {T} f (t)\ izquierda [\ exp\ izquierda (j\ omega_ {0} n t\ derecha) d t+\ exp\ izquierda (-j\ omega_ {0} n t\ derecha)\ derecha] d t\\
=\ frac {1} {T}\ int_ {0} ^ {T} f (t) 2\ cos\ izquierda (\ omega_ {0} n t\ derecha) d t
\ end {array}\)
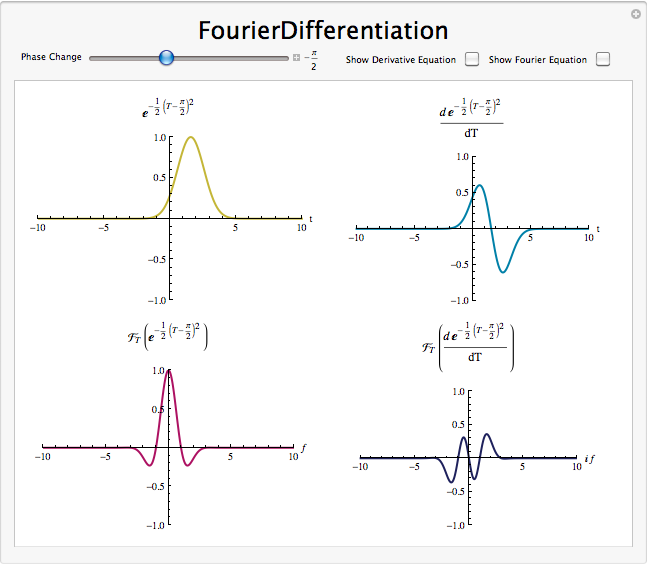
Diferenciación en el Dominio de Fourier
\[\left(\mathcal{F}(f(t))=c_{n}\right) \Rightarrow\left(\mathcal{F}\left(\frac{d f(t)}{d t}\right)=j n \omega_{0} c_{n}\right) \nonumber \]
Desde
\[f(t)=\sum_{n=-\infty}^{\infty} c_{n} e^{j \omega_{0} n t} \nonumber \]
entonces
\ [\ begin {align}
\ frac {d} {dt} f (t) &=\ suma_ {n=-\ infty} ^ {\ infty} c_ {n}\ frac {d e^ {j\ omega_0 n t}} {d t}\ nonumber\\
&=\ suma_ {n=-\ infty} ^ {\ infty} c_ {} j\ omega_ {0} n e^ {i\ omega_ {0} n t}
\ end {align}\ nonumber\]
Un diferenciador atenúa las frecuencias bajas\(f(t)\) y acentúa las frecuencias altas. Elimina tendencias generales y acentúa áreas de fuerte variación.
Nota
Una forma común de medir matemáticamente la suavidad de una función\(f(t)\) es ver cuántas derivadas son energía finita.
Esto se hace observando los coeficientes de Fourier de la señal, específicamente qué tan rápido decaen como\(n \rightarrow \infty\). Si\(\mathscr{F}(f(t))=c_{n}\) y\(|c_n|\) tiene la forma\(\frac{1}{n^k}\), entonces\(\mathscr{F}\left(\frac{\mathrm{d}^{m} f(t)}{\mathrm{d} t^{m}}\right)=\left(j n \omega_{0}\right)^{m} c_{n}\) y tiene la forma\(\frac{n^m}{n^k}\). Entonces, para que el derivado\(m\) th tenga energía finita, necesitamos
\[\sum_{n}\left(\left|\frac{n^{m}}{n^{k}}\right|\right)^{2}<\infty \nonumber \]
\(\frac{n^m}{n^k}\)decae más rápido de\(\frac{1}{n}\) lo que implica que
\[2k−2m>1 \nonumber \]
o
\[k>\frac{2m+1}{2} \nonumber \]
Así, la tasa de decaimiento de la serie de Fourier dicta la suavidad.
Demostración de diferenciación de Fourier
Integración en el dominio de Fourier
Si
\[\mathscr{F}(f(t))=c_{n} \nonumber \]
entonces
\[\mathscr{F}\left(\int_{-\infty}^{t} f(\tau) \mathrm{d} \tau\right)=\frac{1}{j \omega_{0} n} c_{n} \nonumber \]
Nota
Si\(c_{0} \neq 0\), esta expresión no tiene sentido.
La integración acentúa las bajas frecuencias y atenúa las frecuencias altas. Los integradores sacan a relucir las tendencias generales en las señales y suprimen la variación a corto plazo (que en muchos casos es ruido). Los integradores son mucho más agradables que los diferenciadores.
Demostración de integración de Fourier

Multiplicación y convolución de señales
Dada una señal\(f(t)\) con coeficientes de Fourier\(c_n\) y una señal\(g(t)\) con coeficientes de Fourier\(d_n\), podemos definir una nueva señal,\(y(t)\), donde\(y(t)=f(t)g(t)\). Encontramos que la representación de la Serie de Fourier de\(y(t)\)\(e_n\),, es tal que\(e_{n}=\sum_{i=-\infty}^{\infty} c_{k} d_{n-k}\). Esto quiere decir que la multiplicación de señal en el dominio del tiempo es equivalente a la convolución de señal en el dominio de frecuencia, y viceversa: la multiplicación de señal en el dominio de frecuencia es equivalente a la convolución de señal en el dominio del tiempo. La prueba de ello es la siguiente
\ [\ begin {align}
e_ {n} &=\ frac {1} {T}\ int_ {0} ^ {T} f (t) g (t) e^ {-\ izquierda (j\ omega_ {0} n t\ derecha)}\ mathrm {d} t\ nonumber\\
&=\ frac {1} {T}\ int_ {0} ^ {^ T}\ sum_ {k=-\ infty} ^ {\ infty} c_ {k} e^ {j\ omega_ {0} k t} g (t) e^ {-\ izquierda (j\ omega_ {0} n t\ derecha)}\ mathrm {d} t\ nonumber\\
&=\ sum_ {k=-\ infty} ^ {\ infty} c_ {k}\ izquierda (\ frac {1} {T}\ int_ {0} ^ {T} g (t) e^ {-\ izquierda (j\ omega_ {0} (n-k) t\ derecha)}\ mathrm {d} t\ derecha)\ nonumber\\
&= _ {k=-\ infty} ^ {\ infty} c_ {k} d_ {n-k}
\ end {align}\ nonumber\]
para más detalles, consulte la sección sobre Convolución de la señal y el CTFS (Sección 4.3).
Conclusión
Al igual que otras transformadas de Fourier, el CTFS tiene muchas propiedades útiles, incluyendo linealidad, igual energía en los dominios de tiempo y frecuencia, y análogos para desplazamiento, diferenciación e integración.
| Propiedad | Señal | CTFS |
| Linealidad | \(a x(t)+b y(t)\) | \(a X(f)+b Y(f)\) |
| Cambio de tiempo | \(x(t-\tau)\) | \(X(f) e^{-j 2 \pi f \tau / T}\) |
| Modulación de tiempo | \(x(t) e^{j 2 \pi f \tau / T}\) | \(X(f-k)\) |
| Multiplicación | \(x(t)y(t)\) | \(X(f)*Y(f)\) |
| Convolución Continua | \(x(t)*y(t)\) | \(X(f)Y(f)\) |


