6.6: Convergencia de la Serie de Fourier
- Page ID
- 86543
Introducción
Antes de mirar este módulo, ojalá te hayas convencido plenamente del hecho de que cualquier función periódica,\(f(t)\), puede representarse como una suma de sinusoides complejos (Sección 1.4). Si no lo es, intente mirar hacia atrás en las cosas propias en pocas palabras (Sección 14.4) o las funciones propias de los sistemas LTI (Sección 14.5). Hemos demostrado que podemos representar una señal como la suma de exponenciales a través de las ecuaciones de la Serie de Fourier a continuación:
\[f(t)=\sum_{n} c_{n} e^{j \omega_{0} n t} \label{6.35} \]
\[c_{n}=\frac{1}{T} \int_{0}^{T} f(t) e^{-\left(j \omega_{0} n t\right)} d t \label{6.36} \]
Joseph Fourier insistió en que estas ecuaciones eran ciertas, pero no pudo probarlo. Lagrange ridiculizó públicamente a Fourier, y dijo que solo las funciones continuas pueden ser representadas por la Ecuación\ ref {6.35} (de hecho demostró que la Ecuación\ ref {6.35} se mantiene para funciones de tiempo continuo). Sin embargo, ahora sabemos que la verdad real se encuentra entre las posiciones de Fourier y Lagrange.
Entendiendo la Verdad
Formulando nuestra pregunta matemáticamente, vamos
\[f_{N}^{\prime}(t)=\sum_{n=-N}^{N} c_{n} e^{j \omega_{0} n t} \nonumber \]
donde\(c_n\) es igual a los coeficientes de Fourier de\(f(t)\) (ver Ecuación\ ref {6.36}).
\(f_{N}^{\prime}(t)\)es una “reconstrucción parcial” del\(f(t)\) uso de los primeros coeficientes de\(2N+1\) Fourier. \(f_{N}^{\prime}\)se aproxima\(f(t)\), con la aproximación cada vez mejor a medida que\(N\) se hace grande. Por lo tanto, podemos pensar en el conjunto\(\left\{\forall N, N=\{0,1, \ldots\}:\left(\frac{\mathrm{d} f_{N}(t)}{\mathrm{d}}\right)\right\}\) como una secuencia de funciones, cada una aproximándose\(f(t)\) mejor que la anterior.
La pregunta es, ¿converge a esta secuencia\(f(t)\)? ¿Hace\( f_{N}^{\prime}(t) \rightarrow f(t)\) como\(N \rightarrow \infty\)? Intentaremos responder a esta pregunta pensando en la convergencia de dos maneras diferentes:
- Mirando la energía de la señal de error:
\[e_{N}(t)=f(t)-f_{N}^{\prime}(t) \nonumber \]
- \(\displaystyle{\lim_{N \to \infty}} \frac{d f_{N}(t)}{d}\)Mirando a cada punto y comparando con\(f(t)\).
Enfoque #1
\(e_N(t)\)Sea la diferencia (es decir, error) entre la señal\(f(t)\) y su reconstrucción parcial\(f_N^{\prime}\)
\[e_{N}(t)=f(t)-f_{N}^{\prime}(t) \nonumber \]
Si\(f(t) \in L^{2}([0, T])\) (energía finita), entonces la energía de\(e_{N}(t) \rightarrow 0\) como\(N \rightarrow \infty\) es
\[\int_{0}^{T}\left(\left|e_{N}(t)\right|\right)^{2} \mathrm{d} t=\int_{0}^{T}\left(f(t)-f_{N}^{\prime}(t)\right)^{2} \mathrm{d} t \rightarrow 0 \nonumber \]
Podemos probar esta ecuación usando la relación de Parseval:
\[\lim_{N \rightarrow \infty} \int_{0}^{T}\left(\left|f(t)-f_{N}^{\prime}(t)\right|\right)^{2} \mathrm{d} t=\lim_{N \rightarrow \infty} \sum_{N=-\infty}^{\infty}\left(\left|\mathscr{F}_{n}(f(t))-\mathscr{F}_{n}\left(\frac{\mathrm{d} f_{N}(t)}{\mathrm{d}}\right)\right|\right)^{2}=\lim_{N \rightarrow \infty} \sum_{|n|>N}\left(\left|c_{n}\right|\right)^{2}=0 \nonumber \]
donde la última ecuación antes de cero es la suma de cola de la Serie de Fourier, que se acerca a cero porque\(f(t) \in L^{2}([0, T])\). Dado que los sistemas físicos responden a la energía, la Serie de Fourier proporciona una representación adecuada para toda la energía\(f(t) \in L^{2}([0, T])\) finita equivalente a lo largo de un período.
Enfoque #2
El hecho de que no\(e_{N} \rightarrow 0\) dice nada sobre\(f(t)\) y\(\displaystyle{\lim_{N \rightarrow \infty}} \frac{\mathrm{d} f_{N}(t)}{\mathrm{d}}\) ser igual en un momento dado. Tome las dos funciones que se muestran a continuación, por ejemplo:
 (a)
(a)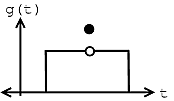 b)
b)
Figura\(\PageIndex{1}\)
Dadas estas dos funciones\(g(t)\),\(f(t)\) y, entonces podemos ver eso para todos\(t\)\(f(t) \neq g(t)\), pero
\[\int_{0}^{T}(|f(t)-g(t)|)^{2} \mathrm{d} t=0 \nonumber \]
De esto podemos ver las siguientes relaciones:
convergencia de energía convergencia\(\neq\) puntual
convergencia puntual\(\Rightarrow\) convergencia en\(L^2([0,T])\)
No obstante, no es cierto lo contrario de la afirmación anterior.
Resulta que si\(f(t)\) tiene una discontinuidad (como se puede ver en la figura de\(g(t)\) arriba) en\(t_0\), entonces
\[f\left(t_{0}\right) \neq \lim_{N \rightarrow \infty} \frac{\mathrm{d} f_{N}\left(t_{0}\right)}{\mathrm{d}} \nonumber \]
Pero siempre y cuando\(f(t)\) cumpla con algunas otras condiciones bastante suaves, entonces
\[f\left(t^{\prime}\right)=\lim_{N \rightarrow \infty} \frac{\left.\mathrm{d} f_{N}\left(t^{\prime}\right)\right)}{\mathrm{d}} \nonumber \]
si\(f(t)\) es continuo en\(t=t^{\prime}\).
Estas condiciones se conocen como las Condiciones de Dirichlet.
Condiciones de Dirichlet
El nombre del matemático alemán Peter Dirichlet, las condiciones de Dirichlet son las condiciones suficientes para garantizar la existencia y convergencia energética de la Serie de Fourier.
La condición débil de Dirichlet para la serie de Fourier
Para que exista la Serie de Fourier, los coeficientes de Fourier deben ser finitos. La Condición Débil Dirichlet lo garantiza. En esencia dice que la integral del valor absoluto de la señal debe ser finita.
Teorema\(\PageIndex{1}\): Weak Dirichlet Condition for the Fourier Series
Los coeficientes de la Serie de Fourier son finitos si
\[\int_{0}^{T}|f(t)| d t<\infty \nonumber \]
Prueba
Esto se puede mostrar a partir de la magnitud de los coeficientes de la Serie de Fourier:
\[\left|c_{n}\right|=\left|\frac{1}{T} \int_{0}^{T} f(t) e^{-\left(j \omega_{0} n t\right)} d t\right| \leq \frac{1}{T} \int_{0}^{T}\left|f(t) \| e^{-\left(j \omega_{0} n t\right)}\right| d t \nonumber \]
Recordando nuestros exponenciales complejos (Sección 1.8), sabemos que en la ecuación anterior\(\left|e^{-\left(j \omega_{0} n t\right)}\right|=1\), que nos da:
\ [\ begin {align}
\ izquierda|c_ {n}\ derecha|\ leq &\ frac {1} {T}\ int_ {0} ^ {T} |f (t) | d t<\ infty\\
&\ Rightarrow\ izquierda (\ izquierda|c_ {n}\ derecha|<\ infty\ derecha)
\ end align {}\ nonumber\]
Nota
Si tenemos la función:
\[\forall t, 0<t \leq T:\left(f(t)=\frac{1}{t}\right) \nonumber \]
entonces debes tener en cuenta que esta función falla en la condición anterior porque:
\[\int_{0}^{T}\left|\frac{1}{t}\right| \mathrm{d} t=\infty \nonumber \]
Las fuertes condiciones de Dirichlet para la serie de Fourier
Para que exista la Serie de Fourier, se deben cumplir las dos condiciones siguientes (junto con la Condición de Dirichlet Débil):
- En un periodo, sólo\(f(t)\) tiene un número finito de mínimos y máximos.
- En un periodo,\(f(t)\) tiene sólo un número finito de discontinuidades y cada una es finita.
Estas son las que nos referimos como las Condiciones Fuertes de Dirichlet. En teoría podemos pensar en señales que violen estas condiciones,\(\sin(\log t)\) por ejemplo. Sin embargo, no es posible crear una señal que viole estas condiciones en un laboratorio. Por lo tanto, cualquier señal del mundo real tendrá una representación de Fourier.
Ejemplo\(\PageIndex{1}\)
Supongamos que tenemos la siguiente función e igualdad:
\[f^{\prime}(t)=\lim_{N \rightarrow \infty} \frac{\mathrm{d} f_{N}(t)}{\mathrm{d}} \nonumber \]
Si\(f(t)\) cumple con las tres condiciones de las Condiciones de Dirichlet Fuerte, entonces
\[f(\tau)=f^{\prime}(\tau) \nonumber \]
en cada\(\tau\) una de las cuales\(f(t)\) es continua. Y donde\(f(t)\) es discontinuo,\(f^{\prime}(t)\) está el promedio de los valores a la derecha y a la izquierda.
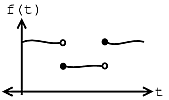 (a)
(a)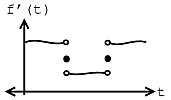 b)
b)Nota
Las funciones que fallan las fuertes condiciones de Dirchlet son bastante patológicas -como ingenieros, no estamos muy interesados en ellas.


