9.5: Convolución de Tiempo Discreta y DTFT

Última actualización
Guardar como PDF

Page ID: 86465

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Introducción

Este módulo analiza la convolución de señales discretas en los dominios de tiempo y frecuencia.

La convolución de tiempo discreto

Transformada de Fourier Tiempo Discreto

El DTFT transforma una señal discreta de longitud infinita en el dominio del tiempo en una señal continua de longitud finita (o\(2 \pi\) -periódica) en el dominio de la frecuencia.

DTFT

\[X(\omega)=\sum_{n=-\infty}^{\infty} x(n) e^{-(j \omega n)} \nonumber \]

Inverso DTFT

\[x(n)=\frac{1}{2 \pi} \int_{0}^{2 \pi} X(\omega) e^{j \omega n} d \omega \nonumber \]

Demostración

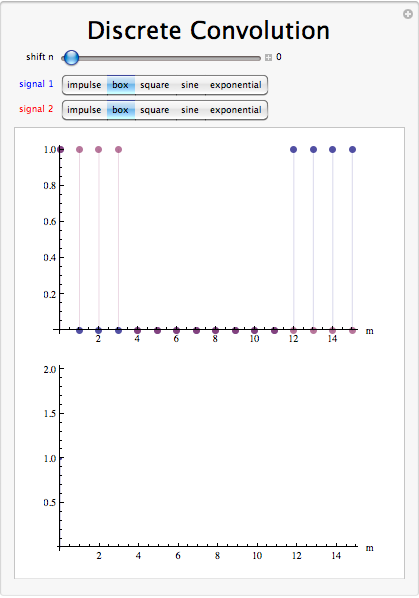
DiscreteConvolutionDemo — Figura\(\PageIndex{1}\): Interactuar (cuando esté en línea) con un CDF de Mathematica demostrando la Convolución Discreta. Para Descargar, haga clic derecho y guárdalo como .cdf.

Suma de convolución

Como se mencionó anteriormente, la suma de convolución proporciona una forma concisa y matemática de expresar la salida de un sistema LTI basado en una señal de entrada arbitraria de tiempo discreto y la respuesta de impulso del sistema. La suma de convolución se expresa como

\[y[n]=\sum_{k=-\infty}^{\infty} x[k] h[n-k] \nonumber \]

Al igual que con el tiempo continuo, la convolución está representada por el símbolo\(*\), y puede escribirse como

\[y[n]=x[n] * h[n] \nonumber \]

La convolución es conmutativa. Para mayor información sobre las características de la convolución, lea sobre las Propiedades de Convolución (Sección 3.4).

Teorema de convolución

Dejar\(f\) y\(g\) ser dos funciones con convolución\(f*g\). Dejar\(F\) ser el operador de transformada de Fourier. Entonces

\[F(f * g)=F(f) \cdot F(g) \nonumber \]

\[F(f \cdot g)=F(f) * F(g) \nonumber \]

Al aplicar la transformada inversa de Fourier\(F^{−1}\), podemos escribir:

\[f * g=F^{-1}(F(f) \cdot F(g)) \nonumber \]

Conclusión

La transformada de Fourier de una convolución es el producto puntual de las transformadas de Fourier. En otras palabras, la convolución en un dominio (por ejemplo, el dominio del tiempo) corresponde a la multiplicación por puntos en el otro dominio (por ejemplo, el dominio de la frecuencia).