10.2: Teorema de Muestreo

Introducción

Con la introducción del concepto de muestreo de señal, que produce una señal de tiempo discreta al seleccionar los valores de la señal de tiempo continua en puntos espaciados uniformemente en el tiempo, ahora es posible discutir uno de los resultados más importantes en el procesamiento de la señal, el teorema de muestreo de Nyquist-Shannon. A menudo llamado simplemente teorema de muestreo, este teorema se refiere a señales, conocidas como señales de banda limitada, con espectros que son cero para todas las frecuencias con valor absoluto mayor o igual a un cierto nivel. El teorema implica que existe una frecuencia de muestreo suficientemente alta a la que una señal de banda limitada se puede recuperar exactamente de sus muestras, lo que es un paso importante en el procesamiento de señales de tiempo continuas utilizando las herramientas de procesamiento de señal de tiempo discreto.

Teorema de muestreo de Nyquist-Shannon

Declaración del Teorema de Muestreo

El teorema de muestreo de Nyquist-Shannon se refiere a señales con transformaciones de Fourier de tiempo continuas que son solo distintas de cero en el intervalo\((−B,B)\) para alguna constante\(B\). Se dice que tal función está limitada en banda a\((−B,B)\). Esencialmente, el teorema del muestreo ya se ha introducido implícitamente en el módulo anterior relativo al muestreo. Dada una señal de tiempo continua\(x\) con transformada de Fourier de tiempo continuo\(X\), recuerde que el espectro\(X_s\) de señal muestreada\(x_s\) con periodo de muestreo\(T_s\) viene dado por

\[X_{s}(\omega)=\frac{1}{T_{s}} \sum_{k=-\infty}^{\infty} X\left(\frac{\omega-2 \pi k}{T_{s}}\right). \nonumber \]

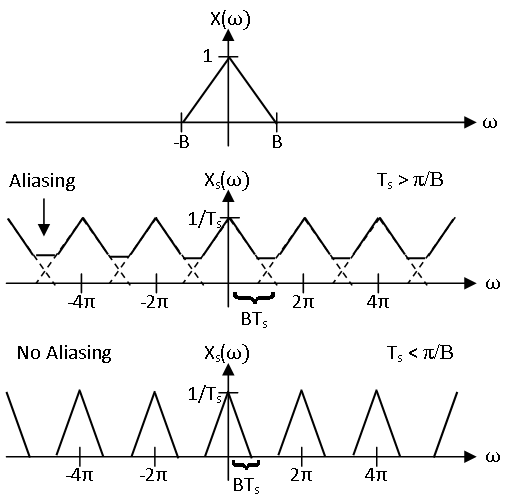
Anteriormente se había señalado que si\(x\) se limita a banda\((−\pi/T_s,\pi/T_s)\), el periodo de\(X_s\) centrado alrededor del origen tiene la misma forma que\(X\) escalado en frecuencia ya que no se produce aliasing. Esto se ilustra en la Figura\(\PageIndex{1}\). Por lo tanto, si dos señales de tiempo continuas\((−\pi/T_s,\pi/T_s)\) limitadas en banda cualesquiera muestreadas a la misma señal, tendrían la misma transformada de Fourier de tiempo continuo y, por lo tanto, serían idénticas. Por lo tanto, para cada señal de tiempo discreta hay una señal de tiempo continua\((−\pi/T_s,\pi/T_s)\) limitada en banda única que muestrea la señal de tiempo discreta con periodo de muestreo\(T_s\). Por lo tanto, esta señal de\((−\pi/T_s,\pi/T_s)\) banda limitada se puede encontrar a partir de las muestras invirtiendo esta bijección.

Esta es la esencia del teorema del muestreo. De manera más formal, el teorema de muestreo establece lo siguiente. Si una señal\(x\) está limitada en banda a\((−B,B)\), está completamente determinada por sus muestras con frecuencia de muestreo\(\omega_s=2B\). Es decir,\(x\) puede reconstruirse exactamente a partir de sus muestras\(x_s\) con frecuencia de muestreo\(\omega_s=2B\). La frecuencia angular a menudo\(2B\) se llama la velocidad angular Nyquist. Equivalentemente, esto se puede afirmar en términos del periodo de muestreo\(T_s=2 \pi / \omega_s\). Si una señal\(x\) es de banda limitada a\((−B,B)\), está completamente determinada por sus muestras con periodo de muestreo\(T_s=\pi/B\). Es decir,\(x\) puede reconstruirse exactamente a partir de sus muestras\(x_s\) con periodo de muestreo\(T_s\).

Figura\(\PageIndex{1}\): Se muestra el espectro de señales de banda limitada así como los espectros de sus muestras a velocidades por encima y por debajo de la frecuencia de Nyquist. Como se muestra, no se produce ningún aliasing por encima de la frecuencia Nyquist, y el periodo del espectro de muestras centrado alrededor del origen tiene la misma forma que el espectro de la señal original escalado en frecuencia. Por debajo de la frecuencia Nyquist, puede ocurrir el aliasing y hace que el espectro tome un espectro diferente al original.

Prueba del Teorema de Muestreo

La discusión anterior ya ha mostrado el teorema del muestreo de una manera informal e intuitiva que fácilmente podría refinarse en una prueba formal. Sin embargo, la prueba original del teorema de muestreo, que se dará aquí, proporciona la interesante observación de que las muestras de una señal con período\(T_s\) proporcionan coeficientes de serie de Fourier para el espectro de señal original encendido\(\left(-\pi / T_{s}, \pi / T_{s}\right)\).

Dejar\(x\) ser una señal de\(\left(-\pi / T_{s}, \pi / T_{s}\right)\) banda limitada y\(x_s\) ser sus muestras con periodo de muestreo\(T_s\). Podemos representar\(x\) en términos de su espectro\(X\) utilizando la transformada inversa de Fourier de tiempo continuo y el hecho de que\(x\) es de banda limitada. El resultado es

\[x(t)=\frac{1}{2 \pi} \int_{-\pi / T_{x}}^{\pi / T_{s}} X(\omega) e^{j \omega t} d \omega \nonumber \]

Esta representación de\(x\) puede entonces ser muestreada con período de muestreo\(T_s\) para producir

\[x_{s}(n)=x_{s}\left(n T_{s}\right)=\frac{1}{2 \pi} \int_{-\pi / T_{s}}^{\pi / T_{s}} X(\omega) e^{j \omega n T_{s}} d \omega \nonumber \]

Al notar que esto indica que\(x_s(n)\) es el\(n\) th coeficiente de serie de tiempo continuo de Fourier para\(X(\omega)\) en el intervalo\(\left(-\pi / T_{s}, \pi / T_{s}\right)\), se muestra que las muestras determinan el espectro original\(X(\omega)\) y, por extensión, la propia señal original.

Reconstrucción Perfecta

Otra forma de mostrar el teorema de muestreo es derivar la fórmula de reconstrucción que da la señal original\(\tilde{x}=x\) a partir de sus muestras\(x_s\) con periodo de muestreo\(T_s\), siempre que\(x\) sea de banda limitada a\(\left(-\pi / T_{s}, \pi / T_{s}\right)\). Esto se hace en el módulo sobre reconstrucción perfecta. No obstante, el resultado, conocido como la fórmula de reconstrucción de Whittaker-Shannon, se expondrá aquí. Si las condiciones requeridas se mantienen, entonces la reconstrucción perfecta viene dada por

\[x(t)=\sum_{n=-\infty}^{\infty} x_{s}(n) \operatorname{sinc}\left(t / T_{s}-n\right) \nonumber \]

donde la función sinc se define como

\[\operatorname{sinc}(t)=\frac{\sin (\pi t)}{\pi t}. \nonumber \]

A partir de esto, queda claro que el conjunto

\[\left\{\operatorname{sinc}\left(t / T_{s}-n\right) \: | \: n \in \mathbb{Z}\right\} \nonumber \]

forma una base ortogonal para el conjunto de señales de\(\left(-\pi / T_{s}, \pi / T_{s}\right)\) banda limitada, donde los coeficientes de una\(\left(-\pi / T_{s}, \pi / T_{s}\right)\) señal en esta base son sus muestras con periodo de muestreo\(T_s\).

Implicaciones prácticas

Procesamiento de tiempo discreto de señales de tiempo continuas

El teorema de muestreo de Nyquist-Shannon y la fórmula de reconstrucción Whittaker-Shannon permiten el procesamiento de tiempo discreto de señales de tiempo continuas. Debido a que cualquier filtro lineal invariante de tiempo realiza una multiplicación en el dominio de frecuencia, el resultado de aplicar un filtro lineal invariante de tiempo a una señal de banda limitada es una señal de salida con el mismo límite de banda. Dado que el muestreo de una señal de tiempo continuo de banda limitada por encima de la tasa de Nyquist produce una señal de tiempo discreta con un espectro de la misma forma que el espectro original, un filtro de tiempo discreto podría modificar el espectro de muestras y reconstruir perfectamente la salida para producir el mismo resultado que un filtro de tiempo continuo . Esto permite que el uso de la potencia informática digital y la flexibilidad se aprovechen también en el procesamiento continuo de señales de tiempo. Esto se describe más a fondo en el módulo final de este capítulo.

Psicoacústica

Las propiedades de la fisiología y la psicología humanas a menudo informan las elecciones de diseño en tecnologías destinadas a la interacción con las personas. Por ejemplo, los dispositivos digitales que se ocupan del sonido utilizan frecuencias de muestreo relacionadas con el rango de frecuencias de vocalizaciones humanas y el rango de frecuencia de la sensibilidad auditiva humana. Debido a que la mayoría de los sonidos en el habla humana concentran la mayor parte de su energía de señal entre 5 Hz y 4 kHz, la mayoría de los sistemas telefónicos descartan frecuencias superiores a 4 kHz y muestrean a una velocidad de 8 kHz. Descartar las frecuencias mayores o iguales a 4 kHz mediante el uso de un filtro anti-aliasing es importante para evitar el aliasing, lo que impactaría negativamente en la calidad del sonido de salida como se describe en un módulo posterior. Del mismo modo, la audición humana es sensible a frecuencias entre 20 Hz y 20 kHz. Por lo tanto, las frecuencias de muestreo para las formas de onda de audio generales colocadas en CD se eligieron para que fueran mayores a 40 kHz, y se descartó todo el contenido de frecuencia mayor o igual a algún nivel. El valor particular que se eligió, 44.1 kHz, se seleccionó por otras razones, pero el teorema de muestreo y el rango de audición humana proporcionaron un límite inferior para el rango de elecciones.

Resumen del teorema del muestreo

El Teorema de Muestreo de Nyquist-Shannon afirma que una señal de banda limitada a\(\left(-\pi / T_{s}, \pi / T_{s}\right)\) puede ser reconstruida exactamente a partir de sus muestras con período de muestreo\(T_s\). La fórmula de interpolación Whittaker-Shannon, que se describirá con mayor detalle en la sección sobre reconstrucción perfecta, proporciona la reconstrucción de la señal de tiempo continua\(\left(-\pi / T_{s}, \pi / T_{s}\right)\) limitada en banda única que muestrea a una señal de tiempo discreta dada con período de muestreo\(T_s\). Esto permite el procesamiento de tiempo discreto de señales de tiempo continuas, que tiene muchas aplicaciones potentes.