10.3: Reconstrucción de señal

Introducción

El proceso de muestreo produce una señal de tiempo discreta a partir de una señal de tiempo continua al examinar el valor de la señal de tiempo continua en puntos igualmente espaciados en el tiempo. La reconstrucción, también conocida como interpolación, intenta realizar un proceso opuesto que produce una señal de tiempo continua coincidiendo con los puntos de la señal de tiempo discreta. Debido a que el proceso de muestreo para conjuntos generales de señales no es invertible, existen numerosas reconstrucciones posibles a partir de una señal de tiempo discreta dada, cada una de las cuales muestrearía esa señal a la velocidad de muestreo apropiada. Este módulo introducirá algunos de estos esquemas de reconstrucción.

Reconstrucción

Proceso de Reconstrucción

El proceso de reconstrucción, también conocido comúnmente como interpolación, produce una señal de tiempo continua que muestrearía a una señal de tiempo discreta dada a una frecuencia de muestreo específica. La reconstrucción se puede entender matemáticamente generando primero un tren de impulsos de tiempo continuo

\[x_{i m p}(t)=\sum_{n=-\infty}^{\infty} x_{s}(n) \delta\left(t-n T_{s}\right) \nonumber \]

a partir de la señal muestreada\(x_s\) con periodo de muestreo\(T_s\) y luego aplicar un filtro de paso bajo\(G\) que satisfaga ciertas condiciones para producir una señal de salida\(\tilde{x}\). Si\(G\) tiene respuesta de impulso\(g\), entonces el resultado del proceso de reconstrucción, ilustrado en la Figura\(\PageIndex{1}\), viene dado por el siguiente cálculo, cuya ecuación final se utiliza para realizar la reconstrucción en la práctica.

\ [\ begin {align}
\ Widetilde {x} (t) &=\ izquierda (x_ {i m p} * g\ derecha) (t)\ nonumber\\
&=\ int_ {-\ infty} ^ {\ infty} x_ {i m p} (\ tau) g (t-\ tau) d\ tau\ nonumber\\
&=\ int_ {-\ infty} ^ {\ infty}\ suma_ {n=-\ infty} ^ {\ infty} x_ {s} (n)\ delta\ izquierda (\ tau-n T_ {s}\ derecha) g (t-\ tau) d\ tau\ nonumber\\
&=\ suma_ {n=-\ infty} ^ {\ infty} x_ {s} (n)\ int_ {-\ infty} ^ {\ infty}\ delta\ izquierda (\ tau-n T_ {s}\ derecha) g (t-\ tau) d\ tau\ nonumber\\
&=\ sum_ {n=-\ infty} ^ {\ infty} x_ {s} (n) g\ izquierda (t-n T_ {s}\ derecha)
\ end {align}\ nonumber\]

Figura\(\PageIndex{1}\): Diagrama de bloques del proceso de reconstrucción para un filtro de paso bajo dado\(G\).

Filtros de Reconstrucción

Para garantizar que la señal reconstruida\(\tilde{x}\) muestree a la señal de tiempo discreta a\(x_s\) partir de la cual fue reconstruida utilizando el periodo de muestreo\(T_s\), el filtro de paso bajo\(G\) debe cumplir ciertas condiciones. Estos se pueden expresar bien en el dominio del tiempo en términos de una condición sobre la respuesta\(g\) de impulso del filtro de paso bajo\(G\). La condición suficiente para ser una reconstrucción filtros que vamos a requerir es que, para todos\(n \in \mathbb{Z}\),

\ [g\ left (n T_ {s}\ right) =\ left\ {\ begin {array} {ll}
1 & n=0\\
0 & n\ neq 0
\ end {array} =\ delta (n)\ right. \ nonumber\]

Esto significa que gg muestreado a una velocidad\(T_s\) produce una señal de impulso de unidad de tiempo discreta. Por lo tanto, se deduce que el muestreo\(\tilde{x}\) con periodo de muestreo\(T_s\) da como resultado

\ [\ begin {align}
\ Widetilde {x}\ izquierda (n T_ {s}\ derecha) &=\ suma_ {m=-\ infty} ^ {\ infty} x_ {s} (m) g\ izquierda (n T_ {s} -m T_ {s}\ derecha)\ nonumber\\
&=\ sum_ {m=-\ infty} ^ {\ infty} x_ {s} (m) g\ izquierda ((n-m) T_ {s}\ derecha)\ nonumber\\
&=\ suma_ {m=-\ infty} ^ {\ infty} x_ {s} (m)\ delta (n-m)\ nonumber\\
&=x_ {s} (n),
\ end {align}\ nonumber\]

que es el resultado deseado para los filtros de reconstrucción.

Splines de base cardinal

Dado que hay muchas señales de tiempo continuas que muestrean a una señal de tiempo discreta dada, se requieren restricciones adicionales para identificar una en particular de estas. Por ejemplo, podríamos requerir nuestra reconstrucción para producir una spline de cierto grado, que es una señal descrita en partes por partes por polinomios que no excedan ese grado. Adicionalmente, podríamos querer garantizar que la función y cierto número de sus derivadas son continuas.

Esto se puede lograr restringiendo el resultado a la extensión de conjuntos de ciertas splines, llamadas splines base o B-splines. Específicamente, si se requiere una spline de grado\(n\) th con derivadas continuas hasta al menos orden\(n−1\), entonces la función deseada para un determinado\(T_s\) pertenece al lapso de\(\left\{B_{n}\left(t / T_{s}-k\right) \: | \: k \in \mathbb{Z}\right\}\) donde

\[B_{n}=B_{0} * B_{n-1} \nonumber \]

para\(n≥1\) y

\ [B_ {0} (t) =\ left\ {\ begin {array} {cc}
1 & -1/2<t<1/2\\
0 &\ text {de lo contrario}
\ end {array}\ right. \ nonumber\]

Figura\(\PageIndex{2}\): Las splines de base\(B_n\) se muestran en las gráficas anteriores. Tenga en cuenta que, a excepción de las funciones de orden 0 y orden 1, estas funciones no satisfacen las condiciones para ser filtros de reconstrucción. También observe que a medida que aumenta el orden, las funciones se acercan a la función gaussiana, que es exactamente\(B_{\infty}\).

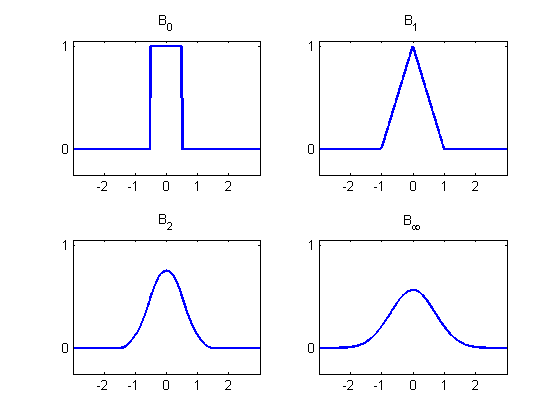
Sin embargo, las splines base\(B_n\) no satisfacen las condiciones para ser un filtro de reconstrucción\(n≥2\) como se muestra en la Figura\(\PageIndex{2}\). Aún así, los\(B_n\) son útiles para definir las splines de base cardinal, que sí satisfacen las condiciones para ser filtros de reconstrucción. Si dejamos\(b_n\) ser las muestras de\(B_n\) en los enteros, resulta que\(b_n\) tiene una inversa\(b^{−1}_n\) con respecto a la operación de convolución para cada uno\(n\). Esto es para decir eso\(b_{n}^{-1} * b_{n}=\delta\). La spline de base cardinal de orden nn para reconstrucción con periodo de muestreo\(T_s\) se define como

\[\eta_{n}(t)=\sum_{k=-\infty}^{\infty} b_{n}^{-1}(k) B_{n}\left(t / T_{s}-k\right). \nonumber \]

Para confirmar que esto satisface la condición de ser un filtro de reconstrucción, tenga en cuenta que

\[\eta_{n}\left(m T_{s}\right)=\sum_{k=-\infty}^{\infty} b_{n}^{-1}(k) B_{n}(m-k)=\left(b_{n}^{-1} * b_{n}\right)(m)=\delta(m). \nonumber \]

Por lo tanto,\(\eta_n\) es un filtro de reconstrucción válido. Dado que\(\eta_n\) es una spline de\(n\) th grado con derivadas continuas por orden\(n−1\), el resultado de la reconstrucción será una spline de\(n\) th grado con derivadas continuas hasta el orden\(n−1\).

Figura\(\PageIndex{3}\): Las gráficas anteriores muestran las funciones de spline de base cardinal\(\eta_0\)\(\eta_1\),,\(\eta_2\), y\(\eta_{\infty}\). Tenga en cuenta que las funciones satisfacen las condiciones para ser filtros de reconstrucción. También, observe que a medida que aumenta el orden, las splines de base cardinal se aproximan a la función sinc, que es exactamente\(\eta_{\infty}\). Adicionalmente, estos filtros son acausales.

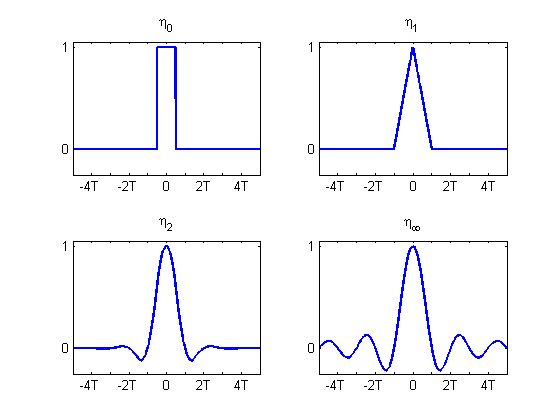
El filtro de paso bajo con respuesta de impulso igual a la spline\(\eta_0\) de base cardinal de orden 0 es uno de los ejemplos más simples de un filtro de reconstrucción. Simplemente extiende el valor de la señal de tiempo discreta durante la mitad del período de muestreo a cada lado de cada muestra, produciendo una reconstrucción constante por partes. Así, el resultado es discontinuo para todas las señales de tiempo discretas no constantes.

Asimismo, el filtro de paso bajo con respuesta de impulso igual a la spline\(\eta_1\) de base cardinal de orden 1 es otro de los ejemplos más simples de un filtro de reconstrucción. Simplemente une las muestras adyacentes con una línea recta, produciendo una reconstrucción lineal por tramos. De esta manera, la reconstrucción es continua para todas las señales de tiempo discretas posibles. Sin embargo, a menos que las muestras sean colineales, el resultado tiene primeras derivadas discontinuas.

En general, se pueden hacer declaraciones similares para filtros de paso bajo con respuestas de impulso iguales a splines de base cardinal de cualquier orden. Usando la spline de base cardinal de orden\(n\) th\(\eta_n\), el resultado es un polinomio nn de grado por tramos. Además, tiene derivadas continuas hasta por lo menos orden\(n−1\). Sin embargo, a menos que todas las muestras sean puntos en un polinomio de grado como máximo\(n\), la derivada del orden nn será discontinua.

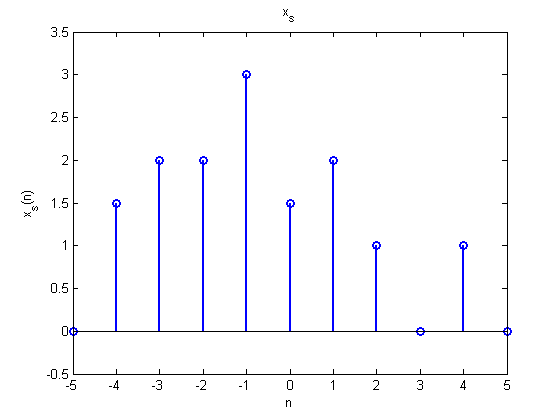
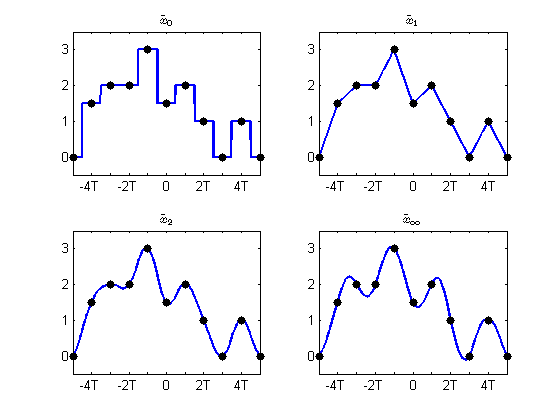
Las reconstrucciones de la señal de tiempo discreta dada en la Figura\(\PageIndex{4}\) usando varios de estos filtros se muestran en la Figura\(\PageIndex{5}\). A medida que aumenta el orden de la spline de base cardinal, observe que la reconstrucción se acerca a la del orden infinito cardinal spline\(\eta_{\infty}\), la función sinc. Como se mostrará en la siguiente sección sobre reconstrucción perfecta, los filtros con respuesta de impulso igual a la función sinc juegan un papel especialmente importante en el procesamiento de señales.

Figura\(\PageIndex{4}\): La gráfica anterior muestra una función de tiempo discreta de ejemplo. Esta función de tiempo discreta se reconstruirá usando el período de muestreo\(T_s\) usando varias splines de base cardinal en la Figura\(\PageIndex{5}\).

Figura\(\PageIndex{5}\): Las gráficas anteriores muestran interpolaciones de la señal de tiempo discreta dada en la Figura\(\PageIndex{4}\) usando filtros de paso bajo con respuestas de impulso dadas por las splines de base cardinal mostradas en la Figura\(\PageIndex{3}\). Note que las interpolaciones se vuelven cada vez más suaves y se acercan a la interpolación sinc a medida que aumenta el orden.

Resumen de Reconstrucción

La reconstrucción de una señal de tiempo continua a partir de una señal de tiempo discreta se puede lograr a través de varios esquemas. Sin embargo, es importante señalar que la reconstrucción no es la inversa del muestreo y solo produce una posible señal de tiempo continua que muestrea a una señal de tiempo discreta dada. Como se cubre en el módulo posterior, la reconstrucción perfecta de una señal de tiempo continuo de banda limitada a partir de su versión muestreada es posible utilizando la fórmula de reconstrucción Whittaker-Shannon, que hace uso del filtro de paso bajo ideal y su respuesta de impulso de función sinc, si la frecuencia de muestreo es suficiente alto.