13.2: La Transformada Rápida de Fourier (FFT)
- Page ID
- 86204
Introducción
La Transformada Rápida de Fourier (FFT) es un algoritmo eficiente O (nLogN) para calcular DFT La FFT explota simetrías en la\(W\) matriz para adoptar un enfoque de “dividir y conquistar”. Primero discutiremos derivar el algoritmo FFT real, algunas de sus implicaciones para el DFT, y una comparación de velocidad para conducir a casa la importancia de este poderoso algoritmo.
Derivando la FFT
Para derivar la FFT, asumimos que la duración de la señal es una potencia de dos:\(N=2^l\). Considere lo que sucede con los elementos pares e impares de la secuencia en el cálculo de DFT.
\[\begin{align}S(k) &=s(0)+s(2) e^{(-j) \frac{2 \pi 2 k}{N}}+\ldots+s(N-2) e^{(-j) \frac{2 \pi(N-2) k}{N}}+s(1) e^{(-j) \frac{2 \pi k}{N}}+s(3) e^{(-j) \frac{2 \pi \times (2+1) k}{N}}+\ldots+s(N-1) e^{(-j) \frac{2 \pi(N-2+1) k}{N}} \nonumber \\ &=s(0)+s(2)e^{(-j)\frac{2\pi k}{\frac{N}{2}}} + \ldots + s(N-2)e^{(-j) \frac{2 \pi\left(\frac{N}{2}-1\right) k}{\frac{N}{2}}} +\left( s(1)+s(3) e^{(-j) \frac{2 \pi k}{\frac{N}{2}}}+\dots+s(N-1) e^{(-j) \frac{2 \pi\left(\frac{N}{2}-1\right) k}{\frac{N}{2}}}\right) e^{\frac{-(j 2 \pi k)}{N}} \end{align} \nonumber \]
Cada término entre corchetes tiene la forma de un DFT de\(\frac{N}{2}\) longitud. El primero es un DFT de los elementos pares y el segundo de los elementos impares. El primer DFT se combina con el segundo multiplicado por el exponencial complejo\(e^{\frac{-(j 2\pi k)}{N}}\). Las transformaciones de media longitud se evalúan cada una en índices de frecuencia\(k \in\{0, \ldots, N-1\}\). Normalmente, el número de índices de frecuencia en un cálculo de DFT oscila entre cero y la longitud de transformación menos uno. La ventaja computacional de la FFT proviene del reconocimiento de la naturaleza periódica de la transformada discreta de Fourier. La FFT simplemente reutiliza los cálculos realizados en las transformaciones de media longitud y los combina a través de adiciones y la multiplicación por\(e^{\frac{-(j 2 \pi k)}{N}}\), que no es periódica sobre\(\frac{N}{2}\), para reescribir el Length-N DFT. La figura\(\PageIndex{1}\) ilustra esta descomposición. Tal como está, ahora calculamos dos\(\frac{N}{2}\) transformaciones de longitud (complejidad\(2 O\left(\frac{N^{2}}{4}\right)\)), multiplicamos una de ellas por la exponencial compleja (complejidad\(O(N)\)) y agregamos los resultados (complejidad\(O(N)\)). En este punto, la complejidad total aún está dominada por los cálculos de DFT de longitud media, pero el coeficiente de proporcionalidad se ha reducido.
Ahora por la diversión. Porque\(N=2^l\), cada una de las transformaciones de media longitud se puede reducir a dos transformadas de un cuarto de longitud, cada una de estas a dos transformadas de octava longitud, etc. Esta descomposición continúa hasta que nos quedamos con transformaciones de longitud-2. Esta transformación es bastante simple, involucrando solo adiciones. Así, la primera etapa de la FFT tiene transformaciones de\(\frac{N}{2}\) longitud-2 (ver la parte inferior de la Figura\(\PageIndex{1}\)). Los pares de estas transformaciones se combinan sumando una a la otra multiplicada por un exponencial complejo. Cada par requiere 4 adiciones y 4 multiplicaciones, dando un número total de cómputos igualados\(8\frac{N}{4}=\frac{N}{2}\). Este número de cálculos no cambia de etapa a etapa. Debido a que el número de etapas, el número de veces que la longitud se puede dividir por dos, es igual\(\log_2 N\), la complejidad de la FFT es\(O(N \log N)\).
Descomposición DFT de longitud 8
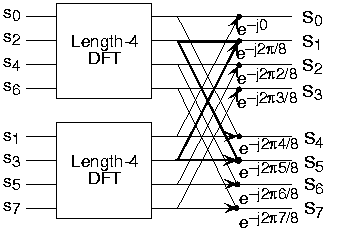 a)
a)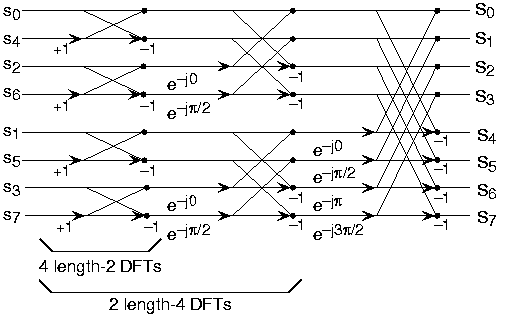 b)
b)Hacer un ejemplo hará que el ahorro computacional sea más obvio. Veamos los detalles de un DFT de longitud 8. Como se muestra en la Figura\(\PageIndex{1}\), primero descomponemos el DFT en dos DFT de longitud 4, con las salidas sumadas y restadas juntas en pares. Considerando Figura\(\PageIndex{1}\) como el índice de frecuencia va de 0 a 7, reciclamos valores de los DFT de longitud-4 al cálculo final debido a la periodicidad de la salida de DFT. Al examinar cómo se recopilan los pares de salidas, creamos el elemento computacional básico conocido como mariposa (Figura\(\PageIndex{2}\)).

Al considerar juntos los cálculos que involucran frecuencias de salida comunes de las dos DFT de media longitud, vemos que las dos multiplica complejas están relacionadas entre sí, y podemos reducir aún más nuestro trabajo computacional. Al descomponer aún más las DFT de longitud 4 en dos DFT de longitud 2 y combinar sus salidas, llegamos al diagrama que resume la transformada rápida de Fourier de longitud 8 (Figura\(\PageIndex{1}\)). Si bien la mayoría de las multiplicidades complejas son bastante simples (multiplicando por\(e^{-(j\pi)}\) medios negando partes reales e imaginarias), vamos a contarlas con el propósito de evaluar la complejidad como multiplicaciones complejas completas. Tenemos\(2N=16\) multiplicaciones y adiciones\(\frac{N}{2}=4\) complejas para cada etapa y\(\log_2 N=3\) etapas, haciendo que el número de cálculos básicos\(\frac{3N}{2} \log_2 N\) como se predijo.
Ejercicio\(\PageIndex{1}\)
Tenga en cuenta que el orden de la secuencia de entrada en las dos partes de Figura\(\PageIndex{1}\) no es exactamente el mismo. ¿Por qué no? ¿Cómo se determina el orden?
- Responder
-
El panel superior no ha utilizado el algoritmo FFT para calcular los DFT de longitud 4 mientras que el inferior tiene. El orden está determinado por el algoritmo.
FFT y DFT
Ahora tenemos una forma de calcular el espectro para una señal arbitraria: La Transformada Discreta de Fourier (DFT) calcula el espectro a frecuencias\(N\) igualmente espaciadas a partir de una\(N\) secuencia de longitud. Un problema que nunca surge en el “cálculo” analógico, como el que realiza un circuito, es cuánto trabajo se necesita para realizar la operación de procesamiento de señal como el filtrado. En el cálculo, esta consideración se traduce en el número de pasos computacionales básicos requeridos para realizar el procesamiento necesario. El número de pasos, conocido como la complejidad, se vuelve equivalente a cuánto tiempo lleva el cálculo (cuánto tiempo debemos esperar una respuesta). La complejidad no está tanto ligada a computadoras o lenguajes de programación específicos sino a cuántos pasos se requieren en cualquier computadora. Así, la complejidad declarada de un procedimiento dice que el tiempo empleado será proporcional a alguna función de la cantidad de datos utilizados en el cómputo y la cantidad demandada.
Por ejemplo, considere la fórmula para la transformada discreta de Fourier. Para cada frecuencia que elegimos, debemos multiplicar cada valor de señal por un número complejo y sumar los resultados. Para una señal de valor real, cada multiplicación compleja en tiempo real requiere dos multiplicaciones reales, lo que significa que tenemos\(2N\) multiplicaciones que realizar. Para sumar los resultados, debemos mantener separadas las partes real e imaginaria. Agregar\(N\) números requiere\(N−1\) adiciones. En consecuencia, cada frecuencia requiere pasos computacionales\(2N+2(N−1)=4N−2\) básicos. Como tenemos\(N\) frecuencias, el número total de cómputos es\(N(4N−2)\).
En los cálculos de complejidad, solo nos preocupamos por lo que sucede a medida que aumentan las longitudes de los datos, y tomamos el\(4N^2\) término dominante, aquí el término, como reflejo de cuánto trabajo implica hacer el cálculo. Como las constantes multiplicativas no importan ya que estamos haciendo una evaluación “proporcional a”, encontramos que la DFT es un procedimiento\(O(N^2)\) computacional. Esta notación se lee “orden\(N\) -cuadrado”. Así, si duplicamos la longitud de los datos, esperaríamos que el tiempo de cómputo se cuadruplicara aproximadamente.
Ejercicio\(\PageIndex{2}\)
Al hacer la evaluación de complejidad para el DFT, asumimos que los datos eran reales. Surgen tres preguntas. En primer lugar, los espectros de tales señales tienen simetría conjugada, lo que significa que los componentes de frecuencia negativa (\(k=\left[\frac{N}{2}+1, \ldots, N+1\right]\)en la DFT) pueden calcularse a partir de los componentes de frecuencia positiva correspondientes. ¿Esta simetría cambia la complejidad de la DFT?
En segundo lugar, supongamos que los datos son de valor complejo; ¿cuál es la complejidad de la DFT ahora?
Por último, una pregunta menos importante pero interesante es suponer que queremos valores de\(K\) frecuencia en lugar de\(N\); ahora ¿cuál es la complejidad?
- Responder
-
Cuando la señal es de valor real, es posible que solo necesitemos la mitad de los valores espectrales, pero la complejidad permanece sin cambios. Si los datos son de valor complejo, lo que exige retener todos los valores de frecuencia, la complejidad vuelve a ser la misma. Cuando solo se necesitan\(K\) frecuencias, la complejidad es\(O(KN)\).
Comparación de velocidad
¿Cuánto mejor es\(O(N \log N)\) que\(O( N^2)\)?

| \(N\) | \(10\) | \(100\) | \(1000\) | \(10^6\) | \(10^9\) |
|---|---|---|---|---|---|
| \ (N\)” class="lt-eng-22922">\(N^2\) | \ (10\)” class="lt-eng-22922">\(100\) | \ (100\)” class="lt-eng-22922">\(10^4\) | \ (1000\)” class="lt-eng-22922">\(10^6\) | \ (10^6\)” class="lt-eng-22922">\(10^{12}\) | \ (10^9\)” class="lt-eng-22922">\(10^{18}\) |
| \ (N\)” class="lt-eng-22922">\(N \log N\) | \ (10\)” class="lt-eng-22922">\(1\) | \ (100\)” class="lt-eng-22922">\(200\) | \ (1000\)” class="lt-eng-22922">\(3000\) | \ (10^6\)” class="lt-eng-22922">\(6 \times 10^6\) | \ (10^9\)” class="lt-eng-22922">\(9 \times 10^9\) |
Supongamos que tiene una máquina 1 MFLOP (un millón de operaciones de “punto flotante” por segundo). Dejar\(N\) =1 millones=\(10^6\).
Un\(O( N^2)\) algoritmo tarda\(10^{12}\) Flors →\(10^6\) segundos 11.5 días.
Un\(O( N \log N)\) algoritmo tarda\(6 \times 10^6\) Flors → 6 segundos.
Nota
N = 1 millón no es irrazonable.
Ejemplo\(\PageIndex{1}\)
La cámara digital de 3 megapíxeles escupe\(3 \times 10^6\) números para cada imagen. Entonces para dos secuencias\(N\) puntuales\(f[n]\) y\(h[n]\). Si\(f[n]⊛h[n]\) computa directamente:\(O( N^2)\) operaciones.
tomando FFT —\(O(N \log N)\)
multiplicando FFT —\(O(N)\)
FFT inversos —\(O(N \log N)\).
la complejidad total es\(O(N \log N)\).
Conclusión
Se han descubierto otros algoritmos “rápidos”, la mayoría de los cuales hacen uso de cuántos factores comunes tiene la longitud de transformación N. En teoría de números, el número de factores primos que tiene un entero dado mide qué tan compuesto es. Los números 16 y 81 son altamente compuestos (iguales\(2^4\) y\(3^4\) respectivamente), el número 18 lo es menos (\(2^1 3^2\)) y 17 no en absoluto (es primo). En más de treinta años de desarrollo del algoritmo de transformada de Fourier, el algoritmo original de Cooley-Tukey es, de lejos, el más utilizado. Es tan eficiente desde el punto de vista computacional que las longitudes de transformación de potencia de dos se utilizan con frecuencia independientemente de cuál sea la longitud real de los datos. Incluso está bien establecido que la FFT, junto con la computadora digital, fueron casi completamente responsables de la “explosión” de DSP en los años 60.


