13.4: Detector de filtro emparejado
- Page ID
- 86207
Introducción
Muchas aplicaciones en el procesamiento de señales, procesamiento de imágenes y más allá implican determinar la presencia y ubicación de una señal objetivo dentro de alguna otra señal. Un sistema de radar, por ejemplo, busca copias de un pulso de radar transmitido con el fin de determinar la presencia y distancia a objetos reflectantes como edificios o aeronaves. Un sistema de comunicación busca copias de formas de onda que representan 0s y 1s digitales para recibir un mensaje.
Dos herramientas matemáticas clave que contribuyen a estas aplicaciones son los productos internos y la desigualdad Cauchy-Schwarz. Como se muestra en el módulo sobre la desigualdad Cauchy-Schwarz, la expresión\(\left|\left\langle\frac{x}{|| x||}, \frac{y}{\|y\|}\right\rangle\right|\) alcanza su límite superior, que es 1, cuando\(y=ax\) para algún escalar\(a\) en un campo real o complejo. El límite inferior, que es 0, se alcanza cuando\(x\) y\(y\) son ortogonales. En la intuición informal, esto significa que la expresión se maximiza cuando los vectores\(x\) y\(y\) tienen la misma forma o patrón y minimizada cuando\(x\) y\(y\) son muy diferentes. Un par de vectores con formas o patrones similares pero desiguales producirán un valor relativamente grande de la expresión menor que 1, y un par de vectores con formas o patrones muy diferentes pero no ortogonales producirán valores relativamente pequeños de la expresión mayores que 0. Así, la expresión anterior lleva consigo una noción del grado en que dos señales son “iguales”, la magnitud de la correlación normalizada entre las señales en el caso de los productos internos estándar.
Este concepto puede ser sumamente útil. Por ejemplo, consideremos una situación en la que deseamos determinar qué señal, si la hay, de un conjunto\(X\) de señales se parece más a una señal particular\(y\). Para lograr esto, podríamos evaluar la expresión anterior para cada señal\(x \in X\), eligiendo la que dé como resultado máximos siempre que esos máximos estén por encima de algún umbral de “semejanza”. Esta es la idea detrás del detector de filtro emparejado, que compara un conjunto de señales contra una señal objetivo usando la expresión anterior para determinar cuál es la más parecida a la señal objetivo.
Teoría del detector de filtro emparejado
Comparación de señales
La variante más simple del esquema de detector de filtro emparejado sería encontrar la señal miembro en un conjunto\(X\) de señales que coincidan más estrechamente con una señal objetivo\(y\). Así, para cada uno que\(x \in X\) deseamos evaluar
\[m(x, y)=\left|\left\langle\frac{x}{|| x||}, \frac{y}{\|y\|}\right\rangle\right| \nonumber \]
con el fin de comparar cada miembro\(X\) de con la señal objetivo\(y\). Dado que se desea el miembro del\(X\) que más\(y\) se aproxime a la señal objetivo, en última instancia deseamos evaluar
\[x_{m}=\operatorname{argmax} _{x \in X}\left|\left\langle\frac{x}{\|x\|}, \frac{y}{\|y\|}\right\rangle\right| \nonumber \]
Tenga en cuenta que la señal objetivo no necesita normalizarse técnicamente para producir un máximo, sino que da la propiedad deseable a la que\(m(x,y)\) se limita\([0,1]\).
El elemento\(x_{m} \in X\) que produce el valor máximo de no\(m(x,y)\) es necesariamente único, por lo que puede haber más de una señal coincidente en\(X\). Adicionalmente, la señal\(x_m \in X\) que produce el valor máximo de\(m(x,y)\) puede no producir un valor muy grande de\(m(x,y)\) y, por lo tanto, no ser muy parecida a la señal objetivo\(y\). Por lo tanto, otro esquema de filtro coincidente podría identificar el argumento que produce el máximo pero solo por encima de un cierto umbral, no devolviendo señales coincidentes\(X\) si el máximo está por debajo del umbral. También puede haber una señal\(x \in X\) que produzca un gran valor de\(m(x,y)\) y por lo tanto tenga un alto grado de “semejanza” a\(y\) pero no produzca el valor máximo de\(m(x,y)\). Por lo tanto, otro esquema de filtro coincidente podría identificar todas las señales en la\(X\) producción de máximos locales que están por encima de un cierto umbral.
Ejemplo\(\PageIndex{1}\)
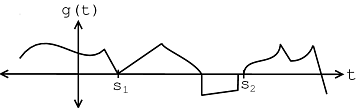
Por ejemplo, considere la señal objetivo dada en la Figura\(\PageIndex{1}\) y el conjunto de dos señales dadas en la Figura\(\PageIndex{2}\). Por inspección, es claro que la señal\(g_2\) se parece más a la señal objetivo\(f\). Sin embargo, para llegar a esa conclusión matemáticamente, utilizamos el detector de filtro emparejado con el producto\(L_2\) interno. Si realmente tuviéramos que hacer los cálculos necesarios, primero normalizaríamos cada señal y luego calcularíamos los productos internos necesarios para comparar las señales\(X\) con la señal objetivo\(f\). Notaríamos que el valor absoluto del producto interno para\(g_2\) con\(f\) cuando se normaliza es mayor que el valor absoluto del producto interno de\(g_1\) con\(f\) cuando se normaliza, expresado matemáticamente como
\[g_{2}=\operatorname{arg max}_{x \in\left\{g_{1}, g_{2}\right\}}\left|\left\langle\frac{x}{\| x||}, \frac{f}{\|f\|}\right\rangle\right| \nonumber \]
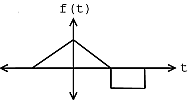
Señales de Candidatos
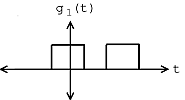 (a)
(a)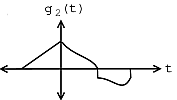 b)
b)Detección de Patrones
Un esquema de detector de filtro emparejado algo más involucrado implicaría intentar hacer coincidir una señal\(y=f\) de tiempo limitado objetivo con un conjunto de versiones con desplazamiento de tiempo y en ventana de una única señal\(X=\left\{w S_{t} g \mid t \in \mathbb{R}\right\}\) indexada por\(\mathbb{R}\). La función de ventana viene dada por\(w(t)=u\left(t-t_{1}\right)-u\left(t-t_{2}\right)\) dónde\(\left[t_{1}, t_{2}\right]\) está el intervalo al que\(f\) está limitado en el tiempo. Este esquema podría usarse para encontrar porciones de\(g\) que tengan la misma forma que\(f\). Si el valor absoluto del producto interno de las versiones normalizadas de\(f\) y\(w S_{t} g\) es grande, que es el valor absoluto de la correlación normalizada para los productos internos estándar, entonces\(g\) tiene un alto grado de “semejanza” a\(f\) en el intervalo al que\(f\) es el tiempo limitado pero desplazado a la izquierda por\(t\). Por supuesto, si no\(f\) está limitado en el tiempo, significa que toda la señal tiene un alto grado de “semejanza” a la\(f\) izquierda desplazada por\(t\).
Por lo tanto, para determinar las ubicaciones más probables de una señal con la misma forma que la señal objetivo\(f\) en una señal,\(g\) deseamos calcular
\[t_{m}=\operatorname{argmax}_{t \in \mathbb{R}} \mid\left\langle\frac{f}{\|f\|}, \frac{w S_{t} g}{\left\|w S_{t} g\right\|}\right\rangle \nonumber \]
para proporcionar el turno deseado. Suponiendo que el espacio interno del producto examinado es\(L_2\)\(\mathbb{R}\) ((resultados similares se mantienen para\(L_{2}(\mathbb{R}[a, b))\)\(l_2(\mathbb{Z})\), y\(l_{2}(\mathbb{Z}[a, b))\)), esto produce
\[t_{m}=\operatorname{argmax}_{t \in \mathbb{R}}\left|\frac{1}{\|f\|\left\|w S_{t} g\right\|} \int_{-\infty}^{\infty} f(\tau) w(\tau) \overline{g(\tau-t)} d \tau\right| \nonumber \]
Desde\(f\) y\(w\) están limitados en el tiempo al mismo intervalo
\[t_{m}=\operatorname{argmax}_{t \in \mathbb{R}}\left|\frac{1}{\|f\|\left\|w S_{t} g\right\|} \int_{t_{1}}^{t_{2}} f(\tau) \overline{g(\tau-t)} d \tau\right| \nonumber \]
Haciendo la sustitución\(h(t)=\overline{g(-t)}\),
\[t_{m}=\operatorname{argmax}_{t \in \mathbb{R}}\left|\frac{1}{\|f\|\left\|w S_{t} g\right\|} \int_{t_{1}}^{t_{2}} f(\tau) h(t-\tau) d \tau\right|. \nonumber \]
Observando que esta expresión contiene una operación de convolución
\[t_{m}=\operatorname{argmax}_{t \in \mathbb{R}}\left|\frac{(f * h)(t)}{\|f\|\left\|w S_{t} g\right\|}\right| \nonumber \]
donde\(h\) es el conjugado de la versión de tiempo invertido de\(g\) definido por\(h(t)=\overline{g(-t)}\).
En el caso especial en el que la señal objetivo no\(f\) esté limitada en el tiempo,\(w\) tiene valor unitario en toda la línea real. Así, la norma puede ser evaluada como\(\left\|w S_{t} g\right\|=\left\|S_{t} g\right\|=\|g\|=\|h\|\). Por lo tanto, la función se reduce a\(t_{m}=\operatorname{argmax}_{t \in \mathbb{R}} \frac{\left(f * h\right)(t)}{\|f\|\left\|h\right\|}\) donde\(h(t)=\overline{g(-t)}\). La función\(f * g=\frac{\left(f * h\right)(t)}{\|f\|\left\| h\right\|}\) se conoce como la correlación cruzada normalizada de\(f\) y\(g\).
Por lo tanto, este esquema de filtro coincidente se puede implementar como una convolución. Por lo tanto, puede ser conveniente implementarlo en el dominio de la frecuencia. Resultados similares se mantienen para los\(L_{2}(\mathbb{R}[a, b))\),\(l_{2}(\mathbb{Z})\), y\(l_{2}(\mathbb{Z}[a, b])\) espacios. Es especialmente útil implementar\(l_{2}(\mathbb{Z}[a, b])\) los casos en el dominio de la frecuencia ya que la potencia del algoritmo de Transformada Rápida de Fourier se puede aprovechar para realizar rápidamente los cálculos en un programa de computadora. En los\(l_{2}(\mathbb{Z}[a, b])\) casos\(L_{2}(\mathbb{R}[a, b))\) y, se debe tener cuidado de poner a cero la señal si no se desean efectos envolventes. Resultados similares también se mantienen para espacios en intervalos dimensionales más altos con los mismos productos internos.
Por supuesto, no hay necesariamente exactamente una instancia de una señal objetivo en una señal dada. Podría haber una instancia, más de una instancia, o ninguna instancia de una señal objetivo. Por lo tanto, a menudo es más práctico identificar todos los turnos correspondientes a máximos locales que estén por encima de un cierto umbral.
Ejemplo\(\PageIndex{2}\)
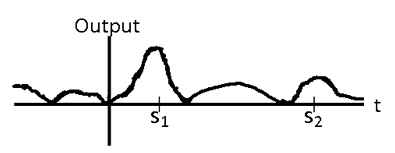
La señal en la Figura\(\PageIndex{4}\) contiene una instancia de la señal de plantilla vista en la Figura\(\PageIndex{3}\) comenzando en el tiempo\(t=s_1\) como se muestra en la gráfica de la Figura\(\PageIndex{5}\). Por lo tanto,
\[s_{1}=\operatorname{argmax}_{t \in \mathbb{R}}\left|\left\langle\frac{f}{\|f\|}, \frac{w S_{t} g}{\left\|w S_{t} g\right\|}\right\rangle\right|. \nonumber \]
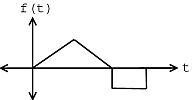
Aplicaciones prácticas
Detección de imágenes
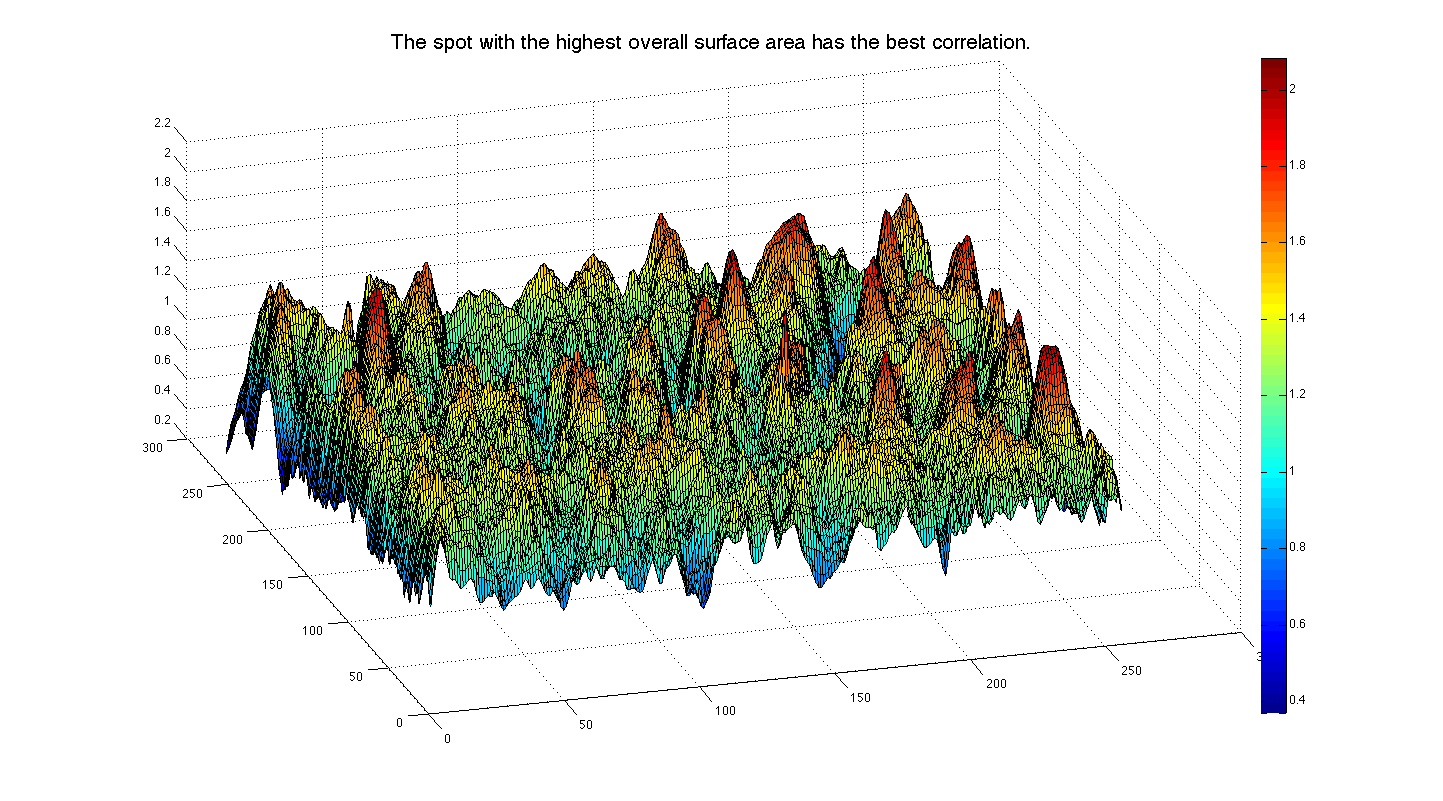
El filtrado coincidente se utiliza en el procesamiento de imágenes para detectar una imagen de plantilla dentro de una imagen de referencia. Esto tiene aplicaciones de palabras reales en la verificación de huellas dactilares por seguridad o en la verificación de la foto de alguien. Como ejemplo sencillo, podemos recurrir al siempre popular “¿Dónde está Waldo?” libros (¡conocidos como Wally en el Reino Unido!) , donde el lector tiene la tarea de encontrar el rostro específico de Waldo/Wally en un confuso trasfondo plagado de parecidos! Si se nos da la cabeza de plantilla y una imagen de referencia, podemos ejecutar una convolución bidimensional de la imagen de plantilla a través de la imagen de referencia para obtener un mapa de convolución tridimensional\(\PageIndex{6(a)}\), Figura, donde la altura del mapa de convolución está determinada por el grado de correlación, siendo mayor más correlacionados. Encontrar nuestro objetivo se convierte entonces en una cuestión de determinar el punto donde la superficie local es más alta. El proceso se demuestra en la Figura\(\PageIndex{6(b)}\). En el campo del procesamiento de imágenes, este proceso basado en filtros coincidentes se conoce como coincidencia de plantillas.
 (a)
(a)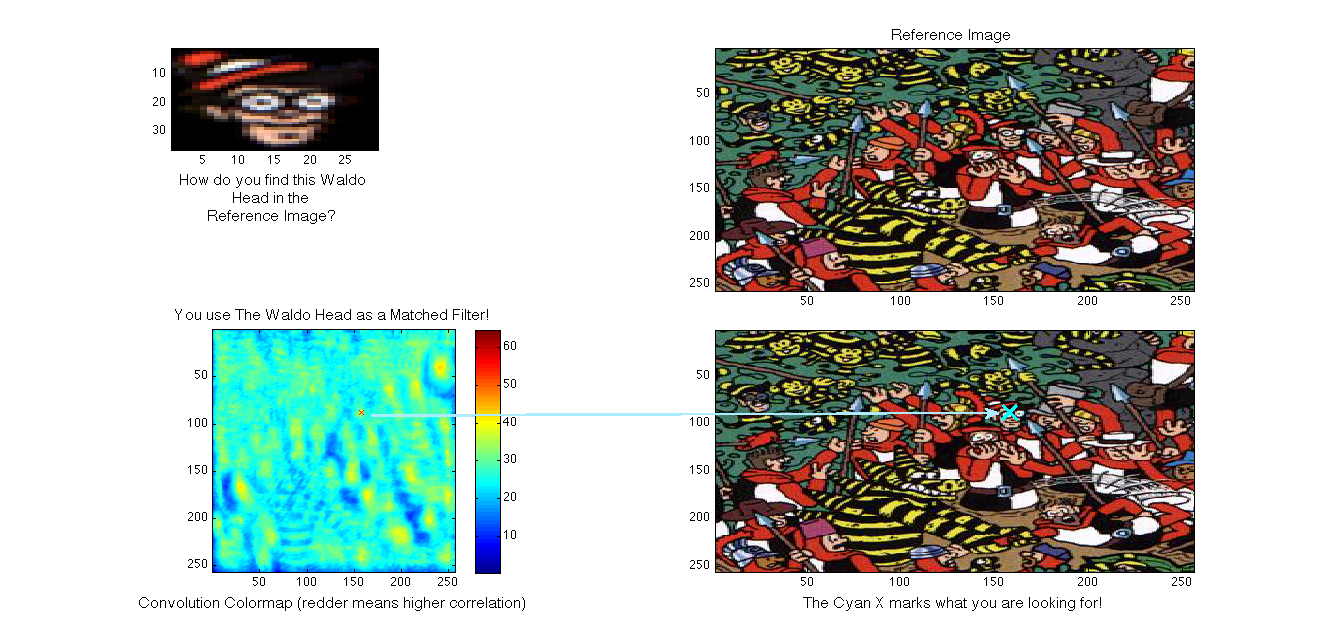 b)
b)entonces podríamos desarrollar fácilmente un programa para encontrar el parecido más cercano a la imagen de la cabeza de Waldo en la imagen más grande. Simplemente implementaríamos nuestro mismo algoritmo de filtro de coincidencia: tomar los productos internos en cada turno y ver qué tan grandes son nuestras respuestas resultantes. Esta idea se implementó en esta misma imagen para un Proyecto de Señales y Sistemas en la Universidad Rice (haga clic en el enlace para saber más).
Ejercicio\(\PageIndex{1}\): Pros and Cons
¿Cuáles son las ventajas del algoritmo de filtro emparejado para la detección de imágenes? ¿Cuáles son los inconvenientes de este método?
- Contestar
-
Este algoritmo es muy sencillo y por lo tanto fácil de codificar. No obstante, es susceptible a ciertos tipos de ruido -por ejemplo, sería difícil encontrar a Waldo si su cara estuviera girada, volteada, mayor o menor de lo esperado, o distorsionada de alguna otra manera.
Sistemas de Comunicaciones
Los detectores de filtro emparejados también se usan comúnmente en sistemas de comunicaciones. De hecho, son los detectores óptimos en el ruido gaussiano. Las señales en el mundo real suelen ser distorsionadas por el entorno que las rodea, por lo que existe una lucha constante para desarrollar formas de poder recibir una señal distorsionada y luego poder filtrarla de alguna manera para determinar cuál era la señal original. Los filtros coincidentes proporcionan una manera de comparar una señal recibida con dos posibles señales originales (“plantilla”) y determinar cuál es la coincidencia más cercana a la señal recibida.
Por ejemplo, a continuación tenemos un ejemplo simplificado de Frequency Shift Keying (FSK) donde tenemos la siguiente codificación para '1' y '0':
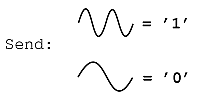
Con base en la codificación anterior, podemos crear señales digitales basadas en 0 y 1, juntando los dos “códigos” anteriores en un número infinito de formas. Para este ejemplo transmitiremos un número básico de 3 bits, 101, que se muestra en la Figura\(\PageIndex{8}\):
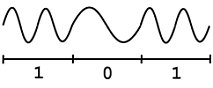
Ahora bien, la imagen de la señal anterior representa nuestra señal original que se transmitirá a través de algún sistema de comunicación, que inevitablemente pasará por el “canal de comunicaciones”, la parte del sistema que distorsionará y alterará nuestra señal. Mientras el ruido no sea demasiado grande, nuestro filtro emparejado debería evitar que tengamos que preocuparnos por estos cambios en nuestra señal transmitida. Una vez recibida esta señal, pasaremos la señal ruidosa a través de un sistema sencillo, similar a la versión simplificada que se muestra en la Figura\(\PageIndex{9}\):
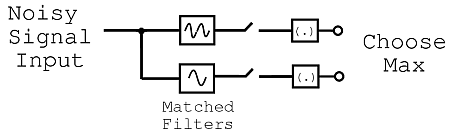
La figura\(\PageIndex{9}\) básicamente muestra que nuestra señal ruidosa se pasará (asumiremos que pasa en un “bit” a la vez) y esta señal se dividirá y pasará a dos detectores de filtro coincidentes diferentes. Cada uno comparará la señal ruidosa recibida con uno de los dos códigos que definimos para '1' y '0'. Entonces este valor se transmitirá y el valor que sea mayor (es decir, cualquiera que sea la señal de código FSK a la que más se parezca la señal ruidosa) será el valor que tome el receptor. Por ejemplo, el primer bit que se enviará a través será un '1' por lo que el nivel superior del diagrama de bloques tendrá un valor mayor, denotando así que un '1' fue enviado por la señal, aunque la señal pueda parecer muy ruidosa y distorsionada.
El siguiente ejemplo interactivo supone que nuestro transmisor envía 1000 bits, trazando cuántos de esos bits se reciben e interpretan correctamente como 1s y 0s, y además mantiene un recuento de cuántos son malinterpretados accidentalmente. Se puede jugar con la distancia entre la energía del “1" y el “0" (discriminabilidad), el grado de ruido presente en el canal, y la ubicación del criterio (umbral) para tener una idea de los fundamentos de la teoría de detección de señales.
Ejemplo\(\PageIndex{3}\)
Usemos un filtro coincidente para encontrar los bits “0" en una señal simple.
Vamos a usar la señal\(s_1(t)\) de Ejemplo\(\PageIndex{1}\) para representar los bits. \(s_1(t)\)representa 0, mientras que\(-s_1(t)\) representa 1.
\(0 \Rightarrow(b=1) \Rightarrow\left(s_{1}(t)=s(t)\right)\)para\(0≤t≤T\)
\(1 \Rightarrow(b=-1) \Rightarrow\left(s_{2}(t)=-s(t)\right)\)para\(0≤t≤T\)
\[X_{t}=\sum_{i=-P}^{P} b_{i} s(t-i T) \nonumber \]
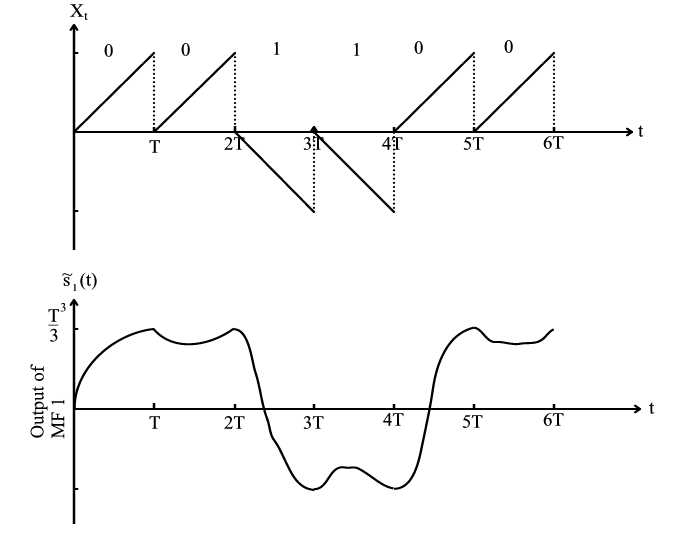
Figura\(\PageIndex{10}\)
La salida del filtro coincidente muestra claramente la ubicación de los bits “0".
Radar
Una de las primeras y más intrigantes formas de comunicación que utilizaron el concepto de filtro emparejado fue el radar. Una señal electromagnética conocida es enviada por un transmisor a un objetivo y reflejada fuera del objetivo de vuelta al emisor con un retardo de tiempo proporcional a la distancia entre el objetivo y el emisor. Esta señal escalada y desplazada en el tiempo se convoluciona entonces con la señal de plantilla original, y se anota el tiempo en el que la salida de esta convolución es más alta.
Esta tecnología resultó vital en la década de 1940 para los poderes que la poseían. Un breve conjunto de videos a continuación muestra los conceptos básicos de cómo funciona la tecnología, sus aplicaciones y su impacto en la Segunda Guerra Mundial.
Figura\(\PageIndex{11}\)
Vea el video en la Figura\(\PageIndex{12}\) para un análisis del mismo principio básico que se está aplicando a los sistemas de control de crucero adaptativo para el automóvil moderno.
Demostración de filtro emparejado
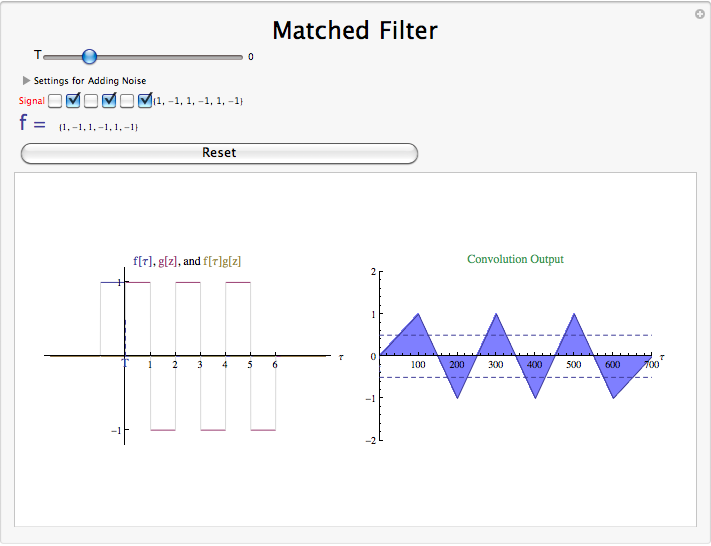
Resumen de filtros coincidentes
Como se puede ver, el detector de filtro emparejado es una importante aplicación de procesamiento de señales, rica tanto en conceptos teóricos como en aplicaciones prácticas. El filtro emparejado admite una amplia gama de usos relacionados con el reconocimiento de patrones, incluida la detección de imágenes, la demodulación por desplazamiento de frecuencia y la interpretación de señales de radar. A pesar de esta diversidad de propósitos, todas las aplicaciones de filtro coincidentes operan esencialmente de la misma manera. Cada miembro de algún conjunto de señales se compara con una señal objetivo evaluando el valor absoluto del producto interno de las dos señales después de la normalización. Sin embargo, los conjuntos de señales y las interpretaciones de resultados son específicos de la aplicación.


