14.1: Álgebra Lineal Básica
- Page ID
- 86602
Este breve tutorial sobre algunos términos clave en álgebra lineal no pretende reemplazar o ser muy útil para aquellos de ustedes que intentan obtener una visión profunda del álgebra lineal. Más bien, esta breve introducción a algunos de los términos e ideas del álgebra lineal pretende proporcionar un poco de antecedentes a aquellos que intentan comprender mejor o aprender sobre los vectores propios y las funciones propias, que juegan un papel importante en la obtención de algunas ideas importantes sobre Señales y Sistemas. El objetivo de estos conceptos será proporcionar un fondo para la descomposición de la señal y conducir a la derivación de la Serie de Fourier.
Independencia Lineal
Un conjunto de vectores\(\left\{x_{1}, x_{2}, \ldots, x_{k}\right\}\) en\(x_{i} \in \mathbb{C}^{n}\) son linealmente independientes si ninguno de ellos puede escribirse como una combinación lineal de los otros.
Definición: Linealmente Independiente
Para un conjunto dado de vectores\(\left\{x_{1}, x_{2}, \ldots, x_{n}\right\}\),, son linealmente independientes si
\[c_{1} x_{1}+c_{2} x_{2}+\dots+c_{n} x_{n}=0 \nonumber \]
sólo cuando\(c_{1}=c_{2}=\cdots=c_{n}=0\)
Ejemplo\(\PageIndex{1}\)
Se nos dan los siguientes dos vectores:
\ [\ begin {array} {c}
x_ {1} =\ left (\ begin {array} {c}
3\\
2
\ end {array}\ right)\\
x_ {2} =\ left (\ begin {array} {c}
-6\
-4\ end {array}
\ right)\ end {array}
\ end {array}\ nonumber\]
Éstas no son linealmente independientes como lo demuestra la siguiente afirmación, la cual, por inspección, puede verse que no se adhiere a la definición de independencia lineal señalada anteriormente.
\[\left(x_{2}=-2 x_{1}\right) \Rightarrow\left(2 x_{1}+x_{2}=0\right) \nonumber \]
Otro enfoque para revelar la independencia de los vectores es graficando los vectores. Al observar estos dos vectores geométricamente (como en la Figura\(\PageIndex{1}\)), se puede probar nuevamente que estos vectores no son linealmente independientes.
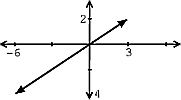
Ejemplo\(\PageIndex{2}\)
Se nos dan los siguientes dos vectores:
\ [\ begin {array} {l}
x_ {1} =\ left (\ begin {array} {l}
3\\
2
\ end {array}\ derecha)\\
x_ {2} =\ left (\ begin {array} {l}
1\\
2\ end {array}
\ right)\ end {array}
\ end {array}\ nonumber\]
Estos son linealmente independientes ya que
\[c_{1} x_{1}=-\left(c_{2} x_{2}\right) \nonumber \]
sólo si\(c_1=c_2=0\). Con base en la definición, esta prueba muestra que estos vectores son, en efecto, linealmente independientes. Nuevamente, también podríamos graficar estos dos vectores (ver Figura\(\PageIndex{2}\)) para verificar la independencia lineal.
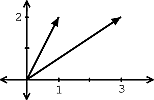
Ejercicio\(\PageIndex{1}\)
¿Son\(\left\{x_{1}, x_{2}, x_{3}\right\}\) linealmente independientes?
\ [\ begin {array} {l}
x_ {1} =\ left (\ begin {array} {l}
3\\
2
\ end {array}\ derecha)\\
x_ {2} =\ left (\ begin {array} {l}
1\\
2
\ end {array}\ derecha)\\
x_ {3} =\ left (\ begin {array} {c}
-1\\
0
\ end {array}\ right)
\ end {array}\ nonumber\]
- Contestar
-
Jugando con los vectores y haciendo un poco de prueba y error, descubriremos la siguiente relación:
\[x_{1}-x_{2}+2 x_{3}=0 \nonumber \]
Así hemos encontrado una combinación lineal de estos tres vectores que es igual a cero sin establecer los coeficientes iguales a cero. Por lo tanto, ¡estos vectores no son linealmente independientes!
Como hemos visto en los dos ejemplos anteriores, muchas veces la independencia de los vectores se puede ver fácilmente a través de una gráfica. Sin embargo esto puede no ser tan fácil cuando se nos dan tres o más vectores. ¿Se puede decir fácilmente si estos vectores son independientes o no de la\(\PageIndex{3}\) Figura? Probablemente no, razón por la cual el método utilizado en la solución anterior se vuelve importante.
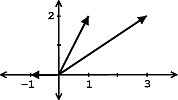
Nota
Un conjunto de\(m\) vectores en\(\mathbb{C}^{n}\) no puede ser linealmente independiente si\(m>n\).
Span
Definición: Word
El lapso de un conjunto de vectores\(\left\{x_{1}, x_{2}, \ldots, x_{k}\right\}\) es el conjunto de vectores que se pueden escribir como una combinación lineal de\(\left\{x_{1}, x_{2}, \ldots, x_{k}\right\}\)
\[\operatorname{span}\left(\left\{x_{1}, \ldots, x_{k}\right\}\right)=\left\{\alpha_{1} x_{1}+\alpha_{2} x_{2}+\cdots+\alpha_{k} x_{k}, \quad \alpha_{i} \in \mathbb{C}^{n}\right\} \nonumber \]
Ejemplo\(\PageIndex{3}\)
Dado el vector
\ [x_ {1} =\ izquierda (\ begin {array} {l}
3\\
2
\ end {array}\ derecha)\ nonumber\]
el lapso de\(x_1\) es una línea.
Ejemplo\(\PageIndex{4}\)
Dados los vectores
\ [\ begin {array} {l}
x_ {1} =\ left (\ begin {array} {l}
3\\
2
\ end {array}\ derecha)\\
x_ {2} =\ left (\ begin {array} {l}
1\\
2\ end {array}
\ right)\ end {array}
\ end {array}\ nonumber\]
el lapso de estos vectores es\(\mathbb{C}^{2}\).
Bases
Definición: Bases
Una base para\(\mathbb{C}^{n}\) es un conjunto de vectores que: (1) abarca\(\mathbb{C}^{n}\) y (2) es linealmente independiente.
Claramente, cualquier conjunto de vectores\(n\) linealmente independientes es una base para\(\mathbb{C}^n\).
Ejemplo\(\PageIndex{5}\)
Se nos da el siguiente vector
\ [e_ {i} =\ left (\ begin {array} {c}
0\\
\ vdots\\
0\\
1\\
0\
\ vdots\\
0
\ end {array}\ derecha)\ nonumber\]
donde el siempre\(1\) está en el lugar\(i\) th y los valores restantes son cero. Entonces la base para\(\mathbb{C}^n\) es
\[\left\{e_{i}, \quad i=[1,2, \ldots, n]\right\} \nonumber \]
Nota
\(\left\{e_{i}, \quad i=[1,2, \ldots, n]\right\}\)se llama la base estándar.
Ejemplo\(\PageIndex{6}\)
\ [\ begin {array} {c}
h_ {1} =\ left (\ begin {array} {c}
1\\
1
\ end {array}\ derecha)\\
h_ {2} =\ left (\ begin {array} {c}
1\\
-1\ end {array}
\ right)\ end {array}
\ end {array}\ nonumber\]
\(\left\{h_{1}, h_{2}\right\}\)es una base para\(\mathbb{C}^2\).
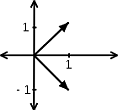
Si\(\left\{b_{1}, \ldots, b_{2}\right\}\) es una base para\(\mathbb{C}^n\), entonces podemos expresar cualquiera\(\boldsymbol{x} \in \mathbb{C}^{n}\) como una combinación lineal de los\(b_{i}\)'s:
\[x=\alpha_{1} b_{1}+\alpha_{2} b_{2}+\dots+\alpha_{n} b_{n}, \quad \alpha_{i} \in \mathbb{C} \nonumber \]
Ejemplo\(\PageIndex{7}\)
Dado el siguiente vector,
\ [x=\ left (\ begin {array} {l}
1\\
2
\ end {array}\ derecha)\ nonumber\]
escribir\(x\) en términos de nos\(\left\{e_{1}, e_{2}\right\}\) da
\[x=e_{1}+2 e_{2} \nonumber \]
Ejercicio\(\PageIndex{2}\)
Intenta escribir\(x\) en términos de\(\left\{h_{1}, h_{2}\right\}\) (definido en el ejemplo anterior).
- Contestar
-
\[x=\frac{3}{2} h_{1}+\frac{-1}{2} h_{2} \nonumber \]
En los dos ejemplos básicos anteriores,\(x\) es el mismo vector en ambos casos, pero podemos expresarlo de muchas maneras diferentes (damos solo dos de muchas, muchas posibilidades). Puedes llevar esto aún más lejos extendiendo esta idea de una base a los espacios funcionales.
Nota
Como se mencionó en la introducción, estos conceptos de álgebra lineal le ayudarán a prepararse para comprender la Serie de Fourier, lo que nos dice que podemos expresar funciones periódicas\(f(t)\),, en términos de sus funciones base,\(e^{j \omega_0 nt}\).


