14.2: vectores propios y valores propios

En esta sección, nuestros sistemas lineales serán n×n matrices de números complejos. Para un poco de trasfondo sobre algunos de los conceptos en los que se basa este módulo, refiérase a los fundamentos del álgebra lineal (Sección 14.1).

Autovectores y valores propios

Dejar\(A\) ser una\(n \times n\) matriz, donde\(A\) es un operador lineal sobre vectores en\(\mathbb{C}^n\).

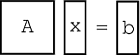
\[Ax=b \label{14.1} \]

donde\(x\) y\(b\) son\(n \times 1\) vectores (Figura\(\PageIndex{1}\)).

Figura\(\PageIndex{1}\): Ilustración de sistema lineal y vectores.

Definición: Eigenvector

Un vector propio de\(A\) es un vector\(\mathbf{v} \in \mathbb{C}^{n}\) tal que

\[A \mathbf{v}=\lambda \mathbf{v} \label{14.2} \]

donde\(\lambda\) se llama el valor propio correspondiente. \(A\)sólo cambia la longitud de\(\mathbf{v}\), no su dirección.

Modelo gráfico

A través de Figura\(\PageIndex{2}\) y Figura\(\PageIndex{3}\), veamos la diferencia entre la Ecuación\ ref {14.1} y la Ecuación\ ref {14.2}.

Figura\(\PageIndex{2}\): Representa la ecuación\ ref {14.1},\(A \mathbf{x}=\mathbf{b}\).

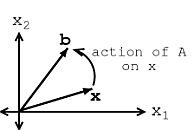
Si\(\mathbf{v}\) es un vector propio de\(A\), entonces solo cambia su longitud. Vea Figura\(\PageIndex{3}\) y observe cómo la longitud de nuestro vector es simplemente escalada por nuestra variable\(\lambda\),, llamada el valor propio:

Figura\(\PageIndex{3}\): Representa la ecuación\ ref {14.2},\(A \mathbf{v}=\lambda \mathbf{v}\).

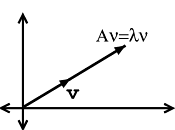
Nota

Cuando se trata de una matriz\(A\), los vectores propios son los vectores más simples posibles para operar.

Ejemplos

Ejercicio\(\PageIndex{1}\)

A partir de la inspección y comprensión de vectores propios, encontrar los dos vectores propios,\(v_1\) y\(v_2\), de

\ [A=\ left (\ begin {array} {cc}
3 & 0\\
0 & -1
\ end {array}\ derecha)\ nonumber\]

Además, ¿cuáles son los valores propios correspondientes,\(\lambda_1\) y\(\lambda_2\)? No te preocupes si estás teniendo problemas al ver estos valores a partir de la información dada hasta ahora, veremos formas más rigurosas de encontrar estos valores pronto.

Contestar

Los vectores propios que encontraste deberían ser:

\ [\ begin {array} {l}
v_ {1} =\ left (\ begin {array} {l}
1\\
0\ end {array}
\ derecha)\\
v_ {2} =\ left (\ begin {array} {l}
0\\
1\ end {array}\ right)
\ end {array}\ end {array}
\ end {array} \ nonumber\]

Y los valores propios correspondientes son

\[\lambda_1 = 3 \nonumber \]

\[\lambda_2 = -1 \nonumber \]

Ejercicio\(\PageIndex{2}\)

Demostrar que estos dos vectores,

\ [\ begin {array} {l}
v_ {1} =\ left (\ begin {array} {l}
1\\
1
\ end {array}\ derecha)\\
v_ {2} =\ left (\ begin {array} {c}
1\\
-1\ end {array}
\ right)\ end {array}
\ end {array}\ nonumber\]

son vectores propios de\(A\), donde\ (A=\ left (\ begin {array} {cc}
3 & -1\\
-1 & 3
\ end {array}\ right)\). Además, encuentra los valores propios correspondientes.

Contestar

Para probar que estos dos vectores son vectores propios, mostraremos que estos enunciados cumplen con los requisitos establecidos en la definición.

\ [\ begin {array} {c}
A v_ {1} =\ left (\ begin {array} {cc}
3 & -1\\
-1 & 3
\ end {array}\ right)\ left (\ begin {array} {c}

1\
\ end {array}\ right) =\ left (\ begin {array} {c}
2\\
2
\ end {array}\ derecha)\\
A v_ {2} =\ left (\ begin {array} {cc}
3 & -1\\
-1 & 3
\ end {array}\ derecha)\ left (\ begin {array} {c}
1\\
-1
\ end {array}\ right) =\ left (\ begin {array} {c}
4\\
-4\ end {array}
\ right)\ end {array}
\ end {array}\ nonumber\]

Estos resultados nos muestran que\(A\) solo escala los dos vectores (es decir, cambia su longitud) y así demuestra que la Ecuación\ ref {14.2} es cierta para los siguientes dos valores propios que se le pidió que encontrara:

\[\lambda_1 = 2 \nonumber \]

\[\lambda_2 = 4 \nonumber \]

Si necesitas más convincente, entonces uno también podría graficar fácilmente los vectores y su producto correspondiente con\(A\) para ver que los resultados son simplemente versiones escaladas de nuestros vectores originales,\(v_1\) y\(v_2\).

Conferencia Khan sobre vectores propios

Figura\(\PageIndex{4}\): video de Khan Academy - Intro duction t o Eigenvectors y Eigenvalues - 7:43 min.

Cálculo de valores propios y vectores propios

En los ejemplos anteriores, confiamos en su comprensión de la definición y en algunas observaciones básicas para encontrar y probar los valores de los vectores propios y los valores propios. No obstante, como probablemente puedas decir, encontrar estos valores no siempre será tan fácil. A continuación, recorremos un enfoque riguroso y matemático para calcular los valores propios y vectores propios de una matriz.

Encontrar valores propios

Encuentra\(\lambda \in \mathbb{C}\) tal que\(\mathbf{v} \neq \mathbf{0}\), donde\(\mathbf{0}\) está el “vector cero”. Comenzaremos con la Ecuación\ ref {14.2}, y luego trabajaremos nuestro camino hacia abajo hasta que encontremos una manera de calcular explícitamente\(\lambda\).

\ [\ begin {array} {c}
A\ mathbf {v} =\ lambda\ mathbf {v}\\
A\ mathbf {v} -\ lambda\ mathbf {v} =0\\
(A-\ lambda I)\ mathbf {v} =0
\ end {array}\ nonumber\]

En el paso anterior, utilizamos el hecho de que

\[\lambda \mathbf{v}=\lambda I \mathbf{v} \nonumber \]

donde\(I\) está la matriz de identidad.

\ [I=\ left (\ begin {array} {cccc}
1 & 0 &\ dots & 0\\
0 & 1 &\ dots & 0\\ 0 &\
0 &\ ddots &\ vdots\\
0 &\ dots &\ dots &\ dots & 1
\ end {array}\ derecha)\ nonumber\]

Entonces,\(A−\lambda I\) es sólo una nueva matriz.

Ejemplo\(\PageIndex{1}\)

Dada la siguiente matriz,\(A\), entonces podemos encontrar nuestra nueva matriz,\(A−\lambda I\).

\ [\ begin {array} {c}
A=\ left (\ begin {array} {cc}
a_ {1,1} & a_ {1,2}\
a_ {2,1} & a_ {2,2}
\ end {array}\ derecha)\\
A-\ lambda I=\ left (\ begin {array} {cc}
a_ {1,1} -\ lambda y a_ {1,2}\
a_ {} & a_ {2,2} -\ lambda
\ end {array}\ derecha)
\ end {array}\ nonumber\]

Si\((A−\lambda I) \mathbf{v} = 0\) para algunos\(\mathbf{v} \neq 0\), entonces no\(A− \lambda I\) es invertible. Esto significa:

\[\operatorname{det}(A-\lambda I)=0 \nonumber \]

Este determinante (mostrado directamente arriba) resulta ser una expresión polinómica (de orden\(n\)). Mira los ejemplos a continuación para ver qué significa esto.

Ejemplo\(\PageIndex{2}\)

Comenzando con matrix\(A\) (que se muestra a continuación), encontraremos la expresión polinómica, donde nuestros valores propios serán la variable dependiente.

\ [A=\ left (\ begin {array} {cc}
3 & -1\\
-1 & 3
\ end {array}\ derecha)\ nonumber\]

\ [A-\ lambda I=\ izquierda (\ begin {array} {cc}
3-\ lambda & -1\\
-1 & 3-\ lambda
\ end {array}\ derecha)\ nonumber\]

\[\operatorname{det}(A-\lambda I)=(3-\lambda)^{2}-(-1)^{2}=\lambda^{2}-6 \lambda+8 \nonumber \]

\[\lambda=\{2,4\} \nonumber \]

Ejemplo\(\PageIndex{3}\)

Comenzando con matrix\(A\) (que se muestra a continuación), encontraremos la expresión polinómica, donde nuestros valores propios serán la variable dependiente.

\ [\ begin {array} {c}
A=\ left (\ begin {array} {cc}
a_ {1,1} & a_ {1,2}\
a_ {2,1} & a_ {2,2}
\ end {array}\ derecha)\\
A-\ lambda I=\ left (\ begin {array} {cc}
a_ {1,1} -\ lambda y a_ {1,2}\
a_ {} & a_ {2,2} -\ lambda
\ end {array}\ derecha)\\
\ nombreoperador {det} (A-\ lambda I) =\ lambda^ {2} -\ izquierda (a_ {1,1} +a_ {2,2}\ derecha)\ lambda-a_ {2,1} a_ {1,2} +a_ {1,1} a_ {2,2}
\ end {array}\ nonumber\]

Si aún no lo has notado, calcular los valores propios equivale a calcular las raíces de

\[\operatorname{det}(A-\lambda I)=c_{n} \lambda^{n}+c_{n-1} \lambda^{n-1}+\dots+c_{1} \lambda+c_{0}=0 \nonumber \]

Conclusión

Por lo tanto, simplemente usando cálculo para resolver las raíces de nuestro polinomio podemos encontrar fácilmente los valores propios de nuestra matriz.

Encontrar vectores propios

Dado un valor propio,\(\lambda_i\), los vectores propios asociados están dados por

\ [\ begin {array} {c}
A\ mathbf {v} =\ lambda_ {i}\ mathbf {v}\\
A\ left (\ begin {array} {c}
v_ {1}\
\ vdots\\
v_ {n}
\ end {array}\ right) =\ left (\ begin {array} {c}
\ lambda_ {1} v_ {1}\\
\ vdots\\
\ lambda_ {n} v_ {n}
\ end {array}\ right)
\ end {array}\ nonumber\]

conjunto de\(n\) ecuaciones con\(n\) incógnitas. Simplemente resuelve las\(n\) ecuaciones para encontrar los vectores propios.

Conferencia Khan sobre Derivación de vectores propios y valores propios

Figura\(\PageIndex{5}\): video de Khan Academy - Exampl e Derivando vectores propios y valores propios - 5:39 min.

Punto Principal

Digamos que los vectores propios de\(A\)\(\left\{v_{1}, v_{2}, \ldots, v_{n}\right\}\),, span\(\mathbb{C}^n\), significado\(\left\{v_{1}, v_{2}, \ldots, v_{n}\right\}\) son linealmente independientes (Sección 14.1) y podemos escribir cualquiera\(\mathbf{x} \in \mathbb{C}^{n}\) como

\[\mathbf{x}=\alpha_{1} v_{1}+\alpha_{2} v_{2}+\cdots+\alpha_{n} v_{n} \label{14.3} \]

donde\(\left\{\alpha_{1}, \alpha_{2}, \ldots, \alpha_{n}\right\} \in \mathrm{C}\). Todo lo que estamos haciendo es reescribir\(\mathbf{x}\) en términos de vectores propios de\(A\). Entonces,

\ [\ begin {array} {c}
A\ mathbf {x} =A\ left (\ alpha_ {1} v_ {1} +\ alpha_ {2} v_ {2} +\ cdots+\ alpha_ {n} v_ {n}\ right)\
A\ mathbf {x} =\ alpha_ {1} A v_ {1} +\ alpha_ {2} A v_ {2} +\ cdots+\ alpha_ {n} A v_ {n}\\
A\ mathbf {x} =\ alpha_ {1}\ lambda_ {1} v_ {1} +\ alpha_ {2}\ lambda_ {2} v_ {2} +\ cdots+\ alfa_ {n}\ lambda_ {n} v_ {n} =b
\ final {array}\ nonumber\]

Por lo tanto podemos escribir,

\[\mathbf{x}=\sum_{i} \alpha_{i} v_{i} \nonumber \]

y esto nos lleva al siguiente sistema representado:

Figura\(\PageIndex{6}\): Representación del sistema donde rompemos nuestro vector\(\mathbf{x}\),, en una suma de sus vectores propios.

donde en Figura\(\PageIndex{6}\) tenemos,

\[b=\sum_{i} \alpha_{i} \lambda_{i} v_{i} \nonumber \]

Punto principal:

Al dividir un vector,\(\mathbf{x}\), en una combinación de vectores propios, el cálculo de\(A\mathbf{x}\) se rompe en piezas “fáciles de tragar”.

Problema de práctica

Ejercicio\(\PageIndex{3}\)

Para la siguiente matriz,\(A\) y vector,\(\mathbf{x}\), resolver para su producto. Intenta resolverlo usando dos métodos diferentes: directamente y usando vectores propios.

\ [\ begin {aligned}
A &=\ left (\ begin {array} {cc}
3 & -1\\
-1 & 3\ end {array}
\ right)\\
&\ mathbf {x} =\ left (\ begin {array} {l}
5\\
3\ end {array}\ right)
\ end {array}\ right)
\ end {alineado}\ nonumber\]

Contestar

Método directo (use multiplicación matricial básica)

\ [A\ mathbf {x} =\ left (\ begin {array} {cc}
3 & -1\\
-1 & 3
\ end {array}\ derecha)\ left (\ begin {array} {l}
5\\
3
\ end {array}\ right) =\ left (\ begin {array} {c}
12\\
4
\ end {array}\ derecha)\ nonumber\]

vectores propios (usa los vectores propios y los valores propios que encontramos anteriormente para esta misma matriz)

\ [\ begin {array} {c}
v_ {1} =\ left (\ begin {array} {c}
1\\
1
\ end {array}\ derecha)\\
v_ {2} =\ left (\ begin {array} {c}
1\\
-1
\ end {array}\ right)\
\ lambda _ {1} =2\\
\ lambda_ {2} =4
\ end {array}\ nonumber\]

Como se muestra en la Ecuación\ ref {14.3}, queremos representar\(x\) como una suma de sus vectores propios escalados. Para este caso, contamos con:

\ [\ begin {array} {c}
\ mathbf {x} = 4 v_ {1} +v_ {2}\\
\ mathbf {x} =\ left (\ begin {array} {c}
5\\
3
\ end {array}\ right) =4\ left (\ begin {array} {c}
1\\
1
\ end {array}\ derecha) +\ left (\ begin {array} {c}
1\\
-1
\ end {array}\ right)\\
A\ mathbf {x} = A\ left (4 v_ {1} +v_ {2}\ derecha) =\ lambda_ {i}\ left (4 v_ {1} +v_ {2}\ derecha)
\ end {array}\ nonumber\]

Por lo tanto, tenemos

\ [A\ mathbf {x} =4\ times 2\ left (\ begin {array} {l}
1\\
1
\ end {array}\ right) +4\ left (\ begin {array} {c}
1\\
-1
\ end {array}\ right) =\ left (\ begin {array} {c}
12\\
4
\ end {array}\ derecha)\ nonumber\]

Observe que este método usando vectores propios no requirió multiplicación matricial. Esto puede haber parecido más complicado aquí, pero imagínese\(A\) ser realmente grande, ¡o incluso solo unas pocas dimensiones más grandes!