15.4: Productos internos

Última actualización
Guardar como PDF

Page ID: 86584

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Definición: Producto interno

Es posible que hayas encontrado productos internos, también llamados productos punto,\(\mathbb{R}^n\) antes en algunos de tus cursos de matemáticas o ciencias. Si no, definimos el producto interno de la siguiente manera, dado que tenemos algunos\(\boldsymbol{x} \in \mathbb{R}^{n}\) y\(\boldsymbol{y} \in \mathbb{R}^{n}\).

Definición: Producto interno estándar

El producto interno estándar se define matemáticamente como:

\ [\ begin {alineado}
\ langle\ negridsymbol {x},\ negridsymbol {y}\ rangle &=\ negritas {y} ^ {T}\ símbolo en negrita {x}\\
&=\ izquierda (\ begin {array} {cccc}
y_ {0} & y_ {1} &\ dots & y_ {n-1}
\ end {array}\ derecha)\ left (\ begin {array} {c}
x_ {0}\\
x_ {1}\\
\ vdots\\
x_ {n-1}
\ end {array}\ derecha)\\
&=\ suma_ {i=0} ^ {n-1} x_ {i} y_ {i}
\ end {alineado}\ nonumber\]

Producto interno en 2-D

Si tenemos\(\boldsymbol{x} \in \mathbb{R}^2\) y\(\boldsymbol{y} \in \mathbb{R}^2\), entonces podemos escribir el producto interno como

\[\langle\boldsymbol{x}, \boldsymbol{y}\rangle=\|\boldsymbol{x}\|\|\boldsymbol{y}\| \cos (\theta) \nonumber \]

donde\(\theta\) esta el angulo entre\(\boldsymbol{x}\) y\(\boldsymbol{y}\).

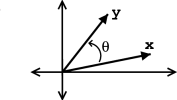
Figura\(\PageIndex{1}\): Gráfica general de vectores y ángulo referidos en las ecuaciones anteriores.

Geométricamente, el producto interno nos habla de la fuerza de\(\boldsymbol{x}\) en la dirección de\(\boldsymbol{y}\).

Ejemplo\(\PageIndex{1}\)

Por ejemplo, si\(\|x\|=1\), entonces

\[<x, y>=\|y\| \cos (\theta) \nonumber \]

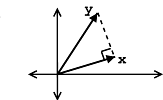
Figura\(\PageIndex{2}\): Gráfica de dos vectores del ejemplo anterior.

Las siguientes características son reveladas por el producto interno:

\(\langle \boldsymbol{x}, \boldsymbol{y}\rangle\)mide la longitud de la proyección de\(\boldsymbol{y}\) sobre\(\boldsymbol{x}\).
\(\langle \boldsymbol{x}, \boldsymbol{y}\rangle\)es máximo (para dado\(\|\boldsymbol{x}\|\),\(\|\boldsymbol{y}\|\)) cuando\(\boldsymbol{x}\) y\(\boldsymbol{y}\) están en la misma dirección (\((\theta=0) \Rightarrow(\cos (\theta)=1)\)).
\(\langle \boldsymbol{x}, \boldsymbol{y}\rangle\)es cero cuando\((\cos (\theta)=0) \Rightarrow\left(\theta=90^{\circ}\right)\), es decir,\(\boldsymbol{x}\) y\(\boldsymbol{y}\) son ortogonales.

Reglas internas del producto

En general, un producto interno en un espacio vectorial complejo es solo una función (tomar dos vectores y devolver un número complejo) que satisface ciertas reglas:

Simetría conjugada:\[\langle \boldsymbol{x}, \boldsymbol{y}\rangle=\overline{\langle \boldsymbol{x}, \boldsymbol{y}\rangle} \nonumber \]
Escalado:\[\langle\alpha \boldsymbol{x}, \boldsymbol{y} \rangle=\alpha\langle(\boldsymbol{x}, \boldsymbol{y})\rangle \nonumber \]
Aditividad:\[\langle \boldsymbol{x}+\boldsymbol{y}, \boldsymbol{z} \rangle=\langle \boldsymbol{x}, \boldsymbol{z}\rangle+\langle \boldsymbol{y}, \boldsymbol{z}\rangle \nonumber \]
“Positividad”:\[\langle \boldsymbol{x}, \boldsymbol{x} \rangle >0, \boldsymbol{x} \neq 0 \nonumber \]

Definición: Ortogonal

Nosotros decimos eso\(\boldsymbol{x}\) y\(\boldsymbol{y}\) son ortogonales si:

\[\langle\boldsymbol{x}, \boldsymbol{y}\rangle=0 \nonumber \]