15.14: Aproximación y Proyecciones en el Espacio Hilbert

Introducción

Dada una línea 'l' y un punto 'p' en el plano, ¿cuál es el punto más cercano 'm' a 'p' en 'l'?

Figura\(\PageIndex{1}\): Figura del punto 'p' y la línea 'l' mencionados anteriormente.

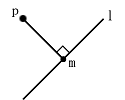
Mismo problema: Dejar\(x\) y\(v\) ser vectores en\(\mathbb{R}^2\). Diga\(\|v\|=1\). ¿Para qué valor de\(\alpha\) se\(\|x-\alpha v\|_{2}\) minimiza? (¿qué punto en span {v} se aproxima mejor\(x\)?)

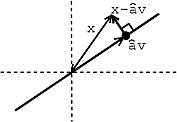
Figura\(\PageIndex{2}\)

La condición es esa\(x-\widehat{\alpha} v\) y\(\alpha v\) son ortogonales.

Cálculo α

¿Cómo calcular\(\widehat{a}\)?

Sabemos que (\(x-\widehat{\alpha} v\)) es perpendicular a cada vector en span {v}, entonces

\ [\ begin {array} {l}
\ langle x-\ sombrero ancho {\ alfa} v,\ beta v\ rangle=0,\ forall (\ beta)\
\ bar {\ beta}\ langle (x, v)\ rangle-\ sombrero ancho {\ alfa}\ bar {\ beta}\ langle (v, v)\ rangle=0
\ end {array}\ er\]

porque\(\langle v, v\rangle=1\), por lo

\[(\langle(x, v)\rangle-\hat{\alpha}=0) \Rightarrow(\hat{\alpha}=\langle x, v\rangle) \nonumber \]

Vector más cercano en span {v} =\(\langle(x, v)\rangle v\), donde\(\langle(x, v)\rangle v\) está la proyección de\(x\) sobre\(v\).

Podemos hacer lo mismo en dimensiones superiores.

Ejercicio\(\PageIndex{1}\)

\(V \subset H\)Sea un subespacio de un espacio Hilbert (Sección 15.4)\(H\). Dejemos\(x \in H\) que se den. Encuentra el\(y \in V\) que mejor se\(x\) aproxima. es decir,\(\|x-y\|\) se minimiza.

Contestar

1. Encuentre una base ortonormal\(\left\{b_{1}, \ldots, b_{k}\right\}\) para\(V\)
2. \(x\)Proyectar sobre el\(V\) uso\[y=\sum_{i=1}^{k}\left\langle\left(x, b_{i}\right)\right\rangle b_{i} \nonumber \] entonces\(y\) es el punto más cercano en\(V\) x y\((x-y) \perp V(\langle x-y, v\rangle=0, \quad \forall(v) \in V\)

Ejemplo\(\PageIndex{1}\)

\(x \in \mathbb{R}^{3}\),\ (V=\ operatorname {span}\ left (\ left\ {\ left (\ begin {array} {l}
1\\
0\
0
\ end {array}\ right),\ left (\ begin {array} {l}
0\\
1\
0
\ end {array}\ right)\ right\}\ right)\),\ (x=\ left (\ begin { array} {l}
a\\
b\\
c
\ end {array}\ right)\). Entonces,

\ [y=\ suma_ {i=1} ^ {2}\ izquierda\ langle\ izquierda (x, b_ {i}\ derecha)\ derecha\ rangle b_ {i} =a\ izquierda (\ begin {array} {l}
1\\

0
\ 0\ end {array}\ derecha) +b\ left (\ begin {array} {l}
0\\
1\
0
\ final array}\ derecha) =\ izquierda (\ begin { array} {l}
a\\
b\\
0
\ end {array}\ derecha)\ nonumber\]

Ejemplo\(\PageIndex{2}\)

V = {espacio de señales periódicas con frecuencia no mayor que\(3w_0\)}. Dado f (t) periódico, ¿cuál es la señal en V que mejor se aproxima a f?

1. \(\left\{\frac{1}{\sqrt{T}} e^{j w_{0} k t}, k=-3,-2, \dots, 2,3\right\}\)es una ONB para V
2. \(g(t)=\frac{1}{T} \sum_{k=-3}^{3}\left\langle\left(f(t), e^{j w_{0} k t}\right)\right\rangle e^{j w_{0} k t}\)es la señal más cercana en V a f (t) ⇒ reconstruir f (t) usando solo 7 términos de su serie de Fourier.

Ejemplo\(\PageIndex{3}\)

Let V = {funciones por partes constante entre los enteros}

1. ONB para V.

\ [b_ {i} =\ left\ {\ begin {array} {l}
1\ text {if} i-1\ leq t<i\\
0\ text {de lo contrario}
\ end {array}\ right. \ nonumber\]

donde\(\left\{b_{i}\right\}\) es una ONB.

¿La mejor aproximación constante por partes?

\ [\ begin {array} {c}
g (t) =\ suma_ {i=-\ infty} ^ {\ infty}\ izquierda\ langle\ izquierda (f, b_ {i}\ derecha)\ derecha\ rangle b_ {i}\
\ izquierda\ langle f, b_ {i}\ derecha\ rangle=\ int_ {-\ infty} ^ {\ infty} f (t) b_ {i} (t)\ mathrm {d} t=\ int_ {i-1} ^ {i} f (t)\ mathrm {d} t
\ end {array}\ nonumber\]

Ejemplo\(\PageIndex{4}\)

Esta demostración explora la aproximación utilizando una base de Fourier y una base de Wavelet Haar. Consulta aquí las instrucciones sobre cómo usar la demo.