1.3: El Degradado y el Operador Del

Gradiente

A menudo nos preocupan las propiedades de un campo escalar f (x, y, z) alrededor de un punto en particular. La regla de diferenciación en cadena nos da entonces el cambio incremental df en f para un pequeño cambio en la posición de (x, y, z) a (x + dx, y + dy, z + dz):

\[df = \frac{\partial f}{\partial x} dx + \frac{\partial f}{\partial y} dy + \frac{\partial f}{\partial z} dz \nonumber \]

Si el vector de distancia diferencial general dl se define como

\[\textbf{dl} = dx \textbf{i}_{z} + dy \textbf{i}_{y} + dz \textbf{i}_{z} \nonumber \]

(1) se puede escribir como el producto punto:

\[df = (\frac{\partial f}{\partial x} \textbf{i}_{x} + \frac{\partial f}{\partial y} \textbf{i}_{y} + \frac{\partial f}{\partial z} \textbf{i}_{z}) \cdot \textbf{dl} \\ = \textrm{grad} \: f \cdot \textbf{dl} \nonumber \]

donde los términos derivados espaciales entre paréntesis se definen como el gradiente de f:

\[\textrm{grad } f = \nabla f = \frac{\partial f}{\partial x} \textbf{i}_{x} + \frac{\partial f}{\partial y} \textbf{i}_{y} + \frac{\partial f}{\partial z} \textbf{i}_{z} \nonumber \]

El símbolo\(\nabla\) con el término gradiente se introduce como un operador vectorial general, denominado operador del:

\[\nabla = \textbf{i}_{x} \frac{\partial}{\partial x} + \textbf{i}_{y} \frac{\partial}{\partial y} + \textbf{i}_{z} \frac{\partial}{\partial z} \nonumber \]

Por sí mismo el operador del no tiene sentido, pero cuando premultiplica una función escalar, se define la operación de gradiente. Pronto veremos que el punto y los productos cruzados entre el operador del y un vector también definen operaciones útiles.

Con estas definiciones, el cambio en f de (3) puede escribirse como

\[df = \nabla f \cdot \textbf{dl} = \vert \nabla f \vert \: dl \: \cos \: \theta \nonumber \]

donde\(\theta\) es el ángulo entre\(\nabla f\) Vf y el vector de posición dl. La dirección que maximiza el cambio en la función f es cuando dl es colineal con\(\nabla f(\theta = 0)\). El gradiente tiene así la dirección de cambio máximo en f. Movimientos en la dirección a lo largo de líneas de constante f tienen\(\theta = \pi/2\) y así por definición df =0.

Coordenadas curvilíneas

cilíndrico

El gradiente de una función escalar se define para cualquier sistema de coordenadas como esa función vectorial que cuando está punteada con dl da df. En coordenadas cilíndricas el cambio diferencial en f (r,\(\phi\), z) es

\[df = \frac{\partial f}{\partial \textrm{r}} d \textrm{r} + \frac{\partial f}{\partial \phi} d \phi + \frac{\partial f}{\partial z} dz \nonumber \]

El vector de distancia diferencial es

\[\textbf{dl} = d \textrm{r} \textbf{i}_{\textrm{r}} + \textrm{r} d \phi \: \textbf{i}_{\phi} + dz \: \textbf{i}_{z} \nonumber \]

para que el gradiente en coordenadas cilíndricas sea

\[df = \nabla f \cdot \textbf{dl} \Rightarrow \nabla f = \frac{\partial f}{\partial r} \textbf{i}_{\textrm{r}} + \frac{1}{\textrm{r}} \frac{\partial f}{\partial \phi} \textrm{i}_{\phi} + \frac{\partial f}{\partial z} \textbf{i}_{\textrm{z}} \nonumber \]

Esférico

De manera similar en coordenadas esféricas el vector de distancia es

\[\textbf{dl} = dr \textbf{i}_{r} + r \: d \theta \: \textbf{i}_{\theta} + r \: \sin \: \theta \: d \phi \: \textbf{i}_{\phi} \nonumber \]

con el cambio diferencial de f (r,\(\theta\),\(\phi\)) como

\[df = \frac{\partial f}{\partial r} dr + \frac{\partial f}{\partial \theta} d \theta + \frac{\partial f}{\partial \phi} d \phi = \nabla f \cdot \textbf{dl} \nonumber \]

El uso de (10) en (11) da el gradiente en coordenadas esféricas como

\[\nabla f = \frac{\partial f}{\partial r} \textbf{i}_{r} + \frac{1}{r} \frac{\partial f}{\partial \theta} \textbf{i}_{\theta} + \frac{1}{r \: \sin \theta} \frac{\partial f}{\partial \phi} \textbf{i}_{\phi} \nonumber \]

Ejemplo 1-4: Gradiente

Encuentra el gradiente de cada una de las siguientes funciones donde a y b son constantes:

1. \(f = ax^{2}y + by^{3}z\)
2. \(f = a \textrm{r}^{2} \: \sin \: \phi + b \textrm{r} z \: \cos \: 2 \phi\)
3. \(f = \frac{a}{r} = br \: \sin \: \theta \: \cos \: \phi\)

Solución

a)\(\nabla f = \frac{\partial f}{\partial x} \textbf{i}_{x} + \frac{\partial f}{\partial y} \textbf{i}_{y} + \frac{\partial f}{\partial z} \textbf{i}_{z} = 2axy \textbf{i}_{x} + (ax^{2} + 3 by^{2} z) \textbf{i}_{y} + by^{3} \textbf{i}_{z}\)

b)\(\nabla f = \frac{\partial f}{\partial \textbf{r}} \textbf{i}_{\textrm{r}} + \frac{1}{\textrm{r}} \frac{\partial f}{\partial \phi} \textbf{i}_{\phi} + \frac{\partial f}{\partial z} \textbf{i}_{z} = (2a \textrm{r} \: \sin \: \phi + bz \: \cos \: 2 \phi) \textbf{i}_{\textrm{r}} + (a \textrm{r} \: \cos \: \phi - 2bz \: \sin \: 2 \phi) \textbf{i}_{\phi} + b \textrm{r} \: \cos \: 2 \phi \textbf{i}_{z}\)

c)\(\nabla f = \frac{\partial f}{\partial r} \textbf{i}_{r} + \frac{1}{r} \frac{\partial f}{\partial \theta} \textbf{i}_{\theta} + \frac{1}{r \: \sin \: \theta} \frac{\partial f}{\partial \phi} \textbf{i}_{\phi} = (- \frac{a}{r^{2}} + b \: \sin \: \theta \: \cos \phi) \textbf{i}_{r} + b \: \cos \: \theta \: \cos \: \phi \textbf{i}_{\theta} - b \: \sin \: \phi \textbf{i}_{\phi}\)

Línea Integral

En la Sección 1-2-4 motivamos el uso del producto punto a través de la definición de trabajo incremental como dependiendo únicamente del componente de fuerza\(F\) en la dirección del desplazamiento diferencial de un objeto\(dl\). Si el objeto se mueve a lo largo de una trayectoria, el trabajo total se obtiene sumando los trabajos incrementales a lo largo de cada pequeño desplazamiento en la trayectoria como en la Figura 1-11. Si rompemos el camino en\(N\) pequeños desplazamientos

Figura 1-11 El trabajo total en mover un cuerpo sobre una trayectoria es aproximadamente igual a la suma de trabajos incrementales en mover el cuerpo cada pequeña distancia incremental dl. A medida que las distancias diferenciales se acercan a la longitud cero, la suma se convierte en una integral de línea y el resultado es exacto.

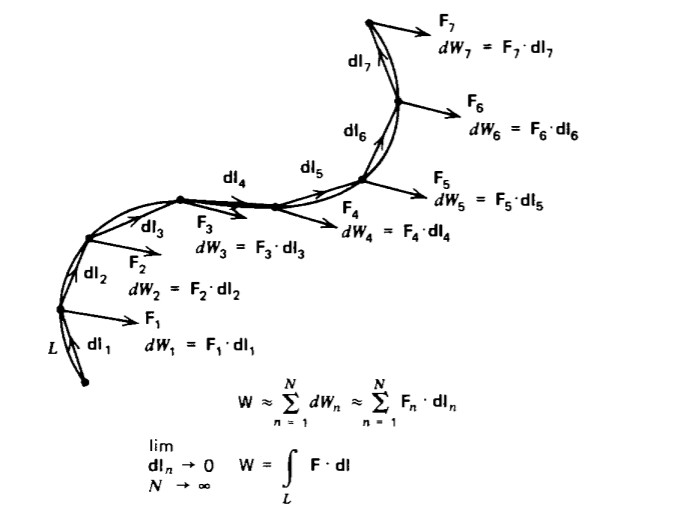
dl ₁, dl ₂,..., dl _N, el trabajo realizado es aproximadamente

\[W \approx \textbf{F}_{1} \cdot \textbf{dl}_{1} + \textbf{F}_{2} \cdot \textbf{dl}_{2} + \textbf{F}_{3} \cdot \textbf{dl}_{3} + ... + \textbf{F}_{N} \cdot \textbf{dl}_{N} \approx \sim_{n=1}^{N} \: \textbf{F}_{n} \cdot \textbf{dl}_{n} \nonumber \]

El resultado se vuelve exacto en el límite a medida que\(N\) se vuelve grande con cada desplazamiento\(dl\) llegando a ser infinitesimalmente pequeño:

\[W = \lim_{N\rightarrow \infty \\ \textbf{dl}_{\textbf{n}} \rightarrow 0} \sum^{N}_{n = 1} \textbf{F}_{n} \cdot \textbf{dl}_{n} = \int_{L} \textbf{F} \cdot \textbf{dl} \nonumber \]

En particular, integremos (3) sobre una trayectoria entre los dos puntos a y b en la Figura 1-12a:

\[\int_{a}^{b} df = f_{\vert_{b}} = f_{\vert_{a}} = \int_{a}^{b} \nabla f \cdot f \textbf{dl} \nonumber \]

Debido a que\(df\) es un diferencial exacto, su integral de línea depende únicamente de los puntos finales y no de la forma del contorno en sí. Así, todas las trayectorias entre a y b en la Figura 1-12a tienen la misma línea integral de\(\nabla f\), sin importar cuál sea la función f. Si el contorno es un trazado cerrado de manera que a = b, como en

Figura 1-12 El componente del gradiente de una función integrada a lo largo de un contorno de línea depende únicamente de los puntos finales y no del contorno en sí. (a) Cada uno de los contornos tiene los mismos puntos inicial y final en a y b para que todos tengan la misma línea integral de\(\nabla f\). b) Cuando todos los contornos estén cerrados con el mismo punto inicial y final en a, la integral de línea de\(\nabla f\) es cero. (c) La integral de línea del gradiente de la función en el Ejemplo (1-5) desde el origen hasta el punto P es la misma para todos los caminos.

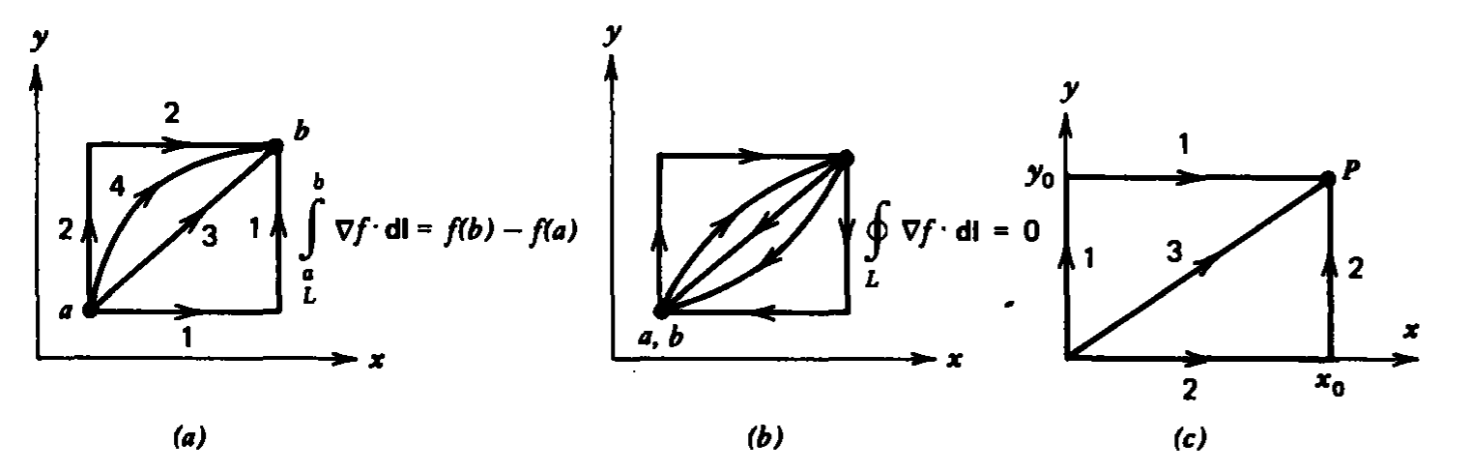
Figura 1-12b, entonces (15) es cero:

\[\oint_{L} \nabla f \cdot \textbf{dl} = f_{\vert_{a}} - f_{\vert_{a}} = 0 \nonumber \]

donde indicamos que el camino está cerrado por el círculo pequeño en el signo integral f. La integral de línea del gradiente de una función alrededor de una ruta cerrada es cero.

Ejemplo 1-5: Línea Integral

Para\(f = x^{2}y\), verificar (15) para los caminos mostrados en la Figura 1-12 c entre el origen y el punto P en (x ₀, y ₀).

Solución

El cambio total en f entre 0 y P es

\(\int_{0}^{P} df = f_{\vert_{P}} -f_{\vert_{0}} = x^{2}_{0}y_{0}\)

De la línea integral a lo largo del camino me encontramos

\(\int_{0}^{P} \nabla f \cdot \textbf{dl} = \int_{y=0 \\ x=0}^{y_{0}} {\underbrace{\frac{\partial f}{\partial y}}_{x^{2}}} \nearrow^{0} \: dy \int_{x = 0 \\ y = y_{0}}^{x_{0}} \: \underbrace{\frac{\partial f}{\partial x}}_{2xy} dx = x_{0}^{2}y_{0}\)

De igual manera, a lo largo del camino 2 también obtenemos

\(\int_{0}^{P} \nabla f \cdot \textbf{dl} = \int_{x=0 \\ y=0}^{x_{0}} \underbrace{\frac{\partial f}{\partial x}}_{2xy} \nearrow^{0} \: dx + \int_{y=0 \\ x=x_{0}}^{y_{0}} \: \underbrace{\frac{\partial f}{\partial y}}_{x^{2}} dy = x_{0}^{2}y_{0}\)

mientras que a lo largo del camino 3 debemos relacionar x e y a lo largo de la línea recta como

\(y = \frac{y_{0}}{x_{0}}x \Rightarrow dy = \frac{y_{0}}{x_{0}} dx\)

para rendir

\(\int_{0}^{P} \nabla f \cdot \textbf{dl} = \int_{0}^{P} (\frac{\partial f}{\partial x} dx + \frac{\partial f}{\partial y} dy) = \int_{x=0}^{x_{0}} \frac{3 y_{0}x^{2}}{x_{0}} dx = x_{0}^{2}y_{0}\)