1.5: El teorema de Curl y Stokes

Curl

Hemos utilizado el ejemplo de trabajo varias veces anteriormente para motivar relaciones vectoriales e integrales particulares. Hagámoslo una vez más considerando la línea integral de un vector alrededor de un camino cerrado llamado circulación:

\[C = \oint_{L} \textbf{A} \cdot \textbf{dl} \nonumber \]

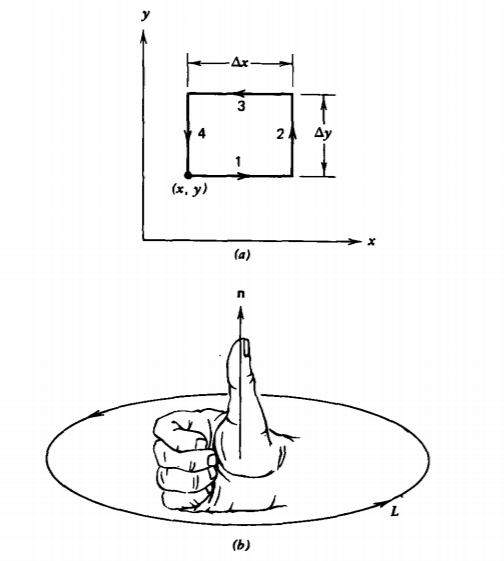
donde si\(C\) es la obra, A sería la fuerza. Evaluamos (1) para el contorno rectangular infinitesimal en la Figura 1-19a:

\[C = \int_{x \\ 1}^{x + \Delta x} A_{x}(y) dx + \int_{y\\2}^{y + \Delta y} A_{y}(x + \Delta x) dy + \int_{x + \Delta x \\ 3}^{x} A_{x}(y+ \Delta y) dx + \int_{y + \Delta y \\ 4}^{y} A_{y}(x)dy \nonumber \]

Los componentes de A son aproximadamente constantes sobre cada pata de contorno de tamaño diferencial de manera que (2) se aproxima como

\[C \approx \left(\dfrac{[A_{x}(y)-A_{x}(y + \Delta y)]}{\Delta y} + \dfrac{[A_{y}(x + \Delta x) - A_{y}(x)]}{\Delta x}\right) \Delta x \Delta y \nonumber \]

donde los términos se factorizan de manera que en el límite como\(\Delta x\) y\(\Delta y\) se vuelven infinitesimalmente pequeños, (3) se vuelve exacto y los términos entre corchetes definen derivadas parciales:

\[\lim_{\Delta x \rightarrow 0 \\ \Delta y \rightarrow 0 \\ \Delta S_{z} = \Delta x \Delta y} \: C = (\dfrac{\partial A_{y}}{\partial x} - \dfrac{\partial A_{x}}{\partial y}) \Delta S_{z} \nonumber \]

Figura 1-19 (a) Contorno rectangular infinitesimal utilizado para definir la circulación. b) La regla de la derecha determina la dirección positiva perpendicular a un contorno.

El contorno en la Figura 1-19 a podría haber sido tan fácilmente en los planos xz o yz donde (4) equivalentemente se convertiría

\[C = (\dfrac{\partial A_{z}}{\partial y} - \dfrac{\partial A_{y}}{\partial z}) \Delta S_{x} \: \: (yz \textrm{ plane}) \\ C = (\dfrac{\partial A_{x}}{\partial z} - \dfrac{\partial A_{z}}{\partial x}) \Delta S_{y} \: \: (xz \textrm{ plane}) \nonumber \]

por permutaciones positivas simples de x, y y z.

Las derivadas parciales en (4) y (5) son solo componentes del producto cruzado entre el vector del operador de la Sección 1-3-1 y el vector A. Esta operación se llama el rizo de A y también es un vector:

\[\textrm{curl} \textbf{ A} = \nabla \times \textbf{A} = \textrm{det} \begin{vmatrix} \textbf{i}_{x} & \textbf{i}_{y} & \textbf{i}_{z} \\ \dfrac{\partial}{\partial x} & \dfrac{\partial}{\partial y} & \dfrac{\partial}{\partial z} \\ A_{x} & A_{y} & A_{z} \end{vmatrix} \\ = \textbf{i}_{x}(\dfrac{\partial A_{z}}{\partial y} - \dfrac{\partial A_{y}}{\partial z}) + \textbf{i}_{y}(\dfrac{\partial A_{x}}{\partial z} - \dfrac{\partial A_{z}}{\partial x}) + \textbf{i}_{z}(\dfrac{\partial A_{y}}{\partial x} - \dfrac{\partial A_{x}}{\partial y}) \nonumber \]

La permutación cíclica de (x, y, z) permite recordar fácilmente (6) como se describe en la Sección 1-2-5.

En términos de la operación de rizo, la circulación para cualquier contorno de tamaño diferencial se puede escribir de forma compacta como

\[C = (\nabla \times \textbf{A}) \cdot \textbf{dS} \nonumber \]

donde dS = n dS es el elemento de área en la dirección del vector normal n perpendicular al plano del contorno en el sentido dado por la regla de la derecha al atravesar el contorno, ilustrado en la Figura 1-19 b. Enroscar los dedos de la mano derecha en la dirección de recorrido alrededor del contorno coloca el pulgar en la dirección de la n normal.

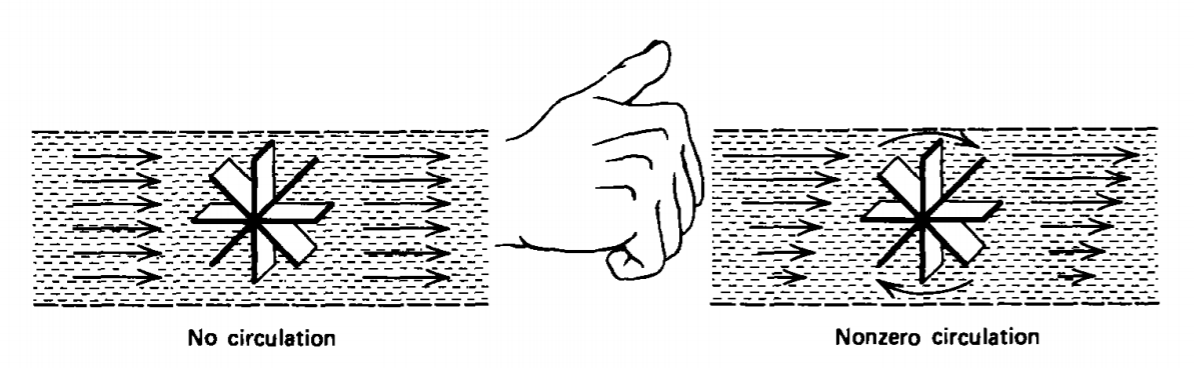
Para una interpretación física del rizo es conveniente seguir utilizando un campo de velocidad de fluido como modelo aunque los resultados generales y teoremas son válidos para cualquier campo vectorial. Si se imagina que una pequeña rueda de paletas se coloca sin perturbaciones en un flujo de fluido, se dice que el campo de velocidad tiene circulación, es decir, un rizo distinto de cero, si la rueda de paletas gira como se ilustra en la Figura 1-20. El componente de rizo encontrado está en la dirección del eje de la rueda de paletas.

Figura 1-20 Un fluido con un campo de velocidad que tiene un rizo tiende a girar la rueda de paletas. El componente de rizo encontrado está en la misma dirección que el pulgar cuando los dedos de la mano derecha están curvados en la dirección de rotación.

Curl para coordenadas curvilíneas

Se obtiene una definición independiente de coordenadas del rizo usando (7) en (1) como

\[(\nabla \times \textbf{A})_{n} = \lim_{dS_{n} \rightarrow 0} \dfrac{\oint_{L} \textbf{A} \cdot \textbf{dl}}{dS_{n}} \nonumber \]

donde el subíndice n indica el componente del rizo perpendicular al contorno. La derivación de la operación de rizo (8) en coordenadas cilíndricas y esféricas. es sencilla pero larga.

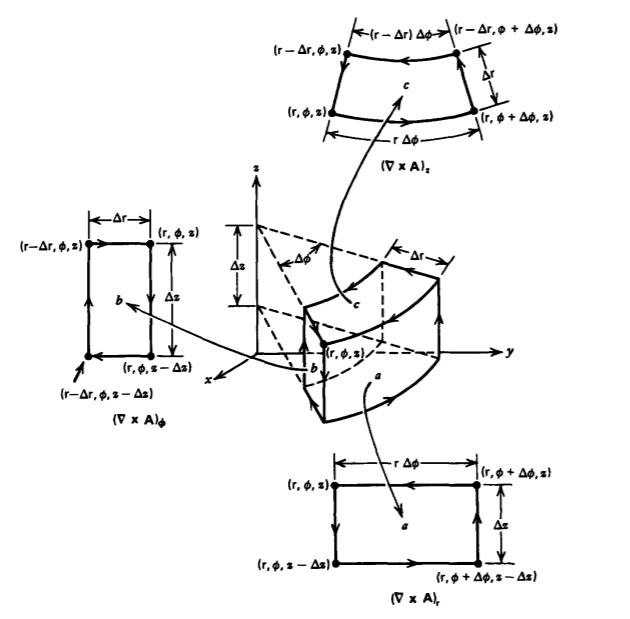
(a) Coordenadas cilíndricas Para expresar cada uno de los componentes del rizo en coordenadas cilíndricas, utilizamos los tres contornos ortogonales de la Figura 1-21. Evaluamos la línea integral alrededor del contorno a:

\[\oint_{a} \textbf{A} \cdot \textbf{dl} = \int_{z}^{z - \Delta z} A_{z}(\phi) dz + \int_{\phi}^{\phi + \Delta \phi} A_{\phi} (z - \Delta z) \textrm{r} \: d \phi \\ + \int_{z - \Delta z}^{z} A_{z} (\phi + \Delta \phi) dz + \int_{\phi + \Delta \phi}^{\phi} A_{\phi} (z) \textrm{r} \: d \phi \\ \approx (\dfrac{[A_{z} (\phi + \Delta \phi) - A_{z} (\phi)]}{\textrm{r} \Delta \phi} - \dfrac{[A_{\phi}(z) - A_{\phi}(z - \Delta z)]}{\Delta z}) \textrm{r} \: \Delta \phi \: \Delta z \nonumber \]

Figura 1-21 Contornos incrementales a lo largo de elementos de área de superficie cilíndrica utilizados para calcular cada componente del rizo de un vector en coordenadas cilíndricas.

para encontrar el componente radial del rizo como

\[(\nabla \times \textbf{A})_{\textrm{r}} = \lim_{\Delta \phi \rightarrow 0 \\ \Delta z \rightarrow 0} \dfrac{\oint_{a} \textbf{A} \cdot \textbf{dl}}{\textrm{r} \: \Delta \phi \: \Delta z} = \dfrac{1}{\textrm{r}} \dfrac{\partial A_{z}}{\partial \phi} - \dfrac{\partial A_{\phi}}{\partial z} \nonumber \]

Evaluamos la línea integral alrededor del contorno b

\[\oint_{b} \textbf{A} \cdot \textbf{dl} = \int_{r-\Delta r}^{r} A_{\textrm{r}}(z) d \textrm{r} + \int_{z}^{z - \Delta z} A_{z}(\textrm{r})dz + \int_{\textrm{r}}^{\textrm{r} - \Delta \textrm{r}} A_{\textrm{r}}(z- \Delta z) d \textrm{r} + \int_{z - \Delta z}^{z} A_{z}(\textrm{r}-\Delta \textrm{r}) dz \\ \approx (\dfrac{[A_{\textrm{r}}(z) - A_{\textrm{r}}(z-\Delta z)]}{\Delta z} - \dfrac{[A_{z}(\textrm{r}) - A_{z}(\textrm{r}- \Delta \textrm{r})]}{\Delta \textrm{r}}) \Delta \textrm{r} \Delta z \nonumber \]

para encontrar el\(\phi\) componente del rizo,

\[(\nabla \times \textbf{A})_{\phi} = \lim_{\Delta \textrm{r} \rightarrow 0 \\ \Delta z \rightarrow 0} \dfrac{\oint_{b} \textbf{A} \cdot \textbf{dl}}{\Delta \textrm{r} \Delta z} = (\dfrac{\partial A_{\textrm{r}}}{\partial z} - \dfrac{\partial A_{z}}{\partial \textrm{r}}) \nonumber \]

El componente z del rizo se encuentra usando el contorno c:

\[\oint_{c} \textbf{A} \cdot \textbf{dl} = \int_{\textrm{r} - \Delta \textrm{r}}^{\textrm{r}} A_{\textrm{r}_{\mid \phi}} d \textrm{r} + \int_{\phi}^{\phi + \Delta \phi} \textrm{r} A_{\phi_{\mid \textrm{r}}} d \phi + \int_{\textrm{r}}^{\textrm{r}- \Delta \textrm{r}} A_{\textrm{r}_{\mid \phi + \Delta \phi}} d \textrm{r} \\ + \int_{\phi + \Delta \phi}^{\phi} (\textrm{r} - \Delta \textrm{r}) A_{\phi_{\mid \textrm{r} - \Delta \textrm{r}}} d \phi \\ \approx (\dfrac{[\textrm{r}A_{\phi_{\mid \textrm{r}}} - (\textrm{r} - \Delta \textrm{r}) A_{\phi_{\mid \textrm{r} - \Delta \textrm{r}}}]}{\textrm{r} \Delta \textrm{r}} - \dfrac{[A_{\textrm{r}_{\mid \phi + \Delta \phi}} - A_{\textrm{r}_{\mid \phi}}]}{\textrm{r} \Delta \phi}) \textrm{r} \Delta \textrm{r} \Delta \phi \nonumber \]

para rendir

\[(\nabla \times \textbf{A})_{z} = \lim_{\Delta \textrm{r} \rightarrow 0 \\ \Delta \phi \rightarrow 0} \dfrac{\oint_{c} \textbf{A} \cdot \textbf{dl}}{\textrm{r} \Delta \textrm{r} \Delta \phi} = \dfrac{1}{\textrm{r}} (\dfrac{\partial}{\partial \textrm{r}} (\textrm{r} A_{\phi}) - \dfrac{\partial A_{\textrm{r}}}{\partial \phi}) \nonumber \]

El rizo de un vector en coordenadas cilíndricas es así

\[\nabla \times \textbf{A} = (\dfrac{1}{\textrm{r}} \dfrac{\partial A_{z}}{\partial \phi} - \dfrac{\partial A_{\phi}}{\partial z})\textbf{i}_{\textrm{r}} + (\dfrac{\partial A_{\textrm{r}}}{\partial z} - \dfrac{\partial A_{z}}{\partial \textrm{r}})\textbf{i}_{\phi} \\ + \dfrac{1}{\textrm{r}} (\dfrac{\partial}{\partial \textrm{r}} (\textrm{r} A_{\phi}) - \dfrac{\partial A_{\textrm{r}}}{\partial \phi})\textbf{i}_{z} \nonumber \]

(b) Coordenadas esféricas

Operaciones similares en los tres contornos incrementales para el elemento esférico en la Figura 1-22 dan el rizo en coordenadas esféricas. Utilizamos el contorno a para el componente radial del rizo:

\[\oint_{a} \textbf{A} \cdot \textbf{dl} = \int_{\phi}^{\phi + \Delta \phi} A_{\phi_{\mid \theta}} r \: \sin \: \theta \: d \phi + \int_{\theta}^{\theta - \Delta \theta} r A_{\theta_{\mid \: \phi + \Delta \phi}} d \theta \\ + \int_{\phi + \Delta \phi}^{\phi} r \: \sin \: (\theta - \Delta \theta)A_{\phi_{\mid \theta - \Delta \theta}} d \phi + \int_{\theta - \Delta \theta}^{\theta} r A_{\theta_{\mid \phi}} d \theta \\ \approx (\dfrac{[A_{\phi_{\mid \theta}} \: \sin \: \theta - A_{\phi_{\mid \theta - \Delta \theta}} \: \sin \: (\theta - \Delta \theta)]}{r \: \sin \: \theta \: \Delta \theta} - \dfrac{[A_{\theta_{\mid \phi + \Delta \phi}} - A_{\theta_{\mid \phi}}]}{r \: \sin \: \theta \: \Delta \phi})r^{2} \: \sin \: \theta \: \Delta \theta \: \Delta \: \phi \nonumber \]

para obtener

\[(\nabla \times \textbf{A})_{r} = \lim_{\Delta \theta \rightarrow 0 \\ \Delta \phi \rightarrow 0} \dfrac{\oint_{a} \textbf{A} \cdot \textbf{dl}}{r^{2} \: \sin \: \theta \: \Delta \theta \: \Delta \phi} = frac{1}{r \: \sin \: \theta}(\dfrac{\partial}{\partial \theta}(A_{\phi} \: \sin \: \theta)- \dfrac{\partial A_{\theta}}{\partial \phi}) \nonumber \]

Figura 1-22 Contornos incrementales a lo largo de elementos de área de superficie esférica utilizados para calcular cada componente del rizo de un vector en coordenadas esféricas.

El\(\theta\) componente se encuentra usando el contorno b:

\[\oint_{b} \textbf{A} \cdot \textbf{dl} = \int_{r}^{r- \Delta r} A_{r_{\mid \phi}} dr + \int_{\phi}^{\phi + \Delta \phi} (r - \Delta r) A_{\phi_{\mid r - \Delta r}} \: \sin \: \theta \: d \phi \\ + \int_{r - \Delta r}^{r} A_{r_{\mid \phi + \Delta phi}} dr + \int_{\phi + \Delta \phi}^{\phi} r A_{\phi_{\mid r}} \: \sin \: \theta \: d \phi \\ \approx (\dfrac{[A_{r_{\mid \phi + \Delta \phi}} - A_{r_{\mid \phi}}]}{r \: \sin \: \theta \: \Delta \phi} - \dfrac{[rA_{\phi_{\mid r}} - (r - \Delta r) A_{\phi_{\mid r - \Delta r}}]}{r \Delta r}) r \: \sin \: \theta \: \Delta r \: \Delta \phi \nonumber \]

\[(\nabla \times A)_{\theta} = \lim_{\Delta r \rightarrow 0 \\ \Delta \phi \rightarrow 0} \dfrac{\oint_{b} \textbf{A} \cdot \textbf{dl}}{r \: \sin \: \theta \: \Delta r \: \Delta \phi} = \dfrac{1}{r} (\dfrac{1}{\sin \: \theta}{\partial A_{r}}{\partial \phi} - \dfrac{\partial}{\partial r}(rA_{phi})) \nonumber \]

El componente 4 del rizo se encuentra usando el contorno c:

\[\oint_{c} \textbf{A} \cdot \textbf{dl} = \int_{\theta - \Delta \theta}^{\theta} rA_{\theta_{\mid r}} d \theta + \int_{r}^{r-\Delta r} A_{r_{\mid \theta}} dr \\ + \int_{\theta}^{\theta - \Delta \theta} (r- \Delta r) A_{\theta_{\mid r- \Delta r}} d \theta + \int_{r - \Delta r}^{r} A_{r_{\mid \theta - \Delta \theta}} dr \\ \approx (\dfrac{[r A_{\theta_{\mid r}} - (r - \Delta r) A_{\theta_{\mid r - \Delta r}}]}{r \Delta r} - \dfrac{[A_{r_{\mid \theta}} - A_{r_{\mid \theta - \Delta \theta}}]}{r \Delta \theta}) r \: \Delta r \: \Delta \theta \nonumber \]

como

\[(\nabla \times \textbf{A})_{\phi} = \lim_{\Delta r \rightarrow 0 \\ \Delta \theta \rightarrow 0} \dfrac{\oint_{c} \textbf{A} \cdot \textbf{dl}}{r \: \Delta r \: \Delta \theta} = \dfrac{1}{r}(\dfrac{\partial}{\partial r} (r A_{\theta}) - \dfrac{\partial A_{r}}{\partial \theta}) \nonumber \]

El rizo de un vector en coordenadas esféricas se da así de (17), (19) y (21) como

\[\nabla \times \textbf{A} = \dfrac{1}{r \: \sin \: \theta} (\dfrac{\partial}{\partial \theta} (A_{\phi} \: \sin \: \theta) - \dfrac{\partial A_{\theta}}{\partial \phi}) \textbf{i}_{r} \\ + \dfrac{1}{r}(\dfrac{1}{\sin \: \theta} \dfrac{\partial A_{r}}{\partial \phi} - \dfrac{\partial}{\partial r}(r A_{\phi}))\textbf{i}_{\theta} \\ + \dfrac{1}{r}(\dfrac{\partial}{\partial r} (r A_{\theta}) - \dfrac{\partial A_{r}}{\partial \theta})\textbf{i}_{\phi} \nonumber \]

Teorema de Stokes

Ahora juntamos muchos contornos de líneas incrementales del tipo utilizado en las Figuras 1-19-1-21 para formar una superficie macroscópica S como las que se muestran en la Figura 1-23. Entonces cada pequeño contorno genera una contribución a la circulación

\[dC = (\nabla \times \textbf{A}) \cdot \textbf{dS} \nonumber \]

para que la circulación total se obtenga por la suma de todos los pequeños elementos superficiales

\[C = \int_{S} (\nabla \times \textbf{A}) \cdot \textbf{dS} \nonumber \]

Figura 1-23 Muchos contornos de línea incrementales distribuidos sobre cualquier superficie, tienen una contribución distinta de cero a la circulación solo a lo largo de aquellas partes de la superficie en el contorno de contorno\(L\).

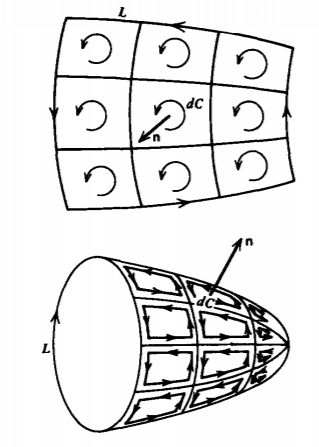
Cada uno de los términos de (23) son equivalentes a la línea integral alrededor de cada contorno pequeño. Sin embargo, todos los contornos interiores comparten lados comunes con contornos adyacentes pero que se recorren dos veces en direcciones opuestas, lo que no produce ninguna contribución integral de línea neta, como se ilustra en la Figura 1-23. Solo aquellos contornos con un lado en el límite abierto L tienen una contribución distinta de cero. El resultado total de sumar las contribuciones para todos los contornos es el teorema de Stokes, que convierte la integral de línea sobre el contorno delimitador L del borde exterior a una integral de superficie sobre cualquier área S delimitada por el contorno

\[\oint_{L} \textbf{A} \cdot \textbf{dl} = \int_{S}(\nabla \times \textbf{A}) \cdot \textbf{dS} \nonumber \]

Tenga en cuenta que hay un número infinito de superficies que están delimitadas por el mismo contorno\(L\). El teorema de Stokes de (25) se satisface para todas estas superficies.

Ejemplo 1-7: TEOREMA DE STOKES

Verificar el teorema de Stokes de (25) para el contorno delimitador circular en el plano xy mostrado en la Figura 1-24 con un vector

campo

Verifique el resultado para la (a) superficie circular plana en el plano xy, (b) para la superficie hemisférica delimitada por el contorno y (c) para la superficie cilíndrica delimitada por el contorno.

Figura 1-24 El teorema de Stokes para el vector dado en el Ejemplo 1-7 se puede aplicar a cualquier superficie que esté limitada por el mismo contorno L.

Solución

Para el contorno mostrado

\[\textbf{dl} = R \: d \phi : \textbf{i}_{\phi}\nonumber \]

para que

\[\textbf{A} \cdot \textbf{dl} = R^{2} d \phi \nonumber \]

donde en L, r = R. Entonces la circulación es

\[C = \oint_{L} \textbf{A} \cdot \textbf{dl} = \int_{0}^{2 \pi} R^{2} \: d \phi = 2 \pi R^{2} \nonumber \]

El componente z de A no tuvo contribución porque dl estaba completamente en el plano xy.

El rizo de A es

\[\nabla \times \textbf{A} = \textbf{i}_{z}(\dfrac{\partial A_{y}}{\partial x} - \dfrac{\partial A_{x}}{\partial y}) = 2 \textbf{i}_{z} \nonumber \]

(a) Para el área circular en el plano del contorno, tenemos que

\[\int_{S} (\nabla \times \textbf{A}) \cdot \textbf{dS} = 2 \int_{S} dS_{z} = 2 \pi R^{2} \nonumber \]

que concuerda con el resultado integral de la línea.

b) Para la superficie hemisférica

\[\int_{S}(\nabla \times \textbf{A}) \cdot \textbf{dS} = \int_{\theta = 0}^{\pi/2} \int_{\phi=0}^{2 \pi} 2 \textbf{i}_{z} \cdot \textbf{i}_{r}R^{2} \: \sin \: \theta \: d \theta \: d \phi \nonumber \]

De la Tabla 1-2 utilizamos la relación de producto punto

\[\textbf{i}_{z} \cdot \textbf{i}_{r} = \cos \: \theta \nonumber \]

que de nuevo da la circulación como

\[C = \int_{\theta = 0}^{\pi/2} \int_{\phi = 0}^{2 \pi} R^{2} \: \sin \: 2 \theta \: d \theta \: d \phi = -2 \pi R^{2} \dfrac{\cos 2 \theta}{2} \bigg|_{\theta = 0}^{\pi/2} = 2 \pi R^{2} \nonumber \]

(c) Del mismo modo, para la superficie cilíndrica, solo obtenemos contribuciones distintas de cero a la integral de superficie en el área circular superior que es perpendicular a\(\nabla \times \textbf{A}\). La integral es entonces la misma que la parte (a) ya que\(\nabla \times \textbf{A}\) es independiente de z.

Algunas identidades vectoriales útiles

Las operaciones de curl, divergencia y gradiente tienen algunas propiedades simples pero útiles que se utilizan a lo largo del texto.

(a) El Curl del Gradiente es Cero

\[\nabla \times (\nabla f)= 0 \nonumber \]

Integramos el componente normal del vector\(\nabla \times (\nabla f)\) sobre una superficie y utilizamos el teorema de Stokes

\[\int_{s} \nabla \times (\nabla f) \cdot \textbf{dS} = \oint_{L} \nabla f \cdot \textbf{dl} = 0 \nonumber \]

donde el resultado cero se obtiene de la Sección 1-3-3, que la integral de línea del gradiente de una función alrededor de una trayectoria cerrada es cero. Dado que la igualdad es verdadera para cualquier superficie, el coeficiente vectorial de dS en (26) debe ser cero

\[\nabla \times (\nabla f) = 0 \nonumber \]

La identidad también se prueba fácilmente mediante cálculo directo usando la relación determinantal en la Sección 1-5-1 que define la operación de rizo:

\[\begin{align*} \nabla \times (\nabla f) &= \det \begin{vmatrix} \textbf{i}_{x} & \textbf{i}_{y} & \textbf{i}_{z} \\ \dfrac{\partial}{\partial x} & \dfrac{\partial}{\partial y} & \dfrac{\partial}{\partial z} \\ \dfrac{\partial f}{\partial x} & \dfrac{\partial f}{\partial y} & \dfrac{\partial f}{\partial z} \end{vmatrix} \\[4pt] &= \textbf{i}_{x} \left(\dfrac{\partial^{2}f}{\partial y \partial z} - \dfrac{\partial^{2} f}{\partial z \partial y}\right) + \textbf{i}_{y} \left(\dfrac{\partial^{2}f}{\partial z \partial x} - \dfrac{\partial ^{2} f}{\partial x \partial x}\right) + \textbf{i}_{z}\left(\dfrac{\partial^{2}f}{\partial x \partial y} - \dfrac{\partial^{2}f}{\partial y \partial x}\right) \\[4pt] &= 0 \end{align*} \nonumber \]

Cada término entre corchetes en (28) es cero porque el orden de diferenciación no importa.

(b) La Divergencia del Curl de un Vector es Cero

\[\nabla - (\nabla \times \textbf{A}) = 0 \nonumber \]

Uno podría estar tentado a aplicar el teorema de divergencia a la integral de superficie en el teorema de Stokes de (25). Sin embargo, el teorema de divergencia requiere una superficie cerrada mientras que el teorema de Stokes es cierto en general para una superficie abierta. El teorema de Stokes para una superficie cerrada requiere que el contorno\(L\) se encoja a cero dando un resultado cero para la integral de línea. El teorema de divergencia aplicado a la superficie cerrada con vector\(\nabla \times \textbf{A}\) es entonces

\[\oint_{S} \nabla \times \textbf{A} \cdot \textbf{dS} = 0 \Rightarrow \int_{V} \nabla \cdot (\nabla \times \textbf{A}) dV = 0 \Rightarrow \nabla \cdot (\nabla \times \textbf{A}) = 0 \nonumber \]

lo que prueba la identidad porque el volumen es arbitrario.

Más directamente podemos realizar las diferenciaciones requeridas

\[\begin{align} \nabla \cdot (\nabla \times \textbf{A}) &= \dfrac{\partial}{\partial x}\left (\dfrac{\partial A_{z}}{\partial y} - \dfrac{\partial A_{y}}{\partial z}\right) + \dfrac{\partial}{\partial y} \left(\dfrac{\partial A_{x}}{\partial z} - \dfrac{\partial A_{z}}{\partial x}\right) + \dfrac{\partial}{\partial z} \left(\dfrac{\partial A_{y}}{\partial x} - \dfrac{\partial A_{x}}{\partial y}\right) \\[4pt] &= \left(\dfrac{\partial^{2} A_{z}}{\partial x \partial y} - \dfrac{\partial^{2} A_{z}}{\partial y \partial x}\right) + \left(\dfrac{\partial^{2}A_{x}}{\partial y \partial z} - \dfrac{\partial^{2}A_{x}}{\partial z \partial y}\right) + \left(\dfrac{\partial^{2}A_{y}}{\partial z \partial x} - \dfrac{\partial^{2}A_{y}}{\partial x \partial z}\right) \\[4pt] &= 0 \end{align} \nonumber \]

donde nuevamente el orden de diferenciación no importa.