2.2: La Ley de Fuerza Coulomb Entre Cargas Estacionarias

Ley de Coulomb

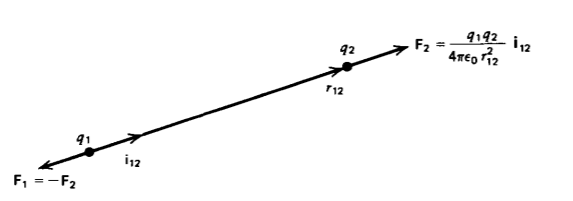
Le quedaba a Charles Coulomb en 1785 expresar estas observaciones experimentales de forma cuantitativa. Utilizó un balance torsional muy sensible para medir la fuerza entre dos bolas cargadas estacionarias en función de su distancia de separación. Descubrió que la fuerza entre dos cargas pequeñas q ₁ y q ₂ (idealizadas como cargas puntuales de tamaño cero) es proporcional a sus magnitudes e inversamente proporcional al cuadrado de la distancia r ₁₂ entre ellas, como se ilustra en la Figura 2-6. La fuerza actúa a lo largo de la línea que une las cargas en la misma dirección o dirección opuesta al vector unitario i ₁₂ y es atractiva si las cargas son de signo opuesto y repulsivas si están como cargadas. La fuerza F ₂ sobre la carga q ₂ debida a la carga q _i es igual en magnitud pero opuesta en dirección a la fuerza _F1 en q ₁, siendo cero la fuerza neta sobre el par de cargas.

\[\textbf{F}_{2} = - \textbf{F}_{1} = \frac{1}{4 \pi \varepsilon_{0}} \frac{q_{1}q_{2}}{r^{2}_{12}} \textbf{i}_{12} \textrm{nt} [\textrm{kg} - \textrm{m} - \textrm{s}^{-2}] \nonumber \]

Unidades

El valor de la constante de proporcionalidad\(1/4 \pi \varepsilon_{0}\) depende del sistema de unidades utilizadas. A lo largo de este libro utilizamos unidades SI (Systeme International d'Unit6s) para las cuales las unidades base se toman del sistema MKSA racionalizado de unidades donde las distancias se miden en metros (m), masa en kilogramos (kg), tiempo en segundos (s) y corriente eléctrica en amperios (A). La unidad de carga es un culombo donde 1 culombio= 1 amperio-segundo. Se utiliza el adjetivo “racionalizado” porque el factor de\(4 \pi\) se introduce arbitrariamente en el factor de proporcionalidad en la ley de Coulomb de (1). Se hace de esta manera para cancelar una\(4 \pi\) que surgirá de otras leyes de uso más frecuente que introduciremos en breve. Otras unidades derivadas se forman combinando unidades base.

Figura 2-6 La fuerza de Coulomb entre dos cargas puntuales es proporcional a la magnitud de las cargas e inversamente proporcional al cuadrado de la distancia entre ellas. La fuerza sobre cada carga es igual en magnitud pero opuesta en dirección. Los vectores de fuerza se dibujan como si q ₁ y q ₂ fueran del mismo signo para que las cargas se repelan. Si q ₁ y q ₂ son de signo opuesto, ambos vectores de fuerza apuntarían en direcciones opuestas, ya que se atraen cargas opuestas.

El parámetro\(\varepsilon_{0}\) se llama la permitividad del espacio libre y tiene un valor

\[\varepsilon_{0} = (4 \pi \times 10^{-7} c^{2})^{-1} \\ \approx \frac{10^{-9}}{36 \pi} \approx 8.8542 \times 10^{-12} \textrm{farad}/\textrm{m} [\textrm{A}^{2} - \textrm{s}^{4} - \textrm{kg}^{-1} - \textrm{m}^{-3}] \nonumber \]

donde c es la velocidad de la luz en vacío (\(c \approx 3 \times 10^{8}\)m/seg).

Esta relación entre la velocidad de la luz y una constante física fue un resultado importante de la teoría electromagnética temprana a finales del siglo XIX, y demostró que la luz es una onda electromagnética; ver la discusión en el Capítulo 7.

Para obtener una idea de cuán grande es la fuerza en (1), la comparamos con la fuerza gravitacional que también es una ley cuadrada inversa con la distancia. La unidad de carga más pequeña conocida es la de un electrón con carga e y masa m _e

\(e \approx 1.60 \times 10^{-19} \: \textrm{Coul}, \: m_{e} \approx 9.11 \times 10^{-31} \textrm{kg}\)

Entonces, la relación de magnitudes de fuerza eléctrica a gravitacional para dos electrones es independiente de su separación:

\[\frac{\textbf{F}_{e}}{\textbf{F}_{g}} = - \frac{e^{2}/(4 \pi \varepsilon_{0} r^{2})}{Gm_{e}^{2}/r^{2}} = - \frac{e^{2}}{m_{e}^{2}} \frac{1}{4 \pi \varepsilon_{0}G} \approx - 4.16 \times 10^{42} \nonumber \]

donde\(G = 6.67 \times 10^{-11} [\textrm{m}^{3} - \textrm{s}^{-2} - \textrm{kg}^{-1}]\) está la constante gravitacional. Esta relación es tan grande que ejemplifica por qué las fuerzas eléctricas suelen dominar los fenómenos físicos. El signo menos se usa en (3) porque la fuerza gravitacional entre dos masas siempre es atractiva mientras que para dos cargas similares la fuerza eléctrica es repulsiva.

Campo Eléctrico

Si la carga q ₁ existe sola, no siente fuerza. Si ahora traemos la carga q ₂ dentro de las proximidades de q ₁, entonces q ₂ siente una fuerza que varía en magnitud y dirección a medida que se mueve en el espacio y es así una forma de mapear el campo de fuerza vectorial debido a q ₁ . Una carga distinta a q ₂ sentiría una fuerza diferente de q ₂ proporcional a su propia magnitud y signo. Se vuelve conveniente trabajar con la cantidad de fuerza por unidad de carga que se llama campo eléctrico, ya que esta cantidad es independiente del valor particular de carga utilizado para mapear el campo de fuerza. Considerando q ₂ como la carga de prueba, el campo eléctrico debido a q ₁ en la posición de q ₂ se define como

\[\textrm{E}_{2} = \lim_{q_{2} \rightarrow 0} \frac{\textbf{F}_{2}}{q_{2}} = \frac{q_{1}}{4 \pi \varepsilon_{0} r^{2}_{12}} \textbf{i}_{12} \textrm{volts}/ \textrm{12} [\textrm{kg} - \textrm{m} - \textrm{s}^{-3} - \textrm{A}^{-1}] \nonumber \]

En la definición de (4) la carga q ₁ debe permanecer estacionaria. Esto requiere que la carga de prueba q ₂ sea despreciablemente pequeña para que su fuerza sobre q ₁ no haga que q ₁ se mueva. En presencia de materiales cercanos, la carga de prueba q ₂ también podría inducir o provocar la redistribución de las cargas en el material. Para evitar estos efectos en nuestra definición del campo eléctrico, hacemos que la carga de prueba sea infinitamente pequeña por lo que sus efectos sobre los materiales y cargas cercanas también son insignificantemente pequeños. Entonces (4) también será una definición válida del campo eléctrico cuando consideremos los efectos de los materiales. Para mapear correctamente el campo eléctrico, la carga de prueba no debe alterar la distribución de carga de lo que es en ausencia de la carga de prueba.

Superposición

Si nuestro sistema solo consta de dos cargas, la ley de Coulomb (1) describe completamente su interacción y la definición de campo eléctrico es innecesaria. El concepto de campo eléctrico sólo es útil cuando hay grandes cantidades de carga presentes ya que cada carga ejerce una fuerza sobre todas las demás. Dado que las fuerzas sobre una carga en particular son lineales, podemos usar superposición, por lo que si una carga q ₁ sola configura un campo eléctrico E ₁, y otra carga q ₂ sola da lugar a un campo eléctrico E ₂, entonces el campo eléctrico resultante con ambas cargas presentes es la suma vectorial E ₁ + E ₂. Esto significa que si se coloca una carga de prueba q _p en el punto P de la Figura 2-7, en las proximidades de N cargas se sentirá una fuerza

\[\textbf{F}_{p} = q_{p} \textbf{E}_{P} \nonumber \]

Figura 2-7 El campo eléctrico debido a una colección de cargas puntuales es igual a la suma vectorial de campos eléctricos de cada carga sola.

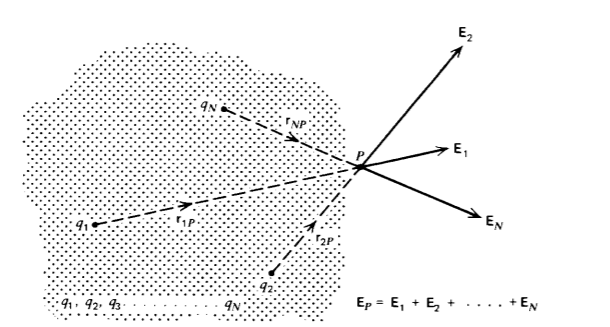
donde E _P es la suma vectorial de los campos eléctricos debido a todas las cargas de N puntos,

\[\textbf{E}_{P} = \frac{1}{4 \pi \varepsilon_{0}} (\frac{q_{1}}{r_{1P}^{2}} + \frac{q_{2}}{r_{2P}^{2}}\textbf{i}_{2P} + \frac{q_{3}}{r_{3P}^{2}} \textbf{i}_{3P} + ... +\frac{q_{N}}{r_{NP}^{2}} \textbf{i}_{NP}) = \frac{1}{4 \pi \varepsilon_{0}} \sum_{n = 1}^{N} \frac{q_{n}}{r^{2}_{nP}} \textbf{i}_{nP} \nonumber \]

Tenga en cuenta que E _P no tiene contribución debido a q _p ya que una carga no puede ejercer una fuerza sobre sí misma.

Ejemplo 2-1: Cargos de dos puntos

Las cargas de dos puntos están separadas a lo largo del eje z como se muestra en la Figura 2-8. Encuentra el campo eléctrico en cualquier punto del plano z =0 cuando las cargas son:

(a) ambos iguales a q

(b) de polaridad opuesta pero igual magnitud ±q. Esta configuración se denomina dipolo eléctrico.

Solución

(a) En el plano z =0, cada carga puntual por sí sola da lugar a componentes de campo en las direcciones i _r e _iz. Cuando ambas cargas son iguales, la superposición de componentes de campo debido a ambas cargas se cancela en la dirección z pero agrega radialmente:

\(E_{\textrm{r}}(z= 0) = \frac{q}{4 \pi \varepsilon_{0}} \frac{2 \textrm{r}}{[\textrm{r}^{2} + (a/2)^{2}]^{3/2}}\)

Como nota de verificación que lejos de los cargos puntuales (r >> a) el campo se acerca al de una carga puntual de valor 2 q:

\(\lim_{r >>a} E_{\textrm{r}(z = 0) = \frac{2q}{4 \pi \varepsilon_{0}\textrm{r}^{2}}\)

(b) Cuando las cargas tienen polaridad opuesta, el campo eléctrico total debido a ambas cargas ahora se cancela en la dirección radial pero se suma en la dirección z:

\(E_{z}(z=0) = \frac{-q}{4 \pi \varepsilon_{0}} \frac{a}{[\textrm{r}^{2} + (a/2)^{2}]^{3/2}}\)

Lejos del punto se carga el campo eléctrico muere como el cubo inverso de distancia:
\(\lim_{r >> a} E_{z} (z = 0) = \frac{-qa}{4 \pi \varepsilon_{0}\textrm{r}^{3}}\)

Figura 2-8 Dos cargas puntuales de igual magnitud están separadas a una distancia a a lo largo del eje z. (a) Cuando las cargas sean de la misma polaridad, el campo eléctrico debido a cada una se aleja radialmente. En el plano de simetría z = 0, el componente de campo neto es radial. (b) Cuando las cargas son de polaridad opuesta, el campo eléctrico debido a la carga negativa se dirige radialmente hacia adentro. En el plano de simetría z = 0, el campo neto es ahora - z dirigido.

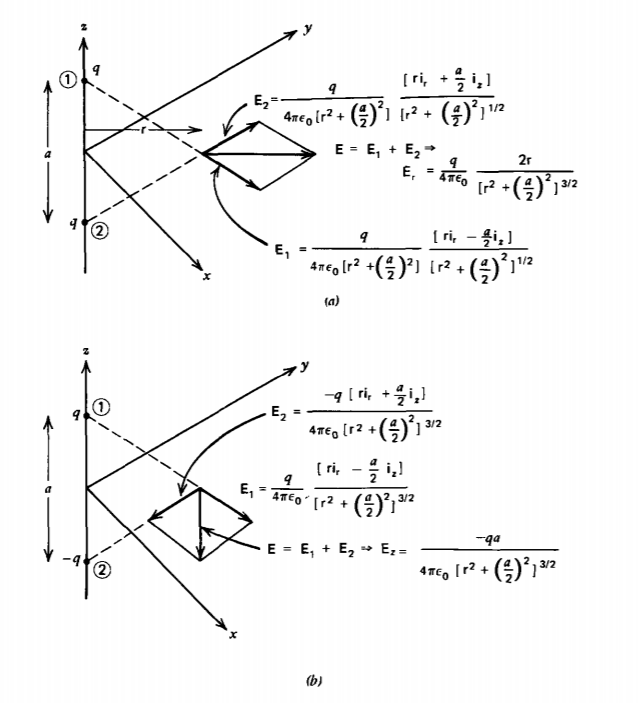
La tasa más rápida de decaimiento de un campo dipolar se debe a que la carga neta es cero, por lo que los campos debidos a cada carga tienden a cancelarse entre sí.