2.3: Distribuciones de carga

El método de superposición utilizado en la Sección 2.2.4 se utilizará a lo largo del texto para relacionar campos con sus fuentes. Primero encontramos el campo debido a una fuente de un solo punto. Debido a que las ecuaciones de campo son lineales, el campo neto debido a muchas fuentes puntuales es solo la superposición de los campos de cada fuente sola. Así, conocer el campo eléctrico para una carga de un solo punto, en una posición arbitraria, inmediatamente nos da el campo total para cualquier distribución de cargas puntuales.

En situaciones típicas, un culombo de carga total puede estar presente requiriendo 6.25 x 10 ¹⁸ cargas elementales (e ≈1.60 x 10 ^-19 coul). Cuando se trata de un número tan grande de partículas, la naturaleza discreta de las cargas a menudo no es importante y podemos considerarlas como un continuo. Luego podemos describir la distribución de carga por su densidad. El mismo modelo se utiliza en el tratamiento clásico de la materia. Cuando hablamos de masa no vamos a la escala molecular y contamos el número de moléculas, sino que describimos el material por su densidad de masa que es el producto del número promedio local de moléculas en una unidad de volumen y la masa por molécula.

Distribuciones de carga de línea, superficie y volumen

De igual manera hablamos de densidades de carga. Las cargas pueden distribuirse en una línea con densidad de carga de línea\(\lambda\) (coul/m), en una superficie con densidad de carga superficial\(\sigma\) (coul/m ²) o a lo largo de un volumen con densidad de carga volumétrica\(\rho\) (coul/m ³)

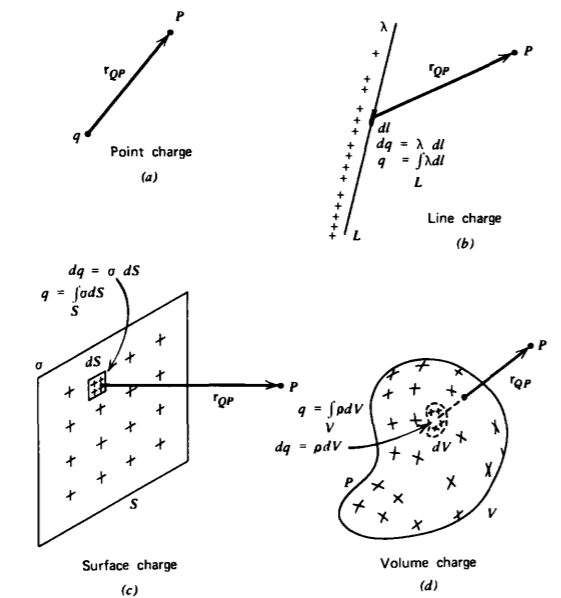
Considere una distribución de dq de carga libre de tamaño diferencial dentro de una distribución macroscópica de carga de línea, superficie o volumen como se muestra en la Figura 2-9. Entonces, la carga total q dentro de cada distribución se obtiene sumando todos los elementos diferenciales. Esto requiere una integración sobre la línea, superficie o volumen ocupado por la carga.

\[dq = \left\{ \begin{array}{ll} \lambda dl \\ \sigma \: dS \Rightarrow q = \\ \rho \: d V \end{array} \right. \left \{ \begin{array}{ll} \int_{l} \lambda \: dl \: \textrm{(line charge)} \\ \int_{S} \sigma \: dS \: \textrm{(surface charge)} \\ \int_{V} \rho \: dV \: \textrm{(volume charge)} \end{array} \right. \nonumber \]

Ejemplo 2-2: Distribución de carga

Encuentre el cargo total dentro de cada una de las siguientes distribuciones ilustradas en la Figura 2-10

(a) Carga de línea distribuida\(\lambda_{0}\) uniformemente en un aro circular de radio a.

Figura 2-9 Distribuciones de carga. a) Carga puntual; b) Carga de línea; c) Carga superficial; d) Carga por volumen.

(b) Carga superficial distribuida\(\sigma_{0}\) uniformemente sobre un disco circular de radio a.

(c) Carga volumétrica distribuida\(\rho_{0}\) uniformemente a lo largo de una esfera de radio R.

Figura 2-10 Distribuciones de carga del Ejemplo 2-2. (a) Carga de línea uniformemente distribuida en un aro circular. (b) Carga superficial uniformemente distribuida sobre un disco circular. c) Carga volumétrica uniformemente distribuida a lo largo de una esfera. d) Distribución no uniforme de carga por línea. e) Suave distribución de carga volumétrica dependiente radialmente a lo largo de todo el espacio, como un modelo simple de la nube de electrones alrededor del núcleo cargado positivamente del átomo de hidrógeno.

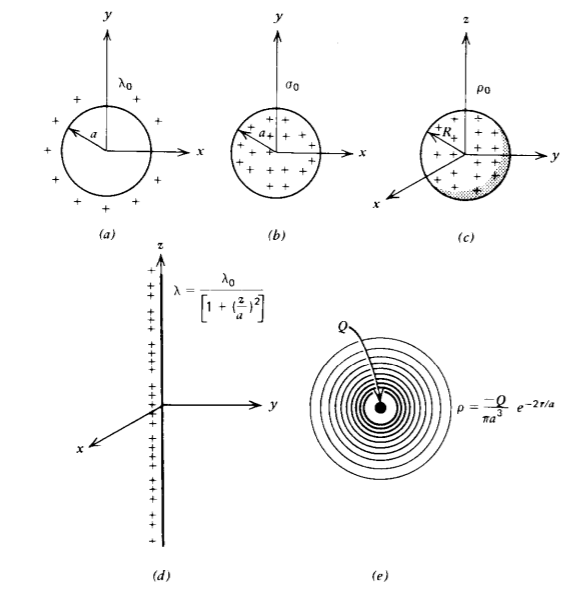
(d) Una carga lineal de extensión infinita en la dirección z con distribución de densidad de carga

\(\lambda = \frac{\lambda_{0}}{[1 + (z/a)^{2}]}\)

e) La nube de electrones alrededor del núcleo Q cargado positivamente en el átomo de hidrógeno se modela simplemente como la distribución esféricamente simétrica

\(\rho(r) = \frac{Q}{\pi a^{3}} e^{-2r/a}\)

Solución

(a)\(q = \int_{L} \lambda \: dl = \int_{0}^{2 \pi} \lambda_{0}a \: d \phi = 2 \pi a \lambda_{0}\)

b)\(q = \int_{S} \sigma d \textrm{S} = \int_{\textrm{r} = 0}^{2 \pi} \sigma_{0} \textrm{r} d \textrm{r} \: d \pi a^{2} \sigma_{0}\)

c)\(q = \int_{V} \rho \: dV = \int_{r = 0}^{R} \int_{\theta = 0}^{\pi} \int_{\phi 0}^{2 \pi} \rho_{0}r^{2} \sin \: \theta dr \: d \theta \: d \phi = \frac{4}{3} \pi R^{3} \rho_{0}\)

d)\(q = \int_{L} \lambda \: dl = \int_{- \infty}^{+ \infty} \frac{\lambda_{0} dz}{[1 + (z/a)^{2}]} = \lambda_{0}a \: \tan^{-1} \frac{z}{a} \bigg|_{- \infty}^{+ \infty} = \lambda_{0}\pi a\)

El cargo total en la nube es

\(q = \int_{V} \rho \: dV \\ = -\int_{r = 0}^{\infty} \int_{\theta = 0}^{\pi} \int_{\phi = 0}^{2 \pi} \frac{Q}{\pi a^{3}} e^{-2r/a} r^{2} \sin \: \theta \: dr \: d \theta \: d \phi \\ = -\int_{r = 0}^{\infty} \frac{4Q}{a^{3}}e^{-2r/a} r^{2} \: dr \\ = -\frac{4Q}{a^{3}} (- \frac{a}{2}) e^{-2r/a} [r^{2} - \frac{a^{2}}{2}(-\frac{2r}{a} -1)] \bigg|_{r = 0}^{\infty} \\ = -Q\)

Campo eléctrico debido a una distribución de carga

Cada elemento de carga diferencial dq como fuente en el punto Q contribuye al campo eléctrico en un punto P como

\[d \textbf{E} = \frac{dq}{4 \pi \varepsilon_{0} r^{2}_{QP}} \textbf{i}_{QP} \nonumber \]

donde r _QP es la distancia entre Q y P con i _QP el vector unitario dirigido de Q a P. Para encontrar el campo eléctrico total, es necesario resumir las contribuciones de cada elemento de carga. Esto equivale a integrar (2) en toda la distribución de carga, recordando que tanto la distancia r _QP como la dirección i _QP varían para cada elemento diferencial a lo largo de la distribución

\[\textbf{E} = \int_{\textbf{all} \: q} \frac{dq}{4 \pi \varepsilon_{0}r_{QP}^{2}} \textbf{i}_{QP} \nonumber \]

donde (3) es una integral de línea para cargas de línea (\(dq = \lambda \: dl\)), una integral de superficie para cargas superficiales (\(dq = \sigma \: dS\)), una integral de volumen para una distribución de carga volumétrica (\(dq = \rho \: dV\)), o en general, una combinación de las tres.

Si se conoce la distribución total de la carga, el campo eléctrico se obtiene realizando la integración de (3). Algunas reglas generales y sugerencias al usar (3) son:

1. Es necesario distinguir entre las coordenadas de los puntos de campo y los puntos de origen de carga. Siempre integre sobre las coordenadas de las cargas.
2. La ecuación (3) es una ecuación vectorial y por lo tanto generalmente tiene tres componentes que requieren tres integraciones. Los argumentos de simetría a menudo se pueden usar para mostrar que los componentes de campo particulares son cero.
3. La distancia r _QP es siempre positiva. Al tomar raíces cuadradas, asegúrese siempre de que se tome la raíz cuadrada positiva.
4. La solución a un problema particular a menudo se puede obtener integrando las contribuciones de estructuras diferenciales de tamaño más simples.

Campo debido a una carga de línea infinitamente larga

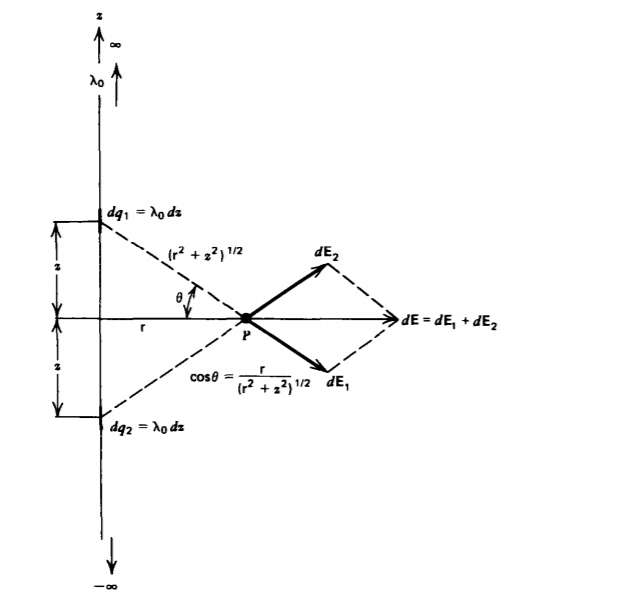
En la Figura 2-11 se muestra una carga lineal uniformemente distribuida infinitamente larga a\(\lambda_{0}\) lo largo del eje z. Considere los dos elementos de carga ubicados simétricamente dq ₁ y dq ₂ a una distancia z por encima y por debajo del punto P, una distancia radial r de distancia. Cada elemento de carga por sí solo aporta componentes radiales y z al campo eléctrico. Sin embargo, tal como encontramos en el Ejemplo 2-1a, los dos elementos de carga juntos causan componentes de campo z de igual magnitud pero dirigidos opuestamente que, por lo tanto, cancelan dejando solo componentes radiales aditivos:

\[dE_{\textrm{r}} = \frac{\lambda_{0} dz}{4 \pi \epsilon_{0}(z^{2} + \textrm{r}^{2})} \cos \: \theta = \frac{\lambda_{0} \textrm{r} dz}{4 \pi \varepsilon_{0}(z^{2} + \textrm{r}^{2})^{3/2}} \nonumber \]

Para encontrar el campo eléctrico total integramos a lo largo de la carga de la línea:

\[E_{\textrm{r}} = \frac{\lambda_{0} \textrm{r}}{4 \pi \varepsilon_{0}} \int_{- \infty}^{+ \infty} \frac{dz}{(z^{2} + \textrm{r}^{2})^{3/2}} \\ = \frac{\lambda_{0} \textrm{r}}{4 \pi \varepsilon_{0}} \frac{z}{\textrm{r}^{2}(z^{2} + \textrm{r}^{2})^{1/2}} \bigg|_{z = - \infty}^{+ \infty} \\ = \frac{\lambda_{0}}{2 \pi \varepsilon_{0} \textrm{r}} \nonumber \]

Figura 2-8a.

Campo debido a infinitas hojas de carga superficial

(a) Hoja Única

Una hoja de carga superficial de extensión infinita en el plano y =0 tiene una densidad de carga superficial uniforme\(\sigma_{0}\) como en la Figura 2-12 a. Rompemos la lámina en muchas cargas de línea incrementales de espesor dx con\(d \lambda = \sigma_{0} dx\). Podríamos romper la superficie de manera equivalente en cargas de línea horizontales incrementales de espesor dz. Cada carga de línea incremental por sí sola tiene un componente de campo radial dado por (5) que en coordenadas cartesianas da como resultado componentes x e y. Considera la carga de línea\(d \lambda_{1}\), una distancia x a la izquierda de P y la carga de línea colocada simétricamente a\(d \lambda_{2}\) la misma distancia x a la derecha de P. Los componentes x de los campos resultantes se cancelan mientras que el y

Figura 2-12 (a) El campo eléctrico de una lámina cargada uniformemente en superficie de extensión infinita se encuentra sumando las contribuciones de cada elemento de carga de línea incremental. Los elementos de carga de línea colocados simétricamente tienen componentes de x campo que cancelan, pero y componentes de campo que agregan. (b) Dos hojas de carga superficial paralelas pero con carga opuesta tienen campos que se agregan en la región entre las hojas pero cancelan afuera. c) El campo eléctrico de una distribución de carga volumétrica se obtiene sumando las contribuciones de cada elemento de carga superficial incremental

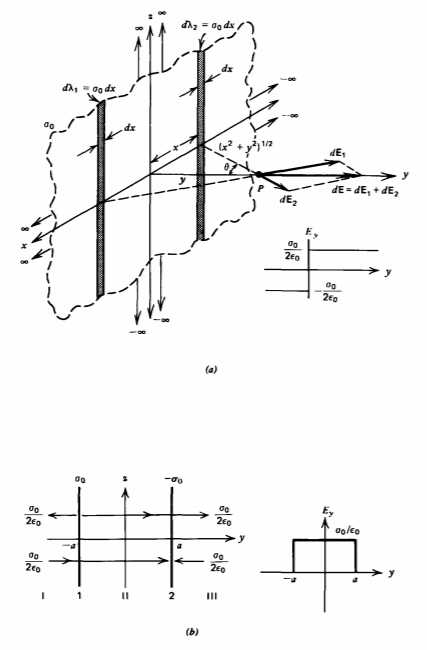
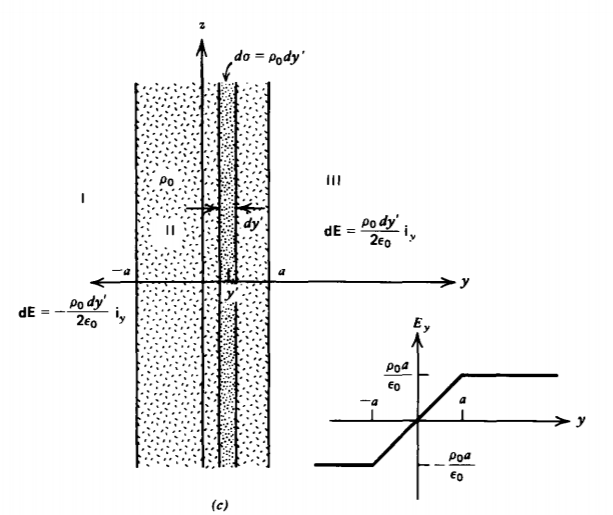
Fig. 2-12 (c)

componentes add:

\[dE_{y} = \frac{\sigma_{0}dx}{2 \pi \varepsilon_{0}(x^{2} + y^{2})^{1/2}} \cos \: \theta = \frac{\sigma_{0}y \: dx}{2 \pi \varepsilon_{0}(x^{2} + y^{2})} \nonumber \]

El campo total se obtiene entonces por integración sobre todos los elementos de carga de línea:

\[E_{y} = \frac{\sigma_{0}y}{2 \pi \varepsilon_{0}} \int_{- \infty}^{+ \infty} \frac{dx}{x^{2} + y^{2}} \\ \frac{\sigma_{0}y}{2 \pi \varepsilon_{0}} \frac{1}{y} \tan^{-1} \frac{x}{y} \bigg|_{x = - \infty}^{+ \infty} \\ = \left \{ \begin{matrix} \sigma_{0}/2 \varepsilon_{0}, & y>0 \\ -\sigma_{0}/2 \varepsilon_{0}, & y<0 \end{matrix} \right. \nonumber \]

donde nos dimos cuenta de que el término tangente inverso toma el signo de la relación x/y para que el campo revierta la dirección en cada lado de la hoja. La intensidad de campo no disminuye con la distancia desde la hoja infinita

(b) Hojas Paralelas de Signo Opuesto

Un condensador está formado por dos láminas de carga superficial cargadas opuestamente a una distancia 2a como se muestra en la Figura 2-12b.

Los campos debidos solo a cada hoja cargada se obtienen de (7) como

\[\textbf{E}_{1} = \left \{ \begin{matrix} \frac{\sigma_{0}}{2 \varepsilon_{0}} \textbf{i}_{y}, & y > -a \\ -\frac{\sigma_{0}}{2 \varepsilon_{0}} \textbf{i}_{y}, & y < -a \end{matrix} \right. \textbf{E}_{2} = \left \{ \begin{matrix} -\frac{\sigma_{0}}{2 \varepsilon_{0}} \textbf{i}_{y}, & y>a \\ \frac{\sigma_{0}}{2 \varepsilon_{0}} \textbf{i}_{y}, & y < a \end{matrix} \right. \nonumber \]

De esta manera, fuera de las hojas en las regiones I y III los campos cancelan mientras que agregan en la región cerrada II. El campo distinto de cero se limita a la región entre las hojas cargadas y es independiente del espaciado:

\[\textbf{E} = \textbf{E}_{1} + \textbf{E}_{2} = \left \{ \begin{matrix} (\sigma_{0}/\varepsilon_{0}) \textbf{i}_{y}, & \vert y \vert < a \\ 0 & \vert y \vert > a \end{matrix} \right. \nonumber \]

(c) Volumen uniformemente cargado

Un volumen cargado uniformemente con densidad\(\rho_{0}\) de carga de extensión infinita en las direcciones x y z y de ancho 2a está centrado alrededor del eje y, como se muestra en la Figura 2-12c. Rompimos la distribución de volumen en hojas incrementales de carga superficial de ancho dy' con densidad de carga superficial diferencial\(d \sigma = \rho_{0} d y'\). Es necesario distinguir la posición y' de la lámina diferencial de carga superficial del punto de campo y. El campo eléctrico total es la suma de todos los campos debido a cada hoja cargada diferencialmente. El problema se descompone en tres regiones. En la región I, donde\(y \leq -a\), cada elemento de carga superficial provoca un campo en la dirección y negativa:

\[E_{y} = \int_{-a}^{a} - \frac{\rho_{0}}{2 \varepsilon_{0}} d y' = -\frac{\rho_{0}a}{\varepsilon_{0}}, \: \: y \leq -a \nonumber \]

De igual manera, en la región III, donde\(y \geq a\) y a, cada hoja cargada da lugar a un campo en la dirección y positiva:

\[E_{y} = \int_{-a}^{a} \frac{\rho_{0}dy'}{2 \varepsilon_{0}} = \frac{\rho_{0} d y'}{2 \varepsilon_{0}} = \frac{\rho_{0}a}{\varepsilon_{0}}, \: \: y \geq a \nonumber \]

Para cualquier posición y en la región II, donde\(-a \leq y \leq a\), la carga a la derecha de y da lugar a un campo dirigido negativamente mientras que la carga a la izquierda de y provoca un campo dirigido positivamente:

\[E_{y} = \int_{-a}^{y} \frac{\rho_{0}dy'}{2 \varepsilon_{0}} + \int_{y}^{a} (-) \frac{ \rho_{0}}{2 \varepsilon_{0}} dy' = \frac{\rho_{0} y}{\varepsilon_{0}'} \: -a \leq y \leq a \nonumber \]

El campo es así constante fuera del volumen de carga y en direcciones opuestas a cada lado siendo el mismo que para una lámina cargada en superficie con la misma carga total por unidad de área,\(\sigma_{0} = \rho_{0} 2a\). En los límites\(y = \pm a\), el campo es continuo, cambiando linealmente con la posición entre los límites:

\[\textbf{E}_{y} = \left \{ \begin{matrix} -\frac{\rho_{0}a}{\varepsilon_{0}}, & y \leq -a \\ \frac{\rho_{0}y}{\varepsilon_{0}}, & -a \leq y \leq a \\ \frac{\rho_{0}a}{\varepsilon_{0}}, & y \geq a \end{matrix} \right. \nonumber \]

Superposición de Aros de Carga de Línea

(a) Aro único

Usando superposición, podemos construir soluciones de manera similar a partir de un aro circular de radio a con densidad de carga lineal uniforme\(\lambda_{0}\) centrada alrededor del origen en el plano z = 0 como se muestra en la Figura 2-13a. A lo largo del eje z, la distancia al perímetro del aro\((a^{2} + z^{2})^{1/2}\) es la misma para todos los elementos de carga puntual incremental\(dq = \lambda_{0}a \: d \phi\). Cada elemento de carga por sí solo aporta componentes de campo eléctrico dirigidos z y r. Sin embargo, a lo largo del eje z, los elementos colocados simétricamente separados 180° tienen componentes z que agregan pero componentes radiales que cancelan. El campo eléctrico dirigido por z a lo largo del eje z es entonces

\[\textbf{E}_{z} = \int_{0}^{2 \pi} \frac{\lambda_{0}a \: d \phi \: \cos \theta}{4 \pi \varepsilon_{0}(z^{2} + a^{2})} = \frac{ \lambda_{0} az}{2 \varepsilon_{0}(a^{q} + z^{2})^{3/2}} \nonumber \]

El campo eléctrico está en la dirección - z a lo largo del eje z debajo del aro.

La carga total en el aro es\(q = 2 \pi a \lambda_{0}\) para que (14) también se pueda escribir como

\[E_{z} = \frac{qz}{4 \pi \varepsilon_{0}(a^{2} + z^{2})^{3/2}} \nonumber \]

Cuando nos alejamos del aro (\(\vert z \vert >> a\)), el campo se acerca al de una carga puntual:

\[\lim_{\vert z \vert >> a} \: E_{z} = \pm \frac{q}{4 \pi \varepsilon_{0}z^{2}} \left \{ \begin{matrix} z>0 \\ z< 0 \end{matrix} \right. \nonumber \]

(b) Disco de carga superficial

La solución para un disco circular de carga superficial uniformemente distribuida\(\sigma_{0}\) se obtiene rompiendo el disco en aros incrementales de radio r con carga de línea\(d \lambda = \sigma_{0} d \) r como en

Figura 2-13 (a) El campo eléctrico a lo largo del eje z de simetría de un aro de carga lineal distribuido uniformemente se dirige z. b) El campo axial de un disco circular de carga superficial se obtiene sumando radialmente las contribuciones de los aros incrementales de carga de línea. c) El campo axial de un cilindro hueco de carga superficial se obtiene sumando axialmente las contribuciones de los aros incrementales de carga de línea. d) El campo axial de un cilindro de carga volumétrica se encuentra sumando las contribuciones de discos incrementales axiales o de cilindros huecos radiales de carga superficial.

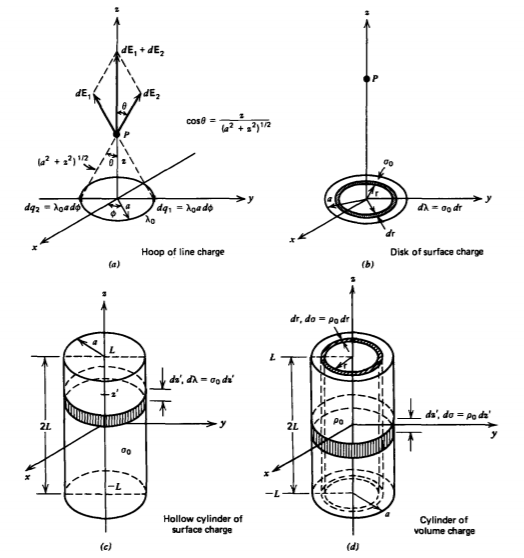
Figura 2-13b. Luego, el campo eléctrico incremental dirigido por z a lo largo del eje z debido a un aro de radio r se encuentra de (14) como

\[dE_{z} = \frac{\sigma_{0} \textrm{r} z \: d \textrm{r}}{2 \varepsilon_{0} (\textrm{r}^{2} + z^{2})^{3/2}} \nonumber \]

donde reemplazamos a por r, el radio del aro incremental. El campo eléctrico total es entonces

\[E_{z} = \frac{\sigma_{0}z}{2 \varepsilon_{0}} \int-{0}^{a} \frac{\textrm{r} d \textrm{r}}{(\textrm{r}^{2} + z^{2})^{3/2}} \\ = - \frac{\sigma_{0}z}{2 \varepsilon_{0}(\textrm{r}^{2} + z^{2})^{1/2}} \bigg|_{0}^{a} \\ = -\frac{\sigma_{0}}{2 \varepsilon_{0}} (\frac{z}{(a^{2} + z^{2})^{1/2}} - \frac{z}{\vert z \vert}) \\ = \pm \frac{\sigma_{0}}{2 \varepsilon_{0}} - \frac{\sigma_{0}z}{2 \varepsilon_{0}(a^{2} + z^{2})^{1/2}} \left \{ \begin{matrix} z > 0 \\ z< 0 \end{matrix} \right. \nonumber \]

donde se tuvo cuidado en el límite inferior (r = 0), ya que siempre se debe utilizar la magnitud de la raíz cuadrada.

A medida que el radio del disco se vuelve muy grande, este resultado se acerca al del campo uniforme debido a una hoja infinita de carga superficial:

\[\lim_{a \rightarrow \infty} E_{z} = \pm \frac{\sigma_{0}}{2 \varepsilon_{0}} \left \{ \begin{matrix} z > 0 \\ z < 0 \end{matrix} \right. \nonumber \]

(c) Cilindro hueco de carga superficial

Un cilindro hueco de longitud 2 L y radio a tiene su eje a lo largo de la dirección z y está centrado alrededor del plano z =0 como en la Figura 2-13 c. Su superficie exterior en r= a tiene una distribución uniforme de la carga superficial\(\sigma_{0}\). Es necesario distinguir entre la coordenada del punto de campo z y el punto de origen en z '(\(-L \leq z' \leq L\)). El cilindro hueco se divide en aros incrementales de carga de línea\(d \lambda = \sigma_{0} dz'\). Entonces, la distancia axial desde el punto de campo en z hasta cualquier aro incremental de carga de línea es (z - z'). La contribución al campo eléctrico axial en z debido al aro incremental en z' se encuentra en (14) as'

\[dE_{z} = \frac{\sigma_{0}a(z-z') dz'}{2 \varepsilon_{0}[a^{2} + (z-z')^{2}]^{3/2}} \nonumber \]

que cuando se integra sobre la longitud del cilindro rinde

\[E_{z} = \frac{\sigma_{0}a}{2 \varepsilon_{0}} \int_{-L}^{+L} \frac{(z-z') dz'}{[a^{2} + (z-z')^{2}]^{3/2}} \\ = \frac{\sigma_{0}a}{2 \varepsilon_{0}} \frac{1}{[a^{2} + (z - z')^{2}]^{1/2}} \bigg|_{z' = -L}^{+L} \\ = \frac{\sigma_{0}a}{2 \varepsilon_{0}} (\frac{1}{[a^{2} + (z-L)^{2}]^{1/2}} - \frac{1}{[a^{2} + (z + L)^{2}]^{1/2}}) \nonumber \]

(d) Cilindro de carga volumétrica

Si este mismo cilindro se carga uniformemente en todo el volumen con densidad de carga\(\rho_{0}\), se rompe el volumen en cilindros huecos de tamaño diferencial de espesor d r con carga superficial incremental\(d \sigma = \rho_{0} d\) r como en la Figura 2-13 d. Luego, el campo eléctrico dirigido z a lo largo del eje z se obtiene mediante la integración de (21) reemplazando a por r:

\[E_{z} = \frac{\rho_{0}}{2 \varepsilon_{0}} \int_{0}^{a} \textrm{r}(\frac{1}{[\textrm{r}^{2} + (z - L)^{2}]^{1/2}} - \frac{1}{[\textrm{r}^{2} + (z + L)^{2}]^{1/2}}) d \textrm{r} \\ = \frac{\rho_{0}}{2 \varepsilon_{0}} \{[\textrm{r}^{2} + (z-L)^{2}]^{1/2} - [\textrm{r}^{2} + (z+L)^{2}]^{1/2} \} \bigg|_{0}^{a} \\ = \frac{\rho_{0}}{2 \varepsilon_{0}} \{[a^{2} + (z-L)^{2}]^{1/2} - \vert z - L \vert - [a^{2} + (z+L)^{2}]^{1/2} \\ + \vert z + L \vert \} \nonumber \]

donde en el límite inferior r=0 siempre tomamos la raíz cuadrada positiva.

Este problema podría haberse resuelto igualmente bien rompiendo la distribución de carga de volumen en muchos discos con carga superficial de tamaño diferencial en la posición z' (\(-L \leq z' \leq L\)), espesor dz' y densidad de carga superficial efectiva\(d \sigma = \rho_{0} dz'\). El campo se obtiene entonces integrando (18).