2.4: Ley de Gauss

Podríamos continuar construyendo soluciones para distribuciones de carga dadas usando la integral de superposición de culombo de la Sección 2.3.2. Sin embargo, para geometrías con simetría espacial, a menudo hay una manera más simple usando algunas propiedades vectoriales de la ley cuadrada inversa dependencia del campo eléctrico.

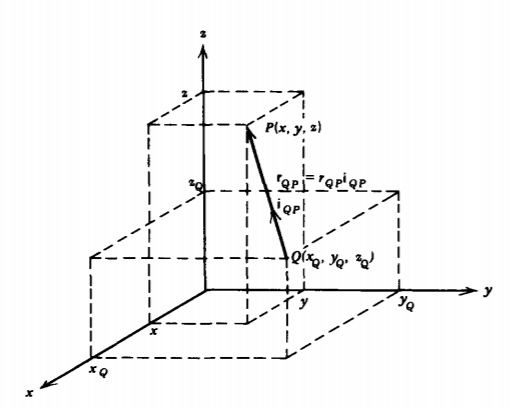
Propiedades del Vector Distancia Entre Dos Puntos, r _QP

(a) r _QP

En las coordenadas cartesianas, la distancia vectorial r _QP entre un punto de origen en Q y un punto de campo en P dirigido de Q a P como se ilustra en la Figura 2-14 es

\[\textbf{r}_{QP} = (x - x_{Q})\textbf{i}_{x} + (y - y_{q})\textbf{i}_{y} + (z-z_{Q})\textbf{i}_{z} \nonumber \]

con magnitud

\[r_{QP} = [(x - x_{Q})^{2} + (y - y_{Q})^{2} + (z - z_{Q})^{2}]^{1/2} \nonumber \]

El vector unitario en la dirección de\(\textbf{r}_{QP}\) es

\[\textbf{i}_{QP} = \frac{\textbf{r}_{QP}}{r_{QP}} \nonumber \]

Figura 2-14 La distancia vectorial r _QP entre dos puntos Q y P

b) Gradiente de la Distancia Recíproca,\(\nabla (1/r_{QP})\)

Tomando el gradiente del recíproco de (2) rendimientos

\[\nabla(\frac{1}{r_{QP}}) = \textbf{i}_{x} \frac{\partial}{\partial x} (\frac{1}{r_{QP}}) + \textbf{i}_{y} \frac{\partial}{\partial y}(\frac{1}{r_{QP}}) + \textbf{i}_{z} \frac{\partial}{\partial z} (\frac{1}{r_{QP}}) \\ = -\frac{1}{r^{3}_{QP}} [(x - x_{Q})\textbf{i}_{x} + (y-y_{Q})\textbf{i}_{y} + (z - z_{Q}) \textbf{i}_{z}] \\ = - \textbf{i}_{QP}/r^{2}_{QP} \nonumber \]

que es lo negativo del término espacialmente dependiente que integramos para encontrar el campo eléctrico en la Sección 2.3.2.

c) Laplaciano de la Distancia Recíproca

Otra identidad útil se obtiene tomando la divergencia del gradiente de la distancia recíproca. Esta operación se llama la Laplaciana de la distancia recíproca. Tomando la divergencia de (4) rendimientos

\[\nabla^{2} (\frac{1}{r_{QP}}) = \nabla \cdot [\nabla (\frac{1}{r_{QP}})] \\ = \nabla \cdot (\frac{-\textbf{i}_{QP}}{r^{2}_{QP}}) \\ = -\frac{\partial}{\partial x} (\frac{x-x_{Q}}{r^{3}_{QP}}) - \frac{\partial}{\partial y} (\frac{y-y_{Q}}{r^{3}_{QP}}) - \frac{\partial}{\partial z} (\frac{z - z_{Q}}{r^{3}_{QP}}) \\ = - \frac{3}{r^{3}_{QP}} + \frac{3}{r^{5}_{QP}} [(x-x_{Q})^{2} + (y - y_{Q})^{2} + (z-z_{2})^{2}] \nonumber \]

Usando (2) vemos que (5) reduce a

\[\nabla^{2} (\frac{1}{r_{QP}}) = \left \{ \begin{matrix} 0, & r_{QP} \neq 0 \\ \textrm{undefined} & r_{QP} = 0 \end{matrix} \right. \nonumber \]

Así, el Laplaciano de la distancia inversa es cero para todas las distancias distintas de cero pero no está definido cuando el punto de campo coincide con el punto de origen.

Ley de Gauss en forma integral

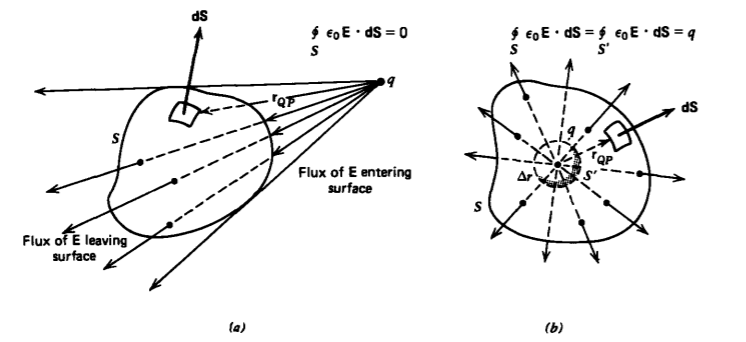
(a) Carga puntual dentro o fuera de un volumen cerrado Ahora considere los dos casos ilustrados en la Figura 2-15 donde un volumen cerrado de forma arbitraria V rodea una carga puntual q o está cerca de una carga puntual q fuera de la superficie S. Para cualquier caso el campo eléctrico emana radialmente de la carga puntual con la ley cuadrada inversa espacial. Deseamos calcular el flujo del campo eléctrico a través de la superficie S que rodea el volumen V:

\[\Phi = \oint_{S} \textbf{E} \cdot \textbf{dS} \\ = \oint_{S} \frac{q}{4 \pi \varepsilon_{0}r^{2}_{QP}} \textbf{i}_{QP} \cdot \textbf{dS} \\ = \oint_{S} \frac{-q}{4 \pi \varepsilon_{0}} \nabla (\frac{1}{r_{QP}}) \cdot \textbf{dS} \nonumber \]

Figura 2-15 (a) El flujo neto del campo eléctrico a través de una superficie cerrada S debido a una carga puntual exterior es cero porque tanto flujo ingresa al lado cercano de la superficie como sale en el lado lejano. b) Todo el flujo de campo eléctrico que emana de una carga puntual encerrada pasa por la superficie.

donde usamos (4). Ahora podemos usar el teorema de divergencia para convertir la integral de superficie en una integral de volumen:

\[\oint_{S} \textbf{E} \cdot \textbf{dS} = \frac{-q}{4 \pi \varepsilon_{0}} \nabla \cdot [ \nabla (\frac{1}{r_{QP}})] dV \nonumber \]

Cuando la carga puntual q está fuera de la superficie, cada punto del volumen tiene un valor distinto de cero de r _QP. Entonces, usando (6) con\(r_{QP} \neq 0\), vemos que el flujo neto de E a través de la superficie es cero.

Este resultado se puede entender examinando la Figura 2-15 a. El campo eléctrico que emana de q en esa parte de la superficie S más cercana a q tiene su componente normal dirigida opuestamente a dS dando una contribución negativa al flujo. Sin embargo, en el lado opuesto de S el campo eléctrico sale con su componente normal en la misma dirección que dS dando una contribución positiva al flujo. Hemos demostrado que estas contribuciones de flujo son iguales en magnitud pero opuestas en signo para que el flujo neto sea cero.

Como se ilustra en la Figura 2-15 b, suponiendo q es positivo, vemos que cuando S rodea la carga el campo eléctrico apunta hacia afuera con componente normal en la dirección de dS en todas partes sobre S de manera que el flujo debe ser positivo. Si q fueran negativos, E y dS estarían dirigidos opuestamente en todas partes para que el flujo también sea negativo. Para cualquier polaridad con q distinto de cero, el flujo no puede ser cero. Para evaluar el valor de este flujo nos damos cuenta de que (8) es cero en todas partes excepto donde r _QP =0 para que la superficie S en (8) se pueda reducir a una pequeña superficie esférica S' de radio infinitesimal\(\Delta r\) que rodea la carga puntual; el resto de el volumen tiene de\(\r_{QP} \neq 0\) manera que\(\nabla \cdot \nabla (1/r_{QP}) = 0\) En esta superficie incremental sabemos que el campo eléctrico es puramente radial en la misma dirección que d S' con el campo debido a una carga puntual:

\[\oint_{S} \textbf{E} \cdot \textbf{dS} = \oint_{S'} \textbf{E} \cdot \textbf{dS}' = \frac{q}{4 \pi \varepsilon_{0}(\Delta r)^{2}} 4 \pi (\Delta r)^{2} = \frac{q}{\varepsilon_{0}} \nonumber \]

Si tuviéramos muchas cargas puntuales dentro de la superficie S, cada carga q _i da lugar a un flujo de\(q_{i}/ \varepsilon_{0}\) manera que la ley de Gauss establece que el flujo neto\(\varepsilon_{0}\textbf{E}\) a través de una superficie cerrada es igual a la carga neta encerrada por la superficie:

\[\oint_{S} \varepsilon_{0} \textbf{E} \cdot \textbf{dS} = \sum_{\textrm{all } q_{i} \textrm{ inside } S} q_{i} \nonumber \]

Cualquier carga fuera de S no contribuye al flujo

(b) Distribuciones de Cargas

Para distribuciones continuas de carga, el lado derecho de (10) incluye la suma de todos los elementos de carga incrementales encerrados para que la carga total encerrada pueda ser una integral de línea, superficie y/o volumen además de la suma de cargas puntuales:

\[\oint_{S} \varepsilon_{0} \textbf{E} \cdot \textbf{dS} = \sum_{\textrm{all } q_{i} \textrm{ inside } S} q_{i} + \int_{\textrm{all } q \textrm{ inside} S} dq \\ = (\sum q_{i} + \int_{L} \lambda dl + \int_{S} \sigma d \textrm{S} + \int_{\textrm{V}} \rho d \textrm{V} \bigg|_{\textrm{all charge inside} S} \nonumber \]

Las cargas fuera del volumen no contribuyen al flujo total a través de la superficie circundante.

La ley de Gauss de (11) se puede utilizar con gran ventaja para simplificar los cálculos para aquellas cargas distribuidas con simetría espacial. El truco es encontrar una superficie S que tenga secciones tangentes al campo eléctrico para que el producto punto sea cero, o tenga superficies perpendiculares al campo eléctrico y sobre las cuales el campo sea constante para que el producto puntual y la integración se conviertan en multiplicaciones puras. Si se encuentra la superficie apropiada, la integral de la superficie se vuelve muy simple de evaluar.

La integral de superposición de Coulomb derivada en la Sección 2.3.2 se usa a menudo con distribuciones de carga simétricas para determinar si algún componente de campo es cero. Conocer la dirección del campo eléctrico suele sugerir la superficie gaussiana apropiada sobre la cual integrarse (11). Esta integración suele ser mucho más simple que usar la ley de Coulomb para cada elemento de carga

Simetría esférica

(a) Carga superficial

Una esfera de radio R tiene una distribución uniforme de carga superficial\(\sigma_{0}\) como en la Figura 2-16 a. Mida el ángulo\(\theta\) desde la línea que une cualquier punto P a una distancia radial r al centro de la esfera. Entonces, la distancia de P a cualquier elemento de carga superficial en la esfera es independiente del ángulo\(\phi\). Cada elemento de carga superficial diferencial en ángulo\(\theta\) aporta componentes de campo en las\(\theta\) direcciones radial y radial, pero los elementos de carga ubicados simétricamente en -\(\phi\) tienen componentes de igual magnitud de campo que se suman radialmente pero cancelan en la\(\theta\) dirección.

Al darse cuenta de la simetría de que el campo eléctrico es puramente radial y solo depende de r y no de\(\theta\) o\(\phi\), dibujamos esferas gaussianas de radio r como en la Figura 2-16b tanto dentro (r < R) como fuera (r > R) el esfera cargada. La esfera gaussiana en el interior no encierra carga mientras que la esfera exterior

Figura 2-16 Una esfera de radio R con carga superficial uniformemente distribuida\(\sigma_{0}\). a) Los elementos de carga ubicados simétricamente muestran que el campo eléctrico es puramente radial. (b) La ley de Gauss, aplicada a las superficies esféricas concéntricas dentro (r < R) y fuera (r > R) de la esfera cargada, muestra fácilmente que el campo eléctrico dentro de la esfera es cero y el exterior es el mismo que si toda la carga\(Q = 4 \pi R^{2} \sigma_{0}\) estuviera concentrada como punto de carga en el origen.

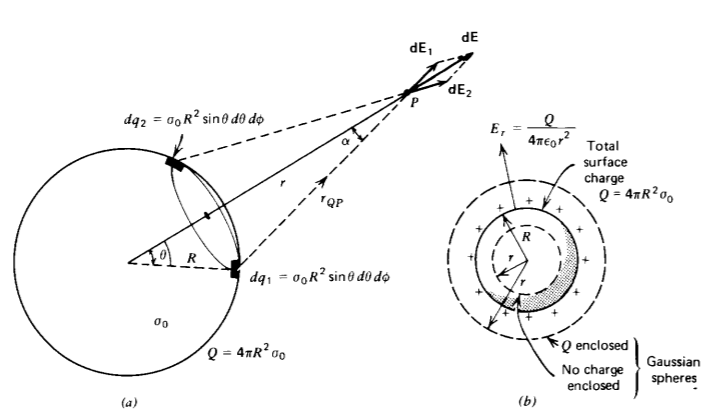
encierra todos los cargos\(Q = \sigma_{0} 4 \pi R^{2}\):

\[\oint_{S} \varepsilon_{0} \textbf{E} \cdot \textbf{dS} = \varepsilon_{0} E_{r} 4 \pi r^{2} = \left \{ \begin{matrix} \sigma_{0} 4 \pi R^{2} = Q, & r > R \\ 0, & r<R \end{matrix} \right. \nonumber \]

para que el campo eléctrico sea

\[E_{r} = \left \{ \begin{matrix} \frac{\sigma_{0}R^{2}}{\varepsilon_{0}r^{2}} = \frac{Q}{4 \pi \varepsilon_{0}r^{2}}, & r > R \\ 0, & r<R \end{matrix} \right. \nonumber \]

La integración en (12) equivale a solo una multiplicación de\(\varepsilon_{0}E_{r}\), y el área superficial de la esfera gaussiana porque en la esfera el campo eléctrico es constante y en la misma dirección que el ir normal. El campo eléctrico fuera de la esfera es el mismo que si toda la carga superficial estuviera concentrada como una carga puntual en el origen.

La solución de campo cero para r < R es lo que realmente demostró la ley de Coulomb. Después de todo, las pequeñas esferas de Coulomb no eran realmente cargas puntuales y sus medidas sí tenían pequeñas fuentes de errores. Quizás la fuerza eléctrica sólo varió inversamente con la distancia por alguna potencia cercana a dos\(r^{-2 + \delta}\),, donde\(\delta\) es muy pequeña. Sin embargo, solo la ley cuadrada inversa da un campo eléctrico cero dentro de una esfera uniformemente cargada en la superficie. Este resultado de campo cero es cierto para cualquier cuerpo conductor cerrado de forma arbitraria cargado en su superficie sin carga cerrada. Se realizaron mediciones extremadamente precisas dentro de tales cuerpos conductores cargados en superficie y el campo eléctrico siempre se encontró que era cero. Dicho cuerpo conductor cerrado se utiliza para apantallar de manera que un entorno de campo cero pueda aislarse y a menudo se llama jaula de Faraday, después de las mediciones de Faraday de subir realmente a un cuerpo conductor hueco cerrado cargado en su superficie para verificar los resultados de campo cero.

Para apreciar la facilidad de solución usando la ley de Gauss, rehagamos el problema usando la integral de superposición de la Sección 2.3.2. De la Figura 2-16a el componente radial incremental del campo eléctrico debido a un elemento de carga diferencial es

\[dE_{r} = \frac{\sigma_{0}R^{2} \sin \theta \: d \theta \: d \phi}{4 \pi \varepsilon_{0}r^{2}_{QP}} \cos \alpha \nonumber \]

De la ley de los cosenos se relacionan los ángulos y distancias como

\[r_{QP}^{2} = r^{2} + R^{2} - 2rR \: \cos \: \theta \\ R^{2} = r^{2} + r_{QP}^{2} - 2 r r_{QP} \cos \: \alpha \nonumber \]

por lo que\(\alpha\) se relaciona con\(\theta\) como

\[\cos \alpha = \frac{r - R \cos \theta}{[r^{2} + R^{2} - 2 r R \: \cos \theta]^{1/2}} \nonumber \]

Entonces la integral de superposición de la Sección 2.3.2 nos obliga a integrar (14) como

\[E_{r} = \int_{\theta = 0}^{\pi} \int_{\phi = 0}^{2 \pi} \frac{\sigma_{0}R^{2} \sin \: \theta (r-R \: \cos \: \theta) d \theta d \phi}{4 \pi \varepsilon_{0}[r^{2} + R^{2} - 2rR \: \cos \: \theta]^{3/2}} \nonumber \]

Después de realizar la fácil integración sobre\(\phi\) eso arroja el factor de\(2 \pi\), introducimos el cambio de variable:

\[u = r^{2} + R^{2} - 2 r R \: \cos \: \theta \\ du = 2 r R \: \sin \theta \: d \theta \nonumber \]

lo que nos permite reescribir el campo eléctrico integral como

\[E_{r} = \int_{u = (r-R)^{2}}^{(r + R)^{2}} \frac{\sigma_{0}R[u + r^{2} - R^{2}] du}{8 \varepsilon_{0}r^{2}u^{3/2}} \\ = \frac{\sigma_{0}R}{4 \varepsilon_{0} r^{2}} (u^{1/2} - \frac{(r^{2}-R^{2})}{u^{1/2}} ) \bigg|_{(r-R)^{2}}^{(r + R)^{2}} \\ = \frac{\sigma_{0}R}{4 \varepsilon_{0}r^{2}}[(r + R) - \vert r - R \vert - (r^{2} - R^{2}) (\frac{1}{r + R} - \frac{1}{\vert r - R \vert})] \nonumber \]

donde hay que tener mucho cuidado de tomar la raíz cuadrada positiva en la evaluación del límite inferior de la integral para r < R. Evaluar (19) para r mayor y menor que R nos da (13), pero con mucho más esfuerzo.

b) Distribución de carga por volumen

Si la esfera está uniformemente cargada con densidad\(\rho_{0}\), entonces la superficie gaussiana en la Figura 2-17 a para r > R aún encierra la carga total\(Q = \frac{4}{3} \pi R^{3} \rho_{0}\). Sin embargo, ahora la superficie gaussiana más pequeña con r < R encierra una fracción de la carga total:

\[\oint_{S} \varepsilon_{0} \textbf{E} \cdot \textbf{dS} = \varepsilon_{0}E_{r} 4 \pi r^{2} = \left \{ \begin{matrix} \rho_{0} \frac{4}{3} \pi r^{3} = Q(r/R)^{3}, & r<R \\ \rho_{0}\frac{4}{3} \pi R^{3} = Q, & r>R \end{matrix} \right. \nonumber \]

Figura 2-17 (a) Las esferas gaussianas para una esfera cargada uniformemente muestran que el campo eléctrico fuera de la esfera vuelve a ser el mismo que si toda la carga\(Q = \frac{4}{3} \pi R^{3} \rho_{0}\) estuviera concentrada como una carga puntual a r =0. b) La solución también se obtiene sumando las contribuciones de las conchas esféricas incrementales de carga superficial.

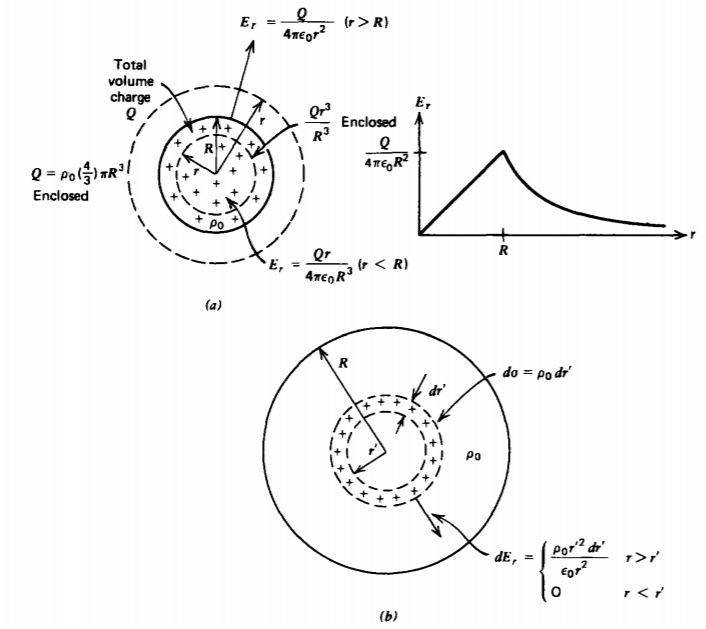
para que el campo eléctrico sea

\[E_{r} = \left \{ \begin{matrix} \frac{\rho_{0}r}{3 \varepsilon_{0}} = \frac{Qr}{4 \pi \varepsilon_{0} R^{3}}, & r < R \\ \frac{\rho_{0}R^{3}}{3 \varepsilon_{0}r^{2}} = \frac{Q}{4 \pi \varepsilon_{0}r^{2}}, & r > R \end{matrix} \right. \nonumber \]

Este resultado también podría haberse obtenido utilizando los resultados de (13) rompiendo el volumen esférico en conchas incrementales de radio r ', espesor dr', portando carga superficial diferencial\(d \sigma = \rho_{0} dr'\) como en la Figura 2-17 b. Entonces la contribución al campo es cero dentro de cada shell pero distinta de cero afuera:

\[dE_{r} = \left \{ \begin{matrix} 0, & r<r' \\ \frac{\rho_{0}r'^{2} dr'}{\varepsilon_{0}r^{2}}, & r>r' \end{matrix} \right. \nonumber \]

El campo total fuera de la esfera se debe a todos los proyectiles diferenciales, mientras que el campo interior se debe únicamente a los proyectiles cerrados:

\[E_{r} = \left \{ \begin{matrix} \int_{0}^{r} \frac{r'^{2}\rho_{0}dr'}{\varepsilon_{0}r^{2}} = \frac{\rho_{0}r}{3 \varepsilon_{0}} = \frac{Qr}{4 \pi \varepsilon_{0}R^{3}}, & r<R \\ \int_{0}^{R} \frac{r'^{2} \rho_{0}dr'}{\varepsilon_{0}r^{2}} = \frac{\rho_{0}R^{3}}{3 \varepsilon_{0}r^{2}} = \frac{Q}{4 \pi \varepsilon_{0}r^{2}}, & r>R \end{matrix} \right. \nonumber \]

que concuerda con (21)

Simetría cilíndrica

(a) Cilindro hueco de carga superficial

Un cilindro infinitamente largo de radio a tiene una distribución uniforme de la carga superficial\(\sigma_{0}\), como se muestra en la Figura 2-18 a. El ángulo\(\phi\) se mide desde la línea que une el punto de campo P hasta el centro del cilindro. Cada elemento\(d \lambda = \sigma_{0}a \: d \phi\) de carga de línea incremental contribuye al campo eléctrico en P como lo da la solución para una carga de línea infinitamente larga en la Sección 2.3.3. Sin embargo, el elemento ubicado simétricamente\(-\phi\) da lugar a componentes de campo de igual magnitud que se suman radialmente según se miden desde el centro del cilindro pero cancelan en la\(\phi\) dirección

Debido a la simetría, el campo eléctrico es puramente radial por lo que utilizamos la ley de Gauss con un cilindro concéntrico de radio r y altura L, como en la Figura 2-18 b donde L es arbitrario. No hay contribución a la ley de Gauss desde las superficies superior e inferior porque el campo eléctrico es puramente tangencial. A lo largo de la pared cilíndrica en el radio r, el campo eléctrico es constante y

Figura 2-18 (a) Los elementos de carga de línea ubicados simétricamente en un cilindro con carga superficial uniformemente distribuida muestran que el campo eléctrico es puramente radial. b) La ley de Gauss aplicada a superficies cilíndricas concéntricas muestra que el campo dentro del cilindro con carga superficial es cero mientras que fuera es el mismo que si toda la carga por unidad de longitud\(\sigma_{0} 2 \pi a\) estuviera concentrada en el origen como carga de línea. (c) Además de usar las superficies de (b) con la ley de Gauss para un cilindro de carga volumétrica, también podemos sumar las contribuciones de cilindros huecos incrementales de carga superficial.

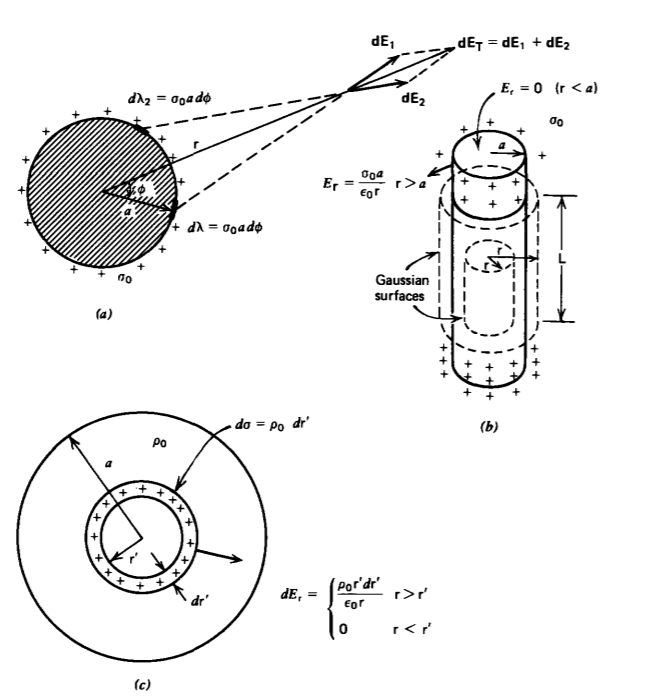
puramente normal para que la ley de Gauss simplemente rinda

\[\oint_{S} \varepsilon_{0} \textbf{E} \cdot \textbf{dS} = \varepsilon_{0} L_{\textrm{r}} 2 \pi \textrm{r} L = \left \{ \begin{matrix} \sigma_{0} 2 \pi aL, & \textrm{r} > a \\ 0 & \textrm{r} < a \end{matrix} \right. \nonumber \]

donde para r< a se encierra toda la carga dentro de una altura L. El campo eléctrico fuera del cilindro es entonces el mismo que si toda la carga por unidad de longitud\(\lambda = \sigma_{0} 2 \pi a\) estuviera concentrada a lo largo del eje del cilindro:

\[E_{r} = \left \{ \begin{matrix} \frac{\sigma_{0}a}{\varepsilon_{0} \textrm{r}} = \frac{\lambda}{2 \pi \varepsilon_{0} \textrm{r}} & \textrm{r} > a \\ 0, & \textrm{r} < a \end{matrix} \right. \nonumber \]

Anote en (24) que la altura arbitraria L canceló.

(b) Cilindro de carga volumétrica

Si el cilindro está cargado uniformemente con densidad\(\rho_{0}\), ambas superficies gaussianas en la Figura 2-18 b encierran carga

\[\oint_{S} \varepsilon_{0} \textbf{E} \cdot \textbf{dS} = \varepsilon_{0} E_{\textrm{r}} 2 \pi \textrm{r} L= \left \{ \begin{matrix{ \rho_{0} \pi a^{2} L, & \textrm{r}>a \\ \rho_{0} \pi \textrm{r}^{2}L, & \textrm{r} < a \end{matrix} \right. \nonumber \]

para que el campo eléctrico sea

\[E_{\textrm{r}} = \left \{ \begin{matrix} \frac{\rho_{0}a^{2}}{2 \varepsilon_{0} \textrm{r}} = \frac{\lambda}{2 \pi \varepsilon_{0} \textrm{r}}, & \textrm{r} > a \\ \frac{\rho_{0} \textrm{r}}{2 \varepsilon_{0}} = \frac{\lambda \textrm{r}}{2 \pi \varepsilon_{0} a^{2}} & \textrm{r} < a \end{matrix} \right. \nonumber \]

donde\(\lambda = \rho_{0} \pi a^{2}\) es la carga total por unidad de longitud en el cilindro.

Por supuesto, este resultado también podría haberse obtenido integrando (25) para todas las carcasas cilíndricas diferenciales de radio r' con espesor d r' llevando carga superficial incremental\(d \sigma = \rho_{0} d \textrm{r}'\), como en la Figura 2-18 c

\[E_{\textrm{r}} = \left \{ \begin{matrix} \int_{0}^{a} \frac{\rho_{0}\textrm{r}'}{\varepsilon_{0}\textrm{r}} d \textrm{r}' = \frac{\rho_{0}}{2 \varepsilon_{0} \textrm{r}} = \frac{\lambda}{2 \pi \varepsilon_{0} \textrm{r}}, & \textrm{r} > a \\ \int_{0}^{\textrm{r}} \frac{\rho_{0} \textrm{r}'}{\varepsilon_{0} \textrm{r}} d \textrm{r}' = \frac{\rho_{0} \textrm{r}}{2 \varepsilon_{0}} = \frac{\lambda \textrm{r}}{2 \pi \varepsilon_{0} a^{2}}, & \textrm{r} < a \end{matrix} \right. \nonumber \]

La ley de Gauss y el teorema de la divergencia

Si una distribución de volumen de carga\(\rho\) está completamente rodeada por una superficie Gaussiana cerrada S, la ley de Gauss de (11) es

\[\oint_{S} \varepsilon_{0} \textbf{E} \cdot \textbf{dS} = \int_{V} \rho d V \nonumber \]

El lado izquierdo de (29) se puede cambiar a una integral de volumen usando el teorema de divergencia:

\[\oint_{S} \varepsilon_{0} \textbf{E} \cdot \textbf{dS} = \int_{V} \nabla \cdot (\varepsilon_{0} \textbf{E}) dV = \int_{V} \rho d V \nonumber \]

Dado que (30) debe mantenerse para cualquier volumen, los integros de volumen en (30) deben ser iguales, dando la forma puntual de la ley de Gauss:

\ [\ nabla\ cdot (\ varepsilon_ {0}\ textbf {E}) =\ rho\)

Dado que la permitividad del espacio libre\(\varepsilon_{0}\) es una constante, puede moverse libremente fuera del operador de divergencia.

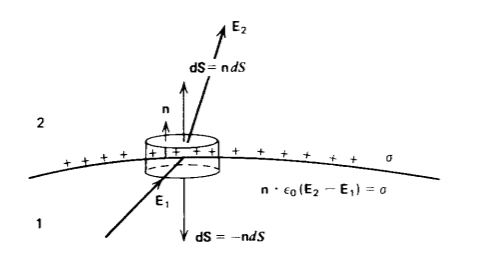
Discontinuidad del campo eléctrico a través de una lámina de carga superficial

En la Sección 2.3.4 a encontramos que el campo eléctrico cambia de dirección discontinuamente a cada lado de una lámina recta de carga superficial. Podemos ser más generales aplicando la forma integral superficial de la ley de Gauss en (30) a la superficie de la caja de bolitas de tamaño diferencial mostrada en la Figura 2-19 rodeando un área pequeña dS de carga superficial

\[\oint_{S} \varepsilon_{0} \textbf{E} \cdot \textbf{dS} = \int_{S} \sigma d S \Rightarrow \varepsilon_{0} (E_{2n} - E_{1n}) dS = \sigma dS \nonumber \]

donde E _2n y E _1n son los componentes perpendiculares del campo eléctrico en cada lado de la interfaz. Solo las superficies superior e inferior de la caja de bolitas contribuyen en (32) porque se supone que la carga superficial tiene espesor cero para que la superficie cilíndrica corta tenga área cero. Así vemos que la densidad de carga superficial es proporcional a la discontinuidad en el componente normal del campo eléctrico a través de la lámina:

\[\varepsilon_{0}(E_{2n} - E_{1n}) = \sigma \Rightarrow \textbf{n} \cdot \varepsilon_{0}(\textbf{E}_{2} - \textbf{E}_{1}) = \sigma \nonumber \]

donde n es perpendicular a la interfaz dirigida de la región 1 a la región 2.

Figura 2-19 La ley de Gauss aplicada a una superficie de caja de bolitas de tamaño diferencial que encierra alguna carga superficial muestra que el componente normal de\(\varepsilon_{0}\textbf{E}\) es discontinuo en la densidad de carga superficial.