2.8: Problemas
- Page ID
- 86820
Sección 2.1
El experimento de “cubeta de hielo” de Faraday se repite con la siguiente secuencia de pasos:
(i) Una bola con carga total\(\mathcal{Q}\) se introduce dentro de una cubeta de hielo metálica aislada sin tocarla.
(ii) El exterior del balde se conecta momentáneamente a tierra y luego se desconecta para que una vez más el balde quede aislado.
(iii) Sin tocar el balde, se retira la bola cargada.
(a) Esbozar la distribución de carga en el interior y el exterior del cubo durante cada escalón.
(b) Cuál es la carga neta sobre el balde después de retirar la bola cargada
Una esfera que inicialmente lleva una carga total\(\mathcal{Q}\) se pone en contacto momentáneo con una esfera idéntica no cargada.
a) ¿Cuánta carga hay en cada esfera?
b) Este proceso se repite para esferas\(N\) idénticas inicialmente sin carga. Cuanta carga hay en cada una de las esferas incluyendo la esfera cargada original
c) ¿Cuál es la carga total en el sistema después de los\(N\) contactos?
Sección 2.2
La carga de un electrón fue medida por primera vez por Robert A. Millikan en 1909 midiendo el campo eléctrico necesario para levitar una pequeña caída de petróleo cargada contra su peso. Las gotitas de aceite se pulverizaron y se cargaron por electrificación por fricción
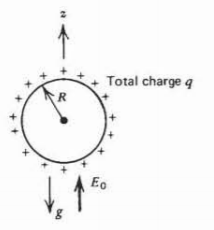
Una gotita esférica de radio \(R\)y densidad de masa efectiva\(\rho_{m}\) lleva una carga total\(q\) en un campo de gravedad\(g\). ¿Qué campo eléctrico\(E_{0}\textrm{i}_{z}\) suspenderá la gotita cargada? Millikan encontró por este método que todas las gotitas portaban múltiplos enteros de carga negativa\(e=-1.6\times10^{19}\,\textrm{coul}\).
Dos pequeñas bolas conductoras, cada una de masa\(m\), están al final de cuerdas aislantes de longitud \(l\)unidas en un punto. Se colocan cargas en las bolas para que estén a una distancia de\(d\) distancia. Se\(\mathcal{Q}_{1}\) coloca una carga sobre la pelota\(1\). ¿Cuál es la carga\(\mathcal{Q}_{2}\) en la pelota\(2\)?
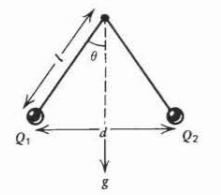
Una carga puntual\(-\mathcal{Q}_{1}\) de masa\(m\) viaja en una órbita circular de radio\(R\) alrededor de una carga de signo opuesto\(\mathcal{Q}_{2}\).
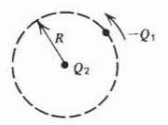
a) ¿Cuál es la velocidad angular de equilibrio de la carga\(-\mathcal{Q}_{1}\)?
(b) T su problema describe el modelo de un solo electrón de Bohr del átomo si la carga\(-\mathcal{Q}_{1}\) es la de un electrón y\(\mathcal{Q}_{2}=Ze\) es la carga nuclear, donde\(Z\) está el número de protones. Según los postulados de la mecánica cuántica se debe cuantificar el momento angular\(L\) del electrón,
\(L = mvR = nh/2\pi\),\(n = 1, 2, 3, ..\)
donde\(h=6.63\times 10^{-34}\,\textrm{joule-sec}\) está la constante de Planck. ¿Cuáles son los valores permitidos\(R\)?
(c) Para el átomo de hidrógeno\(\left ( Z=1 \right )\) ¿cuál es el radio de la órbita más pequeña permitida y cuál es la velocidad orbital del electrón?
Un electroscopio mide la carga por la deflexión angular de dos bolas conductoras idénticas suspendidas por una cuerda aislante esencialmente ingrávida de longitud\(l\). Cada bola tiene masa\(M\) en el campo de gravedad \(g\)y cuando está cargada puede considerarse una carga puntual.
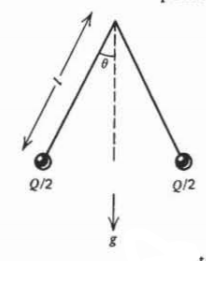
\(\mathcal{Q}\)Se deposita una carga total sobre las dos bolas del electroscopio. El ángulo\(\theta\) desde lo normal obedece a una relación de la para
\[\tan \theta \sin^{2} \theta = \textrm{const} \nonumber \]
¿Cuál es la constante?
Dos cargas puntuales\(q_{1}\) y \(q_{2}\)en vacío con respectivas masas\(m_{1}\) y se\(m_{2}\) atraen (o repelen) entre sí a través de la fuerza del culombo.
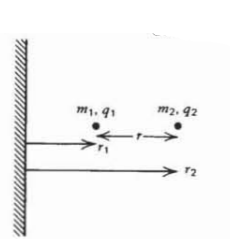
(a) Escribir una única ecuación diferencial para la distancia entre las cargas\(r = r_{2} - r_{1}\). ¿Cuál es la masa efectiva de los cargos? (Pista: Escribe la ley de Newton para cada carga y toma una diferencia ponderada en masa).
b) Si las dos cargas son liberadas del reposo \(t=0\)cuando están a una\(r_{0}\) distancia entre sí, ¿cuál es su velocidad\(v = dr/dt\) relativa en función \(r\)? Insinuación:
\[\frac{dv}{dt} = \frac{dv}{dr} \frac{dr}{dt} = v \frac{dv}{dr} = \frac{d}{dr} (\frac{1}{2} v^{2}) \nonumber \]
c) ¿Cuál es su posición en función del tiempo? Consideremos por separado los casos en que las cargas tengan la misma polaridad u opuesta. Insinuación:
Let\(u = \sqrt{r}\)
\(\int \frac{u^{2}du}{\sqrt{a^{2} - u^{2}}} = -\frac{u}{2} \sqrt{a^{2} - u^{2}} + \frac{a^{2}}{2} \sin^{-1} \frac{u}{a}\)
\(\int \frac{u^{2}du}{\sqrt{u^{2}-a^{2}}} = \frac{u}{2} \sqrt{u^{2} - a^{2}} + \frac{a^{2}}{2} \ln (u + \sqrt{u^{2} - a^{2}})\)
d) Si las cargas son de polaridad opuesta, ¿a qué hora chocarán? (Pista: Si obtiene un valor negativo del tiempo, verifique sus signos de raíces cuadradas en (b).)
e) Si las cargas se sacan del vacío y se colocan en un medio viscoso, la velocidad y no la aceleración es proporcional a la fuerza
\(\beta_{1} \textbf{v}_{1} = \textbf{f}_{1},\)\(\beta_{2} \textbf{v}_{2} = \textbf{f}_{2}\)
donde\(\beta_{1}\) y\(\beta_{2}\) son los coeficientes de fricción para cada carga. Repita las partes (a) - (d) para este movimiento viscoso dominado
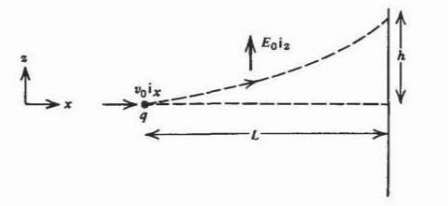
Una carga\(q\) de masa\(m\) con velocidad inicial\(\textbf{v} = v_{0}\textbf{i}_{x}\) se\(x=0\) inyecta en una región de campo eléctrico uniforme\(\textbf{E} = \textbf{E}_{0}\textbf{i}_{z}\). Se coloca una pantalla en la posición\(x=L\). ¿A qué altura\(h\) llega la carga a la pantalla? Negligencia por gravedad
Un péndulo con una cuerda de longitud ingrávida\(l\) tiene en su extremo una pequeña esfera con carga\(q\) y masa\(m\). A distancia\(D\)
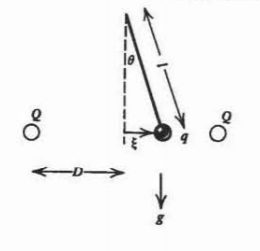
a ambos lados de la masa del péndulo hay dos esferas fijas cada una con una carga\(\mathcal{Q}\). Las tres esferas son de tamaño suficientemente pequeño para que puedan considerarse como cargas puntuales y masas.
(a) Suponiendo que el desplazamiento\(\xi\) del péndulo sea pequeño\(\xi <<D\)), muestran que la ley de Newton puede escribirse aproximadamente como
\(\frac{d^{2} \xi}{dt^{2}} + \omega_{0}^{2} \xi = 0\)
¿Qué es\(\omega^{2}_{0}\)? Insinuación:
\(\sin \theta \approx \frac{\xi}{l'} \: \: \frac{1}{(D \pm \xi)^{2}} \approx \frac{1}{D^{2}} \mp \frac{2 \xi}{D^{3}}\)
(b) En\(t=0\) el péndulo se libera del reposo con\(\xi = \xi_{0}\). ¿Cuál es el posterior movimiento del péndulo?
c) ¿Para qué valores de la moción no\(q\mathcal{Q}\) está delimitada con el tiempo?
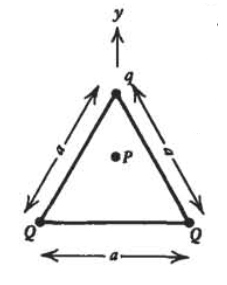
Carga\(\mathcal{Q}\),\(\mathcal{Q}\), y\(q\) se encuentran en las esquinas de un triángulo equilátero con lados de longitud\(a\).
a) ¿Cuál es la fuerza sobre la carga\(q\)?
b) ¿Qué debe\(q\) ser para\(\textbf{E}\) que sea cero a la mitad de la altitud a\(P\)?
Encuentra el campo eléctrico a lo largo del\(z\) eje debido a cuatro cargas puntuales de igual magnitud\(q\) colocadas en los vértices de un cuadrado con lados de longitud\(a\) en el\(xy\) plano centrado en el origen
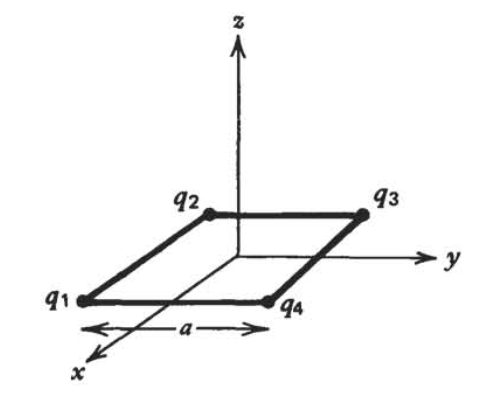
cuando:
a) las cargas tengan la misma polaridad,\(q_{1}=q_{2}=q_{3}=q_{4}\equiv =q\);
b) las cargas alternas en polaridad\(q_{1}=q_{3}\equiv q,\,q_{2}=q_{4}\equiv -q\);
(c) los cargos son\(q_{1}=q_{2}\equiv q,\,q_{3}=q_{4}\equiv -q\).
Sección 2.3
Encuentra el cargo total en cada una de las siguientes distribuciones donde\(a\) es un parámetro constante:
(a) Una carga de línea infinitamente larga con densidad
\(\lambda (z) = \lambda_{0} e^{- \vert z \vert / a}\)
b) Una carga volumétrica esféricamente simétrica distribuida por todo el espacio
\(\rho (r) = \frac{\rho_{0}}{[1 + r/a]^{4}}\)
(Pista: Vamos\(u = 1 + r/a\).)
c) Una hoja infinita de carga superficial con densidad
\(\sigma(x, y) = \frac{\sigma_{0} e^{- \vert x \vert a}}{[1 _ (y/b)^{2}]}\)
Una carga puntual\(q\) con masa\(M\) en un campo de gravedad\(g\) se libera del reposo a una distancia\(x_0\) por encima de una lámina de carga superficial con densidad uniforme\(\sigma_{0}\).
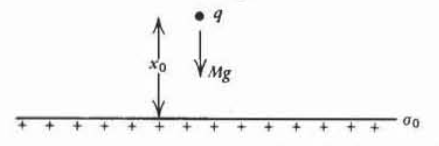
a) ¿Cuál es la posición de la carga en función del tiempo?
b) ¿Por qué valor\(\sigma_{0}\) se mantendrá estacionaria la carga?
c) Si\(\sigma_{0}\) es menor que el valor de (b), ¿en qué momento y con qué velocidad llegará la carga a la hoja?
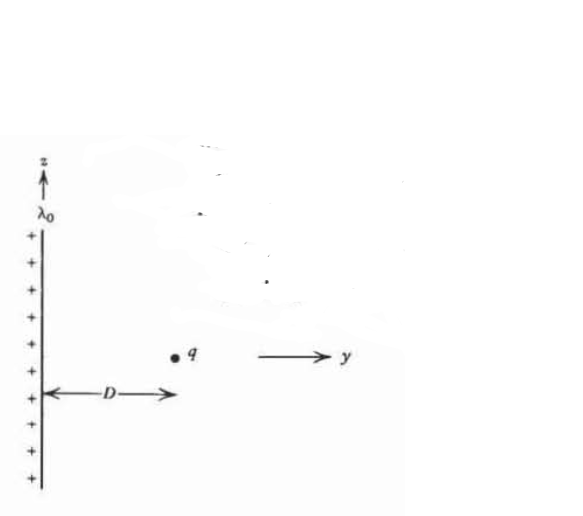
Una carga puntual\(q\) a\(z=0\) es una\(D\) distancia de una carga de línea infinitamente larga con densidad uniforme\(\lambda_{0}\).
a) ¿Cuál es la fuerza sobre la carga puntual\(q\)?
b) ¿Cuál es el cargo de fuerza en la línea?
(c) Repetir (a) y (b) si el cargo de línea tiene una distribución
\(\lambda (z) = \frac{\lambda_{0} \vert z \vert}{a}\)
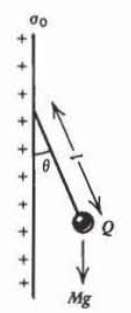
Una pequeña esfera de masa\(M\) en un campo de gravedad\(g\) que lleva una carga\(\mathcal{Q}\) está conectada por una cuerda sin masa a una lámina de carga superficial de la misma polaridad con densidad\(\sigma_{0}\). ¿Cuál es el ángulo\(\theta\) entre la hoja y la carga?
Una carga de línea\(\lambda\) a lo largo del\(z\) eje se extiende a lo largo del intervalo\(-L \leq z \leq L\).
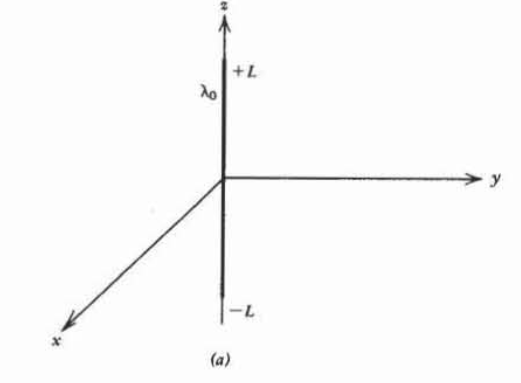
(a) Encontrar el campo eléctrico en el\(z=0\) avión.
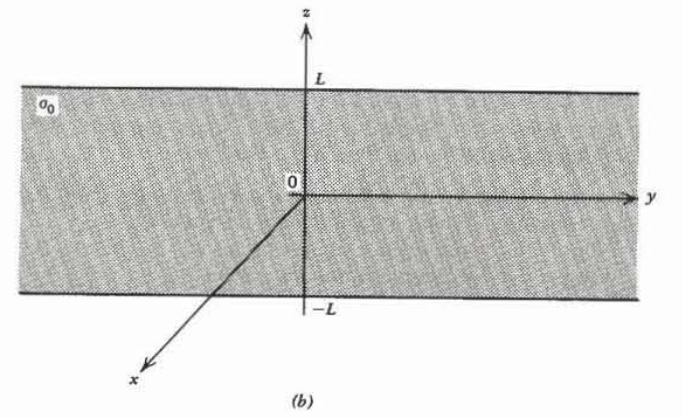
(b) Utilizando los resultados de (a) encontrar el campo eléctrico en el\(z=0\) plano debido a una franja infinita (\(- \infty \leq y \leq \infty\)) de altura\(2L\) con densidad de carga quirúrgica\(\sigma_{0}\). Consulta tus resultados con el texto para\(L \rightarrow \infty\). Insinuación: Let\(u = x^{2} + y^{2}\)
\(\int \frac{du}{u \sqrt{u - x^{2}} \sqrt{L^{2} + u}} = \frac{1}{Lx} \sin^{-1} (\frac{(L^{2} - x^{2}) u - 2L^{2}x^{2}}{u(L^{2} + x^{2})})\)
Un semi-cilindro hueco infinitamente largo de radio\(R\) lleva una distribución uniforme de la carga superficial\(\sigma_{0}\).
a) ¿Cuál es el campo eléctrico a lo largo del eje del cilindro?
(b) Utilizar los resultados de (a) para encontrar el campo eléctrico a lo largo del eje debido a un semicilindrico de carga volumétrica\(\rho_{0}\)
(c) Repita (a) y (b) para encontrar el campo eléctrico en el centro de un hemisferio uniformemente cargado de superficie o volumen.
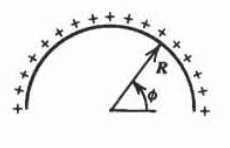
(a) Encontrar el campo eléctrico a lo largo del\(z\) eje de un bucle circular centrado en el\(xy\) plano de radio a que lleva una carga de línea uniforme\(\lambda_{0}\) para y > 0 y\(- \lambda_{0}\) para\(y<0\).
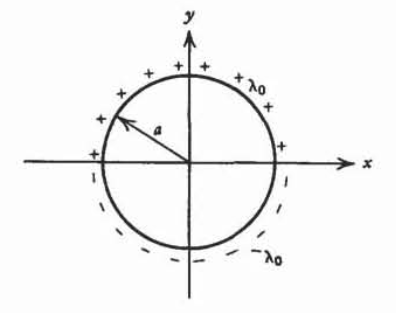
(b) Utilizar los resultados de (a) para encontrar el campo eléctrico a lo largo del eje z de un disco circular de radio a que lleve una carga superficial uniforme\(\sigma_{0}\) para\(y>0\) y\(-\sigma_{0}\) para\(y<0\).
(a) Encontrar el campo eléctrico a lo largo del\(z\) eje debido a un bucle cuadrado con lados de longitud\(a\) centrados alrededor del\(z\) eje en el\(xy\) plano que lleva una carga de línea uniforme\(\lambda\). ¿Para qué debería enfocarse su resultado\(z\gg a\)?
(b) Utilizar los resultados de (a) para encontrar el campo eléctrico a lo largo del\(z\) eje debido a un cuadrado de carga superficial uniforme\(\sigma_{0}\). Qué
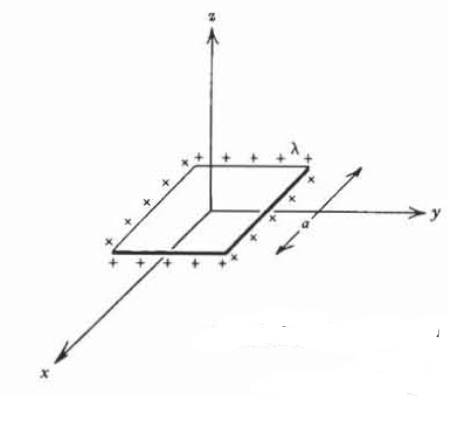
debe su enfoque de resultado como\(a \rightarrow \infty\)? Insinuación: Let
\(u = z^{2} + \frac{x^{2}}{4}, \: \int \frac{du}{u \sqrt{2u - z^{2}}} = \frac{2}{\vert z \vert} \tan^{-1} \sqrt{\frac{2u-z^{2}}{z^{2}}}\)
Un bucle circular de radio\(a\) en el\(xy\) plano tiene una distribución uniforme de carga de línea\(\lambda_{0}\) para\(y>0\) y\(-\lambda_{0}\) para\(y<0\).
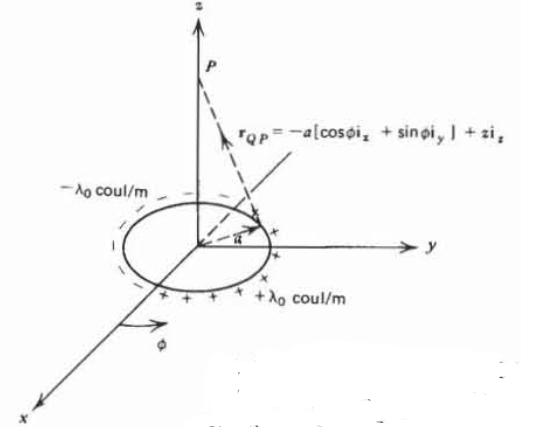
a) ¿Cuál es el campo eléctrico a lo largo del\(z\) eje?
b) Utilizar los resultados de (a) para encontrar el campo eléctrico a lo largo del\(z\) eje debido a un disco cargado en superficie, cuya densidad es\(\sigma_{0}\) para\(y>0\) y\(-\sigma_{0}\) para\(y<0\). Insinuación:
\(\int \frac{\textrm{r}^{2} d \textrm{r}}{(\textrm{r}^{2} + z^{2})^{3/2}} = - \frac{\textrm{r}}{\sqrt{\textrm{r}^{2} + z^{2}}} + \ln (\textrm{r} + \sqrt{\textrm{r}^{2} + z^{2}})\)
(c) Repita (a) si el cargo de línea tiene distribución\(\lambda = \lambda_{0} \sin \phi\).
(d) Repita (b) si la carga superficial tiene distribución\(\sigma = \sigma_{0} \sin \phi\).
Una carga de línea infinitamente larga con densidad\(\lambda_{0}\) se dobla por la mitad con ambas mitades unidas por un semicírculo de radio\(a\). Cuál es el campo eléctrico a lo largo del\(z\) eje que pasa por el centro
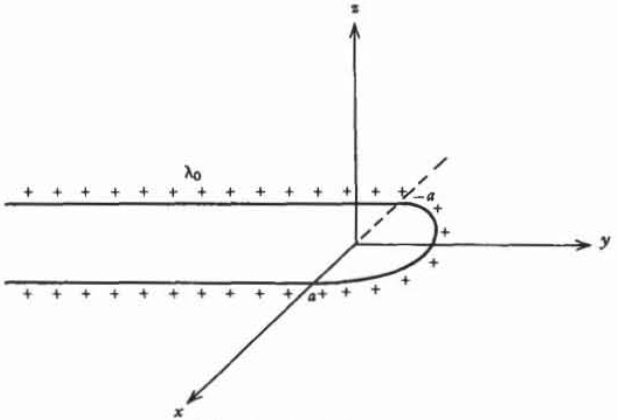
del círculo. Insinuación:
\(\displaystyle \int \frac{x dx}{[x^{2} + a^{2}]^{3/2}} = \frac{-1}{[x^{2} + a^{2}]^{1/2}} \\ \displaystyle \int \frac{dx}{[x^{2} + a^{2}]^{3/2}} = \frac{x}{a^{2} [x^{2} + a^{2}]^{1/2}} \\ \textbf{i}_{\textrm{r}} = \cos \phi \textbf{i}_{x} + \sin \phi \textbf{i}_{y}\)
Sección 2.4
Encuentre la carga total incluida dentro de cada uno de los siguientes volúmenes para los campos eléctricos dados:
a)\(\textbf{E} = Ar^{2} \textbf{i}_{r}\) para una esfera de radio\(R\);
b)\(\textbf{E} = A \textrm{r} \textbf{i}_{r}\) para un cilindro de radio a y longitud\(L\);
(c)\(\textbf{E} = A(x \textbf{i}_{x} + y \textbf{i}_{y})\) para un cubo con lados de una longitud\(a\) que tenga una esquina en el origen.
Encuentre el campo eléctrico en todas partes para las siguientes distribuciones de carga de volumen plano:
(a)\(\rho (x) = \rho_{0} e^{- \vert x \vert /a}, \: \: \: -\infty \leq x \leq \infty\)
b)\(\rho(x) = \left \{ \begin{matrix} - \rho_{0}, & -b \leq x \leq -a \\ \rho_{0}, & a \leq x \leq b \end{matrix} \right.\)
c)\(\rho (x) = \frac{\rho_{0}x}{d}, \: \: \: -d \leq x \leq d \)
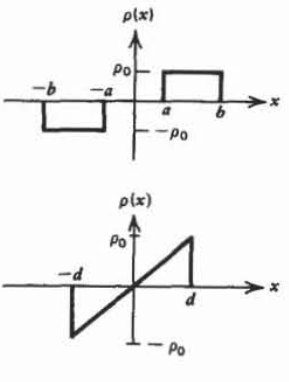
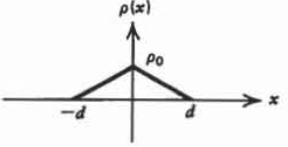
(d)\(\rho(x) = \left \{ \begin{matrix} \rho_{0}(1 + x/d), & -d \leq x \leq 0 \\ \rho_{0}(1-x/d), & 0 \leq x \leq d \end{matrix} \right.\)
Encuentre el campo eléctrico en todas partes para las siguientes distribuciones de carga de volumen esféricamente simétricas:
(a)\(\rho(r) = \rho_{0}e^{-r/a}, \: 0 \leq r \leq \infty\)
(Pista:\(\int r^{2} e^{-r/a} dr = -a e^{-e/a}[r^{2} + 2a^{2}(r/a + 1)].\))
b)\(rho (r) = \left \{ \begin{matrix} \rho_{1}, & 0 \leq r < R_{1} \\ \rho_{2}, & R_{1} < r < R_{2} \end{matrix} \right. \)
c)\(\rho(r) = \rho_{0}r/R, \quad 0 < r < R\)
Encuentre el campo eléctrico en todas partes para las siguientes distribuciones de carga volumétricas cilíndricamente simétricas:
(a)\(\rho(\textrm{r}) = \rho_{0}e^{-\textrm{r}/a}, \: 0 < \textrm{r} < \infty\)
[Pista:\(\displaystyle \int \textrm{r} = \rho_{0} e^{-\textrm{r}/a} , \: 0 < \textrm{r} < \infty\)
b)\(\rho(\textrm{r}) = \left \{ \begin{matrix} \rho_{1}, & 0 < \textrm{r} < a \\ \rho_{2}, & a < \textrm{r} < b \end{matrix} \right.\)
c)\(\rho(\textrm{r}) = \rho_{0} \textrm{r}/a, \: 0 < \textrm{r} < a\)
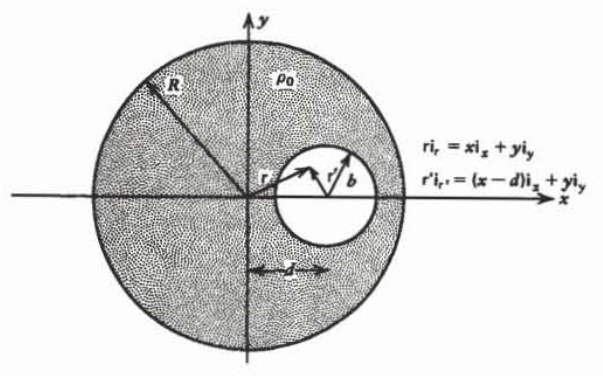
Un cilindro infinitamente largo de radio\(R\) con densidad de carga volumétrica uniforme\(\rho_{0}\) tiene un orificio de radio fuera del eje\(b\) con centro a una\(d\) distancia del centro del cilindro.
¿Cuál es el campo eléctrico dentro del agujero? (Pista: Reemplazar el agujero por la superposición de distribuciones de carga volumétrica de densidad\(\rho_{0}\)\(-\rho_{0}\) y utilizar los resultados de (27). Convierta las coordenadas cilíndricas a coordenadas cartesianas para facilitar la adición de vectores.)
Sección 2.5
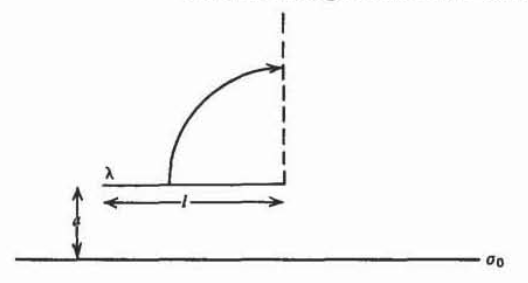
Una carga\(\lambda\) de línea de longitud\(l\) se encuentra paralela a una hoja infinita de carga superficial\(\sigma_{0}\). ¿Cuánto trabajo se requiere para rotar la carga de línea para que sea vertical?
Se\(m\) inyecta una carga puntual\(q\) de masa al infinito con velocidad inicial\(v_{0}\textbf{i}_{x}\) hacia el centro de una esfera de radio uniformemente cargada\(R\). La carga total sobre la esfera\(\mathcal{Q}\) es el mismo signo que\(q\).
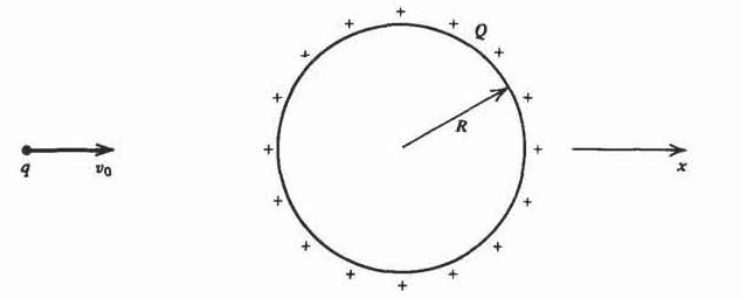
a) ¿Cuál es la velocidad inicial mínima necesaria para que la carga puntual colisione con la esfera?
b) Si la velocidad inicial es la mitad del resultado de la letra a), ¿qué tan cerca llega la carga a la esfera?
Encuentre las distribuciones de carga de campo eléctrico y volumen para las siguientes distribuciones potenciales:
(a)\(V = Ax^{2}\)
b)\(V = Axyz\)
c)\(V = A\textrm{r}^{2} \sin \phi + B \textrm{r}z\)
(d)\(V = Ar^{2} \sin \theta \cos \phi\)
¿Cuál de los siguientes vectores puede ser un campo eléctrico? Si es así, ¿cuál es la densidad de carga volumétrica?
(a)\(\textbf{E} = ax^{2}y^{2} \textbf{i}_{x}\)
b)\(\textbf{E} = a(\textbf{i}_{r} \cos \theta - \textbf{i}_{\theta} \sin \theta)\)
c)\(\textbf{E} = a(y \textbf{i}_{x} - x \textbf{i}_{y})\)
(d)\(\textbf{E} = (a/\textbf{r}^{2})[\textbf{i}_{\textrm{r}}(1 + \cos \phi) + \textbf{i}_{\phi} \sin \phi]\)
Encuentre la diferencia de potencial\(V\) entre las siguientes distribuciones de carga superficial:
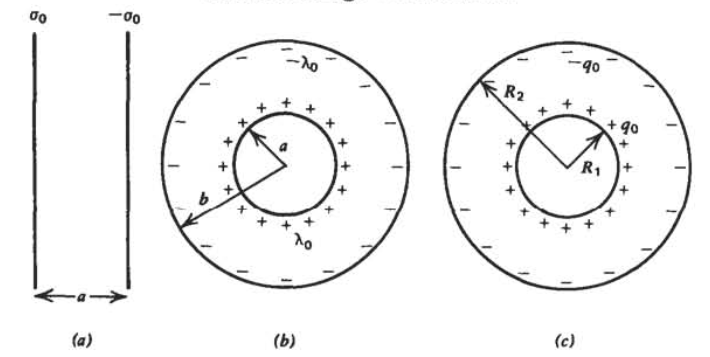
a) Dos láminas paralelas de carga superficial de polaridad opuesta\(\pm \sigma_{0}\) y espaciado\(a\).
(b) Dos cilindros coaxiales de carga superficial de longitud infinita y radios respectivos\(a\) y\(b\). La carga total por unidad de longitud en el cilindro interior es\(\lambda_{0}\) mientras que en el cilindro exterior es\(-\lambda_{0}\).
(c) Dos esferas concéntricas de carga superficial con radios respectivos\(R_1\) y\(R_2\). La esfera interna lleva una carga superficial uniformemente distribuida con carga total\(q_{0}\). La esfera exterior tiene carga total\(-q_{0}\).
Un hemisferio de radio\(R\) tiene una carga superficial uniformemente distribuida con carga total\(\mathcal{Q}\).
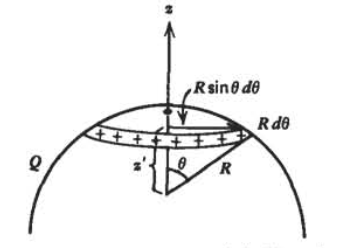
(a) Romper la superficie esférica en aros de carga de línea de espesor\(R d \theta\). ¿Cuál es el radio del aro, su altura\(z'\) y su carga incremental total\(dq\)?
b) ¿Cuál es el potencial a lo largo del\(z\) eje debido a este aro cargado incremental? Eliminar la dependencia\(\theta\) y expresar todas las variables en términos de\(z'\), la altura del aro diferencial de carga de línea.
(c) ¿Cuál es el potencial en cualquier posición a lo largo del\(z\) eje debido a todo el hemisferio de carga superficial? Insinuación:
\(\int \frac{dz'}{[a + bz']^{1/2}} = \frac{2\sqrt{a + bz'}}{b}\)
d) ¿Cuál es el campo eléctrico a lo largo del\(z\) eje?
(e) Si el hemisferio se carga uniformemente a lo largo de su volumen con carga total\(\), encuentre el potencial y el campo eléctrico en todos los puntos a lo largo del\(z\) eje. (Pista:\(\int r \sqrt{z^{2} + r^{2}} dr= \frac{1}{3} (z^{2} + r^{2})^{3/2}\).)
Dos cargas puntuales\(q_1\) y\(q_2\) se encuentran a lo largo del\(z\) eje a una distancia de\(a\) distancia.
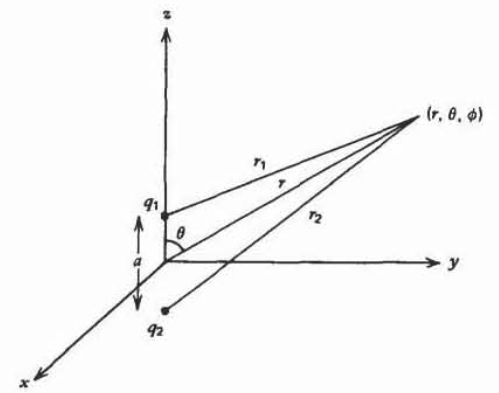
(a) Encontrar el potencial en la coordenada (\(r, \theta, \phi)\). (Pista:\(r_{1}^{2} = r^{2} + (a/2)^{2} -ar \cos \theta\).)
b) ¿Cuál es el campo eléctrico?
(c) Se forma un dipolo eléctrico si\(q_{2} = -q_{1}\). Encontrar una expresión aproximada para el campo potencial y eléctrico para puntos alejados del dipolo,\(r\gg a\).
(d) Cuál es la ecuación de las líneas de campo en este límite de campo lejano que está en todas partes tangente al campo eléctrico.
\(\frac{dr}{r d \theta} = \frac{E_{r}}{E_{\theta}}\)
Encuentra la ecuación de la línea de campo que pasa por el punto (\(r = r_{0}, \: \theta = \pi/2\)). (Pista:\(\int \cot \theta d \theta = \ln \sin \theta.\))
a) Encontrar los potenciales\(V_1\)\(V_2\), y\(V_3\) en la ubicación de cada una de las cargas de tres puntos que se muestran.
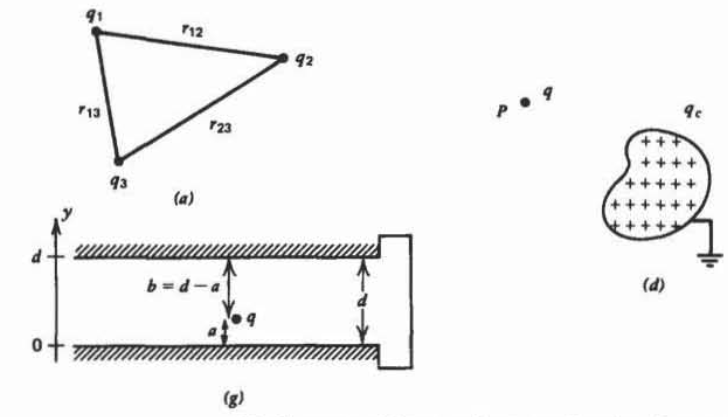
b) Consideremos ahora otro conjunto de cargas\(q'_{1}\) puntuales\(q'_{2}\) ,, y\(q'_{3}\) en las mismas posiciones y calcular los potenciales\(V'_{1}\),\(V'_{2}\), y\(V'_{3}\). Verificar por sustitución directa que
\(q'_{1}V_{1} + q'_{2}V_{2} + q'_{3}V_{3} = q_{1}V'_{1} + q_{2}V'_{2} + q_{3}V'_{3}\)
El resultado generalizado para cualquier número de cargos se llama teorema de reciprocidad de Green,
\(\sum_{i = 1}^{N} (q_{i}V'_{i}-q'_{i}V_{i}) = 0\)
(c) Demostrar que el teorema de reciprocidad de Green permanece inalterado para conductores perfectos ya que el potencial en el conductor es constante. El\(q_{i}\) es entonces la carga en el conductor.
d) Una carga\(q\) en el punto\(P\) se encuentra en las proximidades de un conductor de potencial cero. Se sabe que si el conductor se carga a una tensión\(V_c\), el potencial en el punto\(P\) en ausencia de la carga puntual es\(V_p\). Encuentre la carga total\(q_c\) inducida en el conductor conectado a tierra. (Pista: Let\(q_{1} = q, \: q_{2} = q_{c}, \: V_{2} = 0, \: q'_{1} = 0, \: V'_{1} = V_{p}, \: V'_{2} = V_{c}.\))
e) Si el conductor es una esfera de radio\(R\) y el punto\(P\) está a una\(D\) distancia del centro de la esfera, ¿qué es\(q_c\)? ¿Este resultado está relacionado con el método de las imágenes?
(f) Una carga de línea\(\lambda\) es una distancia\(D\) desde el centro de un cilindro de radio puesto a tierra\(a\). ¿Cuál es la carga total por unidad de longitud inducida en el cilindro?
(g) Una carga puntual\(q\) se encuentra entre dos conductores perfectos de potencial cero. ¿Cuál es la carga total inducida en cada superficie conductora? (Pista: Probar\(q_{1} = q, \: q_{2} = q(y=0), \: q_{3} = q(y = d), \: V_{2} = 0, \: V_{3} = 0, \: q'_{1} = 0, \: V'_{2} = V_{0}, \: V'_{3} = 0.\))
(h) Una carga puntual\(q\) viaja a velocidad constante\(v_{0}\) entre electrodos de placa paralelos cortocircuitados de espaciamiento\(d\). ¿Cuál es la corriente de cortocircuito en función del tiempo?
Sección 2.6
Una carga de línea infinitamente larga\(\lambda\) es una distancia\(D\) desde el centro de un cilindro conductor de radio\(R\) que lleva una carga total por unidad de longitud\(\lambda_{c}\). Cuál es la fuerza por unidad de longitud
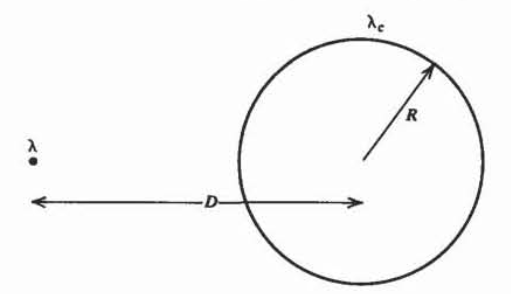
el cilindro? (Pista: ¿Dónde se puede colocar otra carga de imagen con el cilindro siendo una superficie equipotencial?)
Una hoja infinitamente larga de carga superficial de ancho\(d\) y densidad de carga uniforme\(\sigma_{0}\) se coloca en el\(yz\) plano.
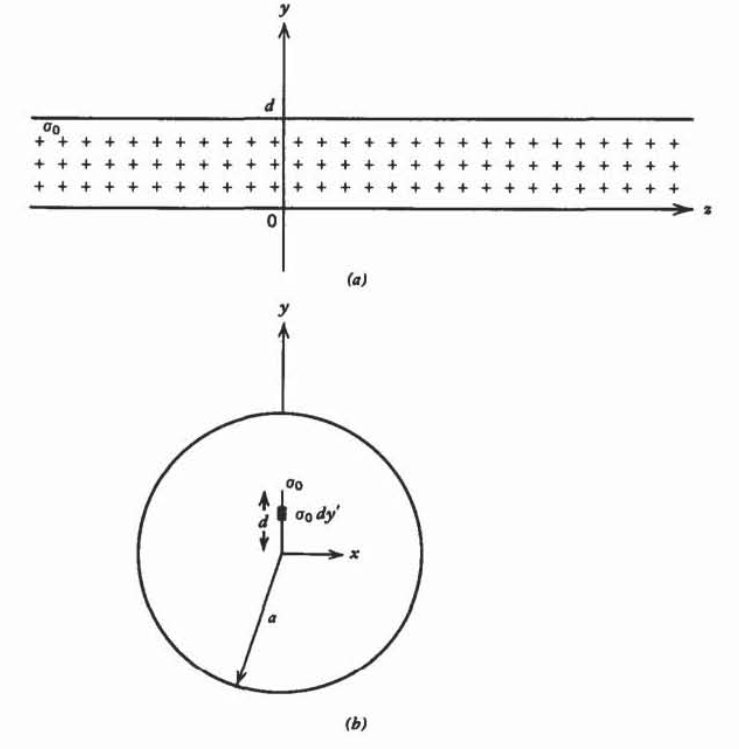
(a) Encontrar el campo eléctrico en todas partes del\(yz\) avión. (Pista: Romper la hoja en elementos diferenciales de carga de línea\(d \lambda = \sigma_{0} d y'.\))
(b) Un cilindro conductor infinitamente largo de radio a rodea la lámina cargada que tiene un lado a lo largo del eje del cilindro. Encuentra la carga de imagen y su ubicación debido a un elemento de carga de línea incremental\(\sigma_{0} dy'\) a distancia\(y'\).
(c) ¿Cuál es la fuerza por unidad de longitud sobre el cilindro? Insinuación:
\(\int \ln (1-cy')dy' = -(\frac{1-cy'}{c}) [\ln (1 - cy') - 1]\)
Una carga de línea\(\lambda\) se encuentra en coordenadas\(\left ( a,b \right )\) cerca de una esquina conductora en ángulo recto.
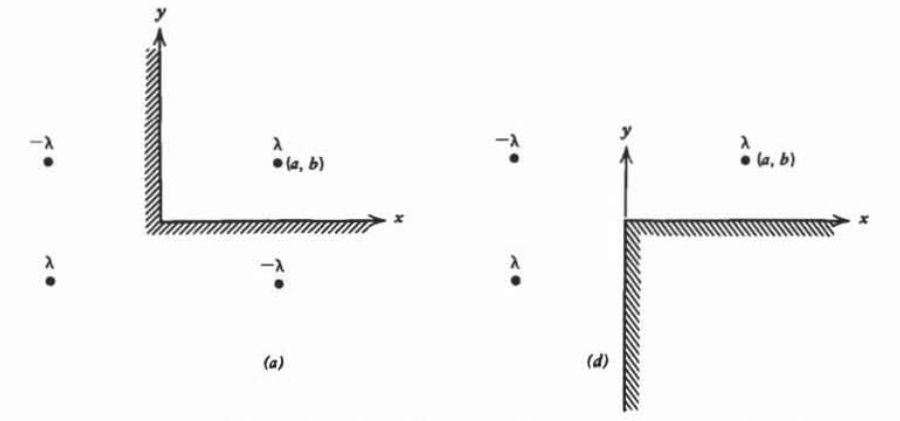
(a) Verificar que el uso de los tres cargos por líneas de imagen mostrados satisfaga todas las condiciones de contorno.
b) ¿Cuál es la fuerza por unidad de longitud\(\lambda\)?
c) ¿Qué carga por unidad de longitud se induce en las superficies\(x=0\) y\(y=0\)?
(d) Consideremos ahora el caso inverso cuando tres cargas de línea de polaridad alterna\(\pm \lambda\) están fuera de una esquina conductora. ¿Cuál es la fuerza sobre el conductor?
e) Repetir (a) - (d) con cargos puntuales.
Sección 2.7
Una carga de punto positivo\(q\) dentro de un campo eléctrico uniforme\(E_{0}\textrm{i}_{x}\) desde un plano conductor conectado a tierra.
a) ¿A qué valor de la fuerza sobre la carga\(x\) es igual a cero?
b) Si la carga se encuentra inicialmente en una posición igual a la mitad del valor que se encuentra en la letra a), ¿qué velocidad inicial mínima es necesaria para que continúe la carga\(x = = \infty\)? (Pista:\(E_{x} = - dV/dx\).)
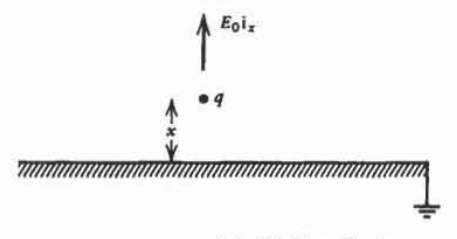
c) Si\(E_{0} = 0\), ¿cuánto trabajo es necesario para mover la carga puntual de\(x = d\) a\(x = + \infty\)?
Una esfera de radio\(R_2\) que tiene una carga superficial uniformemente distribuida\(\mathcal{Q}\) rodea una esfera de radio conectada a tierra\(R_1\).
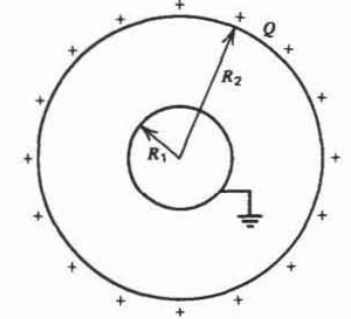
a) ¿Cuál es la carga total inducida en la esfera puesta a tierra? (Pista: Considere el cargo de imagen debido a un cargo incremental\(dq = (\mathcal{Q}/4 \pi) \sin \theta \,d \theta \,d \phi\) en\(r = R_{2}\).)
b) ¿Cuáles son las distribuciones potenciales y del campo eléctrico en todas partes?
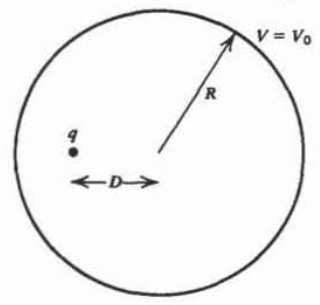
Una carga puntual\(q\) ubicada a una\(D\left ( D< R \right )\) distancia del centro se encuentra dentro de una esfera conductora de radio\(R\) que está a potencial constante\(V_0\). ¿En qué consiste la fuerza\(q\)?
Una carga de línea de longitud\(L\) con densidad uniforme\(\lambda_{0}\) se orienta de las dos vías mostradas con respecto a una esfera de radio puesta a tierra\(R\). Para ambos casos:
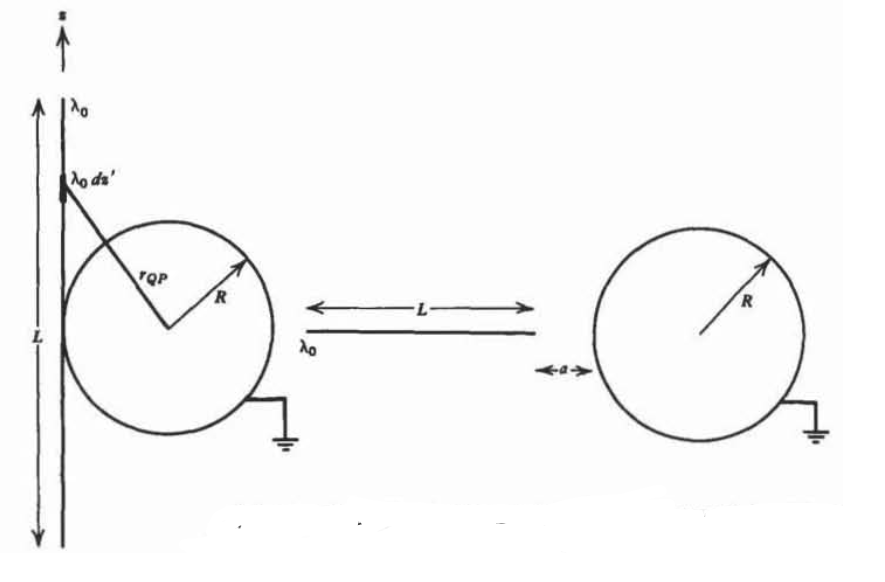
a) Considerar el elemento de carga incremental a\(\lambda_{0}dz'\) una\(r_{QP}\) distancia del centro de la esfera. ¿Cuál es su carga de imagen y dónde se encuentra?
b) ¿Cuál es la carga total inducida en la esfera? Insinuación:
\(\int \frac{dz'}{\sqrt{R^{2} + z'^{2}}} = \ln (z' + \sqrt{R^{2} + z'^{2}})\)
Una proyección hemisférica conductora de radio\(R\) se coloca sobre un plano de tierra de extensión infinita. Se\(d\) coloca una carga puntual a una distancia\(d\left ( d>R \right )\) por encima del centro del hemisferio.
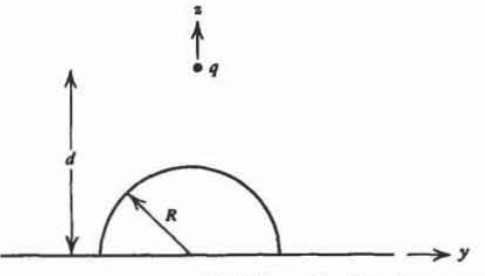
a) ¿En qué consiste la fuerza\(q\)? (Pista: Intente colocar tres cargas de imagen a lo largo del\(z\) eje para que el plano y el hemisferio tengan potencial cero.)
b) ¿Cuál es la carga total inducida en el hemisferio en\(r=R\) y en el plano de tierra\(\vert y \vert > R\)? Insinuación:
\(\int \frac{\textrm{r} d \textrm{r}}{[\textrm{r}^{2} + d^{2}]^{3/2}} = \frac{-1}{\sqrt{\textrm{r}^{2} + d^{2}}}\)
Una carga puntual\(q\) se coloca entre dos planos conductores paralelos conectados a tierra a una distancia de\(d\) distancia.
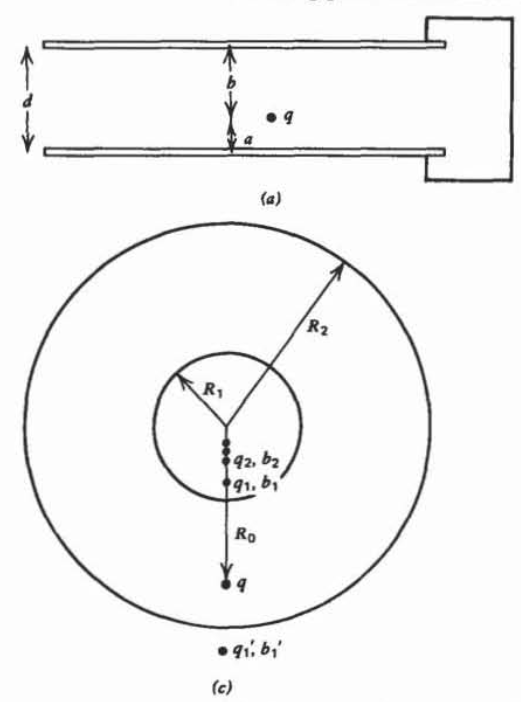
(a) La carga puntual a\(q\) una distancia\(a\) por encima del plano inferior y una distancia\(b\) por debajo del conductor superior tiene cargas de imagen ubicadas summétricamente. Sin embargo, cada carga de imagen en sí tiene una imagen en el conductor opuesto. Demuestre que es necesario un número infinito de cargos de imagen. ¿Cuáles son las ubicaciones de estos cargos por imagen?
(b) Demostrar que la carga total de cada conductor no puede ser encontrada por este método ya que la serie resultante es divergente.
(c) Consideremos ahora una carga puntual\(q\), una distancia radial\(R_0\) desde el centro de dos esferas conductoras concéntricas a tierra de radios\(R_1\) y\(R_2\). Mostrar que es necesario un número infinito de cargas de imagen en cada esfera donde, si denotamos la carga de imagen\(n\) th en la esfera más pequeña como\(q_n\) una distancia\(b_n\) desde el centro y la n ésima carga de imagen en la esfera exterior como\(q'_n\) una distancia\(b'_n\) del centro, luego
\(q_{n+1} = -\frac{R_{1}}{b'_{n}} q'_{n}, \: \: \: q'_{n+1} = -\frac{R_{2}}{b_{n}}q_{n} \\ b_{n+1} = \frac{R^{2}_{1}}{b'_{n}}, \: \: \: b'_{n+1} = \frac{R_{2}^{2}}{b_{n}}\)
(d) Demostrar que las ecuaciones de (c) pueden simplificarse para
\(q_{n+1} - q_{n-1} (\frac{R_{1}}{R_{2}}) = 0 \\ b_{n+1} - b_{n-1} (\frac{R_{1}}{R_{2}})^{2} =0 \)
e) Probar soluciones de ley de poder
\(q_{n} = A \lambda^{n}, \: \: \: \: b_{n} = B \alpha^{n}\)
y encontrar los valores característicos de\(\lambda\) y\(\alpha\) que satisfacen las ecuaciones en (d).
(f) Tomando una combinación lineal de las soluciones en (e), evaluar los coeficientes de amplitud desconocidos sustituyendo en valores por\(n = 1\) y\(n=2\). ¿Cuáles son todos los\(q_n\) y\(b_n\)?
g) ¿Cuál es la carga total inducida en la esfera interna?
(Pista:\(\sum_{n=1}^{\infty} a^{n} = a/(1-a) \textrm{ for } a < 1\))
(h) Utilizando las soluciones de (\(f\)) con las relaciones de diferencia de (c), encontrar\(q'_{n}\) y\(b'_{n}\).
(i) Demostrar que no\(\sum_{n=1}^{\infty} q'_{n}\) es una serie convergente para que la carga total sobre la esfera exterior no pueda ser encontrada por este método.
j) ¿Por qué debe ser la carga total inducida en ambas esferas\(-q\)? ¿Cuál es entonces la carga total inducida en la esfera exterior?
(k) Volviendo a nuestro problema original en (a) y (b) de una carga puntual entre planos paralelos, dejar que los radios de las esferas se acerquen al infinito de tal manera que las distancias
\(d = R_{2} - R_{1}, \: \: \: \: a = R_{2} -R_{0}, \: \: \: \: b=R_{0}-R_{1}\)
permanece finito. ¿Cuál es la carga total inducida en cada conductor plano?
Una carga puntual\(\mathcal{Q}\) es una distancia\(D\) por encima de un plano de tierra. Directamente debajo se encuentra el centro de una pequeña esfera conductora de radio\(R\) que descansa sobre el plano.
(a) Encontrar las primeras cargas de imagen y sus posiciones en la esfera y en el plano.
(b) Ahora encuentra la siguiente imagen de cada una inducida en la otra. Mostrar que se inducen dos conjuntos de cargas de imagen en la esfera donde cada uno obedece las ecuaciones de diferencia
\(q_{n+1} = \frac{q_{n}R}{2R-b_{n}}, \: \: \: b_{n+1} = \frac{R^{2}}{2R-b_{n}}\)
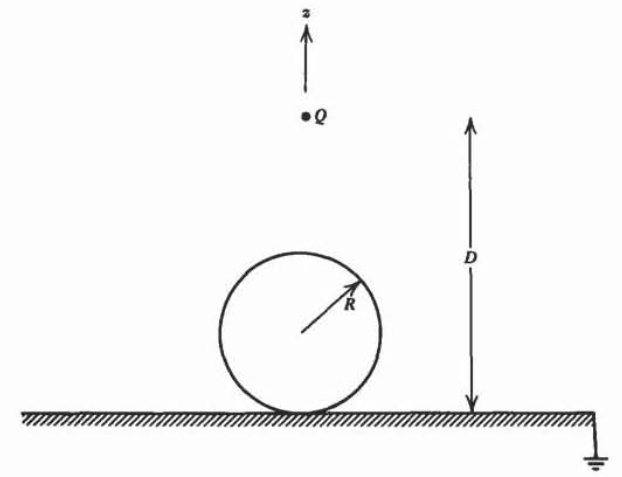
c) Eliminando el\(b_n\), demostrar que la ecuación de diferencia gobernante es
\(\frac{1}{q_{n+1}} - \frac{2}{q_{n}} + \frac{1}{q_{n-1}} = 0\)
Adivina soluciones de la forma
\(P_{n} = 1/q_{n} = A \lambda^{n}\)
y encontrar los valores permitidos de\(\lambda\) que satisfagan la ecuación de diferencia. (Pista: Para las raíces dobles de\(\lambda\) las soluciones totales es de la forma\(P_{n} = (A_{1} + A_{2}n)\lambda^{n}.\))
(d) Encontrar todas las cargas de imagen y sus posiciones en la esfera y en el plano.
(e) Escribir la carga total inducida n la esfera en la forma
\(q_{T} = \sum_{n=1}^{\infty} \frac{A}{[1-an^{2}]}\)
¿Qué son\(A\) y\(a\)?
f) Deseamos generalizar este problema al de una esfera que descansa sobre el plano del suelo con un campo aplicado\(\textbf{E}= -E_{0}\textbf{i}_{x}\) en el infinito. ¿Cuál debe\(\mathcal{Q}/D^{2}\) ser la relación, de tal manera que como\(\) y\(D\) llegar a ser infinito el campo lejos de la esfera en el\(\theta = \pi/2\) plano es\(-E_{0}\textbf{i}_{x}\)?
g) En este límite ¿cuál es la carga total inducida en la esfera? (Pista:\(\sum_{n=1}^{\infty} \frac{1}{n^{2}} = \pi^{2}/6\).)
Una esfera conductora de radio\(R\) en el potencial\(V_0\) tiene su centro a una distancia\(D\) de un plano infinito conectado a tierra.
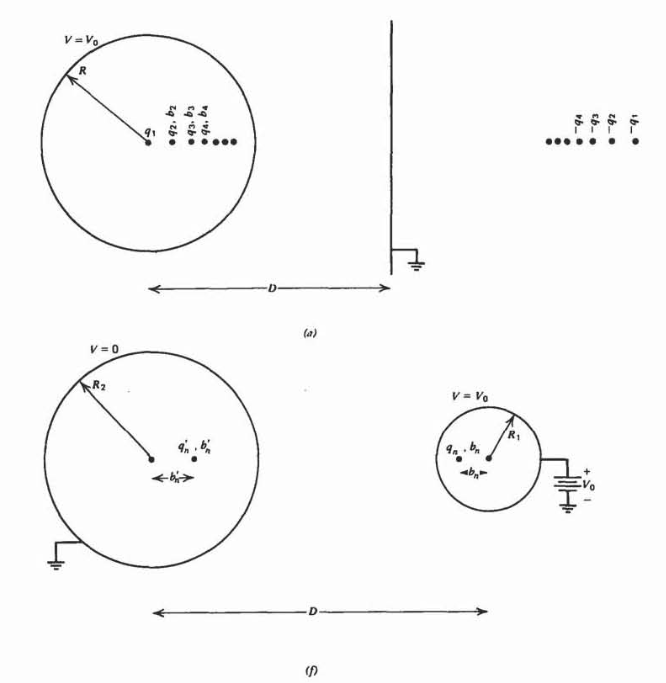
(a) Demostrar que un número infinito de cargas de imagen en el plano y en la esfera son necesarias para satisfacer las condiciones de contorno
\(q_{n} = \frac{q_{n-1}R}{2D-b_{n-1}}, \: \: \: \: b_{n}= \frac{R^{2}}{2D-b_{n-1}}\)
¿Qué son\(q_1\) y\(q_2\)?
(b) Demostrar que la ecuación de diferencia gobernante es
\(\frac{1}{q_{n-1}} - \frac{c}{q_{n}} + \frac{1}{q_{n+1}} = 0\)
¿Qué es\(c\)?
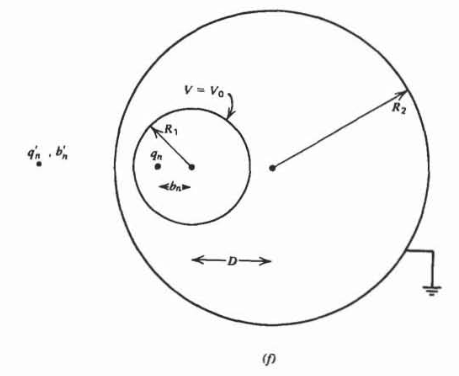
(c) Resolver la ecuación de diferencia en (b) asumiendo soluciones de la forma
\(P_{n} = 1/q_{n} = A \lambda^{n}\)
¿Qué valores de\(\lambda\) satisfacer (b)? Insinuación:
\(c/2 + \sqrt{(c/2)^{2}-1} = \frac{1}{c/2 - \sqrt{(c/2)^{2}-1}}\)
(d) ¿Cuál es la posición de cada carga de imagen? ¿Cuál es la posición límite de los cargos de imagen como\(n \rightarrow \infty\)?
(e) Demostrar que la capacitancia (la relación entre la carga total en la esfera y la tensión\(V_0\)) puede escribirse como una serie infinita
\(C = C_{0}(\lambda^{2}-1)(\frac{1}{\lambda^{2}-1} + \frac{\lambda}{\lambda^{4}-1} + \frac{\lambda^{2}}{\lambda^{6} -1} + \frac{\lambda^{3}}{\lambda^{8}-1} + ... )\)
¿Qué son\(C_0\) y\(\lambda\)?
(f) Demostrar que las cargas de imagen y sus posiciones para dos esferas obedecen a las ecuaciones de diferencia
\(q_{n+1} = \mp \frac{q'_{n}R_{1}}{D-b'_{n}}, \: \: \: \: b_{n+1} = \pm \frac{R_{1}^{2}}{D-b'_{n}} \\ q'_{n} = -\frac{R_{2}q_{n}}{D \mp b_{n}}, \: \: \: \: b'_{n} = \frac{R_{2}^{2}}{D \mp b_{n}}\)
donde usamos los signos superiores para la esfera adyacente y los signos inferiores cuando la esfera de radio más pequeña\(R_1\) está dentro de la más grande.
(g) Demostrar que la ecuación de diferencia gobernante es de la forma
\(P_{n+1} \mp cP_{n} + P_{n-1} = 0\)
¿Qué son\(P_n\) y\(c\)?
(h) Resolver (g) asumiendo soluciones de la forma
\(P_{n} = A \lambda^{n}\)
(i) Demostrar que la capacitancia es de la forma
\(C = C_{0}(1 - \xi^{2}) (\frac{1}{1-\xi^{2}} + \frac{\lambda}{1 - \xi^{2}\lambda^{2}} + \frac{\lambda^{2}}{1 - \xi^{4}\lambda^{4}} + ...)\)
¿Qué son\(C_0\)\(\xi\), y\(\lambda\)?
(j) Cuál es la capacitancia cuando las dos esferas son concéntricas de manera que eso\(D=0\). (Pista:\(\sum_{n=0}^{\infty} a^{n} = 1/(1-a) \textrm{ for } a<1\).)


