4.6: Problemas
- Page ID
- 86730
Sección 4.2
El sistema de electrodos hiperbólicos de la Sección 4-2-2a solo se extiende sobre el rango\(0 \leq x \leq x_{0}, \: 0 \leq y \leq y_{0}\) y tiene una profundidad\(D\).
a) Despreciando los efectos de campo de franjas ¿cuál es la capacitancia aproximada?
(b) Una pequeña carga de prueba positiva\(q\) (los efectos de carga de imagen son insignificantes) con masa\(m\) se libera del resto de la superficie del electrodo hiperbólico en\(x = x_{0}\),\(y = ab/x_{0}\). ¿Cuál es la velocidad de la carga en función de su posición?
(c) Cuál es la velocidad de la carga cuando golpea el electrodo opuesto
Una hoja de carga de superficie libre en\(x = 0\) tiene distribución de carga
\(\sigma_{f} = \sigma_{0} \cos a y\)
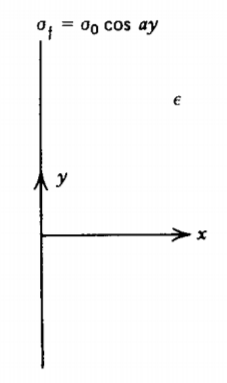
a) ¿Cuáles son las distribuciones de potencial y campo eléctrico?
b) ¿Cuál es la ecuación de las líneas de campo?
Dos láminas de polaridad opuesta con sus distribuciones de potencial restringidas están\(d\) separadas a una distancia.
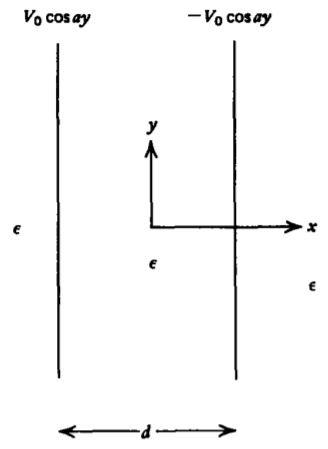
a) ¿Cuáles son las distribuciones de potencial y campo eléctrico en todas partes?
b) ¿Cuáles son las distribuciones de carga superficial en cada hoja?
Una caja rectangular conductora de ancho\(d\) y largo\(l\) es de extensión infinita en la dirección z. El potencial a lo largo del\(x = 0 \) borde es\(V_1\) mientras todas las demás superficies están puestas a tierra (\(V_{2} = V_{3} = V_{4} = 0\)).
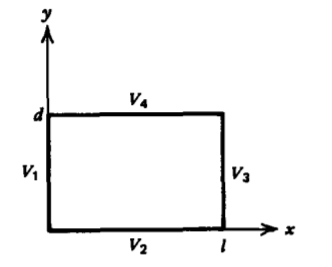
a) ¿Cuáles son las distribuciones de potencial y campo eléctrico?
b) El potencial at\(y = 0\) se eleva ahora a\(V_2\) mientras la superficie\(x =0\) permanece en el potencial\(V_1\). Las otras dos superficies permanecen a potencial cero (\(V_{3} = V_{4} = 0\)). ¿Cuáles son las distribuciones de potencial y campo eléctrico? (Pista: Usar superposición.)
(c) ¿Cuál es la distribución de potencial si cada lado está respectivamente a potenciales distintos de cero \(V_1\),\(V_2\), \(V_3\), y \(V_4\)?
Una lámina con distribución potencial
\(V = V_{0} \sin a x \cos bz\)
se coloca paralelo y entre dos conductores paralelos a tierra a una\(d\) distancia de distancia Es una distancia\(s\) por encima del plano inferior.
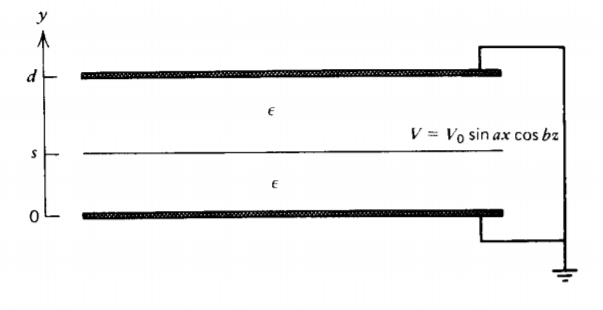
a) ¿Cuáles son las distribuciones de potencial y campo eléctrico? (Pista: Puede escribir la distribución potencial mediante inspección usando una función hiperbólica desplazada espacialmente\(\sinh c\left ( y-d \right )\).)
b) ¿Cuál es la distribución de carga superficial en cada plano en\(y=0\)\(y=s\), y\(y=d\)?
Una carga superficial uniformemente distribuida\(\sigma_{0}\) de ancho\(d\) y de extensión infinita en la\(z\) dirección se coloca en\(x= 0\) perpendicular a dos planos paralelos de espaciado a tierra\(d\).
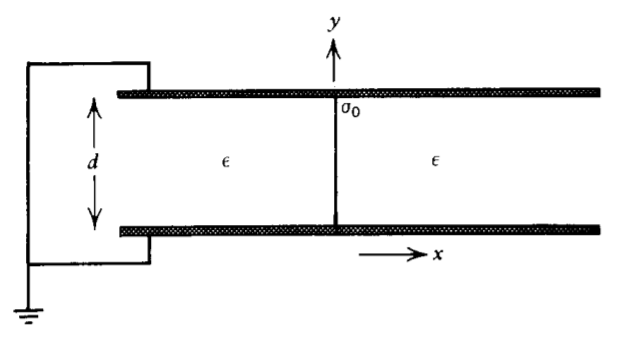
a) ¿Cuáles son las distribuciones de potencial y campo eléctrico? (Pista: Escribir\(\sigma_{0}\) como una serie de Fourier.)
b) ¿Cuál es la distribución de carga superficial inducida en cada plano?
c) ¿Cuál es la carga total inducida por unidad de longitud en cada plano? Pista:
\[\sum_{n=1 // n \textrm{ odd}}^{\infty} \frac{1}{n^{2}} = \frac{\pi^{2}}{8} \nonumber \]
Una losa de carga volumétrica de espesor\(d\) con densidad de carga volumétrica\(\rho_{f} = \rho_{0} \sin ax\) se coloca sobre un plano de tierra conductor.
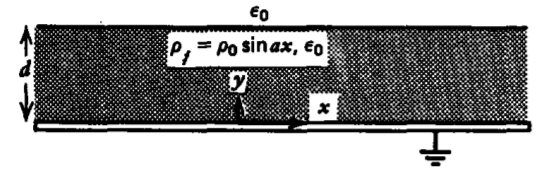
(a) Encontrar una solución particular a la ecuación de Poisson. ¿Se cumplen las condiciones de límite?
b) Si la solución a a) no satisface todas las condiciones límite, añadir una solución laplaciana que sí.
c) ¿Cuál es la distribución del campo eléctrico en todas partes y la distribución de carga superficial en el plano de tierra?
d) ¿Cuál es la fuerza por unidad de longitud sobre la carga volumétrica y en el plano de tierra para una sección de ancho\(2 \pi/a\)? ¿Son iguales estas fuerzas?
e) Repetir (a) - (c), si en lugar de carga gratuita, la losa es un medio polarizado permanentemente con polarización
\(\textbf{P} = P_{0} \sin ax \textbf{i}_{y}\)
Considerar las coordenadas cartesianas\(x,y\) y definir la cantidad compleja
\(z = x + jy, \: \: \: \: j = \sqrt{-1}\)
donde z no debe confundirse con la coordenada cartesiana. Cualquier función de\(z\) también tiene partes reales e imaginarias
\(w(z) = u (x,y) + jv (x,y)\)
a) Encontrar\(u\) y\(v\) para las siguientes funciones:
i)\(z^{2}\)
ii)\(\sin z\)
iii)\(\cos z\)
iv)\(e^{z}\)
v)\(\ln z \)
b) Darse cuenta de que las derivadas parciales de\(w\) son
\(\frac{\partial w}{\partial x} = \frac{dw}{d z} \frac{\partial z}{\partial x} = \frac{d w}{dz} = \frac{\partial u}{\partial x} + j \frac{\partial v}{\partial x} \\ \frac{\partial w}{\partial y} = \frac{d w}{dz} \frac{\partial z}{\partial y} = j \frac{dw}{dz} = \frac{\partial u}{\partial y} + j \frac{\partial v}{\partial y}\)
demostrar que\(u\) y\(v\) debe estar relacionado como
\(\frac{\partial u}{\partial x} = \frac{\partial v}{\partial y}, \: \: \: \frac{\partial u}{\partial y} = - \frac{\partial v}{\partial x}\)
Estas relaciones se conocen como ecuaciones de Cauchy-Riemann\(u\) y\(v\) se denominan funciones conjugadas.
(c) Demostrar que ambos\(u\) y\(v\) obedecer la ecuación de Laplace.
(d) Mostrar que las líneas de constante\(u\) y\(v\) son perpendiculares entre sí en el\(xy\) plano. (Pista: ¿Son\(\nabla u\) vectores\(\nabla v\) perpendiculares?)
Sección 4.3
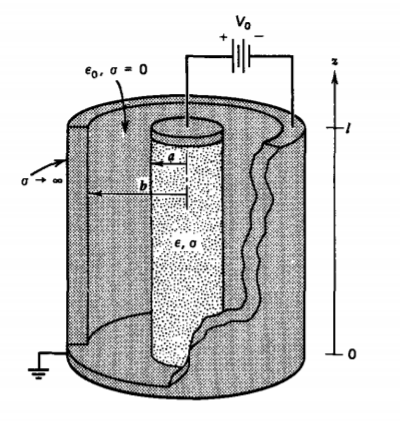
Una carcasa semicilíndrica de longitud\(l\) que tiene radio interior\(a\) y radio exterior\(b\) está compuesta por dos materiales dieléctricos con pérdida diferentes (\(\varepsilon_{1}, \: \sigma_{1}\)) para\(0 < \phi < \alpha\) y (\(\varepsilon_{2}, \: \sigma_{2}\)) para\(\alpha < \phi < \pi\). Se aplica un voltaje\(V_{0}\) de paso a\(t = 0\). Variaciones de descuido con\(z\).
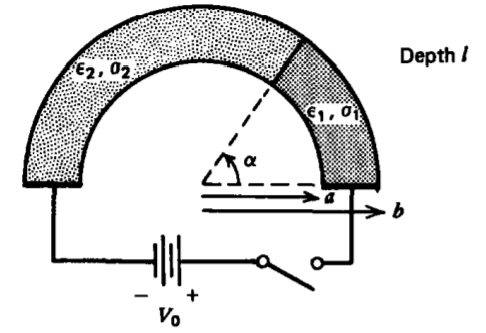
a) ¿Cuáles son las distribuciones de potencial y campo eléctrico dentro del proyectil a veces \(t =0\)\(t = \infty\), y durante el intervalo transitorio? (Pista: Asumir potenciales de los efectos de forma\(V(\phi) = A(t) \phi + B(t)\) y descuido de la región fuera de la concha semicilíndrica.)
b) ¿Cuál es la dependencia temporal de la carga superficial\(\phi = \alpha\)?
c) ¿Cuál es la resistencia y capacitancia?
El potencial en un cilindro infinitamente largo está limitado a ser
\(V (\textrm{r} = a) = V_{0} \sin n \phi\)
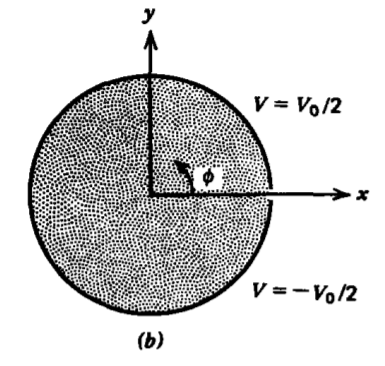
(a) Encontrar el potencial y el campo eléctrico en todas partes.
b) Ahora se cambia el potencial para que sea constante en cada mitad del cilindro:
\(V(\textrm{r} = a. \phi) = \left \{ \begin{matrix} V_{0}/2, & 0 < \phi < \pi \\ - V_{0}/2, & \pi < \phi < 2 \pi \end{matrix} \right.\)
Escribe esta onda cuadrada de potencial en una serie de Fourier.
(c) Utilizar los resultados de (a) y (b) para encontrar el potencial y el campo eléctrico debido a esta onda cuadrada de potencial.
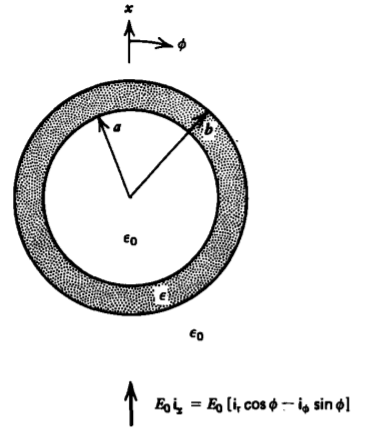
Una carcasa dieléctrica cilíndrica de radio interior a y radio exterior\(b\) se coloca en el espacio libre dentro de un campo eléctrico uniforme\(E_{0} \textbf{i}_{x}\). ¿Cuáles son las distribuciones de potencial y campo eléctrico en todas partes?
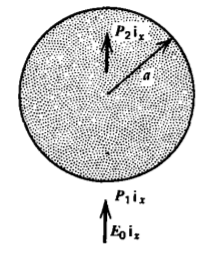
Un cilindro permanentemente polarizado\(P_{2}\textbf{i}_{x}\) de radio a se coloca dentro de un medio polarizado\(P_{1}\textbf{i}_{x}\) de extensión infinita. Se aplica un campo\(E_{0}\textbf{i}_{x}\) eléctrico uniforme al infinito. No hay cargo gratuito en el cilindro. ¿Cuáles son las distribuciones de potencial y campo eléctrico?
Un tipo de precipitador electrostático tiene un cilindro de radio perfectamente conductor\(a\) colocado dentro de un campo eléctrico uniforme\(E_{0} \textbf{i}_{x}\). Un flujo uniforme de iones positivos con carga\(q_0\) y densidad numérica\(n_0\) se inyectan al infinito y viajan a lo largo de las líneas de campo con movilidad\(\mu\). Aquellas líneas de campo que se acercan al cilindro con iones de\(E_{\textrm{r}}< 0\) depósito, los cuales se redistribuyen uniformemente sobre la superficie del cilindro. El campo propio debido a la carga inyectada es insignificante en comparación con \(E_0\).
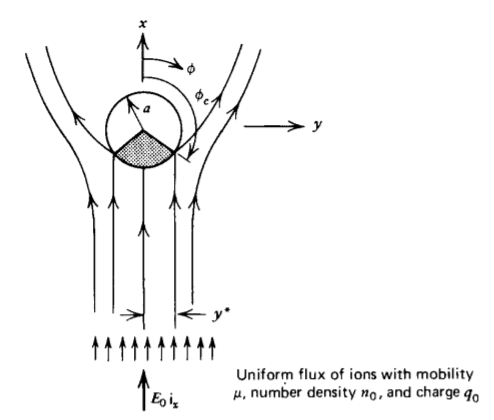
a) Si la carga distribuida uniformemente por unidad de longitud en el cilindro es\(\lambda(t)\), ¿cuál es la distribución de campo? ¿Dónde está el campo eléctrico cero? Este punto se llama punto crítico porque los iones que fluyen más allá de un lado de este punto pierden el cilindro mientras que los del otro lado se recogen. ¿Qué ecuación obedecen las líneas de campo? (Pista: A la solución de campo de la Sección 4-3-2a, agregue el campo debido a una carga de línea)\(\lambda\).
(b) Sobre qué rango de ángulo\(\phi\),\(\phi_{c} < \phi < 2 \pi - \phi_{c}\), ¿hay una ventana (región sombreada en la figura) para el cobro de cargos en función de\(\lambda (t)\)? (Pista:\(E_{\textrm{r}}< 0\) para cobro de cargos.)
c) ¿Cuál es la cantidad máxima de carga por unidad de longitud que se puede recoger en el cilindro?
d) ¿Cuál es la corriente de carga del cilindro por unidad de longitud? (Pista:\(dI = -q_{0} n_{0} \mu E_{r} a d \phi\))
e)\(\phi = \pi\) ¿En qué rango de\(y=y^{\ast }\), a\(\textrm{r}=\infty \), los iones inyectados impactan en el cilindro en función de\(\lambda (t)\)? ¿Cuál es esta corriente de carga por unidad de longitud? Comparar con (d).
Se permite que el cilindro de la Sección 4-3-2 colocado dentro de un medio con pérdida alcance el estado estacionario.
(a) En\(t = 0\) el campo eléctrico impuesto al infinito se pone repentinamente a cero. ¿Cuál es la dependencia temporal de la distribución de carga superficial\(\textrm{r} = a\)?
(b) Encontrar la distribución de carga superficial si el campo al infinito es una función sinusoidal del tiempo\(E_{0} \cos \omega t\)
Una lata cilíndrica perfectamente conductora de radio\(c\) abierta en un extremo tiene su superficie interior recubierta con una capa resistiva. La parte inferior\(z = 0\) y un poste central de radio perfectamente conductor\(a\) están a potencial cero, mientras que\(V_0\) se impone un potencial constante en la parte superior de la lata.
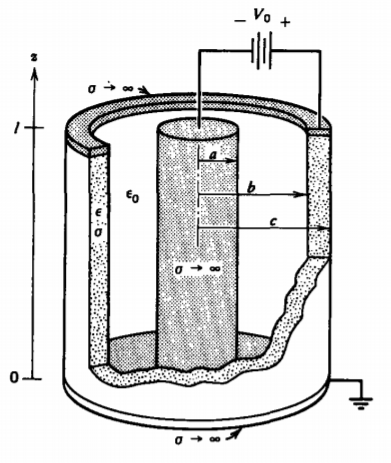
a) ¿Cuáles son las distribuciones de potencial y campo eléctrico dentro de la estructura\(\left ( a< \textrm{r}< c,0< z< l \right )\)? (Pista: Pruebe las soluciones constantes de separación cero\(n = 0\),\(k =0\).)
b) ¿Cuál es la distribución de carga superficial y la carga total a\(\textrm{r}=a\)\(\textrm{r}=b\), y\(z =0\)?
c) ¿Cuál es la ecuación de las líneas de campo en la región del espacio libre?
Un cilindro conductor óhmico de radio\(a\) está rodeado por una lata cilíndrica perfectamente conductora puesta a tierra de radio\(b\) abierta en un extremo. \(V_0\)Se aplica un voltaje en la parte superior del cilindro resistivo. Variaciones de descuido con\(\phi\).
a) ¿Cuáles son las distribuciones de potencial y campo eléctrico dentro de la estructura,\(0< z < l\),\(0 <\textrm{r}< b\)? (Pista: Pruebe las soluciones constantes de separación cero\(n = 0\),\(k = 0\) en cada región.)
b) ¿Cuál es la distribución de carga superficial y la carga total en la interfaz\(r = a\)?
c) ¿Cuál es la ecuación o las líneas de campo en la región del espacio libre?
Sección 4.4
Un hemisferio de radio perfectamente conductor\(R\) se coloca sobre un plano de tierra de extensión infinita. Se\(E_{0} \textbf{i}_{z}\) aplica un campo uniforme al infinito.
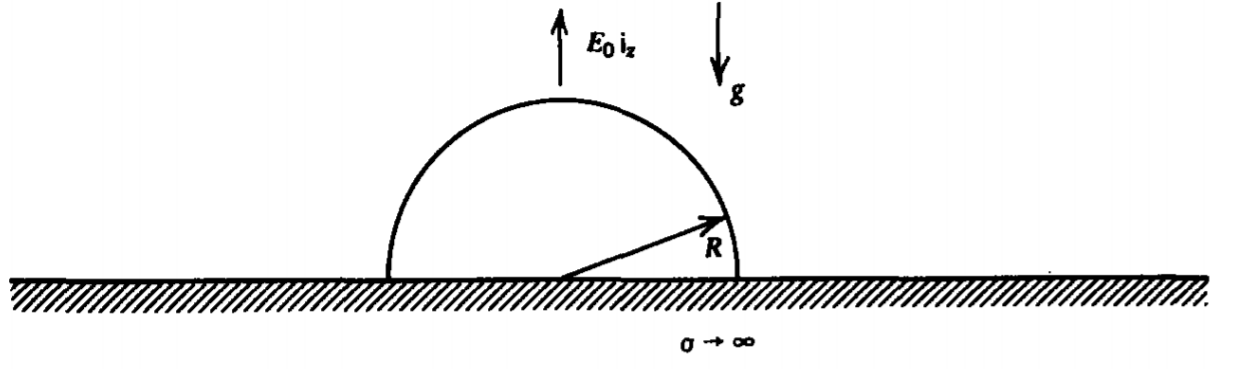
(a) Cuanta más carga hay en el hemisferio que la que habría en el plano sobre el área ocupada por el hemisferio.
b) Si el hemisferio tiene densidad de masa\(\rho_{m}\) y se encuentra en un campo de gravedad\(-g \textbf{i}_{z}\), ¿qué tan grande debe\(\) ser para levantar el hemisferio? Pista:
\(\int \sin \theta \cos^{m} \theta d \theta = - \frac{\cos^{m+1} \theta}{m + 1}\)
Una esfera de radio\(R\), permitividad\(\varepsilon_{2}\) y conductividad óhmica\(\sigma_{2}\) se coloca dentro de un medio de permitividad\(\varepsilon_{1}\) y conductividad\(\sigma_{1}\),. Un campo eléctrico uniforme\(E_{0} \textbf{i}_{z}\) se enciende repentinamente a las\(t = 0\).
a) ¿Cuáles son las condiciones límite e iniciales necesarias?
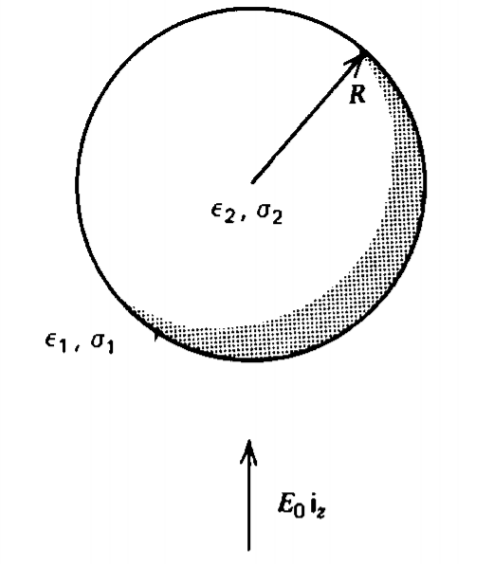
b) ¿Cuáles son las distribuciones de potencial y campo eléctrico en función del tiempo?
c) ¿Cuál es la carga superficial \(r = R\)?
d) Repetir (b) y (c) si el campo aplicado varía sinusoidalmente con el tiempo como\(E_{0} \cos \omega t\) y ha estado encendido mucho tiempo.
La distribución de carga superficial en una esfera dieléctrica con permitividad\(\varepsilon_{2}\) y radio R es
\(\sigma_{f} = \sigma_{0} (3 \cos^{2} \theta -1)\)
El medio circundante tiene permitividad\(\varepsilon_{1}\). ¿Cuáles son las distribuciones de potencial y campo eléctrico? (Pista: Prueba las\(n = 2\) soluciones.
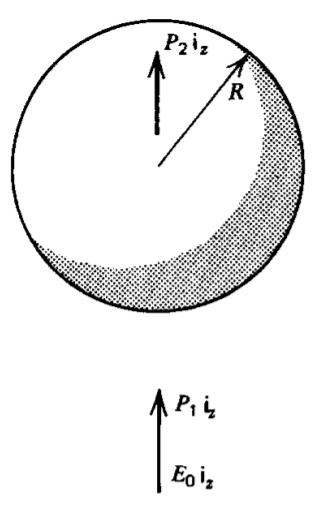
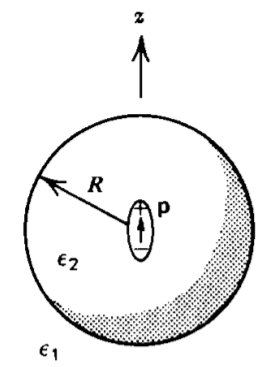
Una esfera\(P_{2} \textbf{i}_{z}\) de radio polarizada permanentemente\(R\) se coloca dentro de un medio polarizado\(P_{1} \textbf{i}_{z}\). Se aplica un campo\(E_{0} \textbf{i}_{z}\) eléctrico uniforme al infinito. No hay cargo gratuito en\(r = R\). ¿Cuáles son las distribuciones de potencial y campo eléctrico?
Un dipolo puntual\(\textbf{p} = p \textbf{i}_{z}\), se coloca en el centro de una esfera dieléctrica que está rodeada por un medio dieléctrico diferente. No hay ningún cargo de superficie libre en la interfaz. ¿Cuáles son las distribuciones de potencial y campo eléctrico? Pista:
\(\lim_{r \rightarrow 0} V (r, \theta) = \frac{p \cos \theta}{4 \pi \varepsilon_{2} r^{2}}\)
Sección 4.5
La caja conductora con lados de longitud\(d\) en la Sección 4-5-2 se llena con una distribución uniforme de carga volumétrica con densidad
\(\rho_{0} = - \frac{72 \varepsilon_{0}}{d^{2}} [ \textrm{coul m}^{-3}]\)
¿Cuáles son los potenciales en los cuatro puntos interiores cuando el exterior de la caja está conectado a tierra?
Repita el procedimiento de relajación de la Sección 4-5-2 si los potenciales límite son:
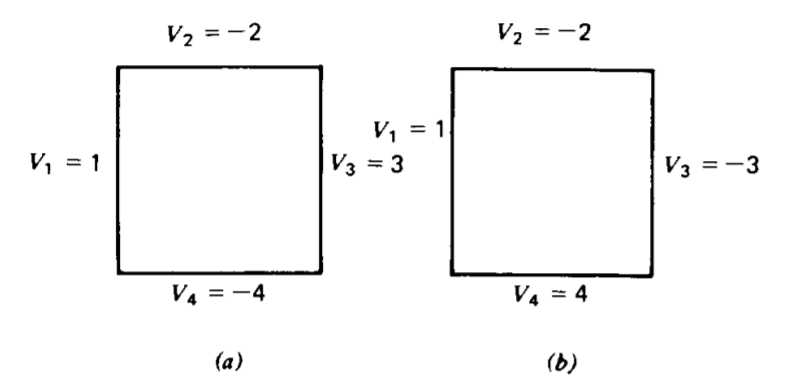
(a)\(V_1\) = 1,\(V_2\) = -2,\(V_3\) = 3,\(V_4\) = -4
(b)\(V_1\) = 1,\(V_2\) = -2,\(V_3\) = -3,\(V_4\) = 4
(c) Comparar con cuatro decimales con la solución exacta.


