5.8: Campos magnéticos y fuerzas

5-8-1 Medios magnetizables

Un medio magnetizable que transporta una corriente libre\(\textbf{J}_{f}\) se coloca dentro de un campo magnético\(\textbf{B}\), el cual es una función de la posición. Además de la fuerza Lorentz, el medio siente las fuerzas en todos sus dipolos magnéticos. Enfoca la atención en el dipolo magnético rectangular que se muestra en la Figura 5-26. La fuerza en cada pata portadora de corriente es

\[\textbf{f} = \textbf{i} dl \times (B_{x} \textbf{i}_{x} + B_{y} \textbf{i}_{y} + B_{z} \textbf{i}_{z}) \\ \Rightarrow \textbf{f}(x) = - i \Delta y [ -B_{x} \textbf{i}_{z} + B_{z} \textbf{i}_{x}] \big|_{x} \\ \textbf{f}(x + \Delta x) = i \Delta y [ - B_{x} \textbf{i}_{z} + B_{z} \textbf{i}_{x}] \big|_{x + \Delta x} \\ \textbf{f} (y) = i \Delta x [B_{y} \textbf{i}_{z} - D_{z} \textbf{i}_{y}] \big|_{y} \\ \textbf{f} (y + \Delta y) = -i \Delta x [ B_{y} \textbf{i}_{z} - B_{z} \textbf{i}_{y}] \big|_{y + \Delta y} \nonumber \]

de manera que la fuerza total sobre el dipolo sea

\[\textbf{f} = \textbf{f} (x) + \textbf{f} (x + \Delta x) + \textbf{f} (y) + \textbf{f} ( y + \Delta y) \\ = - \Delta x \Delta y \bigg[ \frac{B_{z} (x + \Delta x) - B_{z} (x)}{\Delta x} \textbf{i}_{z} - \frac{B_{x} (x + \Delta x) - B_{x} (x)}{\Delta x} \textbf{i}_{z} + \frac{B_{z}(y + \Delta y) - B_{z} (y)}{\Delta y} \textbf{i}_{y} - \frac{B_{y}(y + \Delta y) - B_{y} (y)}{\Delta y} \textbf{i}_{z} \bigg] \nonumber \]

Figura 5-26 Un dipolo magnético en un campo magnético B.

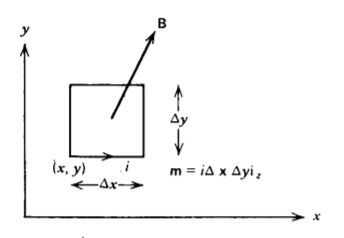
En el límite de infinitesimal\(\Delta x\) y\(\Delta y \) los términos entre corchetes definen derivadas parciales mientras que el coeficiente es solo el momento dipolo magnético\(\textbf{m} = i \Delta x \Delta y \textbf{i}_{z}\):

\[\lim_{\Delta x \rightarrow 0 \\ \Delta y \rightarrow 0} \textbf{f} = m_{z} \bigg[ \frac{\partial B_{z}}{\partial x} \textbf{i}_{x} - \bigg( \frac{\partial B_{x}}{\partial x} + \frac{\partial B_{y}}{\partial y} bigg) \textbf{i}_{z} + \frac{\partial B_{z}}{\partial y} \textbf{i}_{y} \bigg] \nonumber \]

La ley de Ampere y Gauss para el campo magnético relaciona los componentes del campo como

\[\nabla \cdot \textbf{B} = 0 \Rightarrow \frac{\partial B_{z}}{\partial z} = - \bigg( \frac{\partial B_{z}}{\partial x} + \frac{\partial B_{y}}{\partial y} \bigg) \nonumber \]

\[\nabla \times \textbf{B} = \mu_{0}(\textbf{J}_{f} + \nabla \times \textbf{M}) = \mu_{0} \textbf{J}_{T} \Rightarrow \frac{\partial B_{z}}{\partial y} - \frac{\partial B_{y}}{\partial z} = \mu_{0} J_{Tx} \\ \frac{\partial B_{x}}{\partial z} - \frac{\partial B_{z}}{\partial x} = \mu_{0} J_{Ty} \\ \frac{\partial B_{y}}{\partial x} - \frac{\partial B_{x}}{\partial y} = \mu_{0}J_{Tz} \nonumber \]

que pone (3) en la forma

\[\textbf{f} = m_{z} \bigg( \frac{\partial B_{x}}{\partial z} \textbf{i}_{x} + \frac{\partial B_{y}}{\partial z} \textbf{i}_{y} + \frac{\partial B_{z}}{\partial z} \textbf{i}_{z} - \mu_{0}(J_{Ty} \textbf{i}_{x} - J_{Tx} \textbf{i}_{y}) \bigg) \\ = (\textbf{m} \cdot \nabla) \textbf{B} + \mu_{0} \textbf{m} \times \textbf{J}_{T} \nonumber \]

donde\(\textbf{J}_{T}\) está la suma de corrientes libres y de magnetización.

Si hay N dipolos por unidad de volumen, la densidad de fuerza en los dipolos y en la corriente libre es

\[\textbf{F} = N \textbf{f} = ( \textbf{M} \cdot \nabla) \textbf{B} + \mu_{0} \textbf{M} \times \textbf{J}_{T} + \textbf{J}_{f} \times \textbf{B} \\ = \mu_{0} (\textbf{M} \cdot \nabla) ( \textbf{H} + \textbf{M}) + \mu_{0} \textbf{M} \times (\textbf{J}_{f} + \nabla \times \textbf{M}) + \mu_{0} \textbf{J}_{f} \times (\textbf{H} + \textbf{M}) \\ = \mu_{0} (\textbf{M} \cdot \nabla) (\textbf{H} + \textbf{M}) + \mu_{0} \textbf{M} \times (\nabla \times \textbf{M}) + \mu_{0} \textbf{J}_{f} \times \textbf{H} \nonumber \]

Uso de la identidad del vector

\[\textbf{M} \times (\nabla \times \textbf{M}) = - (\textbf{M} \cdot \nabla) \textbf{M} + \frac{1}{2} \nabla (\textbf{M} \cdot \textbf{M}) \nonumber \]

(7) se puede reducir a

\[\textbf{F} = \mu_{0} (\textbf{M} \cdot \nabla) \textbf{H} + \mu_{0} \textbf{J}_{f} \times \textbf{H} + \nabla \bigg( \frac{\mu_{0}}{2} \textbf{m} \cdot \textbf{M} \bigg) \nonumber \]

La fuerza total sobre el cuerpo es solo el volumen integral de F:

\[\textbf{f} = \int_{\textrm{V}} \textbf{F} d \textrm{V} \nonumber \]

En particular, la última contribución en (9) se puede convertir en una integral de superficie usando el teorema de gradiente, corolario del teorema de divergencia (ver Problema 1-15a):

\[\int_{\textrm{V}} \nabla \bigg( \frac{\mu_{0}}{2} \textbf{M} \cdot \textbf{M} \bigg) d \textrm{V} = \oint_{S} \frac{\mu_{0}}{2} \textbf{M} \cdot \textbf{M} d \textrm{S} \nonumber \]

Dado que esta superficie S rodea al medio magnetizable, se encuentra en una región donde M = 0 de manera que las integrales en (11) son cero. Por esta razón la densidad de fuerza de (9) se escribe como

\[\textbf{F} = \mu_{0} ( \textbf{M} \cdot \nabla) \textbf{H} + \mu_{0} \textbf{J}_{f} \times \textbf{H} \nonumber \]

Es el primer término del lado derecho en (12) que da cuenta de que un objeto de hierro debe ser dibujado hacia un imán. Los materiales magnetizables son atraídos hacia regiones de H superior.

5-8-2 Fuerza en un Bucle de Corriente

a) Sólo Fuerza Lorentz

Dos cables paralelos están conectados entre sí por un cable que es libre de moverse, como se muestra en la Figura 5-27a. Se impone una corriente I y se coloca todo el bucle en un campo magnético uniforme\(B_{0} \textbf{i}_{x}\). La fuerza de Lorentz en el cable móvil es

\[f_{y} = I B_{0} l \nonumber \]

donde descuidamos el campo magnético generado por la corriente, asumiendo que es mucho menor que el campo impuesto\(B_{0}\).

(b) Fuerza de magnetización solamente

El alambre deslizante ahora está rodeado por un cilindro hueco infinitamente permeable de radio interior a y radio exterior b, siendo ambos pequeños en comparación con la longitud l del cable, como en la Figura 5-27b. Para distancias cercanas al cilindro, la solución es aproximadamente la misma que si el cable fuera infinitamente largo. Para r>0 no hay corriente, así el campo magnético está libre de rizo y divergencia dentro de cada medio de manera que el potencial escalar magnético obedece a la ecuación de Laplace como en la Sección 5-7-2. En geometría cilíndrica utilizamos los resultados de la Sección 4-3 e intentamos un potencial escalar de la forma

\[\chi = \bigg( A \textrm{r} + \frac{C}{\textrm{r}} \bigg) \cos \phi \nonumber \]

Figura 5-27 (a) La fuerza Lorentz sobre un cable portador de corriente en un campo magnético. (b) Si el cable portador de corriente está rodeado por un cilindro hueco infinitamente permeable, no hay fuerza Lorentz ya que el campo magnético impuesto es cero donde está la corriente. Sin embargo, la fuerza de magnetización sobre el cilindro es la misma que en (a). (c) La fuerza total sobre un alambre magnéticamente permeable portador de corriente tampoco se modifica.

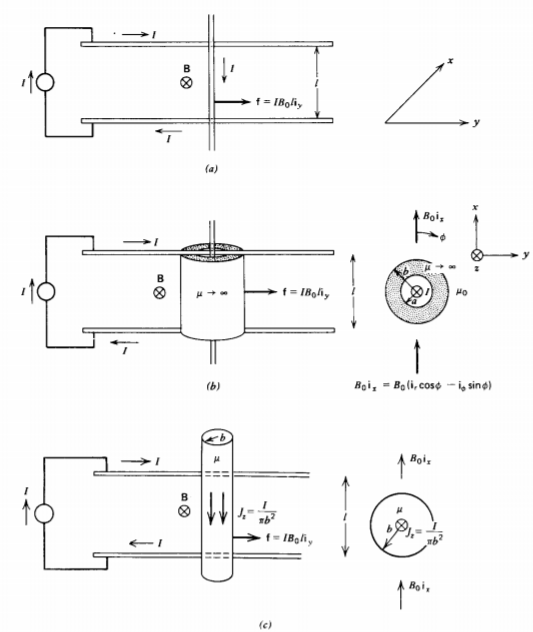
en cada región, donde\(\textbf{B} = \nabla_{\chi}\) porque\(\nabla \times \textbf{B} = 0\). Las constantes se evalúan requiriendo que el campo magnético se aproxime\(B_{0} \textbf{i}_{x}\) al campo impuesto a r =\(\infty\) y sea normalmente incidente sobre el cilindro infinitamente permeable a r = a y r = b. Además, debemos sumar el campo magnético generado por la corriente de línea. El campo magnético en cada región es entonces

(Ver Problema 32a):

\[\textbf{B} = \left \{ \begin{matrix} \frac{\mu_{0}I}{2 \pi \textrm{r}} \textbf{i}_{\phi}, & 0 < \textrm{r} < a \\ \frac{2B_{0}b^{2}}{b^{2}-a^{2}} \bigg[ \bigg( 1 - \frac{a^{2}}{\textrm{r}^{2}} \bigg) \cos \phi \textbf{i}_{\textrm{r}} - \bigg( 1 + \frac{a^{2}}{\textrm{r}^{2}} \bigg) \sin \phi \textbf{i}_{\phi} \bigg] + \frac{\mu I}{2 \pi \textrm{r}} \textbf{i}_{\phi}, & a < \textrm{r} < b \\ B_{0} \bigg[ \bigg( 1 + \frac{b^{2}}{\textrm{r}^{2}} \bigg) \cos \phi \textbf{i}_{\textrm{r}} - \bigg( 1 - \frac{b^{2}}{\textrm{r}^{2}} \bigg) \sin \phi \textbf{i}_{\phi} \bigg] + \frac{\mu_{0} I}{2 \pi \textrm{r}} \textbf{i}_{\phi}, & \textrm{r} > b \end{matrix} \right. \nonumber \]

Observe la densidad de flujo infinito en el hierro (\(\mu \rightarrow \infty\)) debido a la corriente de línea que establece el campo H finito. Sin embargo, vemos que ninguno del campo magnético impuesto es incidente sobre el cable portador de corriente porque está blindado por la cubierta cilíndrica infinitamente permeable de manera que la contribución de la fuerza de Lorentz en el alambre es cero. Hay, sin embargo, una fuerza de magnetización en la carcasa cilíndrica donde el campo magnético interno H se debe enteramente a la corriente de línea\(\mu \rightarrow \infty\),\(H_{\phi} = I/2 \pi\) r porque con, la contribución debida a\(B_{0}\) es insignificante:

\[\textbf{F} = \mu_{0} (\textbf{M} \cdot \nabla) \textbf{H} \\ = \mu_{0} \bigg( M_{\textrm{r}} \frac{\partial}{\partial \textrm{r}} (H_{\phi} \textbf{i}_{\phi}) + \frac{M_{\phi}}{\textrm{r}} \frac{\partial}{\partial \phi} (H_{\phi} \textbf{i}_{\phi}) \bigg) \nonumber \]

Dentro de la carcasa infinitamente permeable, los campos de magnetización y H son

\[H_{\phi} = \frac{I}{2 \pi r} \\ \mu_{0} M_{\textrm{r}} = B_{\textrm{r}} - \mu_{0} H \nearrow^{0}_{\textrm{r}} = \frac{2 B_{0}b^{2}}{b^{2} - a^{2}} \bigg( 1 - \frac{a^{2}}{\textrm{r}^{2}} \bigg) \cos \phi \\ \mu_{0} M_{\phi} = B_{\phi} - \mu_{0} H_{\phi} = - \frac{2 B_{0}b^{2}}{(b^{2}-a^{2})} \bigg( 1 + \frac{a^{2}}{\textrm{r}^{2}} \bigg) \sin \phi + \frac{(\mu - \mu_{0})I}{2 \pi \textrm{r}} \nonumber \]

Aunque\(H_{\phi}\) solo depende de r, el vector unitario\(\textbf{i}_{phi}\) depende de\(\phi\).

\[\textbf{i}_{\phi} = (-\sin \phi \textbf{i}_{x} + \cos \phi \textbf{i}_{y}) \nonumber \]

de manera que la densidad de fuerza de (16) se convierte

\[\textbf{F} = - \frac{B_{\textrm{r}}I}{2 \pi \textrm{r}^{2}} \textbf{i}_{\phi} + \frac{(B_{\phi} - \mu_{0} H_{\phi})I}{2 \pi \textrm{r}^{2}} \frac{d}{d \phi} (\textbf{i}_{\phi}) \\ \frac{I}{2 \pi textrm{r}^{2}} [ - B_{\textrm{r}} (- \sin \phi \textbf{i}_{x} + \cos \phi \textbf{i}_{y}) \\ + (B_{\phi} - \mu_{0} H_{\phi})(- \cos \phi \textbf{i}_{x} - \sin \phi \textbf{i}_{y})] \\ = \frac{I}{2 \pi \textrm{r}^{2}} \bigg( - \frac{2 B_{0} b^{2}}{b^{2}-a^{2}} \bigg[ \bigg( 1 - \frac{a^{2}}{\textrm{r}^{2}} \bigg) \cos \phi (- \sin \phi \textbf{i}_{x} + \cos \phi \textbf{i}_{y}) \\ - \bigg( 1 + \frac{a^{2}}{\textrm{r}^{2}} \bigg) \sin \phi (\cos \phi \textbf{i}_{x} + \sin \phi \textbf{i}_{y}) \bigg] \\ + \frac{(\mu - \mu_{0}) I}{2 \pi \textrm{r}} (\cos \phi \textbf{i}_{x} + \sin \phi \textbf{i}_{y}) \bigg) \\ = \frac{I}{2 \pi \textrm{r}^{2}} \bigg[ - \frac{2 B_{0} b^{2}}{b^{2} - a^{2}} \bigg( -2 \sin \phi \cos \phi \textbf{i}_{x} - \frac{2a^{2}}{\textrm{r}^{2}} \textbf{i}_{y} \bigg) + \frac{(\mu - \mu_{0})I}{2 \pi \textrm{r}} (\cos \phi \textbf{i}_{x} + \sin \phi \textbf{i}_{y}) \bigg) \nonumber \]

La fuerza total sobre el cilindro se obtiene integrando (19) sobre r y\(\phi\).

\[\textbf{f} = \int_{\phi = 0}^{2\pi} \int_{\textrm{r} = a}^{b} \textbf{F} l \: \textrm{r} \: d \textrm{r} \: d \phi \nonumber \]

Todos los términos trigonométricos en (19) se integran a cero sobre para\(\phi\) que la fuerza total sea

\[f_{y} = \frac{2 B_{0} b^{2} I l}{(b^{2} - a^{2}) \int_{\textrm{r} = a}}^{b} \frac{a^{2}}{\textrm{r}^{3}} d \textrm{r} \\ = - \frac{B_{0}b^{2} I l}{(b^{2} - a^{2})} \frac{a^{2}}{\textrm{r}^{2}} \bigg|_{a}^{b} \\ = I B_{0} l \nonumber \]

La fuerza sobre el cilindro es la misma que la de un cable portador de corriente sin blindaje dada por (13). Si el núcleo de hierro tiene una permeabilidad finita, la fuerza total sobre el alambre (fuerza Lorentz) y sobre el cilindro (fuerza de magnetización) vuelve a ser igual a (13). Este hecho se utiliza en maquinaria giratoria donde los alambres portadores de corriente se colocan en ranuras rodeadas de material de hierro altamente permeable. La mayor parte de la fuerza en todo el conjunto está en la plancha y no en el alambre, por lo que es necesaria muy poca fuerza de restricción para mantener el cable en su lugar. La fuerza sobre un cable portador de corriente rodeado de hierro a menudo se calcula usando solo la fuerza de Lorentz, descuidando la presencia del hierro. Se obtiene la respuesta correcta pero por las razones equivocadas. En realidad hay muy poco campo B cerca del alambre ya que está casi rodeado por el hierro de alta permeabilidad por lo que la fuerza Lorentz sobre el alambre es muy pequeña. La fuerza está en realidad sobre el núcleo de hierro.

c) Lorentz y fuerzas de magnetización

Si el cable en sí es altamente permeable con una corriente uniformemente distribuida, como en la Figura 5-27c, el campo magnético es (ver Problema 32a)

\[\textbf{H} = \left \{ \begin{matrix} \frac{2 B_{0}}{\mu + \mu_{0}} (\textbf{i}_{\textrm{r}} \cos \phi - \textbf{i}_{\phi} \sin \theta) + \frac{I \textrm{r}}{2 \pi b^{2}} \textbf{i}_{\phi} & \: \\ = \frac{2B_{0}}{\mu + \mu_{0}} \textbf{i}_{x} + \frac{I}{2 \pi b^{2}} (-y \textbf{i}_{x} + x \textbf{i}_{y}), & \textrm{r} < b \\ \frac{B_{0}}{\mu_{0}} \bigg[ \bigg( 1 + \frac{b^{2}}{\textrm{r}^{2}} \frac{\mu - \mu_{0}}{\mu + \mu_{0}} \bigg) \cos \phi \textbf{i}_{\textrm{r}} & \: \\ - \bigg( 1 - \frac{b^{2}}{\textrm{r}^{2}} \frac{\mu - \mu_{0}}{\mu + \mu_{0}} \bigg) \sin \phi \textbf{i}_{\phi} \bigg] + \frac{I}{2 \pi \textrm{r}} \textbf{i}_{\phi}, & \textrm{r} > b \end{matrix} \right. \nonumber \]

Es conveniente escribir los campos dentro del cilindro en coordenadas cartesianas usando (18) ya que entonces la densidad de fuerza dada por (12) es

\[\textbf{F} = \mu_{0}(\textbf{M} \cdot \nabla) \textbf{H} + \mu_{0} \textbf{J}_{f} \times \textbf{H} \\ = (\mu - \mu_{0}) (\textbf{H} \cdot \nabla) \textbf{H} + \frac{\mu_{0} I}{\pi b^{2}} \textbf{i}_{z} \times \textbf{H} \\ = (\mu - \mu_{0}) (\textbf{H} \cdot \nabla) \textbf{H} + \frac{\mu_{0} I}{\pi b^{2}} \textbf{i}_{z} \times \textbf{H} \\ = (\mu - \mu_{0}) \bigg( H_{x} \frac{\partial}{\partial x} + H_{y} \frac{\partial}{\partial y} \bigg) (H_{x} \textbf{i}_{x} + H_{y} \textbf{i}_{y}) + \frac{\mu_{0}I}{\pi b^{2}} (H_{x} \textbf{i}_{y} - H_{y} \textbf{i}_{x}) \nonumber \]

Dado que dentro del cilindro (r < b) las derivadas parciales de H son

\[\frac{\partial H_{x}}{\partial x} = \frac{\partial H_{y}}{\partial y} = 0 \\ \frac{\partial H_{x}}{\partial y} = - \frac{\partial H_{y}}{\partial x} = - \frac{I}{2 \pi b^{2}} \nonumber \]

(23) reduce a

\[\textbf{F} = (\mu - \mu_{0}) \bigg( H_{x} \frac{\partial H_{y}}{\partial x} \textbf{i}_{y} + H_{y} \frac{\partial H_{x}}{\partial y} \textbf{i}_{x} \bigg) + \frac{\mu_{0}I}{\pi b^{2}} (H_{x} \textbf{i}_{y} - H_{y} \textbf{i}_{x}) \\ = \frac{I}{2 \pi b^{2}} (\mu + \mu_{0}) (H_{x} \textbf{i}_{y} - H_{y} \textbf{i}_{x}) \\ = \frac{I (\mu + \mu_{0})}{2 \pi b^{2}} \bigg[ \bigg( \frac{2 B_{0}}{\mu + \mu_{0}} - \frac{Iy}{2 \pi b^{2}} \bigg) \textbf{i}_{y} - \frac{Ix}{2 \pi b^{2}} \textbf{i}_{x} \bigg] \nonumber \]

Darse cuenta de la Tabla 1-2 que

\[y \textbf{i}_{y} + x \textbf{i}_{x} = \textrm{r} [ \sin \phi \textbf{i}_{y} + \cos \phi \textbf{i}_{x}] = \textrm{r} \textbf{i}_{\textrm{r}} \nonumber \]

la densidad de fuerza se puede escribir como

\[\textbf{F} = \frac{IB_{0}}{\pi b^{2}} \textbf{i}_{y} - \frac{I^{2} (\mu + \mu_{0})}{(2 \pi b^{2})^{2}} \textrm{r} (\sin \phi \textbf{i}_{y} + \cos \phi \textbf{i}_{x}) \nonumber \]

La fuerza total sobre el alambre permeable es

\[\textbf{f} = \int_{\phi = 0}^{2 \pi} \int_{\textrm{r} = 0}^{b} \textbf{F} l r d \textrm{r} \: d \phi \nonumber \]

Vemos que los términos trigonométricos en (27) se integran a cero para que solo el primer término contribuya:

\[f_{y} = \frac{I B_{0} l}{\pi b^{2}} \int_{\phi = 0}^{2 \pi} \int_{\textrm{r = 0}}^{b} \textrm{r} \: d \textrm{r} \: d \phi \\ = I B_{0} l \nonumber \]

La fuerza total sobre el alambre es independiente de su permeabilidad magnética.