6.1: Ley de Inducción de Faraday
- Page ID
- 86759
6-1-1 La fuerza electromotriz (CEM)
Los experimentos originales de Faraday consistieron en un bucle conductor a través del cual podía imponer una corriente continua a través de un interruptor. Otro bucle cortocircuitado sin fuente conectada estaba cerca, como se muestra en la Figura 6-1. Cuando una corriente continua fluyó en el bucle 1, no fluyó corriente en el bucle 2. Sin embargo, cuando el voltaje se aplicó por primera vez al bucle 1 cerrando el interruptor, una corriente transitoria fluyó en dirección opuesta en el bucle 2.
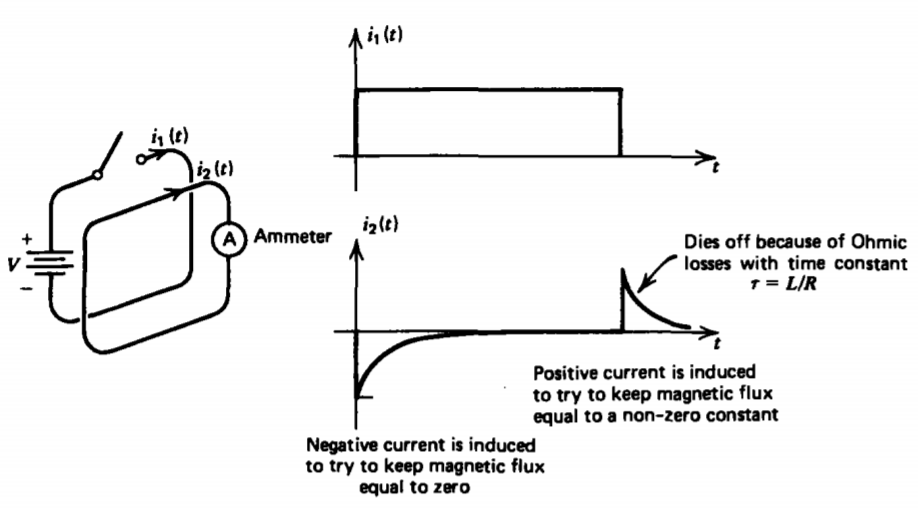
Cuando posteriormente se abrió el interruptor, otra corriente transitoria fluyó en el bucle 2, esta vez en la misma dirección que la corriente original en el bucle 1. Las corrientes se inducen en el bucle 2 siempre que un flujo magnético variable en el tiempo debido al bucle 1 pasa a través de él.
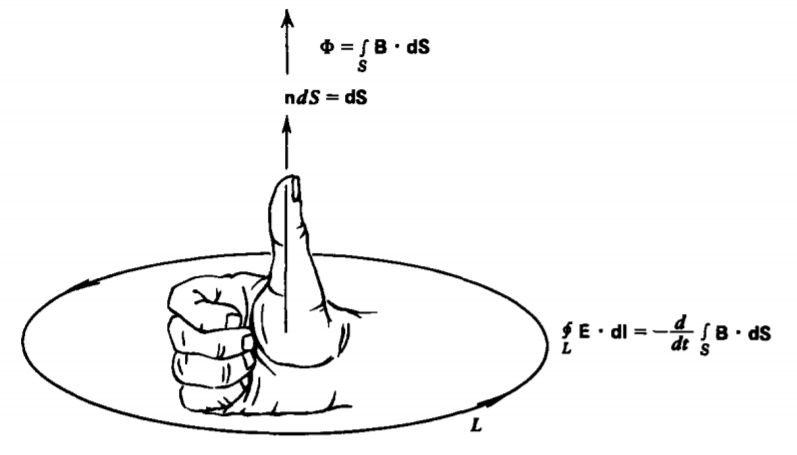
En general, un flujo magnético variable en el tiempo puede pasar a través de un circuito debido a su propia corriente variable en el tiempo o cercana o por el movimiento del circuito a través de un campo magnético. Para cualquier bucle, como en la Figura 6-2, la ley de Faraday es
\[\textrm{EMF} = \oint_{L} \textbf{E} \cdot \textbf{dl} = - \frac{d \Phi}{dt} = - \frac{d}{dt} \int_{S} \textbf{B} \cdot \textbf{dS} \nonumber \]
donde EMF es la fuerza electromotriz definida como la línea integral del campo eléctrico. El signo menos se introduce en el lado derecho de (1) a medida que tomamos la convención de que el flujo positivo fluye en la dirección perpendicular a la dirección del contorno por la regla de la derecha.
6-1-2 Ley de Lenz
La dirección de las corrientes inducidas es siempre tal que se opone a cualquier cambio en el flujo magnético ya presente. Así, en el experimento de Faraday, ilustrado en la Figura 6-1, cuando el interruptor en el bucle 1 se cierra por primera vez no hay flujo magnético en el bucle 2 de manera que la corriente inducida fluye en dirección opuesta con su campo automagnético opuesto al campo impuesto. La corriente inducida intenta mantener un flujo cero a través de
bucle 2. Si el bucle es perfectamente conductor, la corriente inducida fluye siempre que la corriente fluya en el bucle 1, con flujo neto cero a través del bucle. Sin embargo, en un bucle real, las pérdidas resistivas hacen que la corriente disminuya exponencialmente con una constante de tiempo L/R, donde L es la autoinductancia del bucle y R es su resistencia. Así, en el estado estacionario dc la corriente inducida ha decaído a cero de manera que un flujo magnético constante pasa a través del bucle 2 debido a la corriente en el bucle 1.
Cuando el interruptor se abre posteriormente para que la corriente en el bucle 1 vaya a cero, el segundo bucle intenta mantener el flujo constante ya presente induciendo un flujo de corriente en la misma dirección que la corriente original en el bucle 1. Las pérdidas óhmicas vuelven a hacer que esta corriente inducida muera con el tiempo.
Si se hace que un circuito o cualquier parte de un circuito se mueva a través de un campo magnético, se inducirán corrientes en la dirección tal como para tratar de mantener constante el flujo magnético a través del bucle. La fuerza sobre la corriente en movimiento siempre será opuesta a la dirección del movimiento.
La ley de Lenz queda claramente demostrada por los experimentos mostrados en la Figura 6-3. Cuando un hacha conductora se mueve hacia un campo magnético, las corrientes parásitas se inducen en la dirección en la que su flujo automático es opuesto al campo magnético aplicado. La fuerza Lorentz se encuentra entonces en la dirección opuesta al movimiento del hacha. Esta fuerza disminuye con el tiempo ya que las corrientes disminuyen con el tiempo debido a la disipación óhmica. Si el hacha fue ranurado, creando efectivamente una resistencia muy alta a las corrientes parásitas, la fuerza de reacción se vuelve muy pequeña ya que la corriente inducida es pequeña.
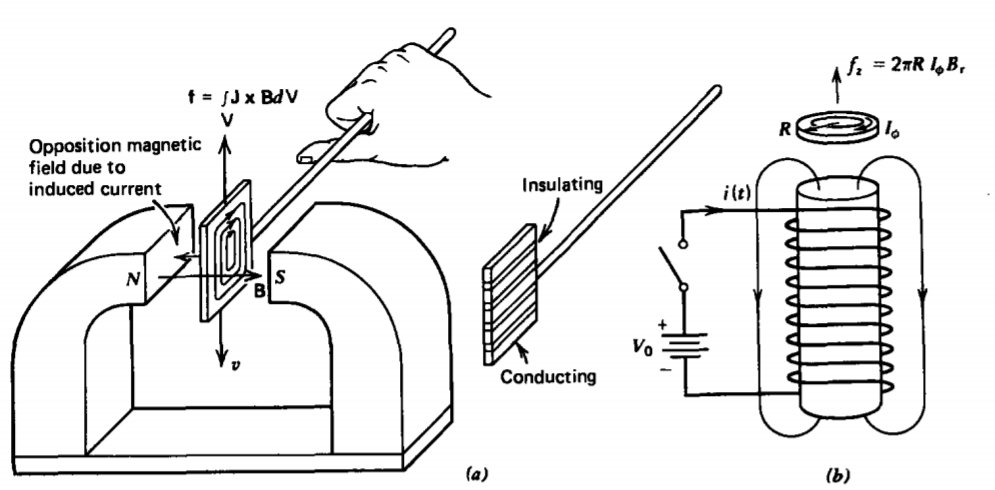
\[\textbf{f} = 2 \pi R \textbf{I} \times \textbf{B} = 2 \pi RI_{\phi} B_{\textrm{r} \textbf{i}_{z} \nonumber \]
que voltea el anillo de la bobina. Si el anillo se corta radialmente para que no pueda fluir ninguna corriente circulante, la fuerza es cero y el anillo no se mueve
(a) Bucle cortocircuitado
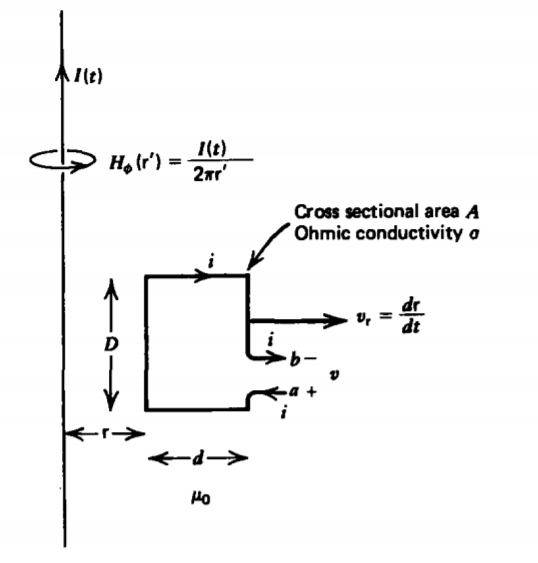
Para ser cuantitativo, considere la corriente de línea variable en el tiempo infinitamente largo I (t) en la Figura 6-4, una distancia r de un bucle rectangular de alambre con conductividad óhmica\(\sigma\), área de sección transversal A y longitud total\(l = 2(D + d)\). El flujo magnético a través del bucle debido a I (t) es
\[\Phi_{m} = \int_{z= -D/2}^{D/2} \int_{\textrm{r}}^{\textrm{r} + d} \mu_{0} H_{\phi}(\textrm{r}') d \textrm{r}' dz \\ = \frac{\mu_{0}ID}{2 \pi} \int_{\textrm{r}}^{\textrm{r} + d} \frac{d \textrm{r}'}{\textrm{r}'} = \frac{\mu_{0} ID}{2 \pi} \ln \frac{\textrm{r} + d}{\textrm{r}} \nonumber \]
La inductancia mutua M se define como la relación de flujo a corriente donde el flujo a través del bucle se debe a una corriente externa. Entonces (3) se convierte en
\[\Phi_{m} = M(\textrm{r})I, \: \: \: \: M(\textrm{r}) = \frac{\mu_{0}D}{2 \pi} \ln \frac{\textrm{r} + d}{\textrm{r}} \nonumber \]
Cuando el bucle es cortocircuitado (\(v\)= 0), la corriente óhmica inducida\(i\) da lugar a un campo eléctrico [\(E = J/\sigma = i/ (A \sigma)\)] de manera que la ley de Faraday aplicada a un contorno dentro del cable produce una fuerza electromotriz igual a la caída de tensión óhmica:
\[\oint_{L} \textbf{E} \cdot \textbf{dl} = \frac{il}{\sigma A} = iR = - \frac{d \Phi}{dt} \nonumber \]
donde\(R = L/(\sigma A)\) esta la resistencia, del bucle. Por convención, la corriente se toma como positiva en la dirección de la línea integral.
El flujo en (5) tiene contribuciones tanto de la corriente impuesta como se da en (3) como de la corriente inducida proporcional a la autoinductancia L del bucle, que por ejemplo se da en la Sección 5-4-3c para un bucle cuadrado (D = d):
\[\Phi = M(\textrm{r}) I + Li \nonumber \]
Si el bucle también se mueve radialmente hacia afuera con la velocidad\(v_{\textrm{r}} = d \textrm{r} /dt\), el voltaje óhmico inducido electromotivamente es
\[-iR = \frac{d \Phi}{dt} \\ = M(\textrm{r}) \frac{dI}{dt} + I \frac{dM(\textrm{r})}{dt} + L \frac{di}{dt} \\ = M(\textrm{r}) \frac{dI}{dt} + I \frac{dM}{d \textrm{r}} \frac{d \textrm{r}}{dt} + L \frac{di}{dt} \nonumber \]
donde L no es una función de la posición radial del bucle.
Si el bucle es estacionario, solo contribuyen los términos primero y tercero del lado derecho. Son distintos de cero sólo si las corrientes cambian con el tiempo. El segundo término se debe al movimiento y tiene un aporte incluso para corrientes dc.
Encendido Transitorio. Si el bucle es estacionario (\(d \textrm{r}/dt = 0\)) a r = r 0, (7) se reduce a
\[L \frac{di}{dt} + iR = - M(\textrm{r}_{0}) \frac{dI}{dt} \nonumber \]
Si la corriente aplicada I es un paso dc encendido a t = 0, la solución a (8) es
\[i(t) = 0 \frac{M(\textrm{r}_{0})I}{L} e^{-(R/L)t}, \: \: \: t > 0 \nonumber \]
donde el término de impulso en el lado derecho de (8) impone la condición inicial\(i(t = 0) = -M(\textrm{r}_{0})I/L\). La corriente es negativa, ya que la ley de Lenz requiere que el flujo propio se oponga al flujo aplicado.
Transitorio de apagado. Si después de mucho tiempo T la corriente I se apaga instantáneamente, la solución es
\[i(t) = \frac{M(\textrm{r}_{0})I}{L} e^{-(R/L)(t-T)}, \: \: \: t > T \nonumber \]
donde ahora la disminución escalonada en la corriente I a t = T invierte la dirección de la corriente inicial.
Movimiento con corriente continua. Con una corriente continua, el primer término en el lado derecho en (7) es de rendimiento cero
\[L \frac{di}{dt} + iR = \frac{\mu_{0}IDd}{2 \pi \textrm{r}(\textrm{r} + d)} \frac{d \textrm{r}}{dt} \nonumber \]
Para continuar, debemos especificar la moción para que sepamos cómo cambia r con el tiempo. Consideremos el caso más simple cuando el bucle no tiene resistencia (R = 0). Entonces (11) se puede integrar directamente a
\[Li = - \frac{\mu_{0}ID}{2 \pi} \ln \frac{1 + d/ \textrm{r}}{1 + d/ \textrm{r}_{0}} \nonumber \]
donde especificamos que la corriente es cero cuando r =ro. Esta solución para un bucle sin pérdidas solo requiere que el flujo total de (6) permanezca constante. La corriente es positiva cuando r> r 0 ya que el autoflujo debe ayudar al flujo decreciente impuesto. La corriente es igualmente negativa cuando r < r 0 ya que el autoflujo debe cancelar el flujo impuesto creciente.
La fuerza en el bucle para todos estos casos solo se debe a la fuerza en las patas de corriente dirigida z en r y r+ d:
\[f_{\textrm{r}} = \frac{\mu_{0}DiI}{2 \pi} \bigg( \frac{1}{\textrm{r} + d} - \frac{1}{\textrm{r}}\bigg) \\ = - \frac{\mu_{0}DiId}{2 \pi \textrm{r}(\textrm{r} + d)} \nonumber \]
siendo atractivo si ii > 0 y repulsivo si iL <0.
(b) Circuito abierto
Si el bucle es de circuito abierto, no puede fluir corriente inducida y por lo tanto el campo eléctrico dentro del cable es cero (\(\textbf{J} = \sigma \textbf{E} = 0\)). La fuerza electromotriz entonces solo tiene una contribución del espacio entre terminales igual al negativo de la tensión:
\[\oint_{L} \textbf{E} \cdot \textbf{dl} = \int_{b}^{a} \textbf{E} \cdot \textbf{dl} = - v = - \frac{d \Phi}{dt} \Rightarrow v = \frac{d \Phi}{dt} \nonumber \]
Tenga en cuenta en la Figura 6-4 que nuestra convención es tal que la corriente i siempre se define positiva que fluye fuera del terminal de voltaje positivo hacia el bucle. El flujo\(\Phi\) en (14) ahora solo se debe al flujo mutuo dado por (3), ya que con i =0 no hay auto-flujo. El voltaje en el circuito abierto en movimiento es entonces
\[v = M (\textrm{r}) \frac{dI}{dt} + I \frac{dM}{d \textrm{r}} \frac{d \textrm{r}}{dt} \nonumber \]
c) Fuerza de reacción
La fuerza magnética en un bucle móvil cortocircuitado está siempre en la dirección opuesta a su movimiento. Considere el bucle cortocircuitado en la Figura 6-5, donde un lado del bucle se mueve con velocidad\(v_{x}\). Con un campo magnético uniforme aplicado normal al bucle que señala fuera de la página, una expansión del bucle tiende a vincular más flujo magnético requiriendo que la corriente inducida fluya en sentido horario para que su auto-flujo esté en la dirección dada por la regla de la derecha, opuesta al campo aplicado. Desde (1) tenemos
\[\oint_{L} \textbf{E} \cdot \textbf{dl} = \frac{il}{\sigma A} = iR = - \frac{d \Phi}{dt} = B_{0}D \frac{dx}{dt} = B_{0}Dv_{x} \nonumber \]
donde\(l = 2 (D + x)\) también cambia con el tiempo. La corriente es entonces
\[i = \fracc{B_{0}Dv_{x}}{R} \nonumber \]
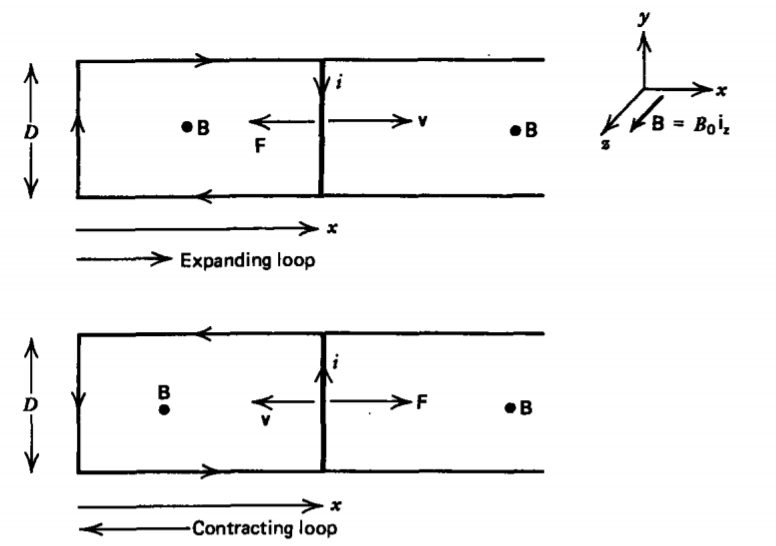
donde descuidamos el autoflujo generado por\(i\), asumiendo que es mucho menor que el flujo aplicado debido a\(B_{0}\). Tenga en cuenta también que el flujo aplicado es negativo, ya que la regla de la derecha aplicada a la dirección de la corriente define el flujo positivo hacia la página, mientras que el flujo aplicado apunta hacia afuera.
La fuerza en el lado móvil está entonces a la izquierda,
\[\textbf{f} = -iD \textbf{i}_{y} \times B_{0} \textbf{i}_{z} = iD B_{0} \textbf{i}_{x} = - \frac{B_{0}^{2}D^{2}v_{x}}{R} \textbf{i}_{x} \nonumber \]
opuesto a la velocidad.
Sin embargo, si el lado se mueve hacia la izquierda (\(v_{x}\)<0), disminuyendo el área del bucle, vinculando así menos flujo, la corriente invierte la dirección al igual que la fuerza.
6-1-3 Laminaciones
Las corrientes parásitas inducidas en conductores óhmicos resultan en calentamiento óhmico. Esto es útil en hornos de inducción que funden metales, pero no es deseado en muchos dispositivos con núcleo de hierro. Para reducir esta pérdida de energía, los núcleos a menudo se cortan en muchas láminas delgadas aisladas eléctricamente entre sí por recubrimientos finos de óxido. El flujo de corriente se limita entonces para que se encuentre dentro de una lámina delgada y no pueda cruzarse entre láminas. Las laminaciones aislantes sirven para el mismo propósito que los cortes en el hacha ranurada en la Figura 6-3a.
El conductor rectangular en la Figura 6-6a tiene un campo magnético variable en el tiempo B (t) que pasa a través de él. Aproximamos la trayectoria actual siguiendo la forma rectangular para que
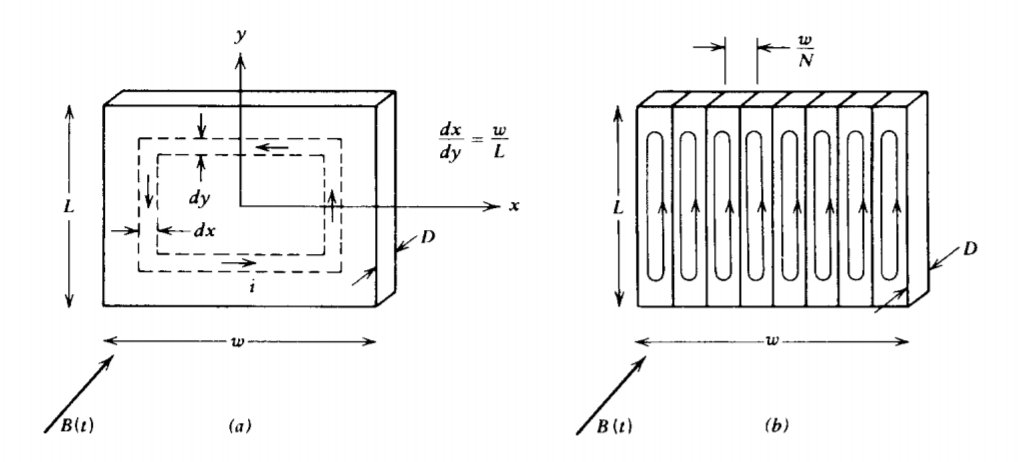
el flujo a través del bucle de ancho incremental dx y dy del área 4 xy es
\[\Phi = - 4 xy B (t) \nonumber \]
donde descuidamos el campo de reacción de la corriente inducida asumiendo que es mucho menor que el campo impuesto. El signo menos surge porque, por la regla de la derecha ilustrada en la Figura 6-2, el flujo positivo fluye en dirección opuesta a B (t). La resistencia del bucle es
\[R_{x} = \frac{4}{\sigma D} \bigg( \frac{y}{dx} + \frac{x}{dy} \bigg) = \frac{4}{\sigma D} \frac{L}{w} \frac{x}{dx} \bigg[ 1 + \bigg( \frac{w}{L} \bigg)^{2} \bigg] \nonumber \]
La fuerza electromotriz alrededor del bucle entonces solo resulta en una corriente óhmica:
\[\oint_{L} \textbf{E} \cdot \textbf{dl} = i R_{x} = \frac{-d \Phi}{dt} = 4xy \frac{dB}{dt} = \frac{4L}{w} x^{2} \frac{dB}{dt} \nonumber \]
con potencia disipada
\[dp = i^{2} R_{x} = \frac{4 Dx^{3} \sigma L (dB/dt)^{2}dx}{w[1 + (w/L)^{2}]} \nonumber \]
La potencia total disipada sobre toda la hoja se encuentra luego agregando las potencias disipadas en cada bucle incremental:
\[P = \int_{0}^{w/2} dp \\ = \frac{4D (dB/dt)^{2}\sigma L}{wp1 + (w/L)^{2}]} \int_{0}^{w/2} x^{3}dx \\ = \frac{LDw^{3} \sigma (dB/dt)^{2}}{16[1 _ w/L)^{2}]} \nonumber \]
Si la lámina se lamina en N menores, como en la Figura 6-6b, cada sección tiene la misma solución que (23) si reemplazamos w por WiN. La potencia total disipada es entonces N veces la potencia disipada en una sola sección:
\[P = \frac{LD (w/N)^{3} \sigma (dB/dt)^{2}N}{16[1 + (w/NL)^{2}]} = \frac{\sigma L D w^{3} (dB/dt)^{2}}{16 N^{2}[1 + (w/NL)^{2}]} \nonumber \]
A medida que N se vuelve grande de manera que\(w/NL <<1\), la potencia disipada disminuye como 1/ N 2.
6-1-4 Betatrón
El ciclotrón, discutido en la Sección 5-1-4, no se utiliza para acelerar electrones porque su pequeña masa les permite alcanzar velocidades relativistas, incrementando así su masa y disminuyendo su velocidad angular. Esto los pone fuera de fase con el voltaje aplicado. El betatrón de la Figura 6-7 utiliza el principio del transformador donde los electrones que circulan alrededor del toroide evacuado actúan como un devanado secundario. El flujo magnético impuesto que varía en el tiempo genera un campo eléctrico que acelera los electrones.
La ley de Faraday se aplicó a un contorno siguiendo la trayectoria de la carga en el radio R rendimientos
\[\oint_{L} \textbf{E} \cdot \textbf{dl} = E_{\phi} 2 \piR = - \frac{d \Phi}{dt} \nonumber \]
que acelera los electrones como
\[m \frac{dv_{\phi}}{dt} = - eE_{\phi} = \frac{e}{2 \pi R} \frac{d \Phi}{dt} \Rightarrow v_{\phi} = \frac{e}{2 \pi m R} \Phi \nonumber \]
Los electrones se mueven en la dirección de manera que su flujo automagnético es opuesto al flujo aplicado. La fuerza resultante de Lorentz es radialmente hacia adentro. Se logra una órbita estable de radio constante R si esta fuerza equilibra la fuerza centrífuga:
\[m \frac{dv_{r}}{dt} = \frac{mv^{2}_{\phi}}{R} - ev_{\phi}B_{z}(R) = 0 \nonumber \]
que de (26) requiere que el flujo y el campo magnético se relacionen como
\[\Phi = 2 \pi R^{2} B_{z} (R) \nonumber \]
Esta condición no puede ser satisfecha por un campo uniforme (como entonces\(\Phi = \pi R^{2} B_{z}\)) por lo que en la práctica el campo impuesto se hace variar aproximadamente con la posición radial como
\[B_{z}(r) = B_{0} \bigg( \frac{R}{r} \bigg) \Rightarrow \Phi = 2 \pi \int_{r = 0}^{R} B_{z} (r)r \: dr = 2 \pi R^{2} B_{0} \nonumber \]
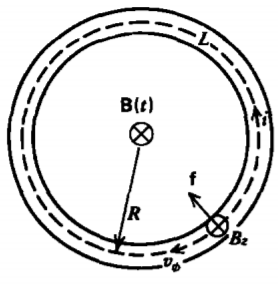
donde R es el radio de órbita de equilibrio, de manera que (28) se satisface.
El campo magnético debe permanecer libre de rizos donde no haya corriente, de modo que la variación espacial en (29) requiera un componente de campo magnético radial:
\[\nabla \times \textbf{B} = \bigg( \frac{\partial B_{r}}{\partial z} - \frac{\partial B_{z}}{\partial r} \bigg) \textbf{i}_{\phi} = 0 \Rightarrow B_{r} = - \frac{B_{0}R}{r^{2}} z \nonumber \]
Luego cualquier desplazamiento de perturbación dirigido por z
\[\frac{d^{2}z}{dt^{2}} = \frac{ev_{\phi}}{m} B_{r}(R) = - \bigg( \frac{eB_{0}}{m} \bigg)^{2} z \\ \Rightarrow z = A_{1} \sin \omega_{0} t + A_{2} \cos \omega_{0} t, \: \: \: \: \omega_{0} = \frac{eB_{0}}{m} \nonumber \]
tienen soluciones sinusoidales a la frecuencia de ciclotrón\(\omega_{0} = eB_{0}/m\), conocidas como oscilaciones de betatrón.
6-1-5 Ley de Faraday y Teorema de Stokes
La forma integral de la ley de Faraday en (1) muestra que con la inducción magnética el campo eléctrico ya no es conservador ya que su línea integral alrededor de un camino cerrado no es cero. Podemos convertir (1) a su forma diferencial equivalente considerando un contorno estacionario cuya forma no varía con el tiempo. Debido a que el área para la integral de superficie no cambia con el tiempo, la derivada del tiempo en el lado derecho en (1) puede llevarse dentro de la integral pero se convierte en una derivada parcial porque B también es una función de la posición:
\[\oint_{L} \textbf{E} \cdot \textbf{dl} = - \int_{S} \frac{\partial \textbf{B}}{\partial t} \cdot \textbf{dS} \nonumber \]
Usando el teorema de Stokes, el lado izquierdo de (32) se puede convertir en una integral de superficie,
\[\oint_{L} \textbf{E} \cdot \textbf{dl} = \int_{S} \nabla \times \textbf{E} \cdot \textbf{dS} = - \int_{S} \frac{\partial \textbf{B}}{\partial t} \cdot \textbf{dS} \nonumber \]
que es equivalente a
\[\int_{S} \bigg( \nabla \times \textbf{E} + \frac{\partial \textbf{B}}{\partial t} \bigg) \textbf{dS} = 0 \nonumber \]
Como esta última relación es cierta para cualquier superficie, el integrando en sí debe ser cero, lo que arroja la ley de inducción de Faraday en forma diferencial como
\[\nabla \times \textbf{E} = - \frac{\partial \textbf{B}}{\partial t} \nonumber \]


