6.3: Energía almacenada en el campo magnético
- Page ID
- 86750
6-3-1 La transformación del campo eléctrico
Si una carga puntual q viaja con una velocidad v a través de una región con campo eléctrico E y campo magnético B, experimenta la fuerza combinada de Coulomb-Lorentz
\[\textbf{F} = q (\textbf{E} + \textbf{v} \times \textbf{B}) \nonumber \]
Consideremos ahora otro observador que está viajando a la misma velocidad v que el portador de carga para que su velocidad relativa sea cero. Este observador en movimiento dirá entonces que no hay fuerza Lorentz, solo una fuerza coulómbica
\[\textbf{F}' = q \textbf{E}' \nonumber \]
donde indicamos cantidades medidas por el observador en movimiento con un primo. Un postulado fundamental de la mecánica es que todas las leyes físicas son iguales en cada sistema de coordenadas inerciales (sistemas que viajan a velocidad relativa constante). Esto requiere que la fuerza medida por dos observadores inerciales sea la misma de manera que F '= F:
\[\textbf{E}' = \textbf{E} + \textbf{v} \times \textbf{B} \nonumber \]
El campo eléctrico medido por los dos observadores en movimiento relativo será diferente. Este resultado es correcto para velocidades materiales mucho menores que la velocidad de la luz y se llama transformación de campo galileo. La completa transformación relativisticamente correcta modifica ligeramente (3) y se denomina transformación lorentziana pero no será considerada aquí.
Al usar la ley de Faraday de la Sección 6-1-1, queda la pregunta sobre qué campo eléctrico debe usarse si el contorno L y la superficie S se están moviendo. Se utiliza el campo eléctrico que es medido por un observador que se mueve a la misma velocidad que el contorno de convección. La derivada de tiempo del término de flujo no puede llevarse dentro de la integral si la superficie S es en sí misma una función del tiempo.
Ley de 6-3-2 ohmios para conductores móviles
La transformación del campo eléctrico de (3) es especialmente importante en la modificación de la ley de Ohm para conductores móviles. Para velocidades no relativistas, un observador que se mueve a la misma velocidad que un conductor óhmico mide la ley habitual de Ohm en su marco de referencia,
\[\textbf{J}_{f}' = \sigma \textbf{E}' \nonumber \]
donde asumimos que el proceso de conducción no se ve afectado por el movimiento. Entonces en la relatividad galileana para sistemas sin cargo libre, la densidad de corriente en todos los marcos inerciales es la misma de manera que (3) en (4) nos da la ley generalizada de Ohm como
\[\textbf{J}_{f}' = \textbf{J}_{f} = \sigma (\textbf{E} + \textbf{v} \times \textbf{B}) \nonumber \]
donde v es la velocidad del conductor.
Los efectos del movimiento del material se ilustran mediante la geometría de placa paralela mostrada en la Figura 6-14. Se aplica una fuente de corriente en el lado izquierdo que se distribuye uniformemente como una corriente superficial\(K_{x} = \pm I/D\) en los planos. Los electrodos están conectados por una losa conductora que se mueve hacia la derecha con velocidad constante U. El voltaje a través de la fuente de corriente se puede calcular usando la ley de Faraday con el contorno mostrado. Hagamos que el contorno se expanda continuamente con la pierna 2-3 moviéndose con el conductor. Aplicando la ley de Faraday tenemos
\[\oint_{L} \textbf{E}' \cdot \textbf{dl} = \int_{1}^{2} \textbf{E} \nearrow^{0} \cdot \textbf{dl} + \int_{2}^{3} \underbrace{\textbf{E}' \cdot \textbf{dl}}_{iR} + \int_{3}^{4} \textbf{e} \nearrow^{0} \cdot \textbf{dl} + \int_{4}^{1} \underbrace{\textbf{E} \cdot \textbf{dl}}_{- \nu} \\ = - \frac{d}{dt} \int_{S} \textbf{B} \cdot \textbf{dS} \nonumber \]
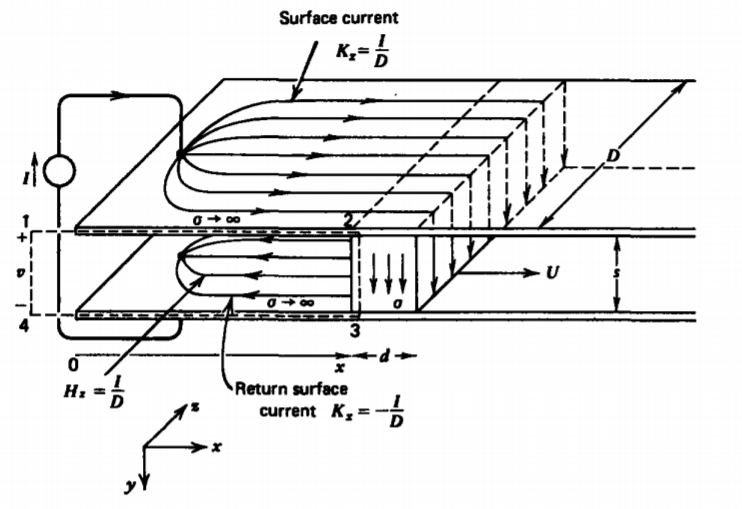
donde el campo eléctrico utilizado a lo largo de cada pata es el medido por un observador en el marco de referencia del contorno. A lo largo de las patas 1-2 y 3-4, el campo eléctrico es cero dentro de los conductores perfectos estacionarios. La segunda integral dentro del conductor óhmico móvil utiliza el campo eléctrico E ', medido por un observador en movimiento porque el contorno también se está expandiendo a la misma velocidad, y desde (4) y (5) se relaciona con la corriente del terminal como
\[\textbf{E}' = \frac{\textbf{J}'}{\sigma} = \frac{I}{\sigma Dd} \textbf{i}_{y} \nonumber \]
En (6), la última línea integral a través de los terminales define el voltaje.
\[\frac{Is}{\sigma Dd} - v = - \frac{d}{dt} \int_{S} \textbf{B} \cdot \textbf{dS} = - \frac{d}{dt} (\mu_{0} H_{z} xs) \nonumber \]
El primer término es solo la caída de voltaje resistiva a través del conductor, presente incluso si no hay movimiento. El término en el lado derecho en (8) solo tiene una contribución debido al aumento lineal del área (\(dx/dt = U\)) en la región del espacio libre con campo magnético constante,
\[H_{z} = I/D \nonumber \]
El voltaje del terminal es entonces
\[ v = I \bigg( R + \frac{\mu_{0}Us}{D} \bigg) , \: \: \: R = \frac{s}{\sigma Dd} \nonumber \]
Vemos que la contribución de voltaje de velocidad surgió del término de flujo en la ley de Faraday. Podemos obtener la misma solución usando un contorno que es estacionario y no se expande con el conductor. Escogemos el contorno para simplemente estar dentro del conductor en el momento de interés. Debido a que el contorno no se expande con el tiempo para que tanto el campo magnético como el área del contorno no cambien con el tiempo, el lado derecho de (6) es cero. La única diferencia ahora es que a lo largo de la pata 2-3 utilizamos el campo eléctrico medido por un observador estacionario,
\[\textbf{E} = \textbf{E}' - \textbf{v} \times \textbf{B} \nonumber \]
de manera que (6) se convierte
\[IR + \frac{\mu_{0} UIs}{D} - v = 0 \nonumber \]
que concuerda con (10) pero con el término de voltaje de velocidad que ahora surge del lado del campo eléctrico de la ley de Faraday.
Esta contribución de voltaje de velocidad es el principio de los generadores eléctricos que convierten el trabajo mecánico en energía eléctrica al mover un conductor portador de corriente a través de un campo magnético. El término de resistencia da cuenta de la energía eléctrica disipada. Tenga en cuenta en (10) que la contribución de voltaje de velocidad solo se suma con la resistencia del conductor para que la resistencia efectiva del terminal sea\(v/I = R + (\mu_{o} Us/D)\). Si la losa se mueve en la dirección opuesta de tal manera que U es negativa, la resistencia terminal también puede llegar a ser negativa para suficientemente grande\(U \: (U < -RD/\mu_{0}s)\). Dichos sistemas son inestables donde los modos naturales crecen en lugar de decaer con el tiempo con cualquier pequeña perturbación, como se ilustra en la Sección 6-3-3b.
6-3-3 Disco de Faraday (Generador Homopolar) *
a) Campo Magnético Impuesto
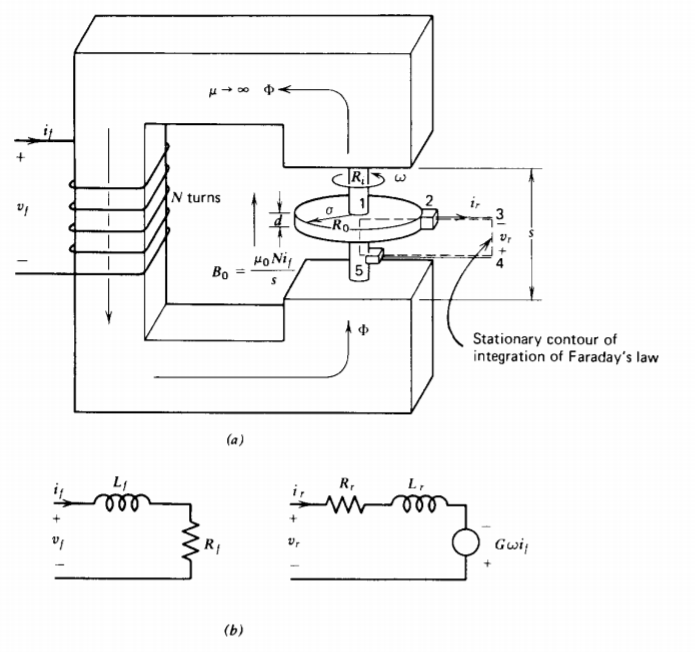
Un disco de conductividad que\(\sigma\) gira a velocidad angular\(\omega\) transversal a un campo magnético uniforme\(B_{0} \textbf{i}_{z}\), ilustra los principios básicos de la conversión de energía electromecánica. En la Figura 6-15a asumimos que el campo magnético es generado por una bobina de N vueltas enrollada en el circuito magnético circundante,
\[B_{0} = \frac{\mu_{0} Ni_{f}}{s} \nonumber \]
El disco y el eje tienen una permeabilidad de espacio libre\(\mu_{0}\), de manera que el campo aplicado no se ve perturbado por el conjunto. El eje y la superficie exterior en r =\(R_{0}\) son altamente conductores y hacen conexión eléctrica a los terminales a través de contactos deslizantes.
Evaluamos la ley de Faraday utilizando el contorno mostrado en la Figura 6-15a donde la pata 1-2 dentro del disco es estacionaria por lo que el campo eléctrico apropiado a utilizar viene dado por (11):
\[E_{\textrm{r}} = \frac{J_{\textrm{r}}}{\sigma} - \omega \textrm{r} B_{0} = \frac{i_{r}}{2 \pi \sigma d \textrm{r}} - \omega \textrm{r} B_{0} \nonumber \]
donde el campo eléctrico y la densidad de corriente son radiales e i, es la corriente total del terminal del rotor. Para el contorno estacionario con un campo magnético constante, no hay flujo variable en el tiempo a través del contorno:
\[\oint_{L} \textbf{E} \cdot \textbf{dl} = \int_{1}^{2} E_{\textrm{r}} d \textrm{r} + \int_{3}^{4} \underbrace{\textbf{E} \cdot \textbf{dl}}_{-v_{r}} = 0 \nonumber \]
El uso de (14) en (15) produce el voltaje del terminal como
\[v_{r} = \int_{R_{i}}^{R_{0}} \bigg( \frac{i_{r}}{2 \pi \textrm{r} \sigma d} - \omega \textrm{r} B_{0} \bigg) d \textrm{r} \\ \frac{i_{r}}{2 \pi \sigma d} \ln \frac{R_{0}}{R_{i}} - \frac{\omega B_{0}}{2} (R_{0}^{2}-R_{i}^{2}) \\ = i_{r}R_{r} - G \omega i_{f} \nonumber \]
donde\(R_{r}\) es la resistencia interna del rotor del disco y G se llama el coeficiente de velocidad:
\[R_{r} = \frac{\ln (R_{0}/R_{i})}{2 \pi \sigma d}, \: \: \: G = \frac{\mu_{0}N}{2s} (R_{0}^{2} - R_{i}^{2}) \nonumber \]
Despreciamos el campo automagnético debido a la corriente del rotor, asumiendo que es mucho menor que el campo aplicado\(B_{0}\), pero se representa en el circuito de rotor equivalente en la Figura 6-15b como la autoinductancia\(L_{r}\) en serie con una resistencia y una fuente de voltaje de velocidad linealmente dependiente de la corriente de campo. La bobina de campo estacionaria está representada por su autoinductancia y resistencia.
Para un disco de cobre (\(\sigma \approx 6 \times 10^{7}\)siemen/m) de espesor 1mm que gira a 3600 rpm (\(\omega \approx 120 \pi\)radianes/seg) con radios externo e interno\(R_{0} = 10\) cm y\(R_{i} = 1\) cm en un campo magnético de\(B_{0}\) = 1 tesla, el voltaje de circuito abierto es
\[v_{\alpha} = - \frac{\omega B_{0}}{2}(R_{0}^{2} - R_{i}^{2}) \approx -1.9 \textrm{V} \nonumber \]
mientras que la corriente de cortocircuito es
\[i_{\textrm{sc}} = \frac{v_{\textrm{oc}}}{\ln (R_{0}/R_{i})} 2 \pi \sigma d \approx 3 \times 10^{5} \textrm{amp} \nonumber \]
Los generadores homopolares suelen ser dispositivos de alta corriente y baja tensión. El par electromagnético en el disco debido a la fuerza de Lorentz es
\[\textbf{T} = \int_{\phi = 0}^{2 \pi} \int_{z=0}^{d} \int_{\textrm{r} = R_{i}}^{R_{0}} \textrm{r} \textbf{i}_{\textrm{r}} \times (\textbf{J} \times \textbf{B}) \textrm{r} d \textrm{r} d \phi d z \\ = -r_{r}B_{0} \textbf{i}_{z} \int_{R_{i}}^{R_{0}} \textrm{r} d \textrm{r} \\ = - \frac{i_{r} B_{0}}{2} (R_{0}^{2} - R_{i}^{2}) \textbf{i}_{z} \\ = - G i_{f} i_{r} \textbf{i}_{z} \nonumber \]
El signo negativo indica que la fuerza de Lorentz actúa sobre el disco en dirección opuesta al movimiento. Un par externo igual en magnitud pero opuesto en dirección a (20) es necesario para girar el eje.
Este dispositivo también se puede operar como un motor si se impone una corriente del rotor en el disco (\(i_{r} < 0\)). Entonces el par eléctrico hace que el disco gire.
(b) Generador autoexcitado
Para el funcionamiento del generador es necesario girar el eje y suministrar una corriente de campo para generar el campo magnético. Sin embargo, si la bobina de campo está conectada a los terminales del rotor, como en la Figura 6-16a, el generador puede suministrar su propia corriente de campo. El circuito equivalente para operación autoexcitada se muestra en la Figura 6-16b donde tiene la conexión en serie\(i_{r} = i_{f}\).
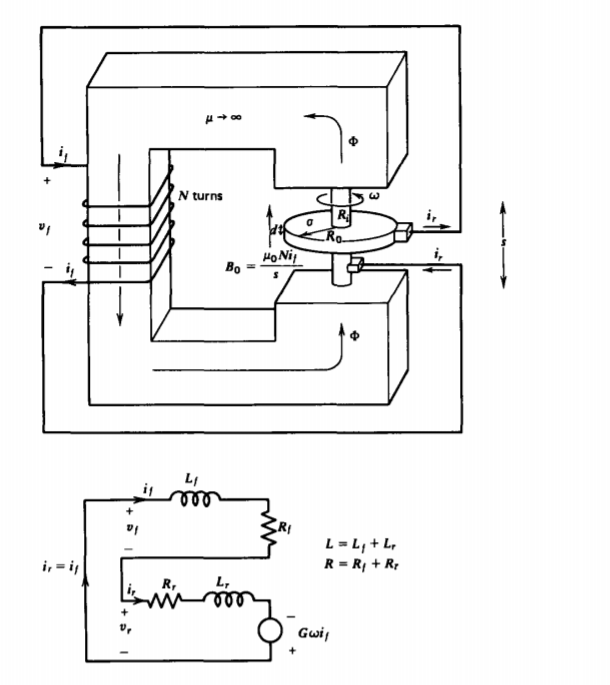
La ley de voltaje de Kirchoff alrededor del bucle es
\[L \frac{di}{dt} + i(R-G \omega) = 0, \: \: \: \: R = R_{r} + R_{f}, \: \: \: \: L = L_{r} + L_{f} \nonumber \]
donde R y L son la resistencia e inductancia en serie de la bobina y el disco. La solución a (21) es
\[i = I_{0} e^{-[(R-G \omega)/L]t \nonumber \]
donde\(I_{0}\) es la corriente inicial a t = 0. Si el factor exponencial es positivo
\[G \omega > R \nonumber \]
la corriente crece con el tiempo por pequeña\(I_{0}\) que sea. En la práctica,\(I_{0}\) se genera por fluctuaciones aleatorias (ruido) debidas al magnetismo residual en el núcleo de hierro. El crecimiento exponencial está limitado por la saturación del núcleo magnético para que la corriente alcance un valor de estado estacionario. Si el disco gira en sentido opuesto (\(\omega\)<0), no se puede satisfacer la condición de (23). Entonces es necesario que la conexión de la bobina de campo se invierta para que\(i_{r} = -i_{f}\). Tal modelo de dinamo ha sido utilizado como modelo del origen del campo magnético terrestre.
(c) Operación de CA Autoexcitada
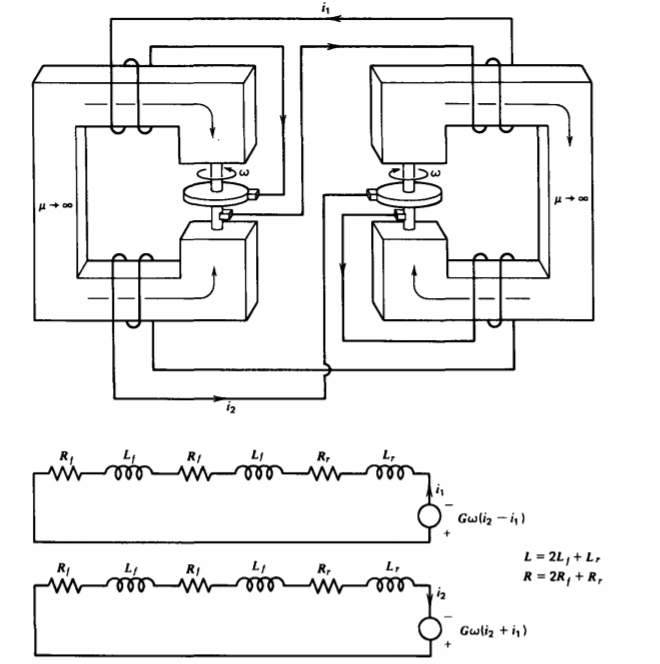
Dos de estos generadores acoplados pueden generar espontáneamente energía de CA bifásica si se conectan dos devanados de campo independientes, como en la Figura 6-17. Los devanados de campo están conectados de manera que si el flujo a través de los dos devanados en una máquina suma, restan en la otra máquina. Esto explica la diferencia de señal en los voltajes de velocidad en los circuitos equivalentes,
\[L = \frac{di_{1}}{dt} + (R-G \omega) i_{1} + G \omega i_{2} = 0 \\ L \frac{di_{2}}{dt} + (R-G \omega) i_{2} - G \omega i_{1} = 0 \nonumber \]
donde L y R son la inductancia y resistencia en serie total. Cada uno de los discos se gira a la misma velocidad angular\(\omega\).
Dado que (24) son lineales con coeficientes constantes, las soluciones son de la forma
\[i_{1} = I_{1} e^{st}, \: \: \: \: i_{2} = I_{2} e^{st} \nonumber \]
que cuando se sustituye de nuevo en (24) rinde
\[(Ls + R - G \omega) I_{1} + G \omega I_{2} = 0 \\ -G \omega I_{1} + (Ls + R - G \omega) I_{2} = 0 \nonumber \]
Para soluciones no triviales, el determinante de los coeficientes de\(I_{1}\) y\(I_{2}\) debe ser cero,
\[(Ls + R - G \omega)^{2} = -(G \omega)^{2} \nonumber \]
que cuando se resuelve para s produce las frecuencias naturales conjugadas complejas,
\[s = - \frac{(R- G \omega)}{L} \pm j \frac{G \omega}{L} \\ I_{1}/I_{2} = \pm j \nonumber \]
donde las corrientes están desfasadas 90°. Si la parte real de s es positiva, el sistema se autoexcita para que cualquier perturbación
crece a una tasa exponencial:
\[G \omega > R \nonumber \]
La parte imaginaria de s produce la frecuencia de oscilación
\[\omega_{0} = \textrm{Im} (s) = G \omega/L \nonumber \]
Nuevamente, la saturación del núcleo limita el crecimiento exponencial de manera que los resultados de potencia bifásica. Tal modelo puede ayudar a explicar las reversiones periódicas en el campo magnético de la tierra cada pocos cientos de miles de años.
d) Reversiones periódicas de la velocidad del motor
Si el devanado de campo de un motor es excitado por una corriente continua, como en la Figura 6-18, con los terminales del rotor conectados a un generador cuyos terminales de campo y rotor están en serie, la ecuación del circuito es
\[\frac{di}{dt} + \frac{(R - G_{g}\omega_{g})}{L} i = \frac{G_{m} \omega_{m}}{L} I_{f} \nonumber \]
donde L y R son las inductancias y resistencias de la serie total. La velocidad angular del generador\(\omega_{g}\) es externamente
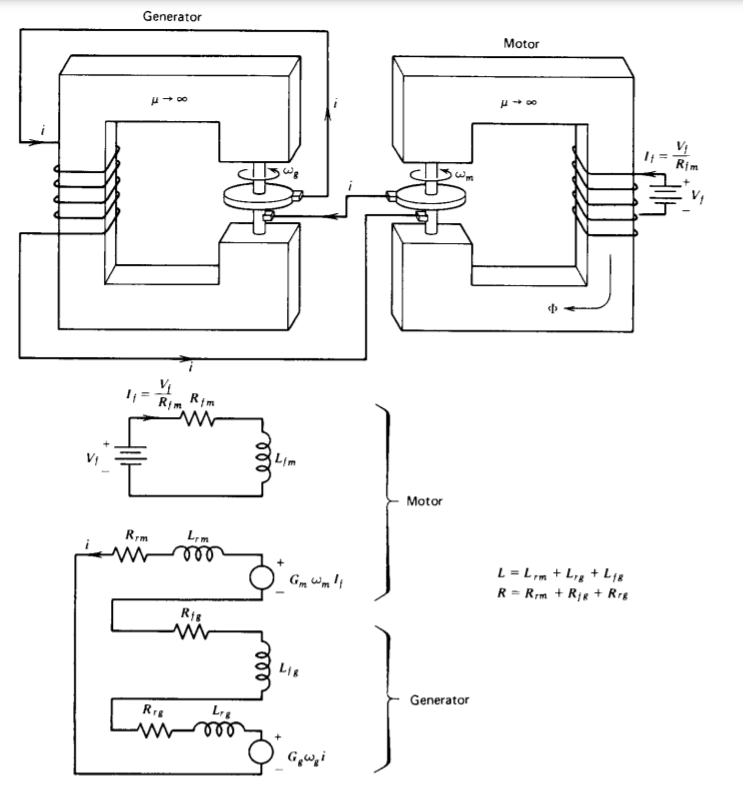
constreñido a ser una constante. La aceleración angular del eje del motor es igual al par de (20),
\[J \frac{d \omega_{m}}{dt} = - G_{m}I_{f}i \nonumber \]
donde J es el momento de inercia del eje y\(I_{f} = V_{f}/R_{fm}\) es la corriente constante del campo del motor.
Las soluciones de estas ecuaciones diferenciales de coeficiente constante lineal acopladas son de la forma
\[i = I e^{st} \\ \omega = W e^{st} \nonumber \]
que cuando se vuelve a sustituir en (31) y (32) rinden
\[I \bigg( s + \frac{R - G_{g} \omega_{g}}{L} \bigg) - W \bigg(\frac{G_{m}I_{f}}{L} \bigg) = 0 \\ I \bigg( \frac{G_{m} I_{f}}{J} \bigg) + W s = 0 \nonumber \]
Nuevamente, para soluciones no triviales el determinante de coeficientes de I y W debe ser cero,
\[s \bigg(s + \frac{R - G_{g} \omega_{g}}{L} \bigg) + \frac{(G_{m} I_{f})^{2}}{JL} =0 \nonumber \]
que cuando se resuelve para s rendimientos
\[s = - \frac{(R - G_{g} \omega_{g})}{2L} \pm \bigg[ \bigg( \frac{R-G_{g}\omega_{g}}{2L} \bigg)^{2} - \frac{(G_{m}I_{f})^{2}}{JL} \bigg]^{1/2} \nonumber \]
Para la autoexcitación la parte real de s debe ser positiva,
\[G_{g} \omega_{g} > R \nonumber \]
mientras que las oscilaciones ocurrirán si s tiene una parte imaginaria,
\[\frac{(G_{m}I_{f})^{2}}{JL} > \bigg( \frac{R-G_{g}\omega_{g}}{2L} \bigg)^{2} \nonumber \]
Ahora, tanto la corriente como la velocidad angular del eje oscilan espontáneamente con el tiempo.
* Parte del tratamiento en esta sección es similar al desarrollado en: H. H. Woodson y J. R. Melcher, Dinámica Electromecánica, Parte I, Wiley, N. Y., 1968, Ch. 6
6-3-4 Motores y Generadores Básicos
(a) Máquinas ac
Los voltajes alternos se generan a partir de un campo magnético de cc mediante la rotación de una bobina, como en la Figura 6-19. Un voltaje de salida se mide mediante anillos deslizantes a través de escobillas de carbón. Si el bucle del área A es vertical a t = 0 enlazando flujo cero, el flujo impuesto
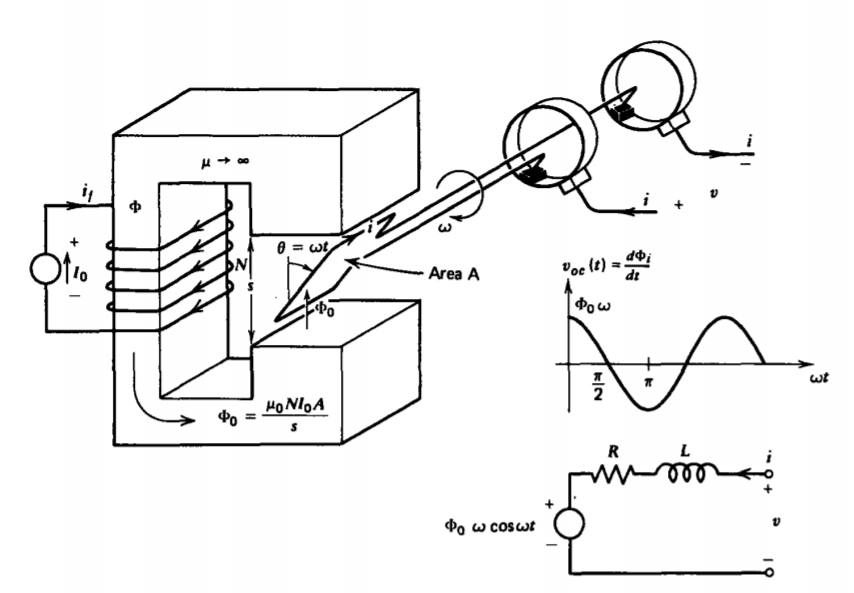
a través del bucle en cualquier momento, varía sinusoidalmente con el tiempo debido a la rotación como
\[\Phi_{i} = \Phi_{0} \sin \omega t \nonumber \]
La ley de Faraday aplicada a un contorno estacionario que pasa instantáneamente a través del cable y luego da el voltaje del terminal como
\[v = iR + \frac{d \Phi}{dt} = iR + L \frac{di}{dt} + \Phi_{0} \omega \cos \omega t \nonumber \]
donde R y L son la resistencia e inductancia del cable. El flujo total es igual al flujo impuesto de (39) así como al autoflujo (contabilizado por L) generado por la corriente i. El circuito equivalente es entonces similar al del generador homopolar, pero el término de voltaje de velocidad ahora es sinusoidal en el tiempo
(b) Máquinas dc
Las máquinas DC tienen una configuración similar excepto que el anillo colectando se divide en dos secciones, como en la Figura 6-20a. Entonces siempre que el voltaje de salida tiende a cambiar de signo, los terminales también se invierten dando la forma de onda mostrada, que es de una polaridad con variaciones periódicas de cero a un valor pico.
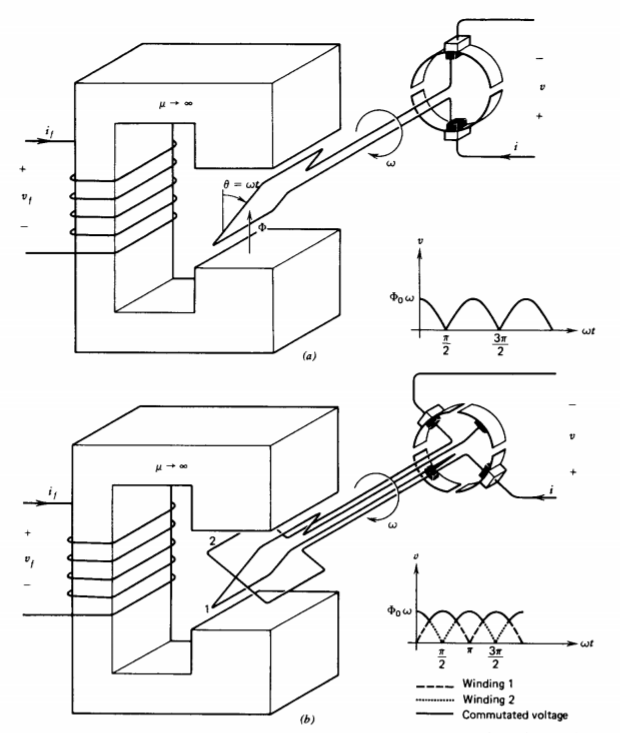
La forma de onda de voltaje se puede suavizar usando un conmutador de cuatro secciones y colocando una segunda bobina perpendicular a la primera, como en la Figura 6-20b. Esta segunda bobina genera ahora su voltaje pico cuando la primera bobina genera voltaje cero. Con más secciones de colector y más bobinas, el voltaje de CC se puede hacer tan suave como se desee.
6-3-5 Máquinas MHD
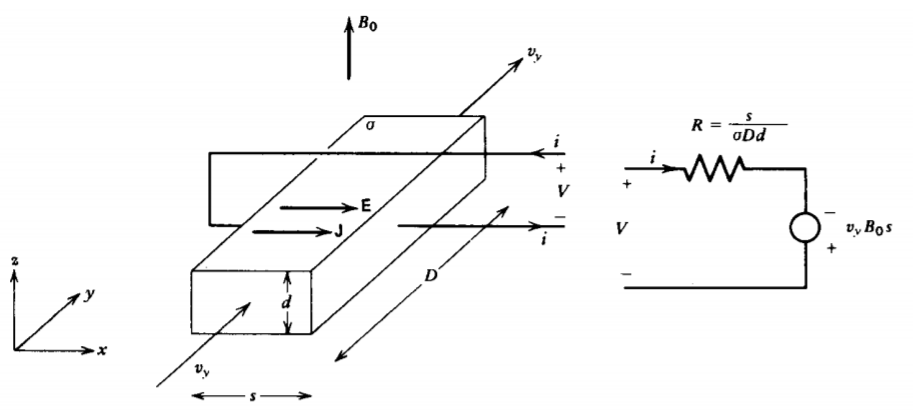
Las máquinas magnetohidrodinámicas se basan en los mismos principios que las máquinas giratorias, reemplazando el rotor rígido por un fluido conductor. Para la máquina lineal de la Figura 6-21, un fluido con conductividad óhmica\(\sigma\) que fluye con velocidad\(v_{y}\) se mueve perpendicularmente a un campo magnético aplicado\(B_{0} \textbf{i}_{z}\). El voltaje terminal V está relacionado con el campo eléctrico y la corriente como
\[\textbf{E} = \textbf{i}_{x} \frac{V}{s}, \: \: \: \: \textbf{J} = \sigma (\textbf{E} + \textbf{v} \times \textbf{B}) = \sigma \bigg( \frac{V}{s} + v_{y}B_{0} \bigg) \textbf{i}_{x} = \frac{i}{Dd} \textbf{i}_{x} \nonumber \]
que se puede reescribir como
\[V = iR - v_{y} B_{0}s \nonumber \]
que tiene un circuito equivalente similar al del generador homopolar.
La fuerza en el canal es entonces
\[\textbf{f} = \int_{\textrm{V}} \textbf{J} \times \textbf{B} d \textrm{V} \\ = -i B_{0} s \textbf{i}_{y} \nonumber \]
otra vez opuesto al movimiento fluido.
6-3-6 Paradojas
La ley de Faraday es propensa al mal uso, lo que ha llevado a numerosas paradojas. La confusión surge porque lo mismo
la contribución puede surgir ya sea del lado de la fuerza electromotriz de la ley, como un voltaje de velocidad cuando un conductor se mueve ortogonal a un campo magnético, o como una tasa de tiempo de cambio de flujo a través del contorno. Este término de flujo en sí tiene dos contribuciones debido a un campo magnético variable en el tiempo o debido a un contorno que cambia su forma, tamaño u orientación. Con todas estas contribuciones potenciales suele ser fácil faltar a un término o duplicar el conteo.
(a) Una máquina sin commutator*
Muchas personas han tratado de hacer una máquina dc sin trabajo pero fue en ningún resultado. Un nuevo intento fallido se ilustra en la Figura 6-22, donde un hilo altamente conductor se hace vibrar dentro del hueco de un circuito magnético con velocidad sinusoidal:
\[v_{x} = v_{0} \sin \omega t \nonumber \]
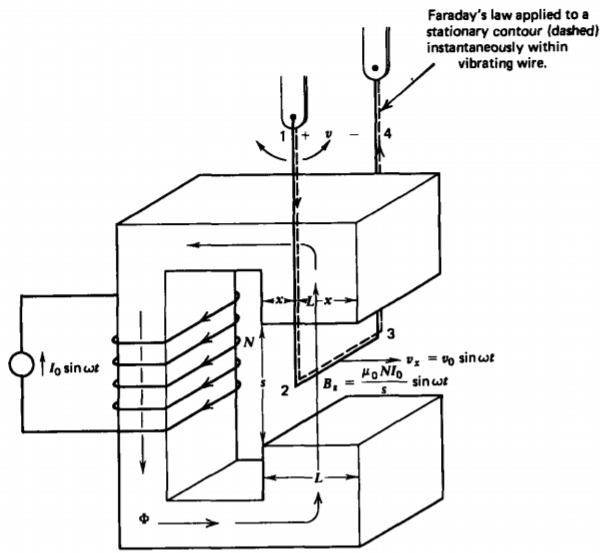
La corriente sinusoidal impone la densidad de flujo del entrehierro a la misma frecuencia\(\omega\):
\[B_{z} = B_{0} \sin \omega t, \: \: \: \: B_{0} = \mu_{0} NI_{0}/s \nonumber \]
La aplicación de la ley de Faraday a un contorno estacionario instantáneamente dentro del cable de circuito abierto produce
\[\oint_{L} \textbf{E} \cdot \textbf{dl} = \int_{1}^{2} \textbf{E} \nearrow^{0} \cdot \textbf{dl} + \int_{2}^{3} \underbrace{\textbf{E \cdot \textbf{dl}}_{\textbf{E} = - \textbf{v} \times \textbf{B}} + \int_{3}^{4} \textbf{E} \nearrow^{0} \cdot \textbf{dl} + \int_{4}^{1} \underbrace{\textbf{E} \cdot \textbf{dl}}_{- \nu} \\ = - \frac{d}{dt} \int_{S} \textbf{B} \cdot \textbf{dS} \nonumber \]
donde el campo eléctrico dentro del cable altamente conductor medido por un observador que se mueve con el cable es cero. El campo eléctrico en el tramo 2-3 dentro del entrehierro viene dado por (11), donde\(\textbf{E}'=0\) mientras que el tramo 4-1 define el voltaje del terminal. Si argumentamos erróneamente que el término de flujo en el lado derecho es cero porque el campo magnético B es perpendicular a dS, el voltaje del terminal es
\[v = v_{x} B_{z} l = v_{0} B_{0} l \sin^{2} \omega t \nonumber \]
que tiene un valor promedio de tiempo de cc. Desafortunadamente, este resultado no está completo porque olvidamos incluir el flujo que gira la esquina en el núcleo magnético y pasa perpendicularmente por nuestro contorno. Solo el flujo a la derecha del alambre pasa a través de nuestro contorno, que es la fracción\((L-x)/L\) del flujo total. Entonces la correcta evaluación de (46) es
\[-v + v_{x}B_{z}l = + \frac{d}{dt}[(L-x) B_{z}l] \nonumber \]
donde x se trata como una constante porque el contorno es estacionario. El cambio de signo en el lado derecho surge porque el flujo pasa por el contorno en la dirección opuesta a su normal definida por la regla de la derecha. El voltaje es entonces
\[v = v_{x} B_{z} l - (L-x) l \frac{dB_{z}}{dt} \nonumber \]
donde la posición del cable se obtiene integrando (44),
\[x = \int v_{x} dt = - \frac{v_{0}}{\omega} (\cos \omega t - 1) + x_{0} \nonumber \]
y\(x_{0}\) es la posición del cable en t = 0. Entonces (49) se convierte
\[v = l \frac{d}{dt} (x B_{z}) - Ll \frac{dB_{z}}{dt} \\ = B_{0} lv_{0} \bigg[ \bigg( \frac{x_{0} \omega}{v_{0}} + 1 \bigg) \cos \omega t - \cos 2 \omega t \bigg] - L l B_{0} \omega \cos \: \omega t \nonumber \]
que tiene un promedio de tiempo cero.
(b) Cambios en el flujo magnético debido a la conmutación
Cambiar la configuración de un circuito usando un interruptor no da como resultado una fuerza electromotriz a menos que cambie el flujo magnético en sí.
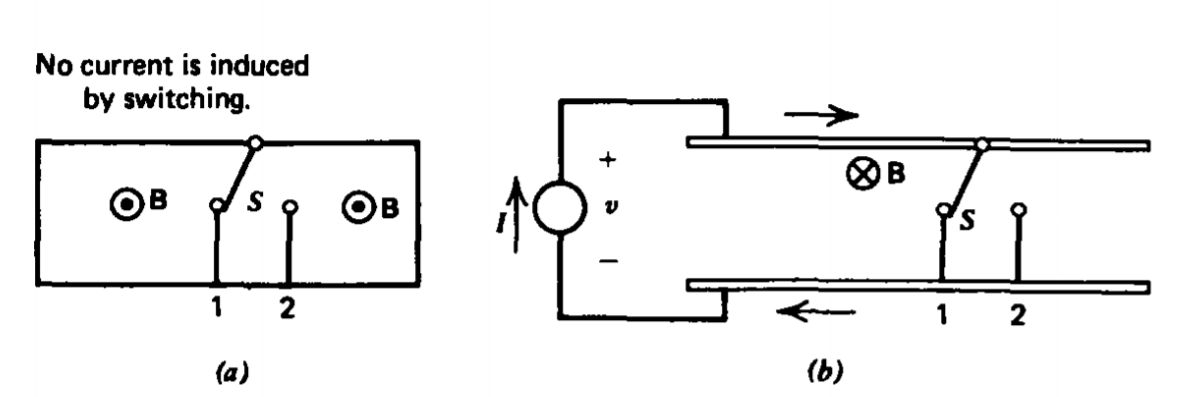
En la Figura 6-23a, el campo magnético a través del bucle se impone externamente y es independiente de la posición del interruptor. Mover el interruptor no induce un EMF porque el flujo magnético a través de cualquier superficie permanece sin cambios.
En la Figura 6-23b, una fuente de corriente continua está conectada a un circuito a través de un interruptor S. Si el interruptor se mueve instantáneamente del contacto 1 al contacto 2, el campo magnético debido a la corriente de fuente I cambia. El flujo a través de cualquier área fija ha cambiado, lo que resulta en un EMF.
(c) Número de vueltas variables en el tiempo en una bobina**
Si el número de vueltas en una bobina está cambiando con el tiempo, como en la Figura 6-24, el voltaje es igual a la tasa de tiempo de cambio de flujo a través de la bobina. Es el voltaje entonces
\[v \overset{?}{=} N \frac{d \Phi}{dt} \nonumber \]
o
\ [v\ overset {?} {=}\ frac {d} {dt} (N\ Phi) = N\ frac {d\ phi} {dt} +\ phi\ frac {dN} {dt}
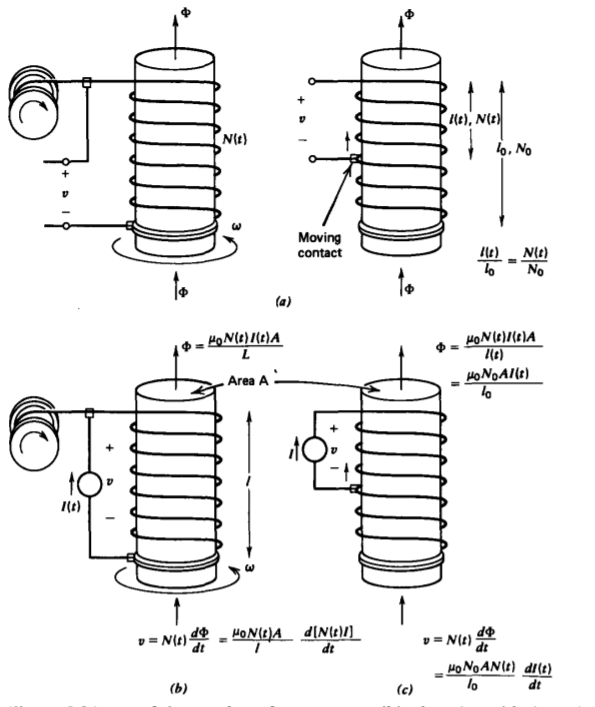
Para el primer caso un flujo de CC no genera voltaje mientras que el segundo lo hace.
Utilizamos la ley de Faraday con un contorno estacionario instantáneamente dentro del cable. Debido a que el contorno es estacionario, su área de NA no está cambiando con el tiempo y así se puede tomar fuera de la derivada del tiempo en el término de flujo de la ley de Faraday para que el voltaje esté dado por (52) y (53) sea incorrecto. Tenga en cuenta que no hay contribución de voltaje de velocidad en la fuerza electromotriz porque la velocidad del cable está en la misma dirección que el contorno (\(\textbf{v} \times \textbf{B} \cdot \textbf{dl} = 0\)).
Si el flujo (en\(\Phi\) sí depende del número de vueltas, como en la Figura 6-24b, puede haber una contribución a la tensión incluso si la corriente de excitación es dc. Esto es cierto para los giros que se enrollan sobre el cilindro en la Figura 6-24b. Para la configuración de cambio de tomas en la Figura 6-24c, con giros enrollados uniformemente, la relación de vueltas a longitud efectiva es constante de modo que una corriente continua aún no generará voltaje.
* H. Sohon, Ensayos Eléctricos para Recreación. Ingeniería Eléctrica, mayo (1946), p. 294.
** L. V. Bewley. Enlaces de Flujo e Inducción Electromagnética. Macmillan, Nueva York, 1952.


