6.4: El método energético para las fuerzas

Si se conoce la distribución de corriente, el campo magnético se puede encontrar directamente a partir de las leyes de Biot-Savart o Ampere. Sin embargo, cuando el campo magnético varía con el tiempo, el campo eléctrico generado dentro de un conductor óhmico induce más corrientes que también contribuyen al campo magnético.

Modelo de Resistor-Inductor 6-4-1

Una carcasa conductora delgada de\(R_{i}\) grosor\(\Delta\) de radio y profundidad\(l\) se coloca dentro de un cilindro conductor más grande, como se muestra en la Figura 6-25. \(I_{0}\)Se aplica una corriente escalonada a t =0 al cilindro más grande, generando una corriente superficial\(\textbf{K} = (I_{0}/l) \textbf{i}_{\phi}\). Si la longitud\(l\) es mucho mayor que el radio exterior\(R_{0}\), el campo magnético es cero fuera del cilindro y uniforme por dentro para\(R_{i} < r < R_{0}\). Luego de la condición límite sobre la discontinuidad de H tangencial dada en la Sección 5-6-1, tenemos

\[\textbf{H}_{0} = \dfrac{I_{0}}{l} \textbf{i}_{z}, \: \: \: \: R_{i} < r < R_{0} \nonumber \]

El campo magnético es diferente dentro de la carcasa conductora debido a la corriente inducida, que a partir de la ley de Lenz, fluye en dirección opuesta a la corriente aplicada. Debido a que se supone que la carcasa es muy delgada (\(\Delta << R_{1}\)), esta corriente inducida puede considerarse una corriente superficial relacionada con la corriente volumétrica y el campo eléctrico en el conductor como

\[K_{\phi} = J_{\phi} \Delta = (\sigma \Delta) E_{\phi} \nonumber \]

El producto (\(\sigma \Delta\)) se llama conductividad superficial. Luego, los campos magnéticos a ambos lados de la capa delgada también están relacionados por la condición límite de la Sección 5-6-1:

\[H_{i} - H_{0} = K_{\phi} = (\sigma \Delta) E_{\phi} \nonumber \]

Figura 6-25 Un cambio escalonado en el campo magnético hace que la corriente inducida dentro de un conductor óhmico fluya en la dirección donde su autoflujo se opone al flujo impuesto externamente. La disipación óhmica hace que la corriente inducida disminuya exponencialmente con el tiempo con una constante de\(L/R\) tiempo.

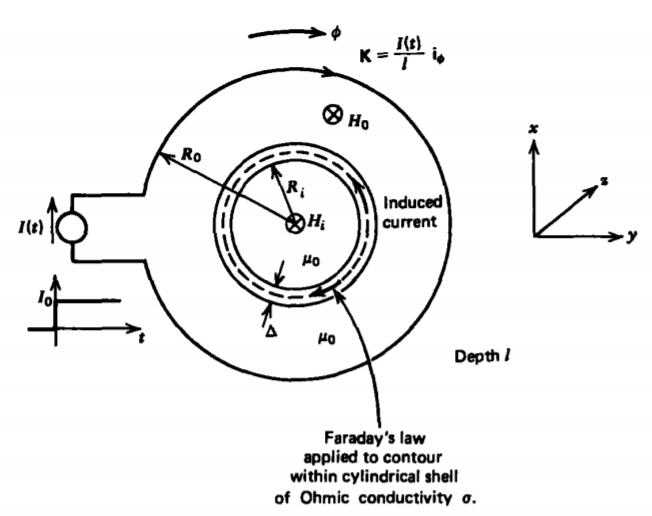
Aplicando la ley de Faraday a un contorno dentro de los rendimientos de la cáscara conductora

\[\oint_{L} \textbf{E} \cdot \textbf{dl} = - \dfrac{d}{dt} \int_{S} \textbf{B} \cdot \textbf{dS} \Rightarrow E_{\phi} 2 \pi R_{i} = - \mu_{0} \pi R^{2}_{i} \dfrac{dH_{i}}{dt} \nonumber \]

donde solo el flujo magnético debido a que\(H_{i}\) pasa a través del contorno. Luego, al usar (1) - (3) en (4) se obtiene una sola ecuación en\(H_{i}\):

\[\dfrac{dH_{i}}{dt} + \dfrac{H_{i}}{\tau} = \dfrac{I(t)}{l \tau}, \: \: \: \: \tau = \dfrac{\mu_{0} R_{i} \sigma \Delta}{2} \nonumber \]

donde reconocemos la constante de tiempo\(\tau\) como la relación entre la autoinductancia del proyectil y la resistencia:

\[: = \dfrac{\Phi}{K_{\phi}l} = \dfrac{\mu_{0} \pi R^{2}_{i}}{l}, \: \: \: \: R = \dfrac{2 \pi R_{i}}{\sigma l \Delta}, \: \: \: \: \tau = \dfrac{L}{R} = \dfrac{\mu_{0}R_{i} \sigma \Delta}{2} \nonumber \]

La solución a (5) para una corriente escalonada con campo magnético inicial cero es

\[H_{i} = \dfrac{I_{0}}{l}(1 - e^{-t/tau}) \nonumber \]

Inicialmente, el campo magnético es excluido del interior de la carcasa conductora por la corriente inducida. Sin embargo, la disipación óhmica provoca que la corriente inducida disminuya con el tiempo para que el campo magnético pueda penetrar a través del caparazón con constante de tiempo característica\(\tau\).

* Gran parte del tratamiento de esta sección es similar al de H. H. Woodson y J. R. Melcher, Dinámica Electromecánica, ParII, Wiley, N. Y., 1968, Ch. 7.

6-4-2 La Ecuación de Difusión Magnética

La solución transitoria para una cubierta conductora delgada podría resolverse usando las leyes integrales porque la geometría restringía la corriente inducida a fluir azimutalmente sin variaciones radiales. Si no se conoce directamente la densidad de corriente, se hace necesario resolver de manera autoconsistente la densidad de corriente con los campos eléctrico y magnético:

\[\nabla \times \textbf{E} = - \dfrac{\partial \textbf{B}}{\partial t} \: \textrm{(Faraday's law)} \nonumber \]

\[ \nabla \times \textbf{H} = \textbf{J}_{f} \: \textrm{(Ampere's law)} \nonumber \]

\[ \nabla \cdot \textbf{B} = 0 \: \textrm{(Gauss's law)} \nonumber \]

Para materiales magnéticos lineales con permeabilidad constante\(\mu\) y conductividad óhmica constante que\(\sigma\) se mueven con velocidad U, las leyes constitutivas son

\[\textbf{B} = \mu \textbf{J}, \: \: \: \: \textbf{J}_{f} = \sigma (\textbf{E} + \textbf{U} \times \mu \textbf{H}) \nonumber \]

Podemos reducir (8) - (11) a una sola ecuación en el campo magnético tomando el rizo de (9), usando (8) y (11) como

\[\nabla \times (\nabla \times \textbf{H}) = \nabla \times \textbf{J}_{f} \\ = \sigma [ \nabla \times \textbf{E} + \mu \nabla \times (\textbf{U} \times \textbf{H})] \\ = \mu \sigma \bigg( - \dfrac{\partial \textbf{H}}{\partial t} + \nabla \times (\textbf{U} \times \textbf{H}) \bigg) \nonumber \]

El producto cruzado doble de H puede simplificarse usando la identidad del vector

\[\nabla \times (\nabla \times \textbf{H}) = \nabla (\nabla \cancelto{0}{\cdot} \textbf{H}) - \nabla^{2} \textbf{H} \\ \Rightarrow \dfrac{1}{\mu \sigma} \nabla^{2} \textbf{H} = \dfrac{\partial \textbf{H}}{\partial t} - \nabla \times (\textbf{U} \times \textbf{H}) \nonumber \]

donde H no tiene divergencia de (10). Recuerde que el operador laplaciano en el lado izquierdo de (13) también diferencia los vectores unitarios direccionalmente dependientes en coordenadas cilíndricas (\(\textbf{i}_{\textrm{r}}\)y\(\textbf{i}_{\phi}\)) y esféricas (\(\textbf{i}_{r}, \: \textbf{i}_{\theta},\)y\(\textbf{i}_{\phi}\)).

6-4-3 Solución Transitoria sin Movimiento (U =0)

Se enciende una corriente escalonada a t =0, en la geometría de placa paralela mostrada en la Figura 6-26. Por la regla de la derecha y con el descuido de la franja, el campo magnético está en la dirección z y solo depende de la coordenada x,\(B_{z} (x,t)\), de manera que (13) se reduce a

\[\dfrac{\partial^{2}H_{z}}{\partial x^{2}} - \sigma \mu \dfrac{\partial H_{z}}{\partial t} = 0 \nonumber \]

que es similar en forma a la ecuación de difusión de un cable resistivo-capacitivo distribuido desarrollado en la Sección 3-6-4.

En el estado estacionario dc, el segundo término es cero de manera que la solución en cada región es de la forma

\[\dfrac{\partial^{2}H_{z}}{\partial x^{2}} = 0 \Rightarrow H_{z} = ax + b \nonumber \]

Figura 6-26 (a) Una fuente de corriente se enciende instantáneamente a t = 0. El campo magnético resultante dentro del conductor óhmico permanece continuo y por lo tanto es cero a t = 0 requiriendo una corriente superficial en x =0. (b) Para tiempos posteriores el campo magnético y la corriente se difunden en el conductor con mayor constante de tiempo\(\tau = \sigma \mu d^{2}/\pi^{2}\) hacia un estado estacionario de corriente uniforme con un campo magnético lineal.

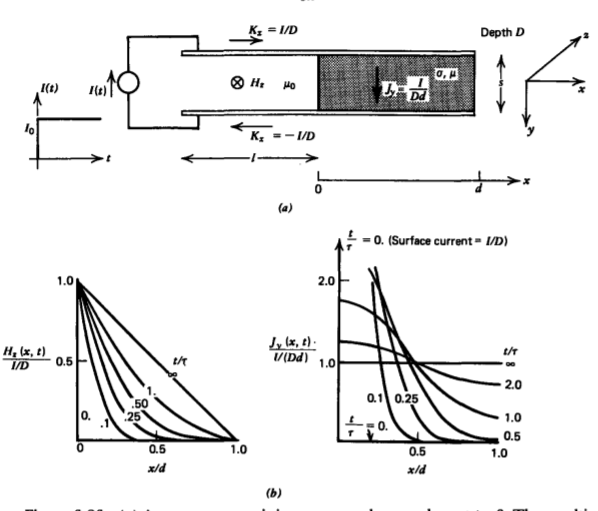
donde a y b se encuentran a partir de las condiciones límite. La corriente en los electrodos se extiende inmediatamente a una distribución superficial uniforme\(\pm (I/D) \textbf{i}_{x}\), viajando desde el electrodo superior al inferior uniformemente a través del conductor óhmico. Entonces, el campo magnético es uniforme en la región del espacio libre, disminuyendo linealmente a cero dentro del conductor óhmico siendo continuo a través de la interfaz en x =0:

\[\lim_{t \rightarrow \infty} H_{z} (x) = \left \{ \begin{matrix} \dfrac{I}{D}, \: \: \: \: -l \leq x \leq 0 \\ \dfrac{I}{Dd} (d-x), & 0 \leq x \leq d \end{matrix} \right. \nonumber \]

En la región del espacio libre donde\(\sigma = 0\), el campo magnético permanece constante para siempre. Dentro de la losa conductora, hay un transitorio de carga inicial a medida que el campo magnético se acumula hasta la distribución lineal de estado estacionario en (16). Debido a que (14) es una ecuación lineal, para la solución total del campo magnético en función del tiempo y el espacio, usamos superposición y adivinamos una solución que es la suma de la solución de estado estacionario en (16) y una solución transitoria que muere con el tiempo:

\[H_{z} (x,t) = \dfrac{I}{Dd}(d-x) + \hat{H} (x) e^{-\alpha t} \nonumber \]

Seguimos los mismos procedimientos que para el cable con pérdida en la Sección 3-6-4. En este punto desconocemos la función\(\hat{H}(x)\) o el parámetro\(\alpha\). Sustituir la solución supuesta de (17) de nuevo en (14) produce la ecuación diferencial ordinaria

\[\dfrac{d^{2} \hat{H}(x)}{dx^{2}} + \sigma \mu \alpha \hat{H} (x) = 0 \nonumber \]

que cuenta con las soluciones trigonométricas

\[\hat{H}(x) = A_{1} sin \sqrt{\sigma \mu \alpha} x + A_{2} \cos \sqrt{\sigma \mu \alpha} x \nonumber \]

Dado que la parte independiente del tiempo en (17) ya cumple con las condiciones límite de

\[H_{z}(x=0) = I/D \\ H_{z} (x=d) =0 \nonumber \]

la parte transitoria de la solución debe ser cero en los extremos

\[\hat{H}(x=0) = 0 \Rightarrow A_{2} = 0 \\ \hat{H}(x=d) = 0 \Rightarrow \sin \sqrt{\sigma \mu \alpha} d =0 \nonumber \]

que arroja los valores permitidos de\(\alpha\) as

\[\sqrt{\sigma \mu \alpha} d = n \pi \Rightarrow \alpha_{n} = \dfrac{1}{\mu \sigma} \bigg( \dfrac{n \pi}{d} \bigg)^{2}, \: \: \: \: n = 1,2,3... \nonumber \]

Dado que hay un número infinito de valores permitidos de\(\alpha\), la solución más general es la superposición de todas las soluciones permitidas:

\[H_{z} (x,t) = \dfrac{I}{Dd} (d - x) + \sum_{n=1}^{\infty} A_{n} \sin \dfrac{n \pi x}{d} e^{- \alpha_{n}t} \nonumber \]

Esta relación satisface las condiciones de contorno pero no las condiciones iniciales en t = 0 cuando la corriente se enciende por primera vez. Antes de que la corriente dé su paso a t =0, el campo magnético es cero en la losa. Justo después de encender la corriente, el campo magnético debe permanecer cero. La ley de Faraday haría infinito el campo eléctrico y así la densidad de corriente dentro de la losa, que es no física. Así imponemos la condición inicial

\[H_{z} (x,t = 0) = 0 = \dfrac{I}{Dd} (d-x) + \sum_{n=1}^{\infty} A_{n} \sin \dfrac{n \pi x}{d} \nonumber \]

lo que nos permitirá resolver para las amplitudes\(A_{n}\) multiplicando (24) por sin (\(m \pi x/d\)) y luego integrando sobre x de 0 a d:

\[0 = \dfrac{I}{Dd} \int_{0}^{d} (d-x) \sin \dfrac{m \pi x}{d} dx + \sum_{n=1}^{\infty} A_{n} \int_{0}^{d} \sin \dfrac{n \pi x}{d} \sin \dfrac{m \pi x}{d} dx \nonumber \]

El primer término en el lado derecho es fácilmente integrable* mientras que el producto de términos sinusoidales se integra a cero a menos que m = n, rindiendo

\[A_{m} = - \dfrac{2I}{m \pi D} \nonumber \]

La solución total es así

\[H_{z} (x,t) = \dfrac{I}{D} \bigg(1 - \dfrac{x}{d} - 2 \sum_{n=1}^{\infty} \dfrac{\sin (n \pi x/d)}{n \pi} e^{-n^{2} t/\tau} \bigg) \nonumber \]

donde definimos la constante de tiempo de difusión magnética continua fundamental\(\tau\) como

\[\tau = \dfrac{1}{\alpha_{1}} = \dfrac{\mu \sigma d^{2}}{\pi^{2}} \nonumber \]

análogo a la constante de tiempo del parámetro agrupado de (5) y (6).

El campo magnético se acerca al estado estacionario en tiempos largos en comparación con\(\tau\). Para un conductor perfecto (\(\sigma \rightarrow \infty\)), esta vez es infinita y el campo magnético queda excluido para siempre de la losa. La corriente entonces fluye solo a lo largo de la superficie x = 0. Sin embargo, incluso para cobre (\(\sigma \approx 6 \times 10^{7}\)siemens/m) de 10 cm de espesor, la constante de tiempo es\(\tau \approx \80\) mseg, lo que es rápido para muchas aplicaciones. La corriente luego se difunde en el conductor donde la densidad de corriente se obtiene fácilmente de la ley de Ampere como

\[\begin{align*}  \textbf{J}_{f} &= \nabla \times \textbf{H} \\[4pt] &= - \dfrac{\partial H_{z}}{\partial x} \textbf{i}_{y} \\[4pt] &= \dfrac{I}{Dd} \bigg( 1 + 2 \sum_{n=1}^{\infty} \cos \dfrac{n \pi x}{d} e^{n^{2} t/\tau} \bigg) \textbf{i}_{y} \end{align*} \nonumber \]

La difusión del campo magnético y la densidad de corriente se representan gráficamente en la Figura 6-26b para varios tiempos

La fuerza sobre la losa conductora se debe a la fuerza de Lorentz que tiende a expandir el bucle y a una fuerza de magnetización debido a la diferencia de permeabilidad de la losa y el espacio libre circundante como se deriva en la Sección 5-8-1:

\[\begin{align*} \textbf{F} &= \mu_{0} (\textbf{M} \cdot \nabla) \textbf{H} + \mu_{0} \textbf{J}_{f} \times \textbf{H} \\[4pt] &= ( \mu - \mu_{0})(\textbf{H} \cdot \nabla) \textbf{H} + \mu_{0} \textbf{J}_{f} \times \textbf{H} \end{align*} \nonumber \]

Para nuestro caso con\(\textbf{H} = H_{z} (x) \textbf{i}_{z}\), la densidad de fuerza de magnetización no tiene ninguna contribución por lo que (30) reduce a

\[\begin{align*} \textbf{F} &= \mu_{0} (\nabla \times \textbf{H}) \times \textbf{H} \\[4pt] &= \mu_{0} (\textbf{H} \cdot \nabla ) \textbf{H} - \nabla (\dfrac{1}{2} \mu_{0} \textbf{H} \cdot \textbf{H}) \\[4pt] &= - \dfrac{d}{dx} (\dfrac{1}{2} \mu_{0} H^{2}_{z}) \textbf{i}_{x} \end{align*} \nonumber \]

Integrando (31) sobre el volumen de la losa con el campo magnético independiente de y y z,

\[\begin{align*} f_{x} &= - \int_{0}^{d} s D \dfrac{d}{dx} \left(\dfrac{1}{2} \mu_{0}H_{z}^{2}\right) dx \\[4pt] &= - \dfrac{1}{2} \mu_{0} H_{z}^{2} s D \big|_{0}^{d} \\[4pt] &= \dfrac{1}{2} \dfrac{\mu_{0} I^{2}s}{D} \end{align*} \nonumber \]

nos da una fuerza constante con el tiempo que es independiente de la permeabilidad. Nótese que nuestro enfoque de expresar la densidad de corriente en términos del campo magnético en (31) fue más fácil que multiplicar las series infinitas de (27) y (29), ya que el resultado entonces solo dependía del campo magnético en los límites que se conocen a partir de las condiciones límite de (20). La integración resultante en (32) fue fácil porque la densidad de fuerza en (31) se expresó como un derivado puro de x.

6-4-4 El estado estacionario sinusoidal (profundidad de la piel)

Ahora colocamos una losa conductora infinitamente gruesa a una distancia d por encima de una lámina de corriente sinusoidalmente variable\(K_{0} \cos \omega t \textbf{i}_{y}\), que se encuentra encima de un conductor perfecto, como en la Figura 6-27a. El

Figura 6-27 (a) Un conductor estacionario se encuentra por encima de una corriente superficial sinusoidal colocada sobre un conductor perfecto de manera que H = 0 para\(x < -d\). (b) El campo magnético y la densidad de corriente se propaga y decae en el conductor con la misma longitud característica dada por la profundidad de la piel\(\delta = \sqrt{2/(\omega \mu \sigma)} \) La velocidad de fase de la onda es\(\omega \delta\).

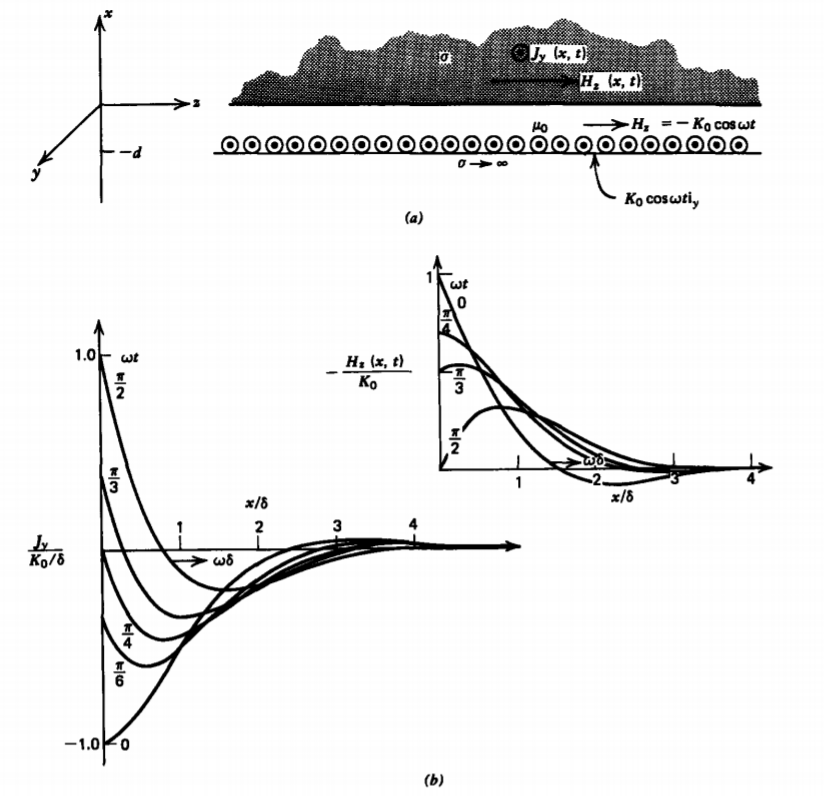
campo magnético dentro del conductor es entonces también sinusoidalmente variable con el tiempo:

\[H_{z} (x,t) \textrm{Re} [ \hat{H}_{z} (x) e^{j \omega t} ] \nonumber \]

Sustituyendo (33) en (14) rendimientos

\[\dfrac{d^{2} \hat{H}_{z}}{dx^{2}} - j \omega \mu \sigma \hat{H}_{z} = 0 \nonumber \]

con solución

\[\hat{H}_{z} (x) = A_{1} e^{(1 + j)x/\delta} + A_{2} e^{-(1 + j) x/\delta} \nonumber \]

donde la profundidad de la piel\(\delta\) se define como

\[\delta = \sqrt{2/(\omega \mu \sigma)} \nonumber \]

Dado que el campo magnético debe permanecer finito lejos de la hoja actual,\(A_{1}\) debe ser cero. El campo magnético también es continuo a través del límite x =0 porque no hay corriente superficial, por lo que la solución es

\[H_{z} (x,t) = \textrm{Re} [- K_{0} e^{-(1 + j) x/\delta} e^{j \omega t} ] \\ = - K_{0} \cos (\omega t - x/\delta) e^{-x/\delta}, \: \: \: x \geq 0 \nonumber \]

donde el campo magnético en el hueco es uniforme, determinado por la discontinuidad en H tangencial\(x = -d\) a ser\(H_{z} = -K_{y}\) para\(-d < x \leq 0\) desde dentro del conductor perfecto\((x < -d \textbf{H} = 0\). El campo magnético se difunde en el conductor como una onda de propagación fuertemente amortiguada con profundidad de penetración característica\(\delta\). La profundidad de la piel también\(\delta\) es igual a la longitud de onda de propagación, como se dibuja en la Figura 6-27b. La densidad de corriente dentro del conductor

\[\text{J}_{f} = \nabla \times \textbf{H} = - \dfrac{\partial H_{z}}{\partial x} \textbf{i}_{y} \\ = + \dfrac{K_{0} e^{-x/\delta}}{\delta} \bigg[ \sin \bigg( \omega t - \dfrac{x}{\delta} \bigg) - \cos \bigg( \omega t - \dfrac{x}{\delta} \bigg) \bigg] \textbf{i}_{y} \nonumber \]

también se dibuja en la Figura 6-27b en diversos momentos del ciclo, estando confinado cerca de la interfaz a una profundidad del orden de\(\delta\). Para un conductor perfecto,\(\delta \rightarrow 0\), y la corriente de volumen se convierte en una corriente superficial.

El agua de mar tiene una conductividad de\( \approx 4\) siemens/m de manera que a una frecuencia de\(f\) = 1 MHz (\( \omega = 2 \pi f\)) la profundidad de la piel es\( \delta \approx 0.25\). Es por ello que las comunicaciones por radio a los submarinos son difíciles. La conductividad del cobre es\(\sigma \approx 6 \times 10^{7}\) siemens/m de manera que a 60 Hz la profundidad de la piel es\(\delta \approx 8\) mm. Los cables de alimentación con radios más grandes tienen la mayor parte de la corriente confinada cerca de la superficie de modo que el núcleo central transporta muy poca corriente. Esto reduce el área de la sección transversal a través de la cual fluye la corriente, elevando la resistencia del cable conduciendo a una mayor disipación de potencia

Nuevamente, la densidad de fuerza de magnetización no contribuye a la densidad de fuerza ya que\(H_{z}\) solo depende de x:

\[\textbf{F} = \mu_{0} (\textbf{M} \cdot \nabla) \textbf{H} + \mu_{0} \textbf{J}_{f} \times \textbf{H}\\ = \mu_{0} (\nabla \times \textbf{H}) \times \textbf{H} \\ = - \nabla (\dfrac{1}{2} \mu_{0} \textbf{H} \cdot \textbf{H}) \nonumber \]

La fuerza total por unidad de área sobre la losa obtenida al integrar (39) sobre x depende únicamente del campo magnético a x = 0:

\[f_{x} = - \int_{0}^{\infty} \dfrac{d}{dx} \bigg( \dfrac{\mu_{0}}{2} H_{z}^{2} \bigg) dx \\ = - \dfrac{1}{2} \mu_{0} H_{z}^{2} \big|_{0}^{\infty} \\ = \dfrac{1}{2} \mu_{)} K_{0}^{2} \cos^{2} \omega t \nonumber \]

porque nuevamente H es independiente de y y z y el componente x de la densidad de fuerza de (39) fue escrito como una derivada pura con respecto a x. Obsérvese que este enfoque fue más fácil que integrar el producto cruzado de (38) con (37).

Esta fuerza se puede utilizar para levitar el conductor. Tenga en cuenta que la región para\(x > \delta\) es peso muerto, ya que aporta muy poco a la fuerza magnética.

*\(\int_{0}^{d} (d-x) \sin \dfrac{m \pi x}{d} dx = \dfrac{d^{2}}{m \pi}\)

6-4-5 Efectos de la Convección

Una corriente superficial dc distribuida\(-K_{0} \textbf{i}_{y}\) a x =0 fluye a lo largo de electrodos paralelos y regresa a través de un fluido conductor que se mueve hacia la derecha con velocidad constante\(v_{0} \textbf{i}_{x}\), como se muestra en la Figura 6-28a. El flujo no se ve obstaculizado por la fuente de corriente a x = 0. Con el descuido de la franja, el campo magnético es puramente z dirigido y solo depende de la coordenada x, de manera que (13) en el estado estacionario dc, con\(\textbf{U} = v_{0} \textbf{i}_{x}\) ser una constante, se convierte*

\[\dfrac{d^{2}H_{z}}{dx^{2}} - \mu \sigma v_{0} \dfrac{dH_{z}}{dx} = 0 \nonumber \]

Soluciones de la forma

\[H_{z} (x) = A e^{px} \nonumber \]

Figura 6-28 (a) Un material conductor que se mueve a través de un campo magnético tiende a tirar del campo magnético y la densidad de corriente con él. (b) El campo magnético y la densidad de corriente se ven muy perturbados por el flujo cuando el número magnético de Reynolds es grande,\(R_{m} = \sigma \mu Ul >>1\).

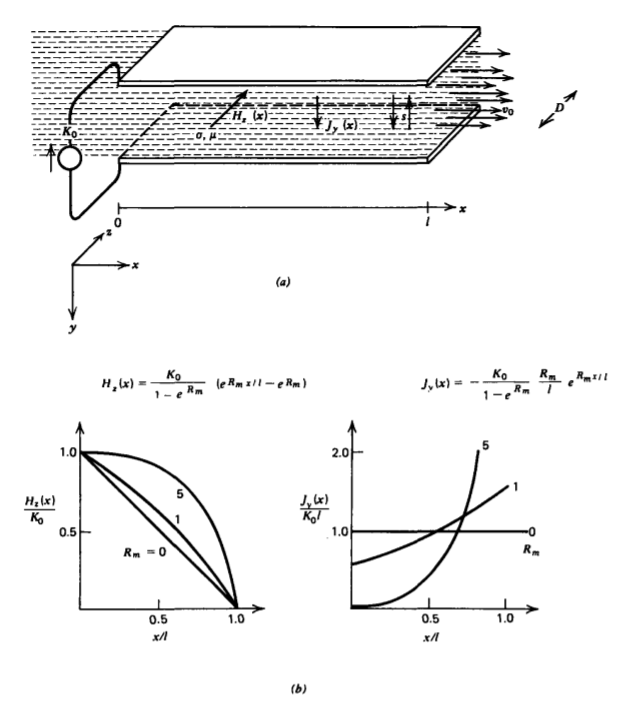
cuando se vuelve a sustituir en (41) producen dos valores permitidos de p,

\[p^{2} - \mu \sigma v_{0} p = 0 \Rightarrow p = 0, \: \: \: \: p = \mu \sigma v_{0} \nonumber \]

Dado que (41) es lineal, la solución más general es solo la suma de las dos soluciones permitidas,

\[H_{z} (x) = A_{1} e^{R_{m} x/l} + A_{2} \nonumber \]

donde el número magnético de Reynold se define como

\[R_{m} = \sigma \mu v_{0} l = \dfrac{\sigma \mu l^{2}}{l/v_{0}} \nonumber \]

y representa la relación de un tiempo de difusión magnética representativo dado por (28) a un tiempo de transporte de fluido (\(l/v_{0}\)). Las condiciones de contorno son

\[H_{z} (x=0) = K_{0}, \: \: \: \: H_{z}(x=l) = 0 \nonumber \]

para que la solución sea

\[H_{z} (x) = \dfrac{K_{0}}{1-e^{R_{m}}} (e^{R_{m}x/l} - e^{R_{m}}) \nonumber \]

La distribución de corriente asociada es entonces

\[\textbf{J}_{f} = \nabla \times \textbf{H} = - \dfrac{\partial H_{z}}{\partial x} \textbf{i}_{y} \\ = - \dfrac{K_{0}}{1-e^{R_{m}}} \dfrac{R_{m}}{l} e^{R_{m}x/l} \textbf{i}_{y} \nonumber \]

Las distribuciones de campo y corriente trazadas en la Figura 6-28b para varios\(R_{m}\) muestran que el campo magnético y la corriente son arrastrados a lo largo en la dirección del flujo. Para pequeños\(R_{m}\) el campo magnético apenas se ve perturbado por la solución de flujo cero de un campo lineal y distribución de corriente constante. Para muy grandes\(R_{m} >> 1\), el campo magnético se acerca a una distribución uniforme mientras que la densidad de corriente se acerca a una corriente superficial en\(x = l\).

La fuerza sobre el fluido en movimiento es independiente de la velocidad del flujo:

\[\textbf{f} = \int_{0}^{l} \textbf{J} \times \mu_{0} \textbf{H} s D \: dx \\ = - \dfrac{K_{0}^{2}}{(1 - e^{R_{m}})^{2}} \mu_{0} \dfrac{R_{m}}{l} sD \int_{0}^{l} e^{R_{m}x/l}(e^{R_{m}x/l}-e^{R_{m}}) dx \: \textbf{i}_{x} \\ = - \dfrac{K_{0}^{2} \mu_{0} sD}{(1-e^{R_{m}})^{2}} e^{R_{m}x/l} \bigg( \dfrac{e^{R_{m}x/l}}{2} - e^{R_{m}} \bigg) \bigg|_{0}^{l} \textbf{i}_{x} \\ = \dfrac{1}{2} \mu_{0} K_{0}^{2} s D \textbf{i}_{x} \nonumber \]

*\(\nabla \times (\textbf{U} \times \textbf{H}) = \textbf{U} (\nabla \cancelto{0}{\cdot} \textbf{H}) - \textbf{H}(\nabla \cancelto{0}{\cdot} \textbf{U}) + (\textbf{H} \cancelto{0}{\cdot} \nabla) \textbf{U} - (\textbf{U} \cdot \nabla) \textbf{H} = - v_{0} \dfrac{d \textbf{H}}{dx}\)

6-4-6 A Máquina de Inducción Lineal

Las corrientes inducidas en un conductor debido a un campo magnético variable en el tiempo dan lugar a una fuerza que puede hacer que el conductor se mueva. Esto describe un motor. El efecto inverso es cuando hacemos que un conductor se mueva a través de un campo magnético variable en el tiempo generando una corriente, que describe un generador.

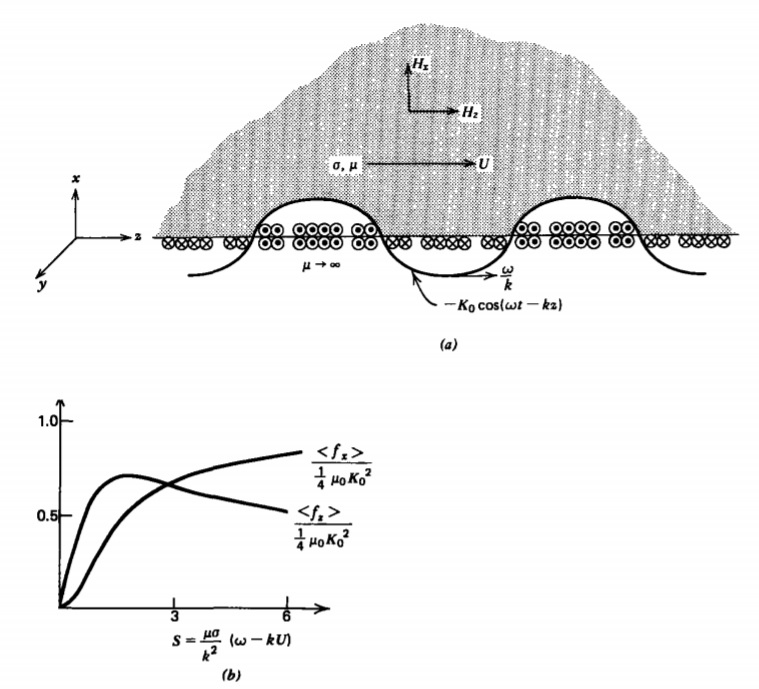
La máquina de inducción lineal mostrada en la Figura 6-29a asume que un conductor se mueve hacia la derecha a velocidad constante\(U \textbf{i}_{z}\). Directamente debajo del conductor sin espacio hay una corriente superficial colocada encima de un medio infinitamente permeable

\[\textbf{K} (t) = -K_{0} \cos (\omega t- kz) \textbf{i}_{y} = \textrm{Re} [ - K_{0} e^{j(\omega t - kz)} \textbf{i}_{y}] \nonumber \]

que es una ola viajera que se mueve hacia la derecha a velocidad\(\omega /k\). Para x >0, el campo magnético tendrá entonces componentes x y z de la forma

\[H_{z}(x, z, t) = \textrm{Re} [ \hat{H}_{z} (x) e^{j (\omega t- kz)}] \\ H_{x} (x, z, t) = \textrm{Re} [\hat{H}_{x} (x) e^{j(\omega t - kz)}] \nonumber \]

Figura 6-29 (a) Una onda viajera de corriente superficial induce corrientes en un conductor que se mueve a una velocidad U diferente de la velocidad de la onda\(\omega/k\). (b) Las fuerzas resultantes pueden levitar e impulsar el conductor en función del deslizamiento S, que mide la diferencia de velocidades del conductor y la onda viajera.

donde (10) (\(\nabla \cdot \textbf{B} = 0\)) requiere que estos componentes estén relacionados como

\[\dfrac{d \hat{H}_{x}}{dx} - jk \hat{H}_{z} =0 \nonumber \]

El componente z de la ecuación de difusión magnética de (13) es

\[\dfrac{d^{2} \hat{H}_{z}}{d x^{2}} - k^{2} \hat{H}_{2} = j \mu \sigma (\omega - k U) \hat{H}_{z} \nonumber \]

que también se puede escribir como

\[\dfrac{d^{2}\hat{H}_{z}}{dx^{2}} - \gamma^{2} \hat{H}_{z} =0 \nonumber \]

donde

\[\gamma^{2} = k^{2} (1 + jS), \: \: \: \: S = \dfrac{\mu \sigma}{k^{2}} (\omega - kU) \nonumber \]

y S se conoce como el resbalón. Las soluciones de (54) vuelven a ser exponenciales pero complejas porque\(\gamma\) son complejas:

\[\hat{H}_{z} = A_{1} e^{\gamma x} + A_{2} e^{-\gamma x} \nonumber \]

Porque\(\hat{H}_{z}\) debe permanecer finito lejos de la hoja actual,\(A_{1} = 0\), de manera que usando (52) el campo magnético es de la forma

\[\hat{\textbf{H}} = K_{0} e^{- \gamma x} \bigg( \textbf{i}_{z} - \dfrac{jk}{\gamma} \textbf{i}_{x} \bigg) \nonumber \]

donde utilizamos el hecho de que el componente tangencial de H es discontinuo en la corriente superficial, con H = 0 para x <0.

La densidad de corriente en el conductor es

\[\textbf{J}_{f} = \nabla \times \textbf{H} = \textbf{i}_{y} \bigg( \dfrac{\partial H_{x}}{\partial z} - \dfrac{\partial H_{z}}{\partial x} \bigg) \Rightarrow \hat{J}_{y} = -jk \hat{H}_{x} - \dfrac{d \hat{H}_{z}}{dx} \\ = K_{0} e^{- \gamma x} \dfrac{(\gamma^{2} - k^{2})}{\gamma} \\ = \dfrac{K_{0}k^{2}jS e^{-\gamma x}}{\gamma} \nonumber \]

Si el conductor y la onda de corriente viajan a la misma velocidad (\(\omega/k = U\)), no se induce corriente ya que el deslizamiento es cero. Las corrientes solo se inducen si el conductor y la onda viajan a diferentes velocidades. Este es el principio de todas las máquinas de inducción.

La fuerza por unidad de área en el conductor tiene entonces componentes x y z:

\[\textbf{f} = \int_{0}^{\infty} \textbf{J} \times \mu_{0} \textbf{H} dx \\ = \int_{0}^{\infty} \mu_{0} J_{y} (H_{z} \textbf{i}_{x} - H_{x} \textbf{i}_{z}) dx \nonumber \]

Estas integraciones son sencillas pero largas porque primero se debe encontrar el campo instantáneo y la densidad de corriente a partir de (51) tomando las partes reales. Más importante es la fuerza promedio en el tiempo por unidad de área durante un período de excitación

\[< \textbf{f} > = \dfrac{\omega}{2 \pi} \int_{0}^{2 \pi/ \omega} \textbf{f} dt \nonumber \]

Dado que la parte real de una cantidad compleja es igual a la mitad de la suma de la cantidad y su complejo conjugado,

\[A = \textrm{Re}[\hat{A} e^{j \omega t}] = \dfrac{1}{2} (\hat{A} e^{j \omega t} + \hat{A}* e^{-j \omega t}) \\ B = \textrm{Re} [\hat{B} e^{j \omega t}] = \dfrac{1}{2} (\hat{B} e^{j \omega t} + \hat{B}* e^{-j \omega t}) \nonumber \]

el producto promedio en el tiempo de dos cantidades es

\[\dfrac{\omega}{2 \pi} \int_{0}^{2 \pi/\omega} AB dt = \dfrac{1}{4} \dfrac{\omega}{2 \pi} \int_{0}^{2 \pi/\omega} (\hat{A} \hat{B} e^{2 j \omega t} + \hat{A} * \hat{B} + \hat{A} \hat{B} * \\ + \hat{A} * \hat{B}* e^{-2 j \omega t}) dt \\ = \dfrac{1}{4} (\hat{A} * \hat{B} + \hat{A} \hat{B} *) \\ \hat{1}{2} \textrm{Re} (\hat{A} \hat{B} *) \nonumber \]

que es una fórmula utilizada a menudo para la potencia promedio en el tiempo en circuitos donde A y B son el voltaje y la corriente.

Luego usando (62) en (59), el componente x de la fuerza promedio en el tiempo por unidad de área es

\[ <f_{x}> = \dfrac{1}{2} \textrm{Re} \bigg( \int_{0}^{\infty} \mu_{0} \hat{J}_{y} \hat{H}_{z} * dx \bigg) \\ = \dfrac{\mu_{0}}{2} K_{0}^{2} k^{2} S \textrm{Re} \bigg( \dfrac{j}{\gamma} \int_{0}^{\infty} e^{- (\gamma + \gamma * ) x} dx \bigg) \\ = \dfrac{\mu_{0}}{2} K_{0}^{2} k^{2} S \textrm{Re} \bigg( \dfrac{j}{\gamma (\gamma + \gamma *)} \bigg) \\ = \dfrac{1}{4} \dfrac{\mu_{0}K_{0}^{2}S^{2}}{[1 + S^{2} + (1 + S^{2})^{1/2}]} = \dfrac{1}{4} \mu_{0}K_{0}^{2} \bigg( \dfrac{\sqrt{1 + S^{2}} -1}{\sqrt{1 + S^{2}}} \bigg) \nonumber \]

donde se evaluaron las últimas igualdades en términos del deslizamiento S de (55).

De manera similar calculamos la fuerza de corte promedio en el tiempo por unidad de área como

\[< f_{z} > = - \dfrac{1}{2} \textrm{Re} \bigg( \int_{0}^{\infty} \mu_{0} J_{y} H*_{x} dx \bigg) \\ = \dfrac{\mu_{0}}{2} \dfrac{K_{0}^{2} k^{3} S}{\gamma \gamma*} \textrm{Re} \bigg( \int_{0}^{\infty} e^{- (\gamma + \gamma*)x} dx \bigg) \\ = \dfrac{\mu_{0}}{2} \dfrac{k^{3} K_{0}^{2}S}{\gamma \gamma*} \textrm{Re} \bigg( \dfrac{1}{(\gamma + \gamma*)} \bigg) \\ = \dfrac{\mu_{0}K_{0}^{2}S}{4 \sqrt{1 + S^{2}} \textrm{Re} ( \sqrt{1 + jS})} \nonumber \]

Cuando la velocidad de la onda excede la velocidad del conductor (\(\omega/k > U\)), la fuerza es positiva como S >0 de modo que la onda tira del conductor a lo largo. Cuando S < 0, la onda lenta tiende a tirar del conductor hacia atrás como\(<f_{z}> < 0\). Las fuerzas de (63) y (64), trazadas en la Figura 6-29b, se pueden utilizar para levantar e impulsar simultáneamente un material conductor. No hay fuerza cuando la onda y el conductor viajan a la misma velocidad (\(\omega/k = U\)) que el deslizamiento es cero (\(S = 0\)). Para S grandes, la fuerza de levitar\(<f_{x}>\) se aproxima al valor constante\(\dfrac{1}{4} \mu_{0}K_{0}^{2}\) mientras que la fuerza de cizallamiento se aproxima a cero. Hay un valor óptimo de S que maximiza\(< f_{z}>\). Para S más pequeños, se induce menos corriente mientras que para S más grandes la diferencia de fase entre las corrientes impuestas e inducidas tienden a disminuir la fuerza promedio en el tiempo.

6-4-7 Superconductores

En el límite de la conductividad óhmica infinita (\(\sigma \rightarrow \infty\)), la constante de tiempo de difusión de (28) se vuelve infinita mientras que la profundidad de la piel de (36) se vuelve cero. El campo magnético no puede penetrar un conductor perfecto y las corrientes están completamente confinadas a la superficie.

Sin embargo, en este límite la ley de conducción óhmica ya no es válida y debemos usar la ley constitutiva superconductora desarrollada en la Sección 3-2-2d para un solo portador de carga:

\[\dfrac{\partial \textbf{J}}{\partial t} = \omega_{p}^{2} \varepsilon \textbf{E} \nonumber \]

Luego para un medio estacionario, siguiendo el mismo procedimiento que en (12) y (13) con la ley constitutiva de (65), (8) - (11) reducir a

\[\nabla^{2} \dfrac{\partial \textbf{H}}{\partial t} - \omega^{2}_{p} \varepsilon \mu \dfrac{\partial \textbf{H}}{\partial t} = 0 \Rightarrow \nabla^{2} (\textbf{H} - \textbf{H}_{0}) - \omega^{2}_{p} \varepsilon \mu (\textbf{H}-\textbf{H}_0}) = 0 \nonumber \]

donde\(\textbf{H}_{0}\) esta el campo magnetico instantaneo en\(t =0\). Si el material superconductor no tiene campo magnético inicial cuando se enciende por primera vez una excitación, entonces\(\textbf{H}_{0} = 0\).

Si la losa conductora en la Figura 6-27a se convierte en superconductora, (66) se convierte en

\[\dfrac{d^{2}H_{z}}{dx^{2}} - \dfrac{\omega_{p}^{2}}{c^{2}}H_{z} = 0, \: \: \: c = \dfrac{1}{\sqrt{\varepsilon \mu}} \nonumber \]

donde c es la velocidad de la luz en el medio.

La solución a (67) es

\[H_{z} = A_{1} e^{\omega_{p} x/c} + A_{2} e^{- \omega_{p} x/c} \\ = - K_{0} \cos \omega t \: e^{-\omega_{0} x/c} \nonumber \]

donde usamos la condición límite de continuidad de H tangencial a x = 0.

La densidad de corriente es entonces

\[J_{y} = - \dfrac{\partial H_{z}}{\partial x} \\ = - \dfrac{K_{0} \omega_{p}}{c} \cos \omega t e^{- \omega_{p} x/c} \nonumber \]

Para cualquier frecuencia\(\omega\), incluyendo dc (\(\omega\)= 0), el campo y la corriente decaen con longitud característica:

\[l_{c} = c/\omega_{p} \nonumber \]

Dado que la frecuencia del plasma\(\omega_{p}\) es típicamente del orden de 10 ¹⁵ radianes/seg, esta longitud característica es muy pequeña,\(l_{c} \approx 3 \times 10^{8} / 10^{15} \approx 3 \times 10^{-7}\) m. A excepción de esta delgada vaina, el campo magnético se excluye del superconductor mientras que la corriente de volumen se limita a esta región cercana a la interfaz.

Hay una excepción experimental a la ecuación gobernante en (66), conocida como el efecto Meissner. Si un conductor ordinario se coloca dentro de un campo magnético de CC H ₀ y luego se enfría a través de la temperatura de transición para superconductividad, el flujo magnético es empujado hacia afuera excepto por una vaina delgada de ancho dada por (70). Esto es contrario a (66), que permite la solución independiente del tiempo H = H ₀, donde el campo magnético permanece atrapado dentro del superconductor. Aunque la razón no se entiende bien, los superconductores se comportan como si H ₀ =0 no importa cuál sea el valor inicial del campo magnético.