6.6: El método energético para las fuerzas
- Page ID
- 86765
El principio del trabajo virtual
En la Sección 6-5-1 calculamos la energía almacenada en un bucle portador de corriente por dos métodos. Primero calculamos la entrada de energía eléctrica a un bucle sin trabajo mecánico realizado. Luego obtuvimos la misma respuesta calculando el trabajo mecánico necesario para mover un bucle portador de corriente en un campo externo sin más entradas eléctricas. En el caso más general, una entrada de energía eléctrica puede resultar en energía almacenada dW y trabajo mecánico por la acción de una fuerza\(f_{x}\) que provoca un pequeño desplazamiento dx:
\[i d \Phi = d W + f_{x} dx \nonumber \]
Si conociéramos la energía total almacenada en el campo magnético en función del flujo y la posición, la fuerza simplemente se encuentra como
\[f_{x} = - \frac{\partial W}{\partial x} \bigg|_{\Phi} \nonumber \]
Podemos calcular fácilmente la energía almacenada al darnos cuenta de que no importa por qué proceso u orden se ensamble el sistema, si la posición final x y el flujo\(\Phi\) son iguales, la energía es la misma. Dado que la energía almacenada es independiente del orden en que aplicamos entradas mecánicas y eléctricas, elegimos ensamblar mecánicamente un sistema primero a su posición final x sin excitaciones eléctricas para que\(\Phi = 0\). Esto no requiere trabajo ya que con flujo cero no hay fuerza de origen eléctrico. Una vez que el sistema está ensamblado mecánicamente para que su posición permanezca constante, aplicamos la excitación eléctrica para llevar el sistema a su valor de flujo final. La energía eléctrica requerida es
\[W = \int_{x \textrm{ const}} i d \Phi \nonumber \]
Para materiales lineales, el flujo y la corriente están linealmente relacionados a través de la inductancia que ahora puede ser una función de x porque la inductancia depende de la geometría:
\[i = \Phi/L (x) \nonumber \]
El uso de (4) en (3) nos permite tomar la inductancia fuera de la integral porque x se mantiene constante para que la inductancia también sea constante:
\[W = \frac{1}{L(x)} \int_{0}^{\Phi} \Phi d \Phi \\ = \frac{\Phi^{2}}{2 L (x)} = \frac{1}{2} L (x) i^{2} \nonumber \]
La energía almacenada es la misma que se encuentra en la Sección 6-5-2 incluso cuando se incluye trabajo mecánico y la inductancia varía con la posición.
Para encontrar la fuerza sobre el miembro móvil, utilizamos (2) con la expresión de energía en (5), que depende únicamente del flujo y la posición:
\[f_{x} = - \frac{\partial W}{\partial x} \bigg|_{\Phi} \\ = - \frac{\Phi^{2}}{2} \frac{d [1/L(x)]}{dx} \\ = \frac{1}{2} \frac{\Phi^{2}}{L^{2}(x)} \frac{dL(x)}{dx} \\ = \frac{1}{2} i^{2} \frac{dL(x)}{dx} \nonumber \]
Mirador de Circuito
Este resultado también se puede obtener usando una descripción de circuito con la relación flujo-corriente lineal de (4):
\[v = \frac{d \Phi}{dt} = L (x) \frac{di}{dt} + i \frac{dL(x)}{dt} \\ = L (x) \frac{di}{dt} + i \frac{dL(x)}{dx} \frac{dx}{dt} \nonumber \]
El último término, proporcional a la velocidad del miembro móvil, solo se suma al término de voltaje inductivo habitual. Si la geometría es fija y no cambia con el tiempo, no hay término de acoplamiento electromecánico.
La potencia entregada al sistema es
\[p = vi = i \frac{d}{dt} [L(x)i] \nonumber \]
que se puede ampliar como
\[p = \frac{d}{dt}(\frac{1}{2}L(x)i^{2}) + \frac{1}{2}i^{2} \frac{dL(x)}{dx} \frac{dx}{dt} \nonumber \]
Esto está en la forma
\[p = \frac{dW}{dt} + f_{x} \frac{dx}{dt}, \: \left \{ \begin{matrix} W = \frac{1}{2} L (x) i^{2} \\ f_{x} = \frac{1}{2} i^{2} \frac{dL(x)}{dx} \end{matrix} \right. \nonumber \]
que establece que la potencia entregada al inductor es igual a la suma de la tasa de tiempo de energía. potencia almacenada y mecánica realizada en el inductor. Esto concuerda con el enfoque del método energético. Si la inductancia no cambia con el tiempo debido a que la geometría es fija, se almacena toda la potencia de entrada. como energía potencial\(W\).
(a) Relé
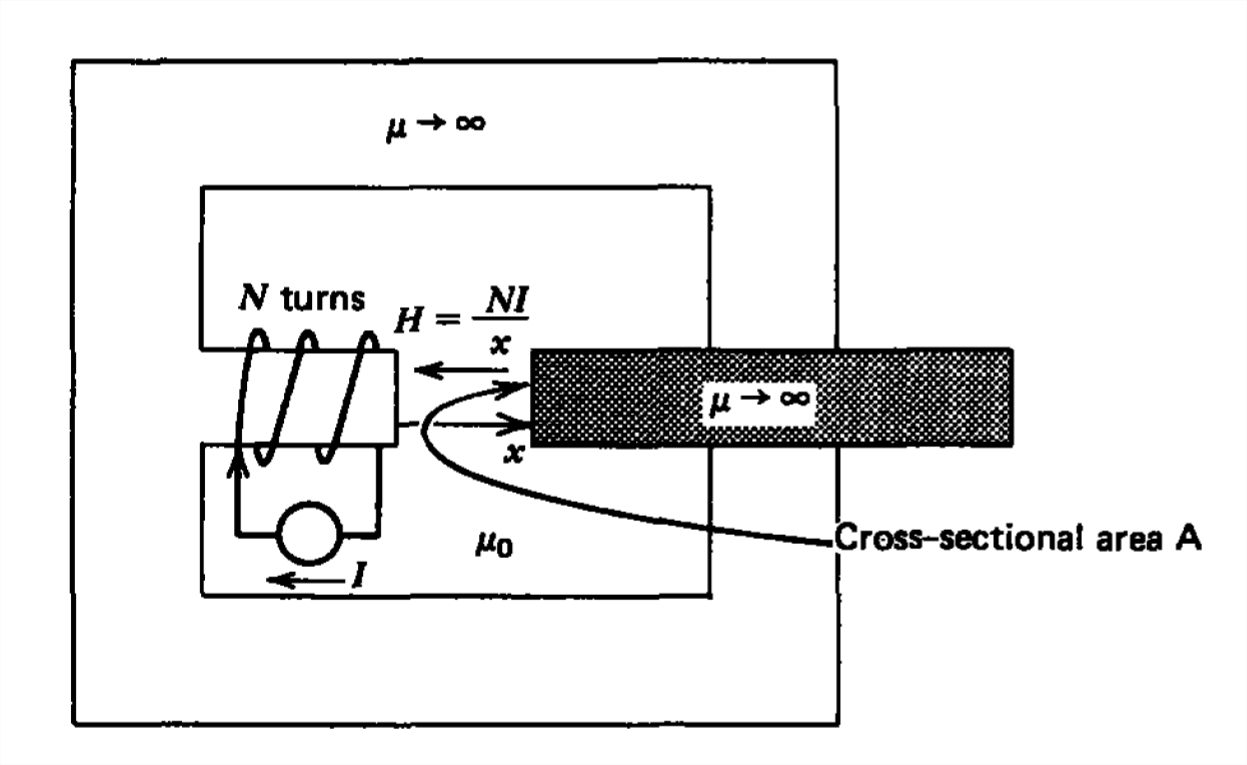
Encuentra la fuerza sobre el slug móvil en el circuito magnético que se muestra en la Figura 6-34.
SOLUCIÓN
Es necesario encontrar la inductancia del sistema en función de la posición de la babosa para que podamos usar (6). Debido al núcleo y la babosa infinitamente permeables, el\(\textbf{H}\) campo es distinto de cero solo en el espacio de aire de longitud\(x\). Utilizamos la ley de Ampere para obtener
\(H=NI/x\)
El flujo a través de la brecha
\(\Phi =\mu _{0}NIA/x\)
es igual al flujo a través de cada vuelta de la bobina que produce la inductancia como
\(L\left ( x \right )=\frac{N\Phi }{I}=\frac{\mu _{0}N^{2}A}{x}\)
La fuerza es entonces
\(\begin{align} f_{x}&=\frac{1}{2}I^{2}\frac{dL\left (x \right )}{dx}\nonumber \\ &=-\frac{\mu _{0}N^{2}AI^{2}}{2x^{2}}\end{align}\)
El signo menos significa que la fuerza es opuesta a la dirección de aumento\(x\), de manera que la pieza móvil es atraída hacia la bobina.
(b) Bucle de una vuelta
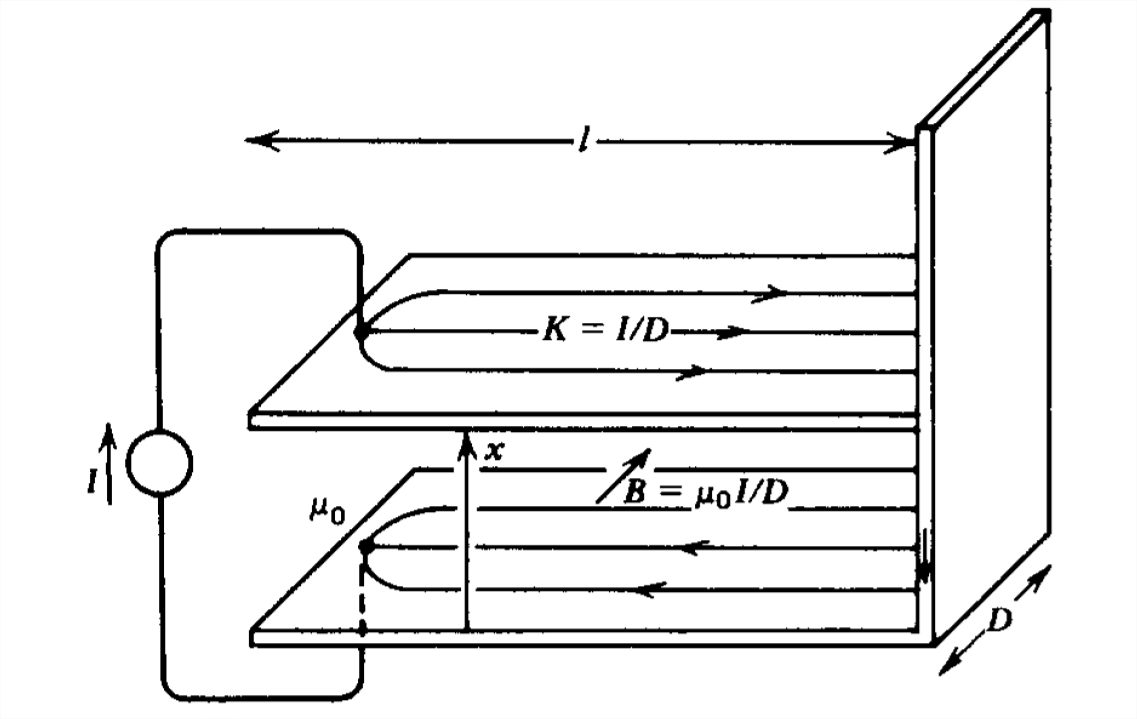
Encuentra la fuerza sobre la placa superior móvil en el bucle de una vuelta que se muestra en la Figura 6-35.
SOLUCIÓN
La corriente se distribuye uniformemente como una corriente superficial\(K=I/D\) en la placa móvil. Si descuidamos los efectos de campo no uniformes cerca de las esquinas, el\(\textbf{H}\) campo que es tangente a los conductores es igual a\(K\):
\(H_{z}=I/D\)
El flujo total vinculado por la fuente de corriente es entonces
\(\begin{align}\Phi &=\mu _{0}H_{z}xl\nonumber \\ &=\frac{\mu _{0}xl}{D}I\end{align}\)
que da la inductancia como
\(L\left ( x \right )=\frac{\Phi }{I}=\frac{\mu _{0}xl}{D}\)
La fuerza es entonces constante
\(\begin{align} f_{x}&=\frac{1}{2}I^{2}\frac{dL\left (x \right )}{dx}\nonumber \\ &=\frac{1}{2}\frac{\mu _{0}lI^{2}}{D}\end{align}\)
Fuerza de magnetización
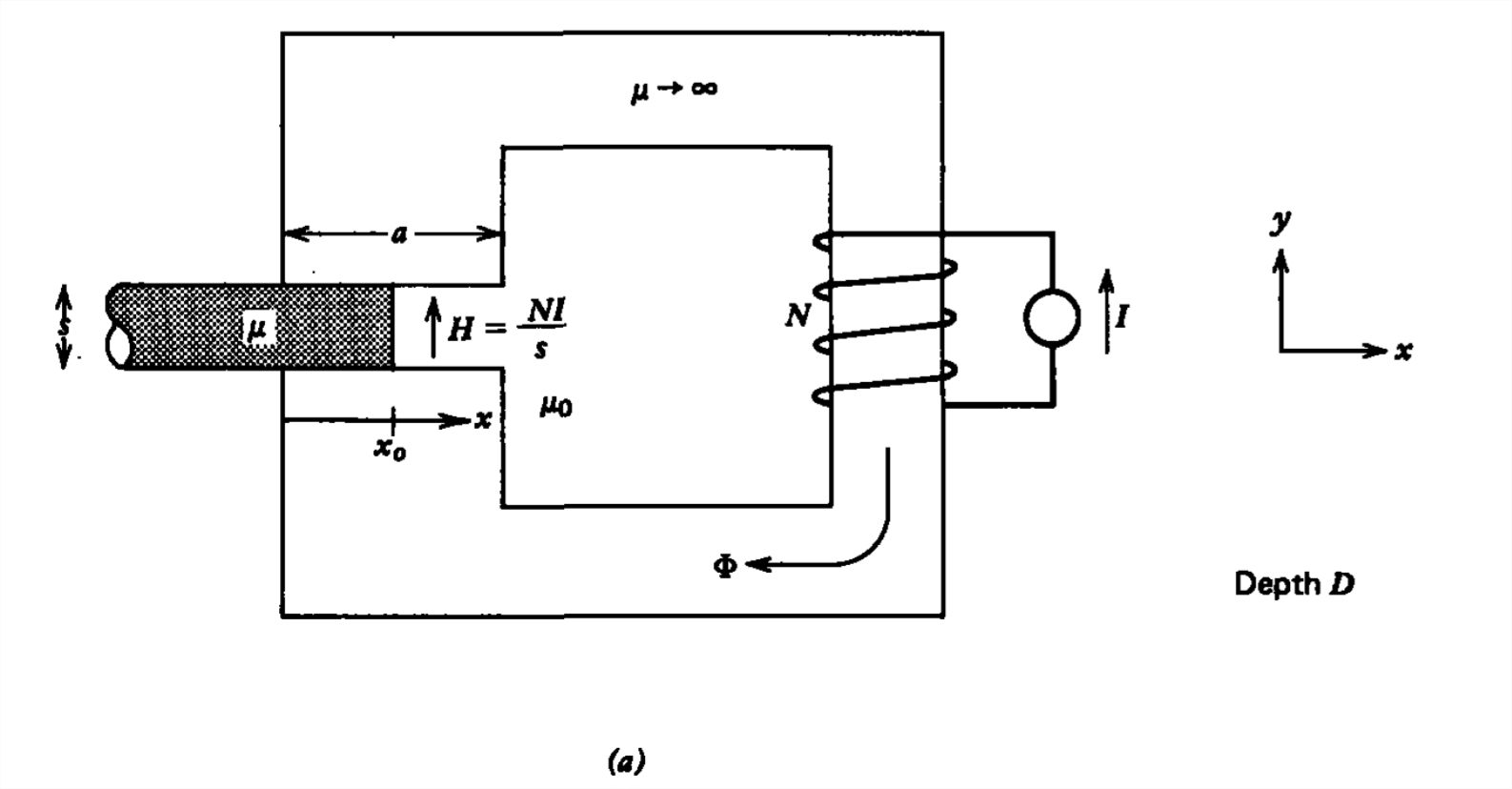
Un material con permeabilidad\(\mu \) se inserta parcialmente en el circuito magnético mostrado en la Figura 6-36. Sin corriente libre en el material móvil, la densidad\(x\) de fuerza dirigida de la Sección 5-8-1 es
\ [\ begin {align} F_ {x} &=\ mu _ {0}\ izquierda (\ textbf {M}\ cdot\ nabla\ derecha) H_ {x}\ nonumber\\ &
=\ izquierda (\ mu -\ mu _ {0}\ derecha)\ izquierda (\ textbf {H}\ cdot\ nabla\ derecha) H_ {x}\ nonumbla er\\ &
=\ izquierda (\ mu -\ mu _ {0}\ derecha)\ izquierda (H_ {x}\ frac {\ parcial H_ {x}} {\ parcial x} +H_ {y}\ frac {\ parcial H_ {x}} {\ parcial y}\ derecha)\ end {align}\ nonumber\]
donde descuidamos las variaciones con\(z\). Esta fuerza surge en el campo de franjas porque dentro del espacio el campo magnético es esencialmente uniforme:
\[H_{y}=NI/s \nonumber \]
Debido a que el campo magnético en el bloque permeable está libre de rizos,
\[\nabla \times \textbf{H}=0\Rightarrow \frac{\partial H_{x}}{\partial y}=\frac{\partial H_{y}}{\partial x} \nonumber \]
(11) se puede reescribir como
\[F_{x}=\frac{\left ( \mu -\mu _{0} \right )}{2}\frac{\partial }{\partial x}\left ( H_{x}^{2}+H_{y}^{2} \right ) \nonumber \]
La fuerza total es entonces
\ [\ begin {align} f_ {x} &=SD\ int_ {-\ infty} ^ {x_ {0}} F_ {x}\, dx\ nonumber\\ &
=\ frac {\ izquierda (\ mu -\ mu _ {0}\ derecha)} {2} sD\ izquierda (H_ {x} ^ {2} +H_ {y} ^ {2}\ derecha)\ bigg|_ {-\ infty} ^ {x_ {0}}\ nonumber\\ &
=\ frac {\ izquierda (\ mu -\ mu _ {0}\ derecha)} {2}\ frac {N^ {2} I^ {2} D} {s}\ end {align}\ nonumber\]
donde los campos at\(x=-\infty \) son cero y el campo at\(x=x_{0}\) viene dado por (12). El material de alta permeabilidad es atraído por regiones de campo magnético más fuerte. Es esta fuerza la que hace que los materiales de hierro sean atraídos hacia un imán. Los materiales diamagnéticos\(\left ( \mu < \mu _{0} \right )\) serán repelidos.
Este mismo resultado se puede obtener más fácilmente usando (6) donde el flujo a través del hueco es
\[\Phi =HD\left [ \mu x+\mu _{0}\left ( a-x \right ) \right ]=\frac{NID}{s}\left [ \left ( \mu -\mu _{0} \right )x+a\mu _{0} \right ] \nonumber \]
para que la inductancia sea
\[L=\frac{N\Phi }{I}=\frac{N^{2}D}{s}\left [ \left ( \mu -\mu _{0} \right )+a\mu _{0} \right ] \nonumber \]
Entonces la fuerza obtenida usando (6) concuerda con (15)
\[\begin{align} f_{x}&=\frac{1}{2}I^{2}\frac{dL\left (x \right )}{dx}\nonumber \\ &=\frac{\left ( \mu -\mu _{0} \right )}{2s}N^{2}I^{2}D\end{align} \nonumber \]


